Difference between revisions of "Complex Numbers"
Ramamurthy S (talk | contribs) |
Ramamurthy S (talk | contribs) |
||
| Line 2: | Line 2: | ||
== Definition == | == Definition == | ||
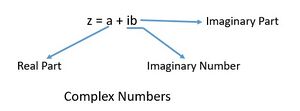
A complex number is the sum of a real number and an imaginary number. A complex number is of the form <math>a+ib</math> and is usually represented by <math>z</math>. | A complex number is the sum of a real number and an imaginary number. A complex number is of the form <math>a+ib</math> and is usually represented by <math>z</math>. <math>z=a+ib</math> | ||
<math>z | Here both <math>a</math> and <math>b</math> are real numbers. The value '<math>a</math>' is called the real part which is denoted by <math>Re \ z</math>, and '<math>b</math>' is called the imaginary part <math>Im\ z</math>. Also, <math>ib</math> is called an imaginary number. | ||
Examples of Complex Numbers : | Examples of Complex Numbers : | ||
| Line 20: | Line 20: | ||
For example: <math>z=2+i5</math> , then | For example: <math>z=2+i5</math> , then | ||
Real Part : <math>Re \ z = 2</math> | Real Part: <math>Re \ z = 2</math> | ||
Imaginary Part : <math>Im\ z = 5</math> | Imaginary Part: <math>Im\ z = 5</math> | ||
== Equality of complex numbers == | == Equality of complex numbers == | ||
| Line 43: | Line 43: | ||
<math>y=\frac{16+25}{5}=\frac{41}{5}</math> | <math>y=\frac{16+25}{5}=\frac{41}{5}</math> | ||
Answer : <math>x= \frac{4}{5}</math> and <math>y=\frac{41}{5}</math> | Answer: <math>x= \frac{4}{5}</math> and <math>y=\frac{41}{5}</math> | ||
Revision as of 18:20, 3 November 2023
Complex numbers are helpful in finding the square root of negative numbers. The concept of complex numbers was first referred to in the 1st century by a Greek mathematician, Hero of Alexandria when he tried to find the square root of a negative number. But he merely changed the negative into positive and simply took the numeric root value. Further, the real identity of a complex number was defined in the 16th century by Italian mathematician Gerolamo Cardano, in the process of finding the negative roots of cubic and quadratic polynomial expressions.
Definition
A complex number is the sum of a real number and an imaginary number. A complex number is of the form and is usually represented by .
Here both and are real numbers. The value '' is called the real part which is denoted by , and '' is called the imaginary part . Also, is called an imaginary number.
Examples of Complex Numbers :
Representation of a Complex Number
The way Complex Number is represented is shown in the fig.1.
For example: , then
Real Part:
Imaginary Part:
Equality of complex numbers
Two complex numbers and are equal if and
Example: if where x and y are real numbers, then find the values of x and y.
Equating the real and the imaginary parts of we get
Hence
Answer: and