The Modulus and the Conjugate of a Complex Number

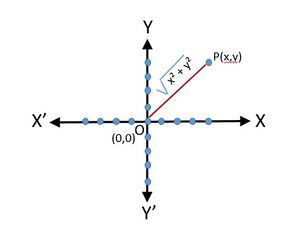
The modulus of a complex number gives the distance of the complex number from the origin in the Argand plane, whereas the conjugate of a complex number gives the reflection of the complex number about the real axis in the Argand plane.

Conjugate of a Complex Number

Fig 1 - Conjugate of a complex number

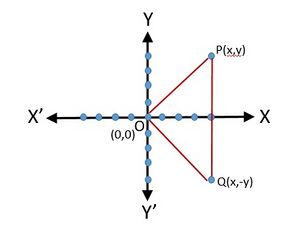
The representation of a complex number $z=x+iy$ and its conjugate ${\overline {zi}}=x-iy$ in the Argand plane are, respectively , the points $P(x,y)$ and $Q(x,y)$

Geometrically , the point $P(x,y)$ is the mirror image of the point $P(x,y)$ on the real axis (Fig 1)

Example: Find the conjugate of ${\frac {(3-2i)(2+3i)}{(1+2i)(2-i)}}$

${\frac {(3-2i)(2+3i)}{(1+2i)(2-i)}}$

$={\frac {(6+9i-4i-6i^{2})}{(2-i+4i-2i^{2})}}$ $={\frac {(6+5i-6(-1))}{(2+3i-2(-1))}}$

$={\frac {(6+5i+6)}{(2+3i+2)}}$$={\frac {(12+5i)}{(4+3i)}}$ $={\frac {(12+5i)}{(4+3i)}}\times {\frac {(4-3i)}{(4-3i)}}$

$={\frac {(48-36i+20i-15i^{2})}{(16-9i^{2})}}$$={\frac {(48-16i-15(-1))}{(16-9(-1))}}$$={\frac {63-16i}{25}}$$={\frac {63}{25}}-{\frac {16i}{25}}$

Answer: The conjugate of ${\frac {(3-2i)(2+3i)}{(1+2i)(2-i)}}$$={\frac {63}{25}}+{\frac {16i}{25}}$

Modulus of a Complex Number

Fig 2 - Modulus of a complex number