Difference between revisions of "मैक्सवेल-बोल्ट्ज़मैन आँकड़े"
| Line 1: | Line 1: | ||
{{distinguish| | {{distinguish|मैक्सवेल-बोल्ट्ज़मैन वितरण}} | ||
{{Short description|Statistical distribution used in many-particle mechanics}}{{Use American English|date=January 2019}}{{Statistical mechanics|cTopic=[[Particle statistics|Particle Statistics]]}} | {{Short description|Statistical distribution used in many-particle mechanics}}{{Use American English|date=January 2019}}{{Statistical mechanics|cTopic=[[Particle statistics|Particle Statistics]]}} | ||
[[Image:Maxwell-Boltzmann distribution 1.png|thumb|300px|मैक्सवेल-बोल्ट्ज़मैन आँकड़ों का उपयोग [[आदर्श गैस]] में कण गति के मैक्सवेल-बोल्ट्ज़मैन वितरण को प्राप्त करने के लिए किया जा सकता है। दिखाया गया: 10 के लिए कण गति का वितरण<sup>6</sup>ऑक्सीजन कण -100, 20 और 600°C पर।]][[सांख्यिकीय यांत्रिकी]] में, मैक्सवेल-बोल्ट्ज़मैन आँकड़े [[थर्मल संतुलन]] में विभिन्न ऊर्जा | [[Image:Maxwell-Boltzmann distribution 1.png|thumb|300px|मैक्सवेल-बोल्ट्ज़मैन आँकड़ों का उपयोग [[आदर्श गैस]] में कण गति के मैक्सवेल-बोल्ट्ज़मैन वितरण को प्राप्त करने के लिए किया जा सकता है। दिखाया गया: 10 के लिए कण गति का वितरण<sup>6</sup>ऑक्सीजन कण -100, 20 और 600°C पर।]][[सांख्यिकीय यांत्रिकी]] में, '''मैक्सवेल-बोल्ट्ज़मैन आँकड़े''' [[थर्मल संतुलन|ऊष्मीय संतुलन]] में विभिन्न ऊर्जा अवस्थाओं पर [[शास्त्रीय भौतिकी]] पदार्थ कणों के वितरण का वर्णन करते हैं। यह तब लागू होता है जब तापमान अत्यधिक अधिक होता है या कण घनत्व इतना कम होता है कि क्वांटम प्रभाव नगण्य हो जाता है। | ||
ऊर्जा | मैक्सवेल-बोल्ट्ज़मैन आँकड़ों के लिए ऊर्जा <math>\varepsilon_i</math> वाले कणों की अपेक्षित संख्या | ||
:<math>\langle N_i \rangle = \frac {g_i} {e^{(\varepsilon_i - \mu)/kT}} = \frac{N}{Z}\,g_i e^{-\varepsilon_i/kT},</math> | :<math>\langle N_i \rangle = \frac {g_i} {e^{(\varepsilon_i - \mu)/kT}} = \frac{N}{Z}\,g_i e^{-\varepsilon_i/kT},</math> | ||
है, जहां: | |||
*<math>\varepsilon_i</math> i-वें [[ऊर्जा]] स्तर की ऊर्जा है, | *<math>\varepsilon_i</math> i-वें [[ऊर्जा]] स्तर की ऊर्जा है, | ||
*<math>\langle N_i \rangle</math> ऊर्जा वाले | *<math>\langle N_i \rangle</math> <math>\varepsilon_i</math> ऊर्जा वाले अवस्थाओं के समुच्चय में कणों की औसत संख्या है , | ||
*<math>g_i</math> ऊर्जा स्तर i का अपक्षयी ऊर्जा स्तर है, अर्थात, ऊर्जा वाले | *<math>g_i</math> ऊर्जा स्तर i का अपक्षयी ऊर्जा स्तर है, अर्थात, ऊर्जा वाले अवस्थाओं की संख्या <math>\varepsilon_i</math> जिन्हें फिर भी किसी अन्य माध्यम से दूसरे से अलग किया जा सकता है,<ref group="nb">For example, two simple point particles may have the same energy, but different momentum vectors. They may be distinguished from each other on this basis, and the degeneracy will be the number of possible ways that they can be so distinguished.</ref> | ||
*μ [[रासायनिक क्षमता]] है, | *μ [[रासायनिक क्षमता]] है, | ||
*k बोल्ट्ज़मैन स्थिरांक है, | *k बोल्ट्ज़मैन स्थिरांक है, | ||
*T पूर्ण [[तापमान]] है, | *T पूर्ण [[तापमान]] है, | ||
* | *''N'' कणों की कुल संख्या है: <math display="block">N = \sum_i N_i,</math> | ||
*Z विभाजन फलन (सांख्यिकीय यांत्रिकी) है: <math display="block">Z = \sum_i g_i e^{-\varepsilon_i/kT},</math> | *Z विभाजन फलन (सांख्यिकीय यांत्रिकी) है: <math display="block">Z = \sum_i g_i e^{-\varepsilon_i/kT},</math> | ||
*e, E (गणितीय स्थिरांक) | *e, E (गणितीय स्थिरांक) या यूलर की संख्या है | ||
समान रूप से, कणों की संख्या को कभी-कभी | समान रूप से, कणों की संख्या को कभी-कभी | ||
:<math>\langle N_i \rangle = \frac {1} {e^{(\varepsilon_i - \mu)/kT}} = \frac{N}{Z}\,e^{-\varepsilon_i/kT},</math> | :<math>\langle N_i \rangle = \frac {1} {e^{(\varepsilon_i - \mu)/kT}} = \frac{N}{Z}\,e^{-\varepsilon_i/kT},</math> | ||
जहां सूचकांक अब ऊर्जा | के रूप में व्यक्त किया जाता है, जहां सूचकांक अब ऊर्जा <math>\varepsilon_i</math>, और <math display="inline">Z = \sum_i e^{-\varepsilon_i/kT}</math> वाले सभी अवस्थाओं के समुच्चय के अतिरिक्त एक विशेष अवस्था को निर्दिष्ट करता है। | ||
==इतिहास== | ==इतिहास== | ||
{{more| | {{more|मैक्सवेल-बोल्ट्ज़मैन वितरण}} | ||
मैक्सवेल-बोल्ट्ज़मैन आँकड़े मैक्सवेल-बोल्ट्ज़मैन वितरण से विकसित हुए, संभवतः अंतर्निहित तकनीक के आसवन के रूप | मैक्सवेल-बोल्ट्ज़मैन आँकड़े मैक्सवेल-बोल्ट्ज़मैन वितरण से विकसित हुए, संभवतः अंतर्निहित तकनीक के आसवन के रूप में है। वितरण प्रथतमतः मैक्सवेल द्वारा 1860 में अनुमान के आधार पर निकाला गया था। बोल्ट्ज़मैन ने बाद में, 1870 के दशक में, इस वितरण की भौतिक उत्पत्ति की महत्वपूर्ण जांच की थी। वितरण इस आधार पर प्राप्त किया जा सकता है कि यह निकाय की एन्ट्रापी को अधिकतम करता है। | ||
==प्रयोज्यता== | ==प्रयोज्यता== | ||
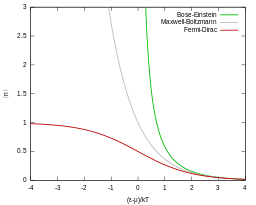
[[Image:Fermi-Dirac Bose-Einstein Maxwell-Boltzmann statistics.svg|256px|thumb|right|तीन आँकड़ों के लिए जमीनी स्थिति की औसत अधिभोग की तुलना]]मैक्सवेल-बोल्ट्ज़मैन सांख्यिकी का उपयोग किसी आदर्श गैस के मैक्सवेल-बोल्ट्ज़मैन वितरण को प्राप्त करने के लिए किया जाता है। | [[Image:Fermi-Dirac Bose-Einstein Maxwell-Boltzmann statistics.svg|256px|thumb|right|तीन आँकड़ों के लिए जमीनी स्थिति की औसत अधिभोग की तुलना]]मैक्सवेल-बोल्ट्ज़मैन सांख्यिकी का उपयोग किसी आदर्श गैस के मैक्सवेल-बोल्ट्ज़मैन वितरण को प्राप्त करने के लिए किया जाता है। यद्यपि, इसका उपयोग उस वितरण को भिन्न ऊर्जा-संवेग संबंध वाले कणों तक विस्तारित करने के लिए भी किया जा सकता है, जैसे कि सापेक्ष कण (जिसके परिणामस्वरूप मैक्सवेल-जुटनर वितरण होता है), और त्रि-आयामी स्थानों के अतिरिक्त अन्य। | ||
मैक्सवेल-बोल्ट्ज़मैन सांख्यिकी को | मैक्सवेल-बोल्ट्ज़मैन सांख्यिकी को प्रायः विशिष्ट शास्त्रीय कणों के आंकड़ों के रूप में वर्णित किया जाता है। दूसरे शब्दों में, अवस्था 1 में कण A और अवस्था 2 में कण B का विन्यास उस स्थिति से भिन्न है जिसमें कण B अवस्था 1 में है और कण A अवस्था 2 में है। यह धारणा उचित (बोल्ट्ज़मैन) आँकड़ों की ओर ले जाती है ऊर्जा अवस्थाओं में कण, परंतु एन्ट्रापी के लिए गैर-भौतिक परिणाम देते हैं, जैसा कि [[गिब्स विरोधाभास]] में सन्निहित है। | ||
साथ ही, ऐसे कोई वास्तविक कण नहीं हैं जिनमें मैक्सवेल-बोल्ट्ज़मैन सांख्यिकी के लिए आवश्यक विशेषताएं हों। | साथ ही, ऐसे कोई वास्तविक कण नहीं हैं जिनमें मैक्सवेल-बोल्ट्ज़मैन सांख्यिकी के लिए आवश्यक विशेषताएं हों। वस्तुतः, गिब्स विरोधाभास हल हो जाता है यदि हम निश्चित प्रकार के सभी कणों (जैसे, इलेक्ट्रॉन, प्रोटॉन, आदि) को मुख्य रूप से अप्रभेद्य मानते हैं। एक बार जब यह धारणा बन जाती है, तो कण आँकड़े बदल जाते हैं। मिश्रण उदाहरण की एन्ट्रापी में परिवर्तन को दो प्रकार के मिश्रित कणों की भिन्नता के परिणामस्वरूप होने वाली गैर-व्यापक एन्ट्रापी के उदाहरण के रूप में देखा जा सकता है। | ||
क्वांटम कण या तो बोसोन | क्वांटम कण या तो बोसोन (बोस-आइंस्टीन आंकड़ों के अनुसार) या फर्मियन ([[पाउली अपवर्जन सिद्धांत]] के अंतर्गत, इसके अतिरिक्त फर्मी-डिराक आंकड़ों) हैं। ये दोनों क्वांटम आँकड़े उच्च तापमान और कम कण घनत्व की सीमा में मैक्सवेल-बोल्ट्ज़मैन आँकड़ों के निकट पहुँचते हैं। | ||
== व्युत्पत्तियाँ == | == व्युत्पत्तियाँ == | ||
मैक्सवेल-बोल्ट्ज़मैन आँकड़े विभिन्न सांख्यिकीय यांत्रिकी | मैक्सवेल-बोल्ट्ज़मैन आँकड़े विभिन्न सांख्यिकीय यांत्रिकी ऊष्मागतिक समूहों में प्राप्त किए जा सकते हैं:<ref name="tolman">{{cite book | last=Tolman |first=R. C. | author-link = Richard C. Tolman | year=1938 | title=सांख्यिकीय यांत्रिकी के सिद्धांत| publisher=[[Dover Publications]] | isbn = 9780486638966}}</ref> | ||
* | * निश्चित भव्य [[विहित पहनावा|विहित समुच्चय]]। | ||
* विहित | * विहित समुच्चय, निश्चित। | ||
* [[माइक्रोकैनोनिकल पहनावा]], | * [[माइक्रोकैनोनिकल पहनावा|सूक्ष्मविहित समुच्चय]], परंतु मात्र ऊष्मागतिक सीमा में। | ||
प्रत्येक | प्रत्येक स्थिति में यह मानना आवश्यक है कि कण गैर-अंतःक्रिया कर रहे हैं, और कई कण ही स्थिति में रह सकते हैं और स्वतंत्र रूप से ऐसा कर सकते हैं। | ||
=== | === सूक्ष्मविहित समुच्चय से व्युत्पत्ति === | ||
मान लीजिए कि हमारे | मान लीजिए कि हमारे निकट पात्र है जिसमें समान भौतिक विशेषताओं (जैसे द्रव्यमान, आवेश, आदि) वाले बहुत छोटे कणों की बड़ी संख्या है। आइए इसे निकाय के रूप में देखें। मान लें कि यद्यपि कणों के गुण समान हैं, फिर भी वे भिन्न हैं। उदाहरण के लिए, हम प्रत्येक कण की पहचान उनके प्रक्षेपपथों को निरंतर देखकर, या प्रत्येक पर चिन्ह लगाकर कर सकते हैं, उदाहरण के लिए, प्रत्येक पर अलग संख्या खींचना, जैसा कि [[लॉटरी|प्रचयन]] गेंदों के साथ किया जाता है। | ||
कण उस | कण उस पात्र के भीतर सभी दिशाओं में बड़ी तीव्रता से घूम रहे हैं। क्योंकि कण तीव्रता से घूम रहे हैं, उनमें कुछ ऊर्जा होती है। मैक्सवेल-बोल्ट्ज़मैन वितरण गणितीय फलन है जो बताता है कि पात्र में कितने कणों में निश्चित ऊर्जा है। अधिक यथार्थ रूप से, मैक्सवेल-बोल्ट्ज़मान वितरण गैर-सामान्यीकृत संभाव्यता देता है (इसका अर्थ है कि संभावनाएं 1 तक नहीं जुड़ती हैं) कि विशेष ऊर्जा के अनुरूप अवस्था पर अधिकृत कर लिया गया है। | ||
सामान्यतः, समान मात्रा में ऊर्जा वाले कई कण हो सकते हैं <math>\varepsilon</math>. माना ऊर्जा वाले कणों की संख्या समान है <math>\varepsilon_1</math> होना <math>N_1</math>, अन्य ऊर्जा रखने वाले कणों की संख्या <math>\varepsilon_2</math> होना <math>N_2</math>, और सभी संभावित ऊर्जाओं के लिए आगे <math>\{ \varepsilon_i \mid i = 1, 2, 3, \ldots\}.</math> इस स्थिति का वर्णन करने के लिए, हम ऐसा कहते हैं <math>N_i</math> ऊर्जा स्तर की व्यवसाय संख्या है <math>i.</math> यदि हमें सभी व्यवसाय संख्याएँ ज्ञात हैं <math>\{N_i \mid i=1,2,3,\ldots\},</math> तब हमें निकाय की कुल ऊर्जा पता चलती है। यद्यपि, क्योंकि हम यह अंतर कर सकते हैं कि कौन से कण प्रत्येक ऊर्जा स्तर पर अधिकृत कर रहे हैं, व्यवसाय संख्याओं का समुच्चय <math> \{ N_i \mid i=1,2,3,\ldots\}</math> निकाय की स्थिति का पूरी तरह से वर्णन नहीं करता है। निकाय की स्थिति, या माइक्रोस्टेट का पूरी तरह से वर्णन करने के लिए, हमें यह निर्दिष्ट करना होगा कि प्रत्येक ऊर्जा स्तर में कौन से कण हैं। इस प्रकार जब हम निकाय के संभावित अवस्थाओं की संख्या की गणना करते हैं, तो हमें प्रत्येक माइक्रोस्टेट की गणना करनी चाहिए, न कि मात्रव्यवसाय संख्याओं के संभावित समुच्चयों की। | |||
आरंभ करने के लिए, मान लें कि प्रत्येक ऊर्जा स्तर पर | आरंभ करने के लिए, मान लें कि प्रत्येक ऊर्जा स्तर पर मात्रही अवस्था होती है <math>i</math> (कोई पतन नहीं है)। इसके बाद जो कुछ होता है वह कुछ संयुक्त सोच है जिसका कणों के भंडार का यथार्थ वर्णन करने में बहुत कम योगदान है। उदाहरण के लिए, मान लीजिए कि कुल है <math>k</math> बक्से लेबल किए गए <math>a,b,\ldots,k</math>. [[संयोजन]] की अवधारणा के साथ, हम गणना कर सकते हैं कि व्यवस्था करने के कितने तरीके हैं <math>N</math> बक्सों के समुच्चय में, जहाँ प्रत्येक बक्से के भीतर गेंदों के क्रम को ट्रैक नहीं किया जाता है। सबसे पहले, हम चयन करते हैं <math>N_a</math> कुल से गेंदें <math>N</math> बॉक्स में रखने के लिए गेंदें <math>a</math>, और शेष गेंदों में से प्रत्येक बॉक्स का चयन करना जारी रखें, यह सुनिश्चित करते हुए कि प्रत्येक गेंद किसी बॉक्स में रखी गई है। गेंदों को कितने तरीकों से व्यवस्थित किया जा सकता है? | ||
:<math> | :<math> | ||
| Line 66: | Line 66: | ||
यह सिर्फ [[बहुपद गुणांक]] है, एन वस्तुओं को के बक्से में व्यवस्थित करने के तरीकों की संख्या, एल-वें बॉक्स में एन रखा गया है<sub>l</sub>आइटम, प्रत्येक बॉक्स में आइटम के क्रमपरिवर्तन को अनदेखा कर रहे हैं। | यह सिर्फ [[बहुपद गुणांक]] है, एन वस्तुओं को के बक्से में व्यवस्थित करने के तरीकों की संख्या, एल-वें बॉक्स में एन रखा गया है<sub>l</sub>आइटम, प्रत्येक बॉक्स में आइटम के क्रमपरिवर्तन को अनदेखा कर रहे हैं। | ||
अब, उस | अब, उस स्थिति पर विचार करें जहां लगाने के से अधिक तरीके हैं <math> | ||
N_i | N_i | ||
</math> बॉक्स में कण <math> | </math> बॉक्स में कण <math> | ||
| Line 81: | Line 81: | ||
:<math>W=N!\prod_{i}\frac{g_i^{N_i}}{N_i!}</math> | :<math>W=N!\prod_{i}\frac{g_i^{N_i}}{N_i!}</math> | ||
यह W का वह रूप है जिसे सबसे पहले [[लुडविग बोल्ट्ज़मान]] ने व्युत्पन्न किया था। बोल्ट्ज़मैन का मौलिक समीकरण <math>S=k\,\ln W</math> | यह W का वह रूप है जिसे सबसे पहले [[लुडविग बोल्ट्ज़मान]] ने व्युत्पन्न किया था। बोल्ट्ज़मैन का मौलिक समीकरण <math>S=k\,\ln W</math> ऊष्मागतिक एन्ट्रॉपी एस को माइक्रोस्टेट्स डब्ल्यू की संख्या से संबंधित करता है, जहां के बोल्ट्जमैन स्थिरांक है। यद्यपि, [[जोशिया विलार्ड गिब्स]] द्वारा यह बताया गया था कि डब्ल्यू के लिए उपरोक्त अभिव्यक्ति [[व्यापक मात्रा]] में [[एन्ट्रापी]] उत्पन्न नहीं करती है, और इसलिए दोषपूर्ण है। इस समस्या को गिब्स विरोधाभास के नाम से जाना जाता है। समस्या यह है कि उपरोक्त समीकरण द्वारा माने गए कण [[समान कण]] नहीं हैं। दूसरे शब्दों में, दो ऊर्जा उपस्तरों में दो कणों (ए और बी) के लिए [ए, बी] द्वारा दर्शाई गई जनसंख्या को जनसंख्या [बी, ए] से अलग माना जाता है, जबकि अविभाज्य कणों के लिए, वे नहीं हैं। यदि हम अविभाज्य कणों के लिए तर्क को आगे बढ़ाते हैं, तो हमें बोस-आइंस्टीन सांख्यिकी | डब्ल्यू के लिए बोस-आइंस्टीन अभिव्यक्ति की ओर ले जाया जाता है: | ||
:<math>W=\prod_i \frac{(N_i+g_i-1)!}{N_i!(g_i-1)!}</math> | :<math>W=\prod_i \frac{(N_i+g_i-1)!}{N_i!(g_i-1)!}</math> | ||
| Line 95: | Line 95: | ||
यह मूलतः N द्वारा विभाजन है! डब्ल्यू के लिए बोल्ट्ज़मैन की मूल अभिव्यक्ति, और इस सुधार को 'के रूप में जाना जाता है{{visible anchor|correct Boltzmann counting}}. | यह मूलतः N द्वारा विभाजन है! डब्ल्यू के लिए बोल्ट्ज़मैन की मूल अभिव्यक्ति, और इस सुधार को 'के रूप में जाना जाता है{{visible anchor|correct Boltzmann counting}}. | ||
हम खोजना चाहते हैं <math>N_i</math> जिसके लिए समारोह <math>W</math> कणों की निश्चित संख्या होने की बाधा पर विचार करते हुए अधिकतम किया जाता है <math display="inline">\left(N=\sum N_i\right)</math> और निश्चित ऊर्जा <math display="inline">\left(E=\sum N_i \varepsilon_i\right)</math> | हम खोजना चाहते हैं <math>N_i</math> जिसके लिए समारोह <math>W</math> कणों की निश्चित संख्या होने की बाधा पर विचार करते हुए अधिकतम किया जाता है <math display="inline">\left(N=\sum N_i\right)</math> और निश्चित ऊर्जा <math display="inline">\left(E=\sum N_i \varepsilon_i\right)</math> पात्र में. की अधिकतम सीमा <math>W</math> और <math>\ln(W)</math> के समान मूल्यों द्वारा प्राप्त किये जाते हैं <math>N_i</math> और, चूंकि इसे गणितीय रूप से पूरा करना आसान है, हम इसके अतिरिक्त बाद वाले फलन को अधिकतम करेंगे। हम फलन बनाने वाले [[लैग्रेंज गुणक]] का उपयोग करके अपने समाधान को बाधित करते हैं: | ||
:<math>f(N_1,N_2,\ldots,N_n) = \textstyle \ln(W)+\alpha(N-\sum N_i) + \beta(E-\sum N_i \varepsilon_i)</math> | :<math>f(N_1,N_2,\ldots,N_n) = \textstyle \ln(W)+\alpha(N-\sum N_i) + \beta(E-\sum N_i \varepsilon_i)</math> | ||
| Line 114: | Line 114: | ||
:<math>E=\frac{\ln W}{\beta}-\frac{N}{\beta}-\frac{\alpha N}{\beta}</math> | :<math>E=\frac{\ln W}{\beta}-\frac{N}{\beta}-\frac{\alpha N}{\beta}</math> | ||
बोल्ट्ज़मैन ने महसूस किया कि यह | बोल्ट्ज़मैन ने महसूस किया कि यह ऊष्मागतिक समीकरणों#यूलर इंटीग्रल्स|थर्मोडायनामिक्स के यूलर-एकीकृत मौलिक समीकरण की अभिव्यक्ति मात्र है। ई को आंतरिक ऊर्जा के रूप में पहचानते हुए, यूलर-एकीकृत मौलिक समीकरण बताता है कि: | ||
:<math>E=TS-PV+\mu N</math> | :<math>E=TS-PV+\mu N</math> | ||
| Line 123: | Line 123: | ||
:<math>N_i = \frac{g_i}{e^{\varepsilon_i/kT}/z} </math> | :<math>N_i = \frac{g_i}{e^{\varepsilon_i/kT}/z} </math> | ||
जहां <math>z=\exp(\mu/kT)</math> पूर्ण [[गतिविधि (रसायन विज्ञान)]] है. | |||
वैकल्पिक रूप से, हम इस तथ्य का उपयोग कर सकते हैं | वैकल्पिक रूप से, हम इस तथ्य का उपयोग कर सकते हैं | ||
| Line 131: | Line 131: | ||
:<math>N_i = N\frac{g_i e^{-\varepsilon_i/kT}}{Z} </math> | :<math>N_i = N\frac{g_i e^{-\varepsilon_i/kT}}{Z} </math> | ||
जहां Z विभाजन | जहां Z विभाजन फलन (सांख्यिकीय यांत्रिकी) द्वारा परिभाषित है: | ||
:<math>Z = \sum_i g_i e^{-\varepsilon_i/kT}</math> | :<math>Z = \sum_i g_i e^{-\varepsilon_i/kT}</math> | ||
| Line 142: | Line 142: | ||
=== विहित पहनावे से व्युत्पत्ति === | === विहित पहनावे से व्युत्पत्ति === | ||
उपरोक्त चर्चा में, | उपरोक्त चर्चा में, निकाय की बहुलताओं का सीधे विश्लेषण करके बोल्ट्ज़मैन वितरण फलन प्राप्त किया गया था। वैकल्पिक रूप से, कोई विहित समुच्चय का उपयोग कर सकता है। विहित समूह में, प्रणाली जलाशय के साथ ऊष्मीय संपर्क में है। जबकि ऊर्जा प्रणाली और जलाशय के बीच प्रवाहित होने के लिए स्वतंत्र है, माना जाता है कि संयुक्त प्रणाली के लिए निरंतर तापमान, टी बनाए रखने के लिए जलाशय में असीम रूप से बड़ी ताप क्षमता होती है। | ||
वर्तमान संदर्भ में, हमारे | वर्तमान संदर्भ में, हमारे निकाय में ऊर्जा का स्तर माना जाता है <math>\varepsilon _i</math> पतनशीलता के साथ <math>g_i</math>. पहले की तरह, हम इस संभावना की गणना करना चाहेंगे कि हमारे निकाय में ऊर्जा है <math>\varepsilon_i</math>. | ||
अगर हमारा | अगर हमारा निकाय ठीक है <math>\; s_1</math>, तो जलाशय के लिए समान संख्या में माइक्रोस्टेट उपलब्ध होंगे। इस नंबर पर कॉल <math>\; \Omega _ R (s_1)</math>. धारणा के अनुसार, संयुक्त प्रणाली (जिस प्रणाली में हम रुचि रखते हैं और जलाशय) पृथक है, इसलिए सभी माइक्रोस्टेट समान रूप से संभावित हैं। इसलिए, उदाहरण के लिए, यदि <math> \; \Omega _ R (s_1) = 2 \; \Omega _ R (s_2) </math>, हम यह निष्कर्ष निकाल सकते हैं कि हमारा निकाय स्थिति में होने की संभावना दोगुनी है <math>\; s_1</math> अतिरिक्त <math>\; s_2</math>. सामान्यतः, यदि <math>\; P(s_i)</math> संभावना है कि हमारा निकाय स्थिति में है <math>\; s_i</math>, | ||
:<math>\frac{P(s_1)}{P(s_2)} = \frac{\Omega _ R (s_1)}{\Omega _ R (s_2)}.</math> | :<math>\frac{P(s_1)}{P(s_2)} = \frac{\Omega _ R (s_1)}{\Omega _ R (s_2)}.</math> | ||
| Line 152: | Line 152: | ||
:<math>\frac{P(s_1)}{P(s_2)} = \frac{ e^{S_R(s_1)/k} }{ e^{S_R(s_2)/k} } = e^{(S_R (s_1) - S_R (s_2))/k}.</math> | :<math>\frac{P(s_1)}{P(s_2)} = \frac{ e^{S_R(s_1)/k} }{ e^{S_R(s_2)/k} } = e^{(S_R (s_1) - S_R (s_2))/k}.</math> | ||
आगे हम | आगे हम ऊष्मागतिक पहचान को याद करते हैं (थर्मोडायनामिक्स के पहले नियम से): | ||
:<math>d S_R = \frac{1}{T} (d U_R + P \, d V_R - \mu \, d N_R).</math> | :<math>d S_R = \frac{1}{T} (d U_R + P \, d V_R - \mu \, d N_R).</math> | ||
| Line 158: | Line 158: | ||
:<math> S_R (s_1) - S_R (s_2) = \frac{1}{T} (U_R (s_1) - U_R (s_2)) = - \frac{1}{T} (E(s_1) - E(s_2)),</math> | :<math> S_R (s_1) - S_R (s_2) = \frac{1}{T} (U_R (s_1) - U_R (s_2)) = - \frac{1}{T} (E(s_1) - E(s_2)),</math> | ||
जहां <math> U_R (s_i) </math> और <math> E(s_i) </math> जलाशय और प्रणाली की ऊर्जाओं को निरूपित करें <math>s_i</math>, क्रमश। दूसरी समानता के लिए हमने ऊर्जा संरक्षण का प्रयोग किया है। संबंधित पहले समीकरण में प्रतिस्थापित करना <math>P(s_1), \; P(s_2)</math>: | |||
:<math> | :<math> | ||
\frac{P(s_1)}{P(s_2)} = \frac{ e^{ - E(s_1) / kT } }{ e^{ - E(s_2) / kT} }, | \frac{P(s_1)}{P(s_2)} = \frac{ e^{ - E(s_1) / kT } }{ e^{ - E(s_2) / kT} }, | ||
</math> | </math> | ||
जिसका अर्थ है, | जिसका अर्थ है, निकाय के किसी भी अवस्था के लिए | ||
:<math> | :<math> | ||
| Line 171: | Line 171: | ||
:<math> Z = \sum _s e^{- E(s) / kT}, </math> | :<math> Z = \sum _s e^{- E(s) / kT}, </math> | ||
जहां सूचकांक | जहां सूचकांक निकाय के सभी माइक्रोस्टेट्स से होकर गुजरता है। Z को कभी-कभी बोल्ट्ज़मैन 'सम ओवर स्टेट्स' (या मूल जर्मन में ज़ुस्टैंड्ससुमे) कहा जाता है। यदि हम सभी संभावित अवस्थाओं के अतिरिक्त ऊर्जा eigenvalues के माध्यम से योग को अनुक्रमित करते हैं, तो अध: पतन को ध्यान में रखा जाना चाहिए। हमारे निकाय में ऊर्जा होने की संभावना <math>\varepsilon _i</math> बस सभी संबंधित माइक्रोस्टेट्स की संभावनाओं का योग है: | ||
:<math>P (\varepsilon _i) = \frac{1}{Z} g_i e^{- \varepsilon_i / kT}</math> | :<math>P (\varepsilon _i) = \frac{1}{Z} g_i e^{- \varepsilon_i / kT}</math> | ||
| Line 180: | Line 180: | ||
इस व्युत्पत्ति पर टिप्पणियाँ: | इस व्युत्पत्ति पर टिप्पणियाँ: | ||
*ध्यान दें कि इस सूत्रीकरण में, प्रारंभिक धारणा... मान लीजिए कि | *ध्यान दें कि इस सूत्रीकरण में, प्रारंभिक धारणा... मान लीजिए कि निकाय में कुल एन कण हैं... को समाप्त कर दिया गया है। दरअसल, निकाय में मौजूद कणों की संख्या वितरण पर पहुंचने में कोई भूमिका नहीं निभाती है। बल्कि, कितने कण ऊर्जा वाले अवस्थाओं पर अधिकृत करेंगे <math>\varepsilon _i</math> आसान परिणाम के रूप में अनुसरण करता है। | ||
*ऊपर जो प्रस्तुत किया गया है वह मूलतः विहित विभाजन | *ऊपर जो प्रस्तुत किया गया है वह मूलतः विहित विभाजन फलन की व्युत्पत्ति है। जैसा कि कोई परिभाषाओं की तुलना करके देख सकता है, अवस्थाओं पर बोल्ट्ज़मैन का योग विहित विभाजन फलन के बराबर है। | ||
* | *निश्चित उसी दृष्टिकोण का उपयोग फर्मी-डिराक सांख्यिकी|फर्मी-डिराक और बोस-आइंस्टीन सांख्यिकी|बोस-आइंस्टीन सांख्यिकी प्राप्त करने के लिए किया जा सकता है। यद्यपि, वहाँ कोई विहित समुच्चय को भव्य विहित समुच्चय से बदल देगा, क्योंकि निकाय और जलाशय के बीच कणों का आदान-प्रदान होता है। साथ ही, उन मामलों में जिस प्रणाली पर विचार किया जाता है वह एकल कण अवस्था है, कण नहीं। (उपरोक्त चर्चा में, हम अपने निकाय को एकल परमाणु मान सकते थे।) | ||
==यह भी देखें== | ==यह भी देखें== | ||
Revision as of 18:29, 28 November 2023
| Statistical mechanics |
|---|
 |

सांख्यिकीय यांत्रिकी में, मैक्सवेल-बोल्ट्ज़मैन आँकड़े ऊष्मीय संतुलन में विभिन्न ऊर्जा अवस्थाओं पर शास्त्रीय भौतिकी पदार्थ कणों के वितरण का वर्णन करते हैं। यह तब लागू होता है जब तापमान अत्यधिक अधिक होता है या कण घनत्व इतना कम होता है कि क्वांटम प्रभाव नगण्य हो जाता है।
मैक्सवेल-बोल्ट्ज़मैन आँकड़ों के लिए ऊर्जा वाले कणों की अपेक्षित संख्या
है, जहां:
- i-वें ऊर्जा स्तर की ऊर्जा है,
- ऊर्जा वाले अवस्थाओं के समुच्चय में कणों की औसत संख्या है ,
- ऊर्जा स्तर i का अपक्षयी ऊर्जा स्तर है, अर्थात, ऊर्जा वाले अवस्थाओं की संख्या जिन्हें फिर भी किसी अन्य माध्यम से दूसरे से अलग किया जा सकता है,[nb 1]
- μ रासायनिक क्षमता है,
- k बोल्ट्ज़मैन स्थिरांक है,
- T पूर्ण तापमान है,
- N कणों की कुल संख्या है:
- Z विभाजन फलन (सांख्यिकीय यांत्रिकी) है:
- e, E (गणितीय स्थिरांक) या यूलर की संख्या है
समान रूप से, कणों की संख्या को कभी-कभी
के रूप में व्यक्त किया जाता है, जहां सूचकांक अब ऊर्जा , और वाले सभी अवस्थाओं के समुच्चय के अतिरिक्त एक विशेष अवस्था को निर्दिष्ट करता है।
इतिहास
मैक्सवेल-बोल्ट्ज़मैन आँकड़े मैक्सवेल-बोल्ट्ज़मैन वितरण से विकसित हुए, संभवतः अंतर्निहित तकनीक के आसवन के रूप में है। वितरण प्रथतमतः मैक्सवेल द्वारा 1860 में अनुमान के आधार पर निकाला गया था। बोल्ट्ज़मैन ने बाद में, 1870 के दशक में, इस वितरण की भौतिक उत्पत्ति की महत्वपूर्ण जांच की थी। वितरण इस आधार पर प्राप्त किया जा सकता है कि यह निकाय की एन्ट्रापी को अधिकतम करता है।
प्रयोज्यता
मैक्सवेल-बोल्ट्ज़मैन सांख्यिकी का उपयोग किसी आदर्श गैस के मैक्सवेल-बोल्ट्ज़मैन वितरण को प्राप्त करने के लिए किया जाता है। यद्यपि, इसका उपयोग उस वितरण को भिन्न ऊर्जा-संवेग संबंध वाले कणों तक विस्तारित करने के लिए भी किया जा सकता है, जैसे कि सापेक्ष कण (जिसके परिणामस्वरूप मैक्सवेल-जुटनर वितरण होता है), और त्रि-आयामी स्थानों के अतिरिक्त अन्य।
मैक्सवेल-बोल्ट्ज़मैन सांख्यिकी को प्रायः विशिष्ट शास्त्रीय कणों के आंकड़ों के रूप में वर्णित किया जाता है। दूसरे शब्दों में, अवस्था 1 में कण A और अवस्था 2 में कण B का विन्यास उस स्थिति से भिन्न है जिसमें कण B अवस्था 1 में है और कण A अवस्था 2 में है। यह धारणा उचित (बोल्ट्ज़मैन) आँकड़ों की ओर ले जाती है ऊर्जा अवस्थाओं में कण, परंतु एन्ट्रापी के लिए गैर-भौतिक परिणाम देते हैं, जैसा कि गिब्स विरोधाभास में सन्निहित है।
साथ ही, ऐसे कोई वास्तविक कण नहीं हैं जिनमें मैक्सवेल-बोल्ट्ज़मैन सांख्यिकी के लिए आवश्यक विशेषताएं हों। वस्तुतः, गिब्स विरोधाभास हल हो जाता है यदि हम निश्चित प्रकार के सभी कणों (जैसे, इलेक्ट्रॉन, प्रोटॉन, आदि) को मुख्य रूप से अप्रभेद्य मानते हैं। एक बार जब यह धारणा बन जाती है, तो कण आँकड़े बदल जाते हैं। मिश्रण उदाहरण की एन्ट्रापी में परिवर्तन को दो प्रकार के मिश्रित कणों की भिन्नता के परिणामस्वरूप होने वाली गैर-व्यापक एन्ट्रापी के उदाहरण के रूप में देखा जा सकता है।
क्वांटम कण या तो बोसोन (बोस-आइंस्टीन आंकड़ों के अनुसार) या फर्मियन (पाउली अपवर्जन सिद्धांत के अंतर्गत, इसके अतिरिक्त फर्मी-डिराक आंकड़ों) हैं। ये दोनों क्वांटम आँकड़े उच्च तापमान और कम कण घनत्व की सीमा में मैक्सवेल-बोल्ट्ज़मैन आँकड़ों के निकट पहुँचते हैं।
व्युत्पत्तियाँ
मैक्सवेल-बोल्ट्ज़मैन आँकड़े विभिन्न सांख्यिकीय यांत्रिकी ऊष्मागतिक समूहों में प्राप्त किए जा सकते हैं:[1]
- निश्चित भव्य विहित समुच्चय।
- विहित समुच्चय, निश्चित।
- सूक्ष्मविहित समुच्चय, परंतु मात्र ऊष्मागतिक सीमा में।
प्रत्येक स्थिति में यह मानना आवश्यक है कि कण गैर-अंतःक्रिया कर रहे हैं, और कई कण ही स्थिति में रह सकते हैं और स्वतंत्र रूप से ऐसा कर सकते हैं।
सूक्ष्मविहित समुच्चय से व्युत्पत्ति
मान लीजिए कि हमारे निकट पात्र है जिसमें समान भौतिक विशेषताओं (जैसे द्रव्यमान, आवेश, आदि) वाले बहुत छोटे कणों की बड़ी संख्या है। आइए इसे निकाय के रूप में देखें। मान लें कि यद्यपि कणों के गुण समान हैं, फिर भी वे भिन्न हैं। उदाहरण के लिए, हम प्रत्येक कण की पहचान उनके प्रक्षेपपथों को निरंतर देखकर, या प्रत्येक पर चिन्ह लगाकर कर सकते हैं, उदाहरण के लिए, प्रत्येक पर अलग संख्या खींचना, जैसा कि प्रचयन गेंदों के साथ किया जाता है।
कण उस पात्र के भीतर सभी दिशाओं में बड़ी तीव्रता से घूम रहे हैं। क्योंकि कण तीव्रता से घूम रहे हैं, उनमें कुछ ऊर्जा होती है। मैक्सवेल-बोल्ट्ज़मैन वितरण गणितीय फलन है जो बताता है कि पात्र में कितने कणों में निश्चित ऊर्जा है। अधिक यथार्थ रूप से, मैक्सवेल-बोल्ट्ज़मान वितरण गैर-सामान्यीकृत संभाव्यता देता है (इसका अर्थ है कि संभावनाएं 1 तक नहीं जुड़ती हैं) कि विशेष ऊर्जा के अनुरूप अवस्था पर अधिकृत कर लिया गया है।
सामान्यतः, समान मात्रा में ऊर्जा वाले कई कण हो सकते हैं . माना ऊर्जा वाले कणों की संख्या समान है होना , अन्य ऊर्जा रखने वाले कणों की संख्या होना , और सभी संभावित ऊर्जाओं के लिए आगे इस स्थिति का वर्णन करने के लिए, हम ऐसा कहते हैं ऊर्जा स्तर की व्यवसाय संख्या है यदि हमें सभी व्यवसाय संख्याएँ ज्ञात हैं तब हमें निकाय की कुल ऊर्जा पता चलती है। यद्यपि, क्योंकि हम यह अंतर कर सकते हैं कि कौन से कण प्रत्येक ऊर्जा स्तर पर अधिकृत कर रहे हैं, व्यवसाय संख्याओं का समुच्चय निकाय की स्थिति का पूरी तरह से वर्णन नहीं करता है। निकाय की स्थिति, या माइक्रोस्टेट का पूरी तरह से वर्णन करने के लिए, हमें यह निर्दिष्ट करना होगा कि प्रत्येक ऊर्जा स्तर में कौन से कण हैं। इस प्रकार जब हम निकाय के संभावित अवस्थाओं की संख्या की गणना करते हैं, तो हमें प्रत्येक माइक्रोस्टेट की गणना करनी चाहिए, न कि मात्रव्यवसाय संख्याओं के संभावित समुच्चयों की।
आरंभ करने के लिए, मान लें कि प्रत्येक ऊर्जा स्तर पर मात्रही अवस्था होती है (कोई पतन नहीं है)। इसके बाद जो कुछ होता है वह कुछ संयुक्त सोच है जिसका कणों के भंडार का यथार्थ वर्णन करने में बहुत कम योगदान है। उदाहरण के लिए, मान लीजिए कि कुल है बक्से लेबल किए गए . संयोजन की अवधारणा के साथ, हम गणना कर सकते हैं कि व्यवस्था करने के कितने तरीके हैं बक्सों के समुच्चय में, जहाँ प्रत्येक बक्से के भीतर गेंदों के क्रम को ट्रैक नहीं किया जाता है। सबसे पहले, हम चयन करते हैं कुल से गेंदें बॉक्स में रखने के लिए गेंदें , और शेष गेंदों में से प्रत्येक बॉक्स का चयन करना जारी रखें, यह सुनिश्चित करते हुए कि प्रत्येक गेंद किसी बॉक्स में रखी गई है। गेंदों को कितने तरीकों से व्यवस्थित किया जा सकता है?
चूँकि प्रत्येक गेंद को डिब्बे में रखा गया है, , और हम अभिव्यक्ति को इस प्रकार सरल बनाते हैं
यह सिर्फ बहुपद गुणांक है, एन वस्तुओं को के बक्से में व्यवस्थित करने के तरीकों की संख्या, एल-वें बॉक्स में एन रखा गया हैlआइटम, प्रत्येक बॉक्स में आइटम के क्रमपरिवर्तन को अनदेखा कर रहे हैं।
अब, उस स्थिति पर विचार करें जहां लगाने के से अधिक तरीके हैं बॉक्स में कण (अर्थात पतन की समस्या को ध्यान में रखते हुए)। यदि -वें बॉक्स में विकृति है , अर्थात यह है उप-बॉक्स ( समान ऊर्जा वाले बक्से . समान ऊर्जा वाली इन अवस्थाओं/बक्सों को पतित अवस्थाएँ कहा जाता है।), जैसे कि भरने का कोई भी तरीका -वें बॉक्स में जहां उप-बॉक्स में संख्या बदली जाती है, वह बॉक्स को भरने का अलग तरीका है, तो i-वें बॉक्स को भरने के तरीकों की संख्या को वितरित करने के तरीकों की संख्या से बढ़ाया जाना चाहिए वस्तुओं में उप-बॉक्स. रखने के तरीकों की संख्या में अलग पहचानी जाने वाली वस्तुएँ उप-बॉक्स है (पहली वस्तु इनमें से किसी में भी जा सकती है बक्सों में, दूसरी वस्तु भी इनमें से किसी में जा सकती है बक्से, और इसी तरह)। इस प्रकार तरीकों की संख्या वह कुल कणों को उनकी ऊर्जा के अनुसार ऊर्जा स्तरों में वर्गीकृत किया जा सकता है, जबकि प्रत्येक स्तर पर होना अलग-अलग स्थितियाँ ऐसी होती हैं कि i-वें स्तर समायोजित हो जाता है कण है:
यह W का वह रूप है जिसे सबसे पहले लुडविग बोल्ट्ज़मान ने व्युत्पन्न किया था। बोल्ट्ज़मैन का मौलिक समीकरण ऊष्मागतिक एन्ट्रॉपी एस को माइक्रोस्टेट्स डब्ल्यू की संख्या से संबंधित करता है, जहां के बोल्ट्जमैन स्थिरांक है। यद्यपि, जोशिया विलार्ड गिब्स द्वारा यह बताया गया था कि डब्ल्यू के लिए उपरोक्त अभिव्यक्ति व्यापक मात्रा में एन्ट्रापी उत्पन्न नहीं करती है, और इसलिए दोषपूर्ण है। इस समस्या को गिब्स विरोधाभास के नाम से जाना जाता है। समस्या यह है कि उपरोक्त समीकरण द्वारा माने गए कण समान कण नहीं हैं। दूसरे शब्दों में, दो ऊर्जा उपस्तरों में दो कणों (ए और बी) के लिए [ए, बी] द्वारा दर्शाई गई जनसंख्या को जनसंख्या [बी, ए] से अलग माना जाता है, जबकि अविभाज्य कणों के लिए, वे नहीं हैं। यदि हम अविभाज्य कणों के लिए तर्क को आगे बढ़ाते हैं, तो हमें बोस-आइंस्टीन सांख्यिकी | डब्ल्यू के लिए बोस-आइंस्टीन अभिव्यक्ति की ओर ले जाया जाता है:
मैक्सवेल-बोल्ट्ज़मैन वितरण पूर्ण शून्य से ऊपर के तापमान के लिए इस बोस-आइंस्टीन वितरण का अनुसरण करता है, जिसका अर्थ है कि . मैक्सवेल-बोल्ट्ज़मैन वितरण को भी कम घनत्व की आवश्यकता होती है, जिसका अर्थ है . इन शर्तों के तहत, हम फैक्टोरियल के लिए स्टर्लिंग सन्निकटन का उपयोग कर सकते हैं:
लिखना:
इस तथ्य का उपयोग करते हुए के लिए हम लिखने के लिए फिर से स्टर्लिंग के सन्निकटन का उपयोग कर सकते हैं:
यह मूलतः N द्वारा विभाजन है! डब्ल्यू के लिए बोल्ट्ज़मैन की मूल अभिव्यक्ति, और इस सुधार को 'के रूप में जाना जाता हैcorrect Boltzmann counting.
हम खोजना चाहते हैं जिसके लिए समारोह कणों की निश्चित संख्या होने की बाधा पर विचार करते हुए अधिकतम किया जाता है और निश्चित ऊर्जा पात्र में. की अधिकतम सीमा और के समान मूल्यों द्वारा प्राप्त किये जाते हैं और, चूंकि इसे गणितीय रूप से पूरा करना आसान है, हम इसके अतिरिक्त बाद वाले फलन को अधिकतम करेंगे। हम फलन बनाने वाले लैग्रेंज गुणक का उपयोग करके अपने समाधान को बाधित करते हैं:
अंत में
उपरोक्त अभिव्यक्ति को अधिकतम करने के लिए हम फ़र्मेट के प्रमेय (स्थिर बिंदु) को लागू करते हैं, जिसके अनुसार स्थानीय एक्स्ट्रेमा, यदि मौजूद है, तो महत्वपूर्ण बिंदुओं पर होना चाहिए (आंशिक व्युत्पन्न गायब हो जाते हैं):
उपरोक्त समीकरणों को हल करके () हम अभिव्यक्ति पर पहुंचते हैं :
इस अभिव्यक्ति को प्रतिस्थापित करते हुए के लिए समीकरण में और यह मानते हुए पैदावार:
या, पुनर्व्यवस्थित करना:
बोल्ट्ज़मैन ने महसूस किया कि यह ऊष्मागतिक समीकरणों#यूलर इंटीग्रल्स|थर्मोडायनामिक्स के यूलर-एकीकृत मौलिक समीकरण की अभिव्यक्ति मात्र है। ई को आंतरिक ऊर्जा के रूप में पहचानते हुए, यूलर-एकीकृत मौलिक समीकरण बताता है कि:
जहां T तापमान है, P दबाव है, V आयतन है, और μ रासायनिक क्षमता है। बोल्ट्ज़मैन का प्रसिद्ध समीकरण यह अहसास है कि एन्ट्रापी आनुपातिक है आनुपातिकता का स्थिरांक बोल्ट्ज़मैन स्थिरांक है। अवस्था के आदर्श गैस समीकरण (PV=NkT) का उपयोग करते हुए, यह तुरंत इसका अनुसरण करता है और ताकि आबादी अब लिखी जा सके:
ध्यान दें कि उपरोक्त सूत्र कभी-कभी लिखा जाता है:
जहां पूर्ण गतिविधि (रसायन विज्ञान) है.
वैकल्पिक रूप से, हम इस तथ्य का उपयोग कर सकते हैं
जनसंख्या संख्या प्राप्त करने के लिए
जहां Z विभाजन फलन (सांख्यिकीय यांत्रिकी) द्वारा परिभाषित है:
एक सन्निकटन में जहां εiइसे सतत चर माना जाता है, थॉमस-फर्मी सन्निकटन निरंतर अध:पतन जी उत्पन्न करता है जो आनुपातिक है ताकि:
जो ऊर्जा के लिए सिर्फ मैक्सवेल-बोल्ट्ज़मैन वितरण है।
विहित पहनावे से व्युत्पत्ति
उपरोक्त चर्चा में, निकाय की बहुलताओं का सीधे विश्लेषण करके बोल्ट्ज़मैन वितरण फलन प्राप्त किया गया था। वैकल्पिक रूप से, कोई विहित समुच्चय का उपयोग कर सकता है। विहित समूह में, प्रणाली जलाशय के साथ ऊष्मीय संपर्क में है। जबकि ऊर्जा प्रणाली और जलाशय के बीच प्रवाहित होने के लिए स्वतंत्र है, माना जाता है कि संयुक्त प्रणाली के लिए निरंतर तापमान, टी बनाए रखने के लिए जलाशय में असीम रूप से बड़ी ताप क्षमता होती है।
वर्तमान संदर्भ में, हमारे निकाय में ऊर्जा का स्तर माना जाता है पतनशीलता के साथ . पहले की तरह, हम इस संभावना की गणना करना चाहेंगे कि हमारे निकाय में ऊर्जा है .
अगर हमारा निकाय ठीक है , तो जलाशय के लिए समान संख्या में माइक्रोस्टेट उपलब्ध होंगे। इस नंबर पर कॉल . धारणा के अनुसार, संयुक्त प्रणाली (जिस प्रणाली में हम रुचि रखते हैं और जलाशय) पृथक है, इसलिए सभी माइक्रोस्टेट समान रूप से संभावित हैं। इसलिए, उदाहरण के लिए, यदि , हम यह निष्कर्ष निकाल सकते हैं कि हमारा निकाय स्थिति में होने की संभावना दोगुनी है अतिरिक्त . सामान्यतः, यदि संभावना है कि हमारा निकाय स्थिति में है ,
जलाशय की एन्ट्रापी के बाद से , उपरोक्त बन जाता है
आगे हम ऊष्मागतिक पहचान को याद करते हैं (थर्मोडायनामिक्स के पहले नियम से):
एक विहित समूह में, कणों का कोई आदान-प्रदान नहीं होता है, इसलिए पद शून्य है. इसी प्रकार, यह देता है
जहां और जलाशय और प्रणाली की ऊर्जाओं को निरूपित करें , क्रमश। दूसरी समानता के लिए हमने ऊर्जा संरक्षण का प्रयोग किया है। संबंधित पहले समीकरण में प्रतिस्थापित करना :
जिसका अर्थ है, निकाय के किसी भी अवस्था के लिए
जहां Z कुल संभाव्यता 1 बनाने के लिए उचित रूप से चुना गया स्थिरांक है। (Z स्थिरांक है बशर्ते कि तापमान T अपरिवर्तनीय हो।)
जहां सूचकांक निकाय के सभी माइक्रोस्टेट्स से होकर गुजरता है। Z को कभी-कभी बोल्ट्ज़मैन 'सम ओवर स्टेट्स' (या मूल जर्मन में ज़ुस्टैंड्ससुमे) कहा जाता है। यदि हम सभी संभावित अवस्थाओं के अतिरिक्त ऊर्जा eigenvalues के माध्यम से योग को अनुक्रमित करते हैं, तो अध: पतन को ध्यान में रखा जाना चाहिए। हमारे निकाय में ऊर्जा होने की संभावना बस सभी संबंधित माइक्रोस्टेट्स की संभावनाओं का योग है:
जहां, स्पष्ट संशोधन के साथ,
यह पहले जैसा ही परिणाम है।
इस व्युत्पत्ति पर टिप्पणियाँ:
- ध्यान दें कि इस सूत्रीकरण में, प्रारंभिक धारणा... मान लीजिए कि निकाय में कुल एन कण हैं... को समाप्त कर दिया गया है। दरअसल, निकाय में मौजूद कणों की संख्या वितरण पर पहुंचने में कोई भूमिका नहीं निभाती है। बल्कि, कितने कण ऊर्जा वाले अवस्थाओं पर अधिकृत करेंगे आसान परिणाम के रूप में अनुसरण करता है।
- ऊपर जो प्रस्तुत किया गया है वह मूलतः विहित विभाजन फलन की व्युत्पत्ति है। जैसा कि कोई परिभाषाओं की तुलना करके देख सकता है, अवस्थाओं पर बोल्ट्ज़मैन का योग विहित विभाजन फलन के बराबर है।
- निश्चित उसी दृष्टिकोण का उपयोग फर्मी-डिराक सांख्यिकी|फर्मी-डिराक और बोस-आइंस्टीन सांख्यिकी|बोस-आइंस्टीन सांख्यिकी प्राप्त करने के लिए किया जा सकता है। यद्यपि, वहाँ कोई विहित समुच्चय को भव्य विहित समुच्चय से बदल देगा, क्योंकि निकाय और जलाशय के बीच कणों का आदान-प्रदान होता है। साथ ही, उन मामलों में जिस प्रणाली पर विचार किया जाता है वह एकल कण अवस्था है, कण नहीं। (उपरोक्त चर्चा में, हम अपने निकाय को एकल परमाणु मान सकते थे।)
यह भी देखें
- बोस-आइंस्टीन आँकड़े
- फ़र्मी-डिराक आँकड़े
- बोल्ट्ज़मान कारक
टिप्पणियाँ
- ↑ For example, two simple point particles may have the same energy, but different momentum vectors. They may be distinguished from each other on this basis, and the degeneracy will be the number of possible ways that they can be so distinguished.
संदर्भ
- ↑ Tolman, R. C. (1938). सांख्यिकीय यांत्रिकी के सिद्धांत. Dover Publications. ISBN 9780486638966.
ग्रन्थसूची
- Carter, Ashley H., "Classical and Statistical Thermodynamics", Prentice–Hall, Inc., 2001, New Jersey.
- Raj Pathria, "Statistical Mechanics", Butterworth–Heinemann, 1996.