Difference between revisions of "Area of a Triangle - Determinants"
Ramamurthy S (talk | contribs) |
Ramamurthy S (talk | contribs) |
||
| Line 4: | Line 4: | ||
In this article, we will calculate the area of a triangle in determinant form using its formula. | In this article, we will calculate the area of a triangle in determinant form using its formula. | ||
== Area of a Triangle == | |||
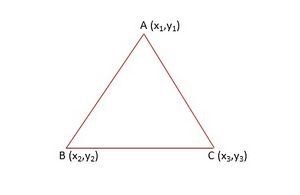
[[File:Triangle - Determinant.jpg|alt=Triangle - Determinant|thumb|Triangle - Determinant]] | |||
The area of triangle in determinant form can be evaluated if the vertices of the triangle are given. Consider the triangle <math>ABC</math> with vertices <math>A (x_1,y_1)</math>, <math>B (x_2,y_2)</math> , <math>C (x_3,y_3)</math> then its area can be calculated as | |||
<math>\frac{1}{2}\left[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\right ]</math> | |||
Revision as of 09:43, 30 January 2024
The area of triangle in determinant form is calculated in coordinate geometry when the coordinates of the vertices of the triangle are given. Finding the area of triangle in determinant form is one of the important applications of determinants.
The area of a triangle is half the product of the base and altitude of the triangle. But if the height of the triangle is unknown and its vertices are given, then we can find the area of the triangle using the determinant formula.
In this article, we will calculate the area of a triangle in determinant form using its formula.
Area of a Triangle
The area of triangle in determinant form can be evaluated if the vertices of the triangle are given. Consider the triangle with vertices , , then its area can be calculated as