Difference between revisions of "Real Numbers representation on the Number Line"
Ramamurthy S (talk | contribs) |
Ramamurthy S (talk | contribs) |
||
| Line 15: | Line 15: | ||
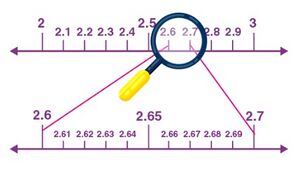
We know that point <math>2.665</math> lies on the number line between <math>2</math> and <math>3</math>. | We know that point <math>2.665</math> lies on the number line between <math>2</math> and <math>3</math>. | ||
[[File:Successive magnification - 1.jpg|alt=2 | [[File:Successive magnification - 1.jpg|alt=2 - 3|thumb|2 - 3|none]] | ||
In between 2 and 3, there are 10 equal parts, say 2.1, 2,2, 2.3, and so on. In order to locate the 2.665 exactly, again focus on the points between 2.6 and 2.7, as 2.665 is located in between. | In between 2 and 3, there are 10 equal parts, say 2.1, 2,2, 2.3, and so on. In order to locate the 2.665 exactly, again focus on the points between 2.6 and 2.7, as 2.665 is located in between. | ||
[[File:Successive magnification - 2.jpg|alt=2. | [[File:Successive magnification - 2.jpg|alt=2.6 - 2.7|thumb|2.6 - 2.7|none]] | ||
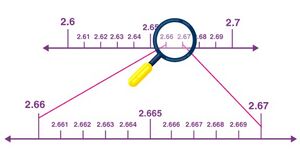
Since 2.665 is located between 2.66 and 2.67, again focus on these points. | Since 2.665 is located between 2.66 and 2.67, again focus on these points. | ||
[[File:Successive magnification - 3.jpg|alt=2. | [[File:Successive magnification - 3.jpg|alt=2.66 - 2.67|thumb|2.66 - 2.67|none]] | ||
Thus, point 2.665 is located on the number line using the process of successive magnification. So, with the help of this method, one can locate the point by a sufficient successive magnification process to visualize the representation of real numbers (rational and irrational numbers) on the number line. | Thus, point 2.665 is located on the number line using the process of successive magnification. So, with the help of this method, one can locate the point by a sufficient successive magnification process to visualize the representation of real numbers (rational and irrational numbers) on the number line. | ||
Latest revision as of 08:12, 7 May 2024
How to Represent the Real Numbers on the Number Line
Step 1: Draw a horizontal line with arrows on both sides. Mark the origin anywhere on the horizontal line.
Step 2: Mark the real numbers on the number line of equal lengths on both sides with a definite scale.
Step 3: Mark the positive numbers on the right side of the origin and negative numbers on the left side of the origin.
Step 4: If the given point is large, adjust the scale accordingly.
Step 5: If the given number is a rational or irrational number, convert them into a decimal format and mark the points using the process of successive magnification.
The process of visualization of numbers on the number line using the magnifying glass is called the process of successive magnification.
Let us try to locate the point on the number line.
We know that point lies on the number line between and .
In between 2 and 3, there are 10 equal parts, say 2.1, 2,2, 2.3, and so on. In order to locate the 2.665 exactly, again focus on the points between 2.6 and 2.7, as 2.665 is located in between.
Since 2.665 is located between 2.66 and 2.67, again focus on these points.
Thus, point 2.665 is located on the number line using the process of successive magnification. So, with the help of this method, one can locate the point by a sufficient successive magnification process to visualize the representation of real numbers (rational and irrational numbers) on the number line.