When we perform the operation of addition , multiplication on the pair of numbers , we will get another number. Similarly when we perform the operations on two sets , we will get another set. We will now define certain operations on sets and examine their properties.
Henceforth, we will refer all our sets as subsets of some universal set.
Union of sets
Let  and
and  be any two sets. Union of sets means taking all the elements of
be any two sets. Union of sets means taking all the elements of  and
and  keeping the common elements only once.
keeping the common elements only once. is the symbol to denote the union. Symbolically, we write
is the symbol to denote the union. Symbolically, we write  , it is read as "
, it is read as " union
union  ".
".
Example: 1
Let  and
and 
 . Here the common elements of these two sets are
. Here the common elements of these two sets are  which are taken only once while showing
which are taken only once while showing  ..
..
Example: 2
Let  and
and 
Here  is a subset of
is a subset of  . Union of sets
. Union of sets  and its subset
and its subset  is the set
is the set  itself.
itself.

i.e if  it is read as
it is read as  is a subset of
is a subset of  .
.
then 
Definition
The union of two sets  and
and  is the set
is the set  which consists of all those elements which are either in
which consists of all those elements which are either in  or in
or in  (including those which are in both). In symbols, we write
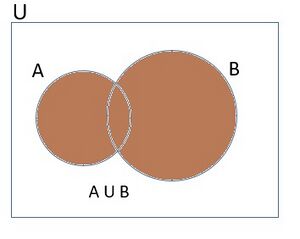
(including those which are in both). In symbols, we write  . The union of two sets can be represented by a Venn diagram as shown in Fig 1
. The union of two sets can be represented by a Venn diagram as shown in Fig 1
The shaded portion in Fig 1 represents  .
.
Intersection of sets
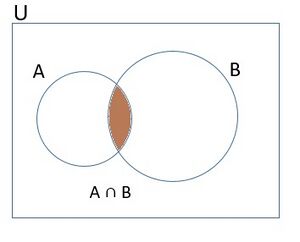
Fig 2 - Intersection of sets
If two sets  and
and  are given, then the intersection of
are given, then the intersection of  and
and  is the set of all elements which are common to both
is the set of all elements which are common to both  and
and  . Intersection is denoted by the symbol
. Intersection is denoted by the symbol  . Symbolically, we write
. Symbolically, we write  where
where  is the common element of both sets
is the common element of both sets  and
and  .
.
The intersection of two sets can be represented by a Venn diagram as shown in Fig 2.
Example:
Let  and
and 
Here  also
also  and
and  .
.
A pair of sets which does not have any common element are called disjoint sets.
For example, set  and
and  are disjoint sets as there are no
are disjoint sets as there are no
elements common between  and
and  .
.  meaning empty set.
meaning empty set.
This is represented by a Venn diagram as shown in Fig 3.
Difference of sets
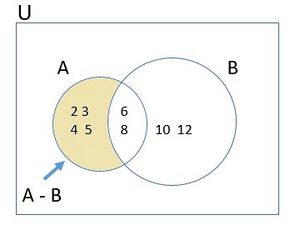
Fig 4 - Difference of sets
If there are two sets  and
and  , then the difference of two sets
, then the difference of two sets  and
and  is equal to the set which consists of elements present in
is equal to the set which consists of elements present in  but not in
but not in  . It is represented by
. It is represented by  read as
read as  minus
minus  .
.
Example: If  and
and  are two sets.
are two sets.
Then, the difference of set  and set
and set  is given by
is given by 
We can rewrite the definition of difference as 
The difference of two sets  and
and  can be represented by Venn diagram as shown in Fig 4. The shaded portion represents the difference of the two sets
can be represented by Venn diagram as shown in Fig 4. The shaded portion represents the difference of the two sets  and
and  .
.
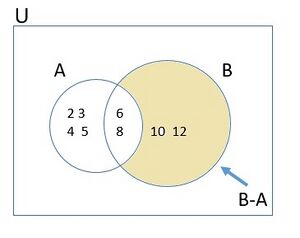
Fig 5 - Difference of sets
Then, the difference of set  and set
and set  is given by
is given by 
We can rewrite the definition of difference as 
The difference of two sets  and
and  can be represented by Venn diagram as
can be represented by Venn diagram as
shown in Fig 5. The shaded portion represents the difference of the two sets  and
and  .
.