क्रिस्टलोग्राफिक प्रतिबंध प्रमेय

अपने मूल रूप में क्रिस्टलोग्राफिक प्रतिबंध प्रमेय इस अवलोकन पर आधारित था कि क्रिस्टल की घूर्णी समरूपता आमतौर पर 2-गुना, 3-गुना, 4-गुना और 6-गुना तक सीमित होती है। हालाँकि, क्वासिक क्रिस्टल अन्य विवर्तन पैटर्न समरूपता के साथ हो सकते हैं, जैसे 5-गुना; इन्हें 1982 तक और शेख्टमैन द्वारा खोजा नहीं गया था। क्रिस्टल को असतत जाली (समूह) के रूप में तैयार किया जाता है, जो रैखिक स्वतंत्रता परिमित अनुवादों की सूची द्वारा उत्पन्न होता है (Coxeter 1989). क्योंकि असततता के लिए आवश्यक है कि जाली बिंदुओं के बीच की दूरी कम हो, किसी भी बिंदु पर जाली के घूर्णी समरूपता के समूह (गणित) को एक परिमित समूह होना चाहिए (वैकल्पिक रूप से, बिंदु एकमात्र प्रणाली है जो अनंत घूर्णी समरूपता की अनुमति देता है)। प्रमेय की ताकत यह है कि सभी परिमित समूह असतत जाली के साथ संगत नहीं होते हैं; किसी भी आयाम में, हमारे पास संगत समूहों की सीमित संख्या होगी।

आयाम 2 और 3

2D (वॉलपेपर समूह) और 3D (अंतरिक्ष समूह) के विशेष मामले अनुप्रयोगों में सबसे अधिक उपयोग किए जाते हैं, और उनका एक साथ इलाज किया जा सकता है।

जाली सबूत

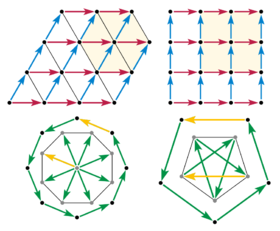
आयाम 2 या 3 में एक रोटेशन समरूपता को समूह क्रिया (गणित) में एक जाली बिंदु को स्थानांतरित करना चाहिए # एक ही विमान में अन्य जाली बिंदुओं के ऑर्बिट और स्टेबलाइजर्स, समतलीय जाली बिंदुओं के एक नियमित बहुभुज का निर्माण करते हैं। अब हम अपना ध्यान उस तल तक सीमित रखते हैं जिसमें सममिति कार्य करती है (Scherrer 1946), आकृति में जाली वेक्टर (ज्यामितीय) के साथ सचित्र।

जाली बहुभुजों को प्रतिबंधित करती हैं
संगत: 6-गुना (3-गुना), 4-गुना (2-गुना)
असंगत: 8 गुना, 5 गुना

अब एक 8-गुना घुमाव और बहुभुज के आसन्न बिंदुओं के बीच विस्थापन सदिशों पर विचार करें। यदि किन्हीं दो जालक बिन्दुओं के बीच विस्थापन होता है, तो जालक में हर जगह वही विस्थापन दोहराया जाता है। तो एक जाली बिंदु पर शुरू करने के लिए सभी किनारों के विस्थापन को इकट्ठा करें। किनारे के वैक्टर रेडियल वैक्टर बन जाते हैं, और उनकी 8 गुना समरूपता संग्रह बिंदु के चारों ओर जाली बिंदुओं के नियमित अष्टकोना का अर्थ है। लेकिन यह असंभव है, क्योंकि नया अष्टकोना मूल रूप से लगभग 80% बड़ा है। सिकुड़ने का महत्व यह है कि यह असीमित है। उसी निर्माण को नए अष्टकोण के साथ दोहराया जा सकता है, और बार-बार जाली बिंदुओं के बीच की दूरी जितनी छोटी हो उतनी छोटी होती है; इस प्रकार किसी असतत जाली में 8 गुना समरूपता नहीं हो सकती। 6 से अधिक k के लिए, किसी भी k-fold रोटेशन पर समान तर्क लागू होता है।

एक सिकुड़ता हुआ तर्क 5-गुना समरूपता को भी समाप्त कर देता है। जाली बिंदुओं के एक नियमित पेंटागन पर विचार करें। यदि यह मौजूद है, तो हम हर दूसरे किनारे के विस्थापन को ले सकते हैं और (सिर से पूंछ तक) 5-पॉइंट स्टार को इकट्ठा कर सकते हैं, जिसमें अंतिम किनारा शुरुआती बिंदु पर लौटता है। ऐसे तारे के शीर्ष फिर से 5 गुना समरूपता वाले एक नियमित पंचकोण के शीर्ष हैं, लेकिन मूल से लगभग 60% छोटे हैं।

इस प्रकार प्रमेय सिद्ध होता है।

क्वैसिक्रिस्टल और पेनरोज़ टाइलिंग के अस्तित्व से पता चलता है कि एक रेखीय अनुवाद की धारणा आवश्यक है। पेनरोज़ टिलिंग्स में 5 गुना घूर्णी समरूपता और एक असतत जाली हो सकती है, और टाइलिंग के किसी भी स्थानीय पड़ोस को कई बार असीम रूप से दोहराया जाता है, लेकिन समग्र रूप से टाइलिंग के लिए कोई रैखिक अनुवाद नहीं होता है। और असतत जाली धारणा के बिना, उपरोक्त निर्माण न केवल एक विरोधाभास तक पहुंचने में विफल रहता है, बल्कि एक (गैर-असतत) प्रति उदाहरण पैदा करता है। इस प्रकार 5-गुना घूर्णी समरूपता को एक ऐसे तर्क द्वारा समाप्त नहीं किया जा सकता है जो उन धारणाओं में से किसी एक को खो देता है। पूरे (अनंत) तल की एक पेनरोज़ टाइलिंग में केवल एक बिंदु के बारे में सटीक 5-गुना घूर्णी समरूपता (संपूर्ण टाइलिंग की) हो सकती है, जबकि 4-गुना और 6-गुना जाली में घूर्णी समरूपता के असीम रूप से कई केंद्र होते हैं।

त्रिकोणमिति प्रमाण

अनुवाद सदिश r द्वारा अलग किए गए दो जाली बिंदुओं A और B पर विचार करें। एक कोण α पर विचार करें जैसे कि किसी जाली बिंदु के बारे में कोण α का घूर्णन जाली का समरूपता है। α मानचित्रों द्वारा बिंदु B के बारे में घूमना A को एक नए बिंदु A' पर इंगित करता है। इसी तरह, α द्वारा बिंदु A के बारे में घूमना B को बिंदु B' पर मैप करता है। चूँकि उल्लिखित दोनों घुमाव समरूपता संक्रियाएँ हैं, A' और B' दोनों ही जाली बिंदु होने चाहिए। क्रिस्टल की आवधिकता के कारण, नया वेक्टर आर जो उन्हें जोड़ता है, आर के एक पूर्णांक बहु के बराबर होना चाहिए:

$\mathbf {r} '=m\mathbf {r}$

साथ $m$ पूर्णांक। चार अनुवाद वैक्टर, लंबाई के तीन $r=|\mathbf {r} |$ और एक, लंबाई के A' और B' को जोड़ने वाला $r'=|\mathbf {r} '|$, एक ट्रेपेज़ियम बनाएं। इसलिए, 'r' की लंबाई भी इसके द्वारा दी गई है:

$r'=2r\cos \alpha -r.$

दो समीकरणों का संयोजन देता है:

$\cos \alpha ={\frac {m+1}{2}}={\frac {M}{2}}$

कहाँ $M=m+1$ एक पूर्णांक भी है। इसे ध्यान में रखते हुए $|\cos \alpha |\leq 1$ हमने पूर्णांकों की अनुमति दी है $M\in \{-2,-1,0,1,2\}$. के संभावित मानों को हल करना $\alpha$ पता चलता है कि 0° से 180° श्रेणी में केवल 0°, 60°, 90°, 120°, और 180° हैं। रेडियंस में, जाली आवधिकता के अनुरूप केवल अनुमत घुमाव 2π/n द्वारा दिए जाते हैं, जहां n = 1, 2, 3, 4, 6. यह 1-, 2-, 3-, 4- और 6-गुना से मेल खाता है समरूपता, क्रमशः, और इसलिए 5 गुना या 6 गुना से अधिक समरूपता की संभावना को बाहर करता है।

लघु त्रिकोणमिति प्रमाण

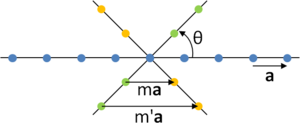
दूरी ए से अलग ए-ओ-बी परमाणुओं की एक रेखा पर विचार करें। पूरी पंक्ति को θ = +2π/n और θ = -2π/n द्वारा घुमाएँ, बिंदु O को स्थिर रखते हुए। +2π/n द्वारा घूर्णन के बाद, A को जाली बिंदु C पर ले जाया जाता है और -2π/n द्वारा घूर्णन के बाद, B को जाली बिंदु D पर ले जाया जाता है। जाली की अनुमानित आवधिकता के कारण, दो जाली बिंदु C और D भी प्रारंभिक पंक्ति के ठीक नीचे एक पंक्ति में होगा; इसके अलावा C और D को r = ma द्वारा अलग किया जाएगा, m एक पूर्णांक के साथ। लेकिन त्रिकोणमिति द्वारा, इन बिंदुओं के बीच अलगाव है:

$2a\cos {\theta }=2a\cos {\frac {2\pi }{n}}$.

दो संबंधों को बराबर करना देता है:

$2\cos {\frac {2\pi }{n}}=m$

यह केवल n = 1, 2, 3, 4, 6 से संतुष्ट होता है।

मैट्रिक्स प्रमाण

वैकल्पिक सबूत के लिए, मैट्रिक्स (गणित) गुणों पर विचार करें। मैट्रिक्स के विकर्ण तत्वों के योग को मैट्रिक्स का ट्रेस (मैट्रिक्स) कहा जाता है। 2डी और 3डी में प्रत्येक घूर्णन एक तलीय घूर्णन है, और ट्रेस अकेले कोण का एक कार्य है। 2डी रोटेशन के लिए ट्रेस 2 cos θ है; 3डी रोटेशन के लिए, 1 + 2 cos θ।

उदाहरण

• 2डी में ऑर्थोनॉर्मल आधार के संबंध में 60° (6 गुना) रोटेशन मैट्रिक्स पर विचार करें।

${\begin{bmatrix}{1/2}&-{{\sqrt {3}}/2}\\{{\sqrt {3}}/2}&{1/2}\end{bmatrix}}$

ट्रेस ठीक 1, एक पूर्णांक है।

• 45° (8-गुना) रोटेशन मैट्रिक्स पर विचार करें।

${\begin{bmatrix}{1/{\sqrt {2}}}&-{1/{\sqrt {2}}}\\{1/{\sqrt {2}}}&{1/{\sqrt {2}}}\end{bmatrix}}$

ट्रेस 2 / है√2, पूर्णांक नहीं।

सदिशों से बने एक आधार का चयन करना जो जालक को फैलाता है, न तो ऑर्थोगोनलिटी और न ही इकाई लंबाई की गारंटी है, केवल रैखिक स्वतंत्रता। हालाँकि रोटेशन मैट्रिक्स का ट्रेस किसी भी आधार के संबंध में समान है। ट्रेस रैखिक परिवर्तनों के तहत एक समानता का व्युत्क्रम है। जाली के आधार पर, रोटेशन ऑपरेशन को प्रत्येक जाली बिंदु को जाली वैक्टरों की एक पूर्णांक संख्या में मैप करना चाहिए, इसलिए जाली आधार में रोटेशन मैट्रिक्स की प्रविष्टियां - और इसलिए ट्रेस - अनिवार्य रूप से पूर्णांक हैं। अन्य सबूतों के समान, इसका तात्पर्य है कि केवल अनुमत घूर्णी समरूपता 1,2,3,4 या 6-गुना आक्रमण के अनुरूप है। उदाहरण के लिए, वॉलपेपर और क्रिस्टल को 45° से नहीं घुमाया जा सकता है और वे अपरिवर्तित रहते हैं, केवल संभव कोण हैं: 360°, 180°, 120°, 90° या 60°।

उदाहरण

• एक 60° (360°/6) रोटेशन मैट्रिक्स पर विचार करें :wikt:ओब्लिक जाली आधार के संबंध में समबाहु त्रिभुजों द्वारा चौकोर के लिए।

${\begin{bmatrix}0&-1\\1&1\end{bmatrix}}$

ट्रेस अभी भी 1 है। निर्धारक (रोटेशन के लिए हमेशा +1) भी संरक्षित है।

रोटेशन पर सामान्य क्रिस्टलोग्राफिक प्रतिबंध यह गारंटी नहीं देता है कि रोटेशन एक विशिष्ट जाली के साथ संगत होगा। उदाहरण के लिए, एक वर्गाकार जालक के साथ 60° का घुमाव काम नहीं करेगा; न ही एक आयताकार जालक के साथ 90° का घूर्णन कार्य करेगा।

उच्च आयाम

जब जाली का आयाम चार या अधिक तक बढ़ जाता है, तो घुमावों को समतल होने की आवश्यकता नहीं होती है; 2D प्रमाण अपर्याप्त है। हालाँकि, प्रतिबंध अभी भी लागू होते हैं, हालाँकि अधिक समरूपता की अनुमति है। उदाहरण के लिए, [[अतिविम िक जाली]] में आठ गुना घूर्णी समरूपता होती है, जो हाइपरक्यूब की आठ गुना घूर्णी समरूपता के अनुरूप होती है। यह केवल गणित के लिए ही नहीं, बल्कि एपेरियोडिक टाइलिंग#कट-एंड-प्रोजेक्ट विधि|कट-एंड-प्रोजेक्ट थ्योरी के तहत क्वासिक क्रिस्टल के भौतिकी के लिए रुचिकर है। इस दृष्टि से, 8-गुना घूर्णन समरूपता के साथ एक 3डी क्वैसिक्रिस्टल को 4डी जाली से कटे हुए स्लैब के प्रक्षेपण के रूप में वर्णित किया जा सकता है।

निम्नलिखित 4D रोटेशन मैट्रिक्स हाइपरक्यूब (और क्रॉस-पॉलीटॉप) की उपरोक्त आठ गुना समरूपता है:

$A={\begin{bmatrix}0&0&0&-1\\1&0&0&0\\0&-1&0&0\\0&0&-1&0\end{bmatrix}}.$

इस मैट्रिक्स को द्वारा दिए गए नए निर्देशांक में बदलना

$B={\begin{bmatrix}-1/2&0&-1/2&{\sqrt {2}}/2\\1/2&{\sqrt {2}}/2&-1/2&0\\-1/2&0&-1/2&-{\sqrt {2}}/2\\-1/2&{\sqrt {2}}/2&1/2&0\end{bmatrix}}$ उत्पादन करेंगे:

$BAB^{-1}={\begin{bmatrix}{\sqrt {2}}/2&{\sqrt {2}}/2&0&0\\-{\sqrt {2}}/2&{\sqrt {2}}/2&0&0\\0&0&-{\sqrt {2}}/2&{\sqrt {2}}/2\\0&0&-{\sqrt {2}}/2&-{\sqrt {2}}/2\end{bmatrix}}.$

यह तीसरा मैट्रिक्स तब 45 ° (पहले दो आयामों में) और 135 ° (अंतिम दो में) दोनों के रोटेशन से मेल खाता है। नए निर्देशांकों के पहले दो आयामों के साथ हाइपरक्यूब्स के एक स्लैब को पेश करने से एक अम्मान-बीनकर टाइलिंग (पिछले दो आयामों के साथ प्रोजेक्ट करके एक और ऐसी टाइलिंग का उत्पादन किया जाता है) उत्पन्न होता है, इसलिए इसमें औसतन 8 गुना घूर्णी समरूपता भी होती है।

A4 जाली और F4 जाली में क्रमशः 10 क्रम और 12 घूर्णी समरूपताएँ हैं।

सभी आयामों के लिए प्रतिबंध को बताने के लिए, केवल घुमावों से ध्यान हटाना और पूर्णांक मैट्रिसेस पर ध्यान केंद्रित करना सुविधाजनक है (Bamberg, Cairns & Kilminster 2003). हम कहते हैं कि एक मैट्रिक्स A में ऑर्डर (समूह सिद्धांत) k है जब इसकी k-th शक्ति (लेकिन कम नहीं), A^k, सर्वसमिका के बराबर है। इस प्रकार समबाहु त्रिभुज आधार में 6 गुना रोटेशन मैट्रिक्स क्रम 6 के साथ एक पूर्णांक मैट्रिक्स है। चलो ऑर्ड_N पूर्णांकों के सेट को निरूपित करें जो एक N × N पूर्णांक मैट्रिक्स का क्रम हो सकता है। उदाहरण के लिए, ऑर्ड₂ = {1, 2, 3, 4, 6}। हम ऑर्ड के लिए एक स्पष्ट सूत्र बताना चाहते हैं_N.

यूलर के पूर्ण फलन φ पर आधारित एक फलन ψ परिभाषित करें; यह सकारात्मक पूर्णांकों को गैर-ऋणात्मक पूर्णांकों में मैप करेगा। एक विषम अभाज्य संख्या, p और एक धनात्मक पूर्णांक k के लिए, ψ(p^k) कुल फ़ंक्शन मान के बराबर, φ (पी^k), जो इस मामले में p है^{के</सुप>−पीके−1</सुप>. ψ(2) के लिए भी ऐसा ही करेंk) जब k > 1. ψ(2) और ψ(1) को 0 पर सेट करें। अंकगणित के मौलिक प्रमेय का उपयोग करके, हम प्रमुख शक्तियों के उत्पाद के रूप में अद्वितीय रूप से कोई अन्य सकारात्मक पूर्णांक लिख सकते हैं, m = Π_α p_α<विस्तार>k _α? सेट ψ(एम) = Σ_α ψ(पृ_α<अवधि>के _α). यह कुल से भिन्न है, क्योंकि यह गुणनफल के स्थान पर योग है।}

सामान्य रूप में क्रिस्टलोग्राफिक प्रतिबंध बताता है कि ऑर्ड_N उन धनात्मक पूर्णांकों m से मिलकर बनता है जैसे कि ψ(m) ≤ N।

Smallest dimension for a given orderOEIS: A080737

m	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
ψ(m)	0	0	2	2	4	2	6	4	6	4	10	4	12	6	6	8	16	6	18	6	8	10	22	6	20	12	18	8	28	6	30

m>2 के लिए, ψ(m) के मान बीजगणितीय संख्या#गुण cos(2π/m) के दोगुने के बराबर हैं; इसलिए, ψ(m) m से सख्ती से कम है और इस अधिकतम मूल्य तक पहुँचता है यदि और केवल यदि m एक अभाज्य संख्या है।

ये अतिरिक्त समरूपताएं एक प्लानर स्लाइस को 8-गुना रोटेशन समरूपता की अनुमति नहीं देती हैं। विमान में, 2डी प्रतिबंध अभी भी लागू होते हैं। इस प्रकार क्वासिक्रिस्टल को मॉडल करने के लिए उपयोग किए जाने वाले कटों में आवश्यक रूप से मोटाई होती है।

पूर्णांक मैट्रिसेस घुमावों तक सीमित नहीं हैं; उदाहरण के लिए, एक प्रतिबिंब भी क्रम 2 की समरूपता है। लेकिन निर्धारक +1 पर जोर देकर, हम आव्यूहों को उचित घूर्णन तक सीमित कर सकते हैं।

आइसोमेट्री के संदर्भ में सूत्रीकरण

यूक्लिडियन अंतरिक्ष की आइसोमेट्री के संदर्भ में क्रिस्टलोग्राफिक प्रतिबंध प्रमेय तैयार किया जा सकता है। आइसोमेट्री का एक सेट एक समूह (गणित) बना सकता है। असतत आइसोमेट्री समूह से हमारा तात्पर्य एक आइसोमेट्री समूह से होगा जो प्रत्येक बिंदु को 'आर' के असतत उपसमुच्चय के लिए मैप करता है।^N, यानी समूह क्रिया (गणित)#किसी भी बिंदु की कक्षाएँ और स्टेबलाइजर्स अलग-अलग बिंदुओं का एक समूह है। इस शब्दावली के साथ, दो और तीन आयामों में क्रिस्टलोग्राफिक प्रतिबंध प्रमेय निम्नानुसार तैयार किया जा सकता है।

दो और तीन आयामी अंतरिक्ष में प्रत्येक असतत आइसोमेट्री समूह के लिए जिसमें पूरे अंतरिक्ष में फैले अनुवाद शामिल हैं, परिमित क्रम (समूह सिद्धांत) के सभी आइसोमेट्री क्रम 1, 2, 3, 4 या 6 के हैं।

ऑर्डर एन के आइसोमेट्रीज़ में शामिल हैं, लेकिन एन-फोल्ड रोटेशन तक सीमित नहीं हैं। प्रमेय भी S को बाहर करता है₈, एस₁₂, डी_4d, और डी_6d(तीन आयामों में बिंदु समूह देखें), भले ही उनके पास केवल 4- और 6-गुना घूर्णी समरूपता हो। एक अक्ष के बारे में किसी भी क्रम की घूर्णी समरूपता उस अक्ष के साथ अनुवाद संबंधी समरूपता के साथ संगत है।

उपरोक्त तालिका में परिणाम का अर्थ है कि चार और पांच-आयामी अंतरिक्ष में प्रत्येक असतत आइसोमेट्री समूह के लिए जिसमें संपूर्ण स्थान में फैले अनुवाद शामिल हैं, परिमित क्रम के सभी आइसोमेट्री क्रम 1, 2, 3, 4, 5, 6, 8 के हैं। , 10, या 12।

छह और सात-आयामी अंतरिक्ष में परिमित क्रम के सभी आइसोमेट्री क्रम 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 18, 20, 24 या 30 के हैं।

यह भी देखें

• क्रिस्टलोग्राफिक बिंदु समूह
• क्रिस्टलोग्राफी

संदर्भ

• Bamberg, John; Cairns, Grant; Kilminster, Devin (March 2003), "The crystallographic restriction, permutations, and Goldbach's conjecture" (PDF), American Mathematical Monthly, 110 (3): 202–209, CiteSeerX 10.1.1.124.8582, doi:10.2307/3647934, JSTOR 3647934
• Elliott, Stephen (1998), The Physics and Chemistry of Solids, Wiley, ISBN 978-0-471-98194-7
• Coxeter, H. S. M. (1989), Introduction to Geometry (2nd ed.), Wiley, ISBN 978-0-471-50458-0
• Scherrer, W. (1946), "Die Einlagerung eines regulären Vielecks in ein Gitter", Elemente der Mathematik, 1 (6): 97–98
• Shechtman, D.; Blech, I.; Gratias, D.; Cahn, JW (1984), "Metallic phase with long-range orientational order and no translational symmetry", Physical Review Letters, 53 (20): 1951–1953, Bibcode:1984PhRvL..53.1951S, doi:10.1103/PhysRevLett.53.1951

बाहरी संबंध

• The crystallographic restriction