पी (जटिलता)

कम्प्यूटेशनल जटिलता सिद्धांत में, P, जिसे PTIME या DTIME(n के रूप में भी जाना जाता है^O(1)), एक मौलिक जटिलता वर्ग है। इसमें सभी निर्णय समस्याएं शामिल हैं जिन्हें नियतात्मक ट्यूरिंग मशीन द्वारा गणना समय, या बहुपद समय की बहुपद राशि का उपयोग करके हल किया जा सकता है।

कोभम की थीसिस का मानना है कि पी कम्प्यूटेशनल समस्याओं का वर्ग है जो कुशलता से हल करने योग्य या ट्रैक्टेबल समस्या है। यह अचूक है: व्यवहार में, P में ज्ञात कुछ समस्याओं का व्यावहारिक समाधान नहीं है, और कुछ जो P में नहीं हैं, लेकिन यह अंगूठे का एक उपयोगी नियम है।

परिभाषा

एक औपचारिक भाषा एल पी में है अगर और केवल तभी निर्धारिती ट्यूरिंग मशीन एम मौजूद है, जैसे कि

एम सभी इनपुट पर बहुपद समय के लिए चलता है
एल में सभी एक्स के लिए, एम 1 आउटपुट करता है
एल में नहीं सभी एक्स के लिए, एम 0 आउटपुट करता है

पी को बूलियन सर्किट के एक समान परिवार के रूप में भी देखा जा सकता है। एक भाषा एल पी में है अगर और केवल अगर सर्किट जटिलता मौजूद है $\{C_{n}:n\in \mathbb {N} \}$ , ऐसा है कि

सभी के लिए $n\in \mathbb {N}$ , $C_{n}$ इनपुट के रूप में n बिट्स लेता है और 1 बिट आउटपुट करता है
एल में सभी एक्स के लिए, $C_{|x|}(x)=1$
सभी एक्स के लिए एल में नहीं, $C_{|x|}(x)=0$

जटिलता वर्ग को बदले बिना केवल एक सर्किट जटिलता # लॉगस्पेस वर्दी परिवार का उपयोग करने के लिए सर्किट परिभाषा को कमजोर किया जा सकता है।

== पी == में उल्लेखनीय समस्याएं पी को कई प्राकृतिक समस्याओं के लिए जाना जाता है, जिसमें रैखिक प्रोग्रामिंग के निर्णय संस्करण और अधिकतम मिलान खोजना शामिल है। 2002 में, यह दिखाया गया था कि यह निर्धारित करने की समस्या कि क्या कोई संख्या अभाज्य संख्या है, P में है।^[1] कार्य समस्याओं का संबंधित वर्ग एफपी (जटिलता) है।

पी के लिए कई प्राकृतिक समस्याएं पूर्ण हैं, जिनमें सेंट-कनेक्टिविटी शामिल है। वैकल्पिक ग्राफ पर सेंट-कनेक्टिविटी (या गम्यता)।^[2] पी-पूर्ण | पी-पूर्ण समस्याओं पर आलेख पी में और प्रासंगिक समस्याओं को सूचीबद्ध करता है।

अन्य वर्गों से संबंध

जटिलता वर्गों के बीच संबंध का प्रतिनिधित्व

पी (जटिलता), एनपी (जटिलता), सह-एनपी, बीपीपी (जटिलता), पी/पॉली, पीएच (जटिलता), और पीएसपीएसीई सहित जटिलता वर्गों का समावेश

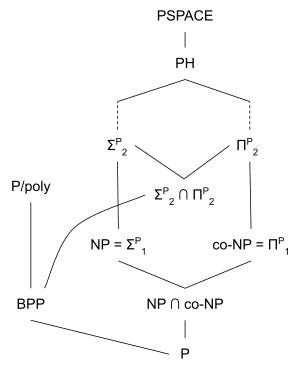
पी का एक सामान्यीकरण एनपी (जटिलता) है, जो बहुपद समय में चलने वाली गैर-नियतात्मक ट्यूरिंग मशीन द्वारा तय की जाने वाली निर्णय समस्याओं का वर्ग है। समतुल्य रूप से, यह निर्णय समस्याओं का वर्ग है जहां प्रत्येक हाँ उदाहरण में बहुपद आकार का प्रमाण पत्र होता है, और बहुपद समय निर्धारक ट्यूरिंग मशीन द्वारा प्रमाणपत्रों की जाँच की जा सकती है। समस्याओं का वर्ग जिसके लिए यह बिना किसी उदाहरण के सत्य है, को-एनपी कहा जाता है। पी तुच्छ रूप से एनपी और सह-एनपी का एक उपसमूह है; अधिकांश विशेषज्ञ मानते हैं कि यह एक उचित उपसमुच्चय है,^[3] हालांकि यह विश्वास ( ${\mathsf {P}}\subsetneq {\mathsf {NP}}$ परिकल्पना) पी बनाम एनपी समस्या। एक और खुली समस्या यह है कि क्या एनपी = सह-एनपी; चूंकि पी = सह-पी,^[4] एक नकारात्मक उत्तर का अर्थ होगा ${\mathsf {P}}\subsetneq {\mathsf {NP}}$ .

पी को कम से कम एल (जटिलता) के रूप में भी जाना जाता है, मेमोरी स्पेस (कम्प्यूटेशनल संसाधन) की लॉगरिदमिक मात्रा में समस्याओं का वर्ग। एक निर्णायक उपयोग कर रहा है $O(\log n)$ अंतरिक्ष से अधिक का उपयोग नहीं कर सकता $2^{O(\log n)}=n^{O(1)}$ समय, क्योंकि यह संभावित विन्यासों की कुल संख्या है; इस प्रकार, L, P का एक उपसमुच्चय है। एक अन्य महत्वपूर्ण समस्या यह है कि क्या L = P. हम जानते हैं कि P = AL, वैकल्पिक ट्यूरिंग मशीनों द्वारा लॉगरिदमिक मेमोरी में हल की जाने वाली समस्याओं का सेट। पी को पीएसपीएसीई से बड़ा नहीं माना जाता है, बहुपद अंतरिक्ष में निर्णय लेने योग्य समस्याओं का वर्ग। फिर, क्या पी = पीएसपीएसीई एक खुली समस्या है। संक्षेप में:

{\mathsf {L}}\subseteq {\mathsf {AL}}={\mathsf {P}}\subseteq {\mathsf {NP}}\subseteq {\mathsf {PSPACE}}\subseteq {\mathsf {EXPTIME}}.

यहाँ, EXPTIME घातीय समय में हल करने योग्य समस्याओं का वर्ग है। ऊपर दिखाए गए सभी वर्गों में से केवल दो सख्त नियंत्रण ज्ञात हैं:

P EXPTIME में सख्ती से निहित है। नतीजतन, सभी EXPTIME- कठिन समस्याएं P के बाहर हैं, और ऊपर P के दाईं ओर कम से कम एक सख्त है (वास्तव में, यह व्यापक रूप से माना जाता है कि तीनों सख्त हैं)।
L सख्ती से PSPACE में निहित है।

P में सबसे कठिन समस्याएँ P-पूर्ण समस्याएँ हैं।

P का एक अन्य सामान्यीकरण P/poly, या Nonuniform Polynomial-Time है। यदि कोई समस्या पी/पॉली में है, तो इसे नियतात्मक बहुपद समय में हल किया जा सकता है, बशर्ते कि एक सलाह (जटिलता) दी जाए जो केवल इनपुट की लंबाई पर निर्भर करती है। एनपी के विपरीत, हालांकि, बहुपद-समय मशीन को धोखाधड़ी सलाह स्ट्रिंग का पता लगाने की आवश्यकता नहीं है; यह एक सत्यापनकर्ता नहीं है। पी/पॉली एक बड़ा वर्ग है जिसमें लगभग सभी व्यावहारिक समस्याएं हैं, जिसमें सभी परिबद्ध-त्रुटि संभाव्य बहुपद शामिल हैं। यदि इसमें एनपी शामिल है, तो बहुपद पदानुक्रम दूसरे स्तर पर गिर जाता है। दूसरी ओर, इसमें कुछ अव्यावहारिक समस्याएँ भी शामिल हैं, जिनमें कुछ अनिर्णीत समस्याएँ भी शामिल हैं, जैसे कि किसी भी अनिर्णीत समस्या का एकात्मक संस्करण।

1999 में, जिन-यी कै और डी. शिवकुमार ने हिकारू ओगिहारा के काम पर निर्माण किया, ने दिखाया कि यदि कोई विरल भाषा मौजूद है जो पी-पूर्ण है, तो एल = पी।^[5]

P संभाव्य जटिलता वर्गों (ZPP (जटिलता), RP (जटिलता), सह-RP, BPP (जटिलता), BQP, PP (जटिलता)) के संबंध में, सभी PSPACE के भीतर। यह ज्ञात नहीं है कि इनमें से कोई भी नियंत्रण सख्त है या नहीं।

P BQP में निहित है, यह अज्ञात है कि क्या रोकथाम सख्त है।

गुण

बहुपद-समय एल्गोरिदम रचना के तहत बंद हैं। सहजता से, यह कहता है कि यदि कोई ऐसा फ़ंक्शन लिखता है जो बहुपद-समय है, यह मानते हुए कि फ़ंक्शन कॉल स्थिर-समय हैं, और यदि उन कार्यों को स्वयं बहुपद समय की आवश्यकता होती है, तो संपूर्ण एल्गोरिथ्म बहुपद समय लेता है। इसका एक परिणाम यह है कि P स्वयं के लिए कम (जटिलता) है। यह भी एक मुख्य कारण है कि P को एक मशीन-स्वतंत्र वर्ग माना जाता है; किसी भी मशीन की सुविधा, जैसे कि रैंडम एक्सेस, जिसे बहुपद समय में सिम्युलेट किया जा सकता है, इसे मुख्य बहुपद-समय एल्गोरिथ्म के साथ एक अधिक बुनियादी मशीन पर बहुपद-समय एल्गोरिथ्म में कम करने के लिए बनाया जा सकता है।

P में भाषाएँ उत्क्रमण, चौराहा (सेट सिद्धांत) , संघ (सेट सिद्धांत) , कॉन्टेनेशन, क्लीन क्लोजर, इनवर्स समरूपता और कॉम्प्लीमेंट (जटिलता) के तहत भी बंद हैं।^[6]

बहुपद-समय एल्गोरिदम के शुद्ध अस्तित्व प्रमाण

कुछ समस्याओं को बहुपद समय में हल करने योग्य माना जाता है, लेकिन उन्हें हल करने के लिए कोई ठोस एल्गोरिथम ज्ञात नहीं है। उदाहरण के लिए, रॉबर्टसन-सीमोर प्रमेय गारंटी देता है कि वर्जित अवयस्कों की एक परिमित सूची है जो एक टोरस पर एम्बेड किए जा सकने वाले ग्राफ़ के सेट की विशेषता (उदाहरण के लिए) है; इसके अलावा, रॉबर्टसन और सीमोर ने दिखाया कि एक O(n³) एल्गोरिथम यह निर्धारित करने के लिए कि क्या किसी ग्राफ़ में माइनर के रूप में दिया गया ग्राफ़ है। यह एक गैर-रचनात्मक प्रमाण उत्पन्न करता है कि यह निर्धारित करने के लिए एक बहुपद-समय एल्गोरिथ्म है कि क्या किसी दिए गए ग्राफ को टोरस पर एम्बेड किया जा सकता है, इस तथ्य के बावजूद कि इस समस्या के लिए कोई ठोस एल्गोरिदम ज्ञात नहीं है।

वैकल्पिक लक्षण वर्णन

[[वर्णनात्मक जटिलता]] में, पी को एफओ (एलएफपी) में अभिव्यक्त होने वाली समस्याओं के रूप में वर्णित किया जा सकता है, आदेशित संरचनाओं पर कम से कम निश्चित बिंदु ऑपरेटर के साथ प्रथम-क्रम तर्क जोड़ा गया है। इमेरमैन की वर्णनात्मक जटिलता में,^[7] इमरमैन इस परिणाम का श्रेय वर्दी को देते हैं^[8] और इमेरमैन को।^[9] यह 2001 में प्रकाशित हुआ था कि PTIME (सकारात्मक) रेंज कॉन्सटेनेशन व्याकरण से मेल खाता है।^[10] पी को उन समस्याओं के लिए एल्गोरिथम जटिलता वर्ग के रूप में भी परिभाषित किया जा सकता है जो निर्णय की समस्या नहीं हैं^[11] (भले ही, उदाहरण के लिए, बहुपद समय में 2-संतोषजनक उदाहरण का समाधान खोजने से संबंधित निर्णय समस्या के लिए स्वचालित रूप से बहुपद एल्गोरिदम मिलता है)। उस मामले में पी एनपी का उप-समूह नहीं है, लेकिन पी∩डीईसी है, जहां डीईसी निर्णय समस्याओं का वर्ग है।

इतिहास

डेक्सटर कोजेन^[12] बताता है कि एलन कोभम (गणितज्ञ) और जैक एडमंड्स को आम तौर पर बहुपद समय की धारणा के आविष्कार का श्रेय दिया जाता है। कोभम ने कुशल एल्गोरिदम को चित्रित करने के एक मजबूत तरीके के रूप में कक्षा का आविष्कार किया, जिससे कोहम की थीसिस की ओर अग्रसर हुआ। हालांकि, हेनरी कैबॉर्न पॉकलिंगटन|एच. सी पॉकलिंगटन, 1910 के पेपर में,^[13]^[14] द्विघात सर्वांगसमताओं को हल करने के लिए दो एल्गोरिदम का विश्लेषण किया, और देखा कि किसी ने मापांक के लघुगणक की शक्ति के समानुपाती समय लिया और इसकी तुलना उस एक के साथ की जो स्वयं मापांक या इसके वर्गमूल के लिए आनुपातिक समय लेता है, इस प्रकार स्पष्ट रूप से एक एल्गोरिथ्म के बीच अंतर करता है जो बहुपद समय में चलता था बनाम जो नहीं चलता था।

↑ Manindra Agrawal, Neeraj Kayal, Nitin Saxena, "PRIMES is in P", Annals of Mathematics 160 (2004), no. 2, pp. 781–793.
↑ Immerman, Neil (1999). वर्णनात्मक जटिलता. New York: Springer-Verlag. ISBN 978-0-387-98600-5.
↑ Johnsonbaugh, Richard; Schaefer, Marcus, Algorithms, 2004 Pearson Education, page 458, ISBN 0-02-360692-4
↑ "complexity theory - Why is co-P = P". Stack Overflow. Archived from the original on 14 October 2020. Retrieved 2020-10-14.
↑ Jin-Yi Cai and D. Sivakumar. Sparse hard sets for P: resolution of a conjecture of Hartmanis. Journal of Computer and System Sciences, volume 58, issue 2, pp.280–296. 1999. ISSN 0022-0000. At Citeseer
↑ Hopcroft, John E.; Rajeev Motwani; Jeffrey D. Ullman (2001). ऑटोमेटा सिद्धांत, भाषाओं और संगणना का परिचय (2. ed.). Boston: Addison-Wesley. pp. 425–426. ISBN 978-0201441246.
↑ Immerman, Neil (1999). वर्णनात्मक जटिलता. New York: Springer-Verlag. p. 66. ISBN 978-0-387-98600-5.
↑ Vardi, Moshe Y. (1982). "संबंधपरक क्वेरी भाषाओं की जटिलता". STOC '82: Proceedings of the fourteenth annual ACM symposium on Theory of computing. pp. 137–146. doi:10.1145/800070.802186.
↑ Immerman, Neil (1982). "बहुपद समय में संगणनीय संबंधपरक प्रश्न". STOC '82: Proceedings of the fourteenth annual ACM symposium on Theory of computing. pp. 147–152. doi:10.1145/800070.802187. Revised version in Information and Control, 68 (1986), 86–104.
↑ Laura Kallmeyer (2010). प्रसंग-मुक्त व्याकरण से परे पार्सिंग. Springer Science & Business Media. pp. 5 and 37. ISBN 978-3-642-14846-0. citing http://mjn.host.cs.st-andrews.ac.uk/publications/2001d.pdf for the proof
↑ Wegener, Ingo (2005). जटिलता सिद्धांत. Springer-Verlag. p. 35. doi:10.1007/3-540-27477-4. ISBN 978-3-540-21045-0.
↑ Kozen, Dexter C. (2006). संगणना का सिद्धांत. Springer. p. 4. ISBN 978-1-84628-297-3.
↑ Pocklington, H. C. (1910–1912). "उस घातांक का निर्धारण जिससे कोई संख्या संबंधित है, कुछ सर्वांगसमताओं का व्यावहारिक समाधान, और द्विघात पारस्परिकता का नियम". Proc. Camb. Phil. Soc. 16: 1–5.
↑ Gautschi, Walter (1994). Mathematics of computation, 1943–1993: a half-century of computational mathematics: Mathematics of Computation 50th Anniversary Symposium, August 9–13, 1993, Vancouver, British Columbia. Providence, RI: American Mathematical Society. pp. 503–504. ISBN 978-0-8218-0291-5.

संदर्भ

Cobham, Alan (1965). "The intrinsic computational difficulty of functions". Proc. Logic, Methodology, and Philosophy of Science II. North Holland.
Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw–Hill, 2001. ISBN 0-262-03293-7. Section 34.1: Polynomial time, pp. 971–979.
Papadimitriou, Christos H. (1994). Computational complexity. Reading, Mass.: Addison–Wesley. ISBN 978-0-201-53082-7.
Sipser, Michael (2006). Introduction to the Theory of Computation, 2nd Edition. Course Technology Inc. ISBN 978-0-534-95097-2. Section 7.2: The Class P, pp. 256–263;.

बाहरी संबंध

Complexity Zoo: Class P
Complexity Zoo: Class P/poly

[1] Manindra Agrawal, Neeraj Kayal, Nitin Saxena, "PRIMES is in P", Annals of Mathematics 160 (2004), no. 2, pp. 781–793.

[Immerman_Reachability-2] Immerman, Neil (1999). वर्णनात्मक जटिलता. New York: Springer-Verlag. ISBN 978-0-387-98600-5.

[3] Johnsonbaugh, Richard; Schaefer, Marcus, Algorithms, 2004 Pearson Education, page 458, ISBN 0-02-360692-4

[4] "complexity theory - Why is co-P = P". Stack Overflow. Archived from the original on 14 October 2020. Retrieved 2020-10-14.

[5] Jin-Yi Cai and D. Sivakumar. Sparse hard sets for P: resolution of a conjecture of Hartmanis. Journal of Computer and System Sciences, volume 58, issue 2, pp.280–296. 1999. ISSN 0022-0000. At Citeseer

[6] Hopcroft, John E.; Rajeev Motwani; Jeffrey D. Ullman (2001). ऑटोमेटा सिद्धांत, भाषाओं और संगणना का परिचय (2. ed.). Boston: Addison-Wesley. pp. 425–426. ISBN 978-0201441246.

[7] Immerman, Neil (1999). वर्णनात्मक जटिलता. New York: Springer-Verlag. p. 66. ISBN 978-0-387-98600-5.

[8] Vardi, Moshe Y. (1982). "संबंधपरक क्वेरी भाषाओं की जटिलता". STOC '82: Proceedings of the fourteenth annual ACM symposium on Theory of computing. pp. 137–146. doi:10.1145/800070.802186.

[9] Immerman, Neil (1982). "बहुपद समय में संगणनीय संबंधपरक प्रश्न". STOC '82: Proceedings of the fourteenth annual ACM symposium on Theory of computing. pp. 147–152. doi:10.1145/800070.802187. Revised version in Information and Control, 68 (1986), 86–104.

[Kallmeyer2010-10] Laura Kallmeyer (2010). प्रसंग-मुक्त व्याकरण से परे पार्सिंग. Springer Science & Business Media. pp. 5 and 37. ISBN 978-3-642-14846-0. citing http://mjn.host.cs.st-andrews.ac.uk/publications/2001d.pdf for the proof

[Wegener2005-11] Wegener, Ingo (2005). जटिलता सिद्धांत. Springer-Verlag. p. 35. doi:10.1007/3-540-27477-4. ISBN 978-3-540-21045-0.

[12] Kozen, Dexter C. (2006). संगणना का सिद्धांत. Springer. p. 4. ISBN 978-1-84628-297-3.

[13] Pocklington, H. C. (1910–1912). "उस घातांक का निर्धारण जिससे कोई संख्या संबंधित है, कुछ सर्वांगसमताओं का व्यावहारिक समाधान, और द्विघात पारस्परिकता का नियम". Proc. Camb. Phil. Soc. 16: 1–5.

[14] Gautschi, Walter (1994). Mathematics of computation, 1943–1993: a half-century of computational mathematics: Mathematics of Computation 50th Anniversary Symposium, August 9–13, 1993, Vancouver, British Columbia. Providence, RI: American Mathematical Society. pp. 503–504. ISBN 978-0-8218-0291-5.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

v t e Important complexity classes (more)
Considered feasible	DLOGTIME AC⁰ ACC⁰ TC⁰ L SL RL NL NC SC CC P P-complete ZPP RP BPP BQP APX FP
Suspected infeasible	UP NP NP-complete NP-hard co-NP co-NP-complete AM QMA PH ⊕P PP #P #P-complete IP PSPACE PSPACE-complete
Considered infeasible	EXPTIME NEXPTIME EXPSPACE 2-EXPTIME ELEMENTARY PR R RE ALL
Class hierarchies	Polynomial hierarchy Exponential hierarchy Grzegorczyk hierarchy Arithmetical hierarchy Boolean hierarchy
Families of classes	DTIME NTIME DSPACE NSPACE Probabilistically checkable proof Interactive proof system

पी (जटिलता)

Contents