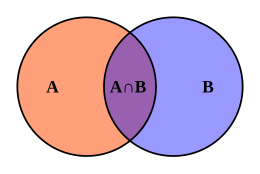
आवश्यकता एवं पर्याप्तता

तर्क और गणित में, आवश्यकता और पर्याप्तता दो कथनों (तर्क) के बीच एक भौतिक सशर्त या निहितार्थ संबंध का वर्णन करने के लिए उपयोग किए जाने वाले शब्द हैं। उदाहरण के लिए, सशर्त वाक्य में: यदि $P$ तब $Q$ , $Q$ के लिए आवश्यक है $P$ , क्योंकि सत्य का मूल्य $Q$ की सत्यता की गारंटी है $P$ . (समान रूप से, यह होना असंभव है $P$ बिना $Q$ , या का मिथ्यात्व $Q$ की मिथ्याता सुनिश्चित करता है $P$ .)^[1] इसी प्रकार, $P$ के लिए पर्याप्त है $Q$ , क्योंकि $P$ सत्य होने का तात्पर्य हमेशा यही होता है $Q$ सच है, लेकिन $P$ सच नहीं होने का मतलब हमेशा यह नहीं होता है $Q$ यह सच नहीं है।^[2] सामान्य तौर पर, एक आवश्यक शर्त वह होती है (संभवतः कई स्थितियों में से एक) जो किसी अन्य स्थिति के उत्पन्न होने के लिए मौजूद होनी चाहिए, जबकि पर्याप्त स्थिति वह होती है जो उक्त स्थिति उत्पन्न करती है।^[3] यह दावा कि एक कथन दूसरे के लिए एक आवश्यक और पर्याप्त शर्त है, का अर्थ है कि पहला कथन सत्य है यदि और केवल यदि बाद वाला सत्य है। अर्थात्, दोनों कथन या तो एक साथ सत्य होने चाहिए, या एक साथ गलत होने चाहिए।^[4]^[5]^[6] सामान्य अंग्रेजी (प्राकृतिक भाषा में भी) में स्थितियों या मामलों की स्थिति के बीच संबंधों को आवश्यक और पर्याप्त रूप से इंगित किया जाता है, बयानों को नहीं। उदाहरण के लिए, पुरुष होना भाई होने के लिए एक आवश्यक शर्त है, लेकिन यह पर्याप्त नहीं है - जबकि भाई होने के लिए पुरुष सहोदर होना एक आवश्यक और पर्याप्त शर्त है। किसी भी सशर्त कथन में कम से कम एक पर्याप्त शर्त और कम से कम एक आवश्यक शर्त शामिल होती है।

एनालिटिक्स में, आवश्यकता और पर्याप्तता अलग-अलग कारण तर्कों को संदर्भित कर सकती है,^[7] जहां आवश्यक स्थिति विश्लेषण और गुणात्मक तुलनात्मक विश्लेषण का उपयोग रुचि के किसी विशेष परिणाम के लिए शर्तों की आवश्यकता और पर्याप्तता की जांच के लिए विश्लेषणात्मक तकनीकों के रूप में किया जा सकता है।

परिभाषाएँ

सशर्त कथन में, यदि S, तो N, S द्वारा निरूपित अभिव्यक्ति को पूर्ववर्ती (तर्क) कहा जाता है, और N द्वारा निरूपित अभिव्यक्ति को परिणामी कहा जाता है। यह सशर्त कथन कई समतुल्य तरीकों से लिखा जा सकता है, जैसे N यदि S, S केवल यदि N, S का तात्पर्य N से है, N का तात्पर्य S से है, $S \to N$ , $S \Rightarrow N$ और एन जब भी एस .^[8] N की उपरोक्त स्थिति में जब भी S, N को S के लिए एक 'आवश्यक' शर्त कहा जाता है। सामान्य भाषा में, यह कहने के बराबर है कि यदि सशर्त कथन एक सच्चा कथन है, तो परिणामी N सत्य होना चाहिए - यदि S का सत्य होना है (तत्काल नीचे सत्य तालिका का तीसरा स्तंभ देखें)। दूसरे शब्दों में, N के सत्य हुए बिना पूर्ववर्ती S सत्य नहीं हो सकता। यदि एन की विपरीत स्थिति में, तो एस, उदाहरण के लिए, किसी को 'सोक्रेट्स' कहलाने के लिए, किसी को 'नेम्ड' होना आवश्यक है। उसी प्रकार मनुष्य को जीवित रहने के लिए वायु का होना आवश्यक है।^[9] कोई यह भी कह सकता है कि S, N के लिए एक 'पर्याप्त' शर्त है (तुरंत नीचे सत्य तालिका के तीसरे कॉलम को फिर से देखें)। यदि सशर्त कथन सत्य है, तो यदि S सत्य है, तो N भी सत्य होना चाहिए; जबकि यदि सशर्त कथन सत्य है और N सत्य है, तो S सत्य या गलत हो सकता है। सामान्य शब्दों में, S की सच्चाई N की सच्चाई की गारंटी देती है।^[9]उदाहरण के लिए, पिछले उदाहरण से आगे बढ़ते हुए, कोई कह सकता है कि यह जानना कि किसी को एसओक्रेटिस कहा जाता है, यह जानने के लिए पर्याप्त है कि किसी के पास एनएम है।

एक आवश्यक और पर्याप्त शर्त के लिए दोनों निहितार्थों की आवश्यकता होती है $S\Rightarrow N$ और $N\Rightarrow S$ (जिसका उत्तरार्द्ध इस प्रकार भी लिखा जा सकता है $S\Leftarrow N$ ) पकड़ना। पहला निहितार्थ बताता है कि S, N के लिए एक पर्याप्त शर्त है, जबकि दूसरा निहितार्थ बताता है कि S, N के लिए एक आवश्यक शर्त है। इसे इस रूप में व्यक्त किया जाता है कि S, N, S के लिए आवश्यक और पर्याप्त है यदि और केवल यदि N, या $S\Leftrightarrow N$ .

Truth table
$S$	$N$	$S\Rightarrow N$	$S\Leftarrow N$	$S\Leftrightarrow N$
T	T	T	T	T
T	F	F	T	F
F	T	T	F	F
F	F	T	T	T

आवश्यकता

सीधी धूप के लिए सूर्य का क्षितिज से ऊपर होना एक आवश्यक शर्त है; लेकिन यह पर्याप्त स्थिति नहीं है, क्योंकि किसी और चीज़ की छाया पड़ सकती है, उदाहरण के लिए, सूर्य ग्रहण के मामले में चंद्रमा।

यह दावा कि Q, P के लिए आवश्यक है, बोलचाल की भाषा में P के समतुल्य है, तब तक सत्य नहीं हो सकता जब तक कि Q सत्य न हो या यदि Q गलत है, तो P गलत है।^[9]^[1]अंतर्विरोध द्वारा, यह वही बात है जैसे जब भी P सत्य होता है, तो Q भी सत्य होता है।

पी और क्यू के बीच तार्किक संबंध को इस प्रकार व्यक्त किया जाता है यदि पी, फिर क्यू और निरूपित पी ⇒ क्यू (पी तार्किक परिणाम क्यू)। इसे P में से किसी एक के रूप में भी व्यक्त किया जा सकता है यदि Q , Q , यदि P , Q जब भी P , और Q जब P . उदाहरण के लिए, गणितीय गद्य में अक्सर कई आवश्यक शर्तें पाई जाती हैं, जो एक साथ मिलकर एक पर्याप्त स्थिति का निर्माण करती हैं (अर्थात, व्यक्तिगत रूप से आवश्यक और संयुक्त रूप से पर्याप्त)^[9]), जैसा कि उदाहरण 5 में दिखाया गया है।

उदाहरण 1

यह सत्य होने के लिए कि जॉन कुंवारा है, यह आवश्यक है कि यह भी सत्य हो कि वह कुंवारा है

अविवाहित,
नर,
वयस्क,

चूंकि यह बताने के लिए कि जॉन कुंवारा है, इसका मतलब है कि जॉन के पास उन तीन अतिरिक्त विधेय (गणितीय तर्क) में से प्रत्येक है।

उदाहरण 2: दो से बड़ी पूर्ण संख्याओं के लिए, अभाज्य होने के लिए विषम होना आवश्यक है, क्योंकि दो ही एकमात्र पूर्ण संख्या है जो सम और अभाज्य दोनों है।

उदाहरण 3: गड़गड़ाहट पर विचार करें, जो बिजली के कारण होने वाली ध्वनि है। एक का कहना है कि बिजली के लिए गड़गड़ाहट आवश्यक है, क्योंकि बिजली कभी भी बिना गड़गड़ाहट के नहीं बनती। जब भी बिजली चमकती है, गड़गड़ाहट होती है। गड़गड़ाहट के कारण बिजली नहीं चमकती (क्योंकि बिजली के कारण गड़गड़ाहट होती है), लेकिन क्योंकि बिजली हमेशा गड़गड़ाहट के साथ आती है, हम कहते हैं कि बिजली के लिए गड़गड़ाहट आवश्यक है। (अर्थात्, औपचारिक अर्थ में, आवश्यकता का अर्थ कार्य-कारण नहीं है।)

उदाहरण 4: अमेरिकी सीनेट में सेवा देने के लिए कम से कम 30 वर्ष की आयु होना आवश्यक है। अगर आपकी उम्र 30 साल से कम है तो आपके लिए सीनेटर बनना असंभव है। यानी अगर आप सीनेटर हैं तो इसका मतलब यह है कि आपकी उम्र कम से कम 30 साल होनी चाहिए।

उदाहरण 5: बीजगणित में, कुछ सेट (गणित) एस के लिए एक बाइनरी ऑपरेशन के साथ $\star$ एक समूह (गणित) बनाने के लिए यह आवश्यक है $\star$ सहयोगी बनें. यह भी आवश्यक है कि S में एक विशेष तत्व e शामिल हो ताकि S में प्रत्येक x के लिए, यह मामला हो कि e $\star$ एक्स और एक्स $\star$ ई दोनों बराबर एक्स. यह भी आवश्यक है कि S में प्रत्येक x के लिए एक संगत तत्व x″ मौजूद हो, जैसे कि दोनों x $\star$ x″ और x″ $\star$ x विशेष तत्व e के बराबर है। इन तीन आवश्यक शर्तों में से कोई भी अपने आप में पर्याप्त नहीं है, लेकिन तीनों का संयोजन (तर्क) है।

पर्याप्तता

किसी ट्रेन का निर्धारित समय पर चलना समय पर पहुंचने के लिए पर्याप्त शर्त हो सकती है (यदि कोई ट्रेन में चढ़ता है और वह समय पर रवाना होती है, तो वह समय पर पहुंचेगा); लेकिन यह हमेशा एक आवश्यक शर्त नहीं है, क्योंकि यात्रा करने के अन्य तरीके भी हैं (यदि ट्रेन समय पर नहीं चलती है, तो भी कोई परिवहन के अन्य साधनों के माध्यम से समय पर पहुंच सकता है)।

यदि P, Q के लिए पर्याप्त है, तो P को सत्य जानना यह निष्कर्ष निकालने के लिए पर्याप्त आधार है कि Q सत्य है; हालाँकि, P को झूठा जानने से यह निष्कर्ष निकालने की न्यूनतम आवश्यकता पूरी नहीं होती है कि Q गलत है।

तार्किक संबंध, पहले की तरह, P, फिर Q या P ⇒ Q के रूप में व्यक्त किया गया है। इसे केवल P के रूप में भी व्यक्त किया जा सकता है यदि Q, P का तात्पर्य Q या कई अन्य वेरिएंट से है। ऐसा हो सकता है कि कई पर्याप्त शर्तें, जब एक साथ ली जाती हैं, तो एक ही आवश्यक शर्त बन जाती है (यानी, व्यक्तिगत रूप से पर्याप्त और संयुक्त रूप से आवश्यक), जैसा कि उदाहरण 5 में दिखाया गया है।

उदाहरण 1: जॉन एक राजा है इसका तात्पर्य यह है कि जॉन पुरुष है। इसलिए यह जानना कि जॉन एक राजा है, यह जानने के लिए पर्याप्त है कि वह एक पुरुष है।

उदाहरण 2: किसी संख्या का 4 से विभाज्य होना उसके सम होने के लिए पर्याप्त (लेकिन आवश्यक नहीं) है, लेकिन 2 से विभाज्य होना उसके सम होने के लिए पर्याप्त और आवश्यक दोनों है।

उदाहरण 3: गड़गड़ाहट की घटना बिजली की घटना के लिए इस अर्थ में पर्याप्त स्थिति है कि गड़गड़ाहट सुनना, और स्पष्ट रूप से इसे इस तरह पहचानना, यह निष्कर्ष निकालना उचित है कि बिजली गिरी है।

उदाहरण 4: यदि अमेरिकी कांग्रेस कोई विधेयक पारित करती है, तो विधेयक पर राष्ट्रपति का हस्ताक्षर इसे कानून बनाने के लिए पर्याप्त है। ध्यान दें कि जिस मामले में राष्ट्रपति ने विधेयक पर हस्ताक्षर नहीं किए, उदाहरण के लिए राष्ट्रपति के वीटो के प्रयोग के माध्यम से#संयुक्त राज्य अमेरिका का मतलब यह नहीं है कि बिल कानून नहीं बन गया है (उदाहरण के लिए, यह अभी भी कांग्रेस के वीटो ओवरराइड के माध्यम से कानून बन सकता है)।

उदाहरण 5: ताश के केंद्र को एक बड़े कुदाल (♠) से चिह्नित किया जाना चाहिए, यह ताश का इक्का बनने के लिए पर्याप्त है। तीन अन्य पर्याप्त शर्तें यह हैं कि कार्ड के केंद्र को एक ही हीरे (♦), दिल (♥), या क्लब (♣) से चिह्नित किया जाना चाहिए। कार्ड के इक्का होने के लिए इनमें से कोई भी शर्त आवश्यक नहीं है, लेकिन उनका विच्छेदन है, क्योंकि इनमें से कम से कम (वास्तव में, बिल्कुल) शर्तों को पूरा किए बिना कोई भी कार्ड इक्का नहीं हो सकता है।

आवश्यकता और पर्याप्तता के बीच संबंध

बैंगनी क्षेत्र में होना A में होने के लिए पर्याप्त है, लेकिन आवश्यक नहीं है। बैंगनी क्षेत्र में रहने के लिए A में होना आवश्यक है, लेकिन पर्याप्त नहीं है। ए में होना और बी में होना बैंगनी क्षेत्र में होने के लिए आवश्यक और पर्याप्त है।

एक शर्त दूसरी न होते हुए भी आवश्यक या पर्याप्त हो सकती है। उदाहरण के लिए, एक स्तनपायी (एन) होना आवश्यक है लेकिन मानव (एस) होने के लिए पर्याप्त नहीं है, और यह एक संख्या है $x$ तर्कसंगत है (एस) पर्याप्त है लेकिन आवश्यक नहीं है $x$ एक वास्तविक संख्या (एन) होना (चूँकि ऐसी वास्तविक संख्याएँ हैं जो तर्कसंगत नहीं हैं)।

एक शर्त आवश्यक और पर्याप्त दोनों हो सकती है। उदाहरण के लिए, वर्तमान में, आज चार जुलाई को संयुक्त राज्य अमेरिका में स्वतंत्रता दिवस (संयुक्त राज्य अमेरिका) के लिए एक आवश्यक और पर्याप्त शर्त है। इसी प्रकारउलटा मैट्रिक्स (गणित) एम के व्युत्क्रम मैट्रिक्स के लिए एक आवश्यक और पर्याप्त शर्त यह है कि एम में एक गैर-शून्य निर्धारक है।

गणितीय रूप से कहें तो, आवश्यकता और पर्याप्तता एक दूसरे के लिए द्वैत (गणित) हैं। किसी भी कथन S और N के लिए, यह दावा कि N, S के लिए आवश्यक है, इस दावे के बराबर है कि S, N के लिए पर्याप्त है। इस द्वंद्व का एक और पहलू यह है कि, जैसा कि ऊपर दिखाया गया है, आवश्यक शर्तों के संयोजन (और का उपयोग करके) पर्याप्तता प्राप्त कर सकते हैं, जबकि पर्याप्त शर्तों के विच्छेदन (या का उपयोग करके) आवश्यकता प्राप्त कर सकते हैं। तीसरे पहलू के लिए, प्रत्येक गणितीय विधेय (गणित) एन को वस्तुओं, घटनाओं या बयानों के सेट टी (एन) के साथ पहचानें जिसके लिए एन सत्य है; फिर S के लिए N की आवश्यकता पर जोर देना यह दावा करने के बराबर है कि T(N) T(S) का एक सुपरसेट है, जबकि N के लिए S की पर्याप्तता पर जोर देना यह दावा करने के बराबर है कि T(S) T(N) का एक सबसेट है ).

मनोवैज्ञानिक रूप से कहें तो, आवश्यकता और पर्याप्तता दोनों अवधारणाओं के शास्त्रीय दृष्टिकोण के प्रमुख पहलू हैं। अवधारणाओं के शास्त्रीय सिद्धांत के तहत, मानव मस्तिष्क किस प्रकार एक श्रेणी ^[10]यह अवधारणाओं के संभाव्य सिद्धांत के विपरीत है जो बताता है कि कोई भी परिभाषित विशेषता आवश्यक या पर्याप्त नहीं है, बल्कि श्रेणियां एक परिवार वृक्ष संरचना से मिलती जुलती हैं।

एक साथ आवश्यकता और पर्याप्तता

यह कहना कि P, Q के लिए आवश्यक और पर्याप्त है, दो बातें कहने जैसा है:

कि P, Q के लिए आवश्यक है, $P\Leftarrow Q$ , और वह P, Q के लिए पर्याप्त है, $P\Rightarrow Q$ .
समान रूप से, यह कहना समझा जा सकता है कि P और Q दूसरे के लिए आवश्यक हैं, $P\Rightarrow Q\land Q\Rightarrow P$ , जिसे यह भी कहा जा सकता है कि प्रत्येक एक दूसरे के लिए पर्याप्त है या उसका तात्पर्य है।

कोई इनमें से किसी भी, और इस प्रकार सभी मामलों को कथन P द्वारा संक्षेपित कर सकता है यदि और केवल यदि Q, जिसे द्वारा दर्शाया गया है $P\Leftrightarrow Q$ , जबकि मामले हमें यही बताते हैं $P\Leftrightarrow Q$ के समान है $P\Rightarrow Q\land Q\Rightarrow P$ .

उदाहरण के लिए, ग्राफ़ सिद्धांत में एक ग्राफ़ G को द्विदलीय ग्राफ़ कहा जाता है यदि इसके प्रत्येक शीर्ष को काला या सफ़ेद रंग इस प्रकार निर्दिष्ट करना संभव हो कि G के प्रत्येक किनारे पर प्रत्येक रंग का एक समापन बिंदु हो। और किसी भी ग्राफ़ के द्विदलीय होने के लिए, यह एक आवश्यक और पर्याप्त शर्त है कि इसमें कोई विषम-लंबाई [[चक्र (ग्राफ सिद्धांत)]] नहीं है। इस प्रकार, यह पता लगाना कि क्या ग्राफ़ में कोई विषम चक्र है, यह बताता है कि क्या यह द्विदलीय है और इसके विपरीत भी। एक दार्शनिक^[11] इस स्थिति को इस प्रकार चित्रित किया जा सकता है: यद्यपि द्विदलीयता और विषम चक्रों की अनुपस्थिति की अवधारणाएं इरादे में भिन्न हैं, उनका विस्तार (शब्दार्थ) समान है।^[12] गणित में, प्रमेयों को अक्सर इस रूप में कहा जाता है कि P सत्य है यदि और केवल यदि Q सत्य है। क्योंकि, जैसा कि पिछले भाग में बताया गया है, एक की दूसरे के लिए आवश्यकता पहले वाले के लिए दूसरे की पर्याप्तता के बराबर है, उदाहरण के लिए $P\Leftarrow Q$ तार्किक तुल्यता है $Q\Rightarrow P$ , यदि P, Q के लिए आवश्यक और पर्याप्त है, तो Q, P के लिए आवश्यक और पर्याप्त है। हम लिख सकते हैं $P\Leftrightarrow Q\equiv Q\Leftrightarrow P$ और कहें कि कथन P सत्य है यदि और केवल यदि Q सत्य है और Q सत्य है यदि और केवल यदि P सत्य है तो समतुल्य हैं।

यह भी देखें

संदर्भ

↑ ^1.0 ^1.1 "[M06] Necessity and sufficiency". philosophy.hku.hk. Retrieved 2019-12-02.
↑ Bloch, Ethan D. (2011). Proofs and Fundamentals: A First Course in Abstract Mathematics. Springer. pp. 8–9. ISBN 978-1-4419-7126-5.
↑ Confusion-of-Necessary (2019-05-15). "पर्याप्त स्थिति के साथ आवश्यक का भ्रम". www.txstate.edu. Retrieved 2019-12-02.
↑ Betz, Frederick (2011). Managing Science: Methodology and Organization of Research. New York: Springer. p. 247. ISBN 978-1-4419-7487-7.
↑ Manktelow, K. I. (1999). तर्क और विचार. East Sussex, UK: Psychology Press. ISBN 0-86377-708-2.
↑ Asnina, Erika; Osis, Janis & Jansone, Asnate (2013). "टोपोलॉजिकल संबंधों की औपचारिक विशिष्टता". Databases and Information Systems VII. 249 (Databases and Information Systems VII): 175. doi:10.3233/978-1-61499-161-8-175.
↑ Richter, Nicole Franziska; Hauff, Sven (2022-08-01). "Necessary conditions in international business research–Advancing the field with a new perspective on causality and data analysis". Journal of World Business. 57 (5): 101310. doi:10.1016/j.jwb.2022.101310. ISSN 1090-9516.
↑ Devlin, Keith (2004), Sets, Functions and Logic / An Introduction to Abstract Mathematics (3rd ed.), Chapman & Hall, pp. 22–23, ISBN 978-1-58488-449-1
↑ ^9.0 ^9.1 ^9.2 ^9.3 "आवश्यक शर्तों और पर्याप्त शर्तों की अवधारणा". www.sfu.ca. Retrieved 2019-12-02.
↑ "Classical Theory of Concepts, the | Internet Encyclopedia of Philosophy".
↑ Stanford University primer, 2006.
↑ "Meanings, in this sense, are often called intensions, and things designated, extensions. Contexts in which extension is all that matters are, naturally, called extensional, while contexts in which extension is not enough are intensional. Mathematics is typically extensional throughout." Stanford University primer, 2006.

बाहरी संबंध

Critical thinking web tutorial: Necessary and Sufficient Conditions
Simon Fraser University: Concepts with examples

[:0-1] 1.0 ^1.1 "[M06] Necessity and sufficiency". philosophy.hku.hk. Retrieved 2019-12-02.

[2] Bloch, Ethan D. (2011). Proofs and Fundamentals: A First Course in Abstract Mathematics. Springer. pp. 8–9. ISBN 978-1-4419-7126-5.

[3] Confusion-of-Necessary (2019-05-15). "पर्याप्त स्थिति के साथ आवश्यक का भ्रम". www.txstate.edu. Retrieved 2019-12-02.

[betz-4] Betz, Frederick (2011). Managing Science: Methodology and Organization of Research. New York: Springer. p. 247. ISBN 978-1-4419-7487-7.

[Manktelow-5] Manktelow, K. I. (1999). तर्क और विचार. East Sussex, UK: Psychology Press. ISBN 0-86377-708-2.

[asnina-6] Asnina, Erika; Osis, Janis & Jansone, Asnate (2013). "टोपोलॉजिकल संबंधों की औपचारिक विशिष्टता". Databases and Information Systems VII. 249 (Databases and Information Systems VII): 175. doi:10.3233/978-1-61499-161-8-175.

[7] Richter, Nicole Franziska; Hauff, Sven (2022-08-01). "Necessary conditions in international business research–Advancing the field with a new perspective on causality and data analysis". Journal of World Business. 57 (5): 101310. doi:10.1016/j.jwb.2022.101310. ISSN 1090-9516.

[8] Devlin, Keith (2004), Sets, Functions and Logic / An Introduction to Abstract Mathematics (3rd ed.), Chapman & Hall, pp. 22–23, ISBN 978-1-58488-449-1

[:2-9] 9.0 ^9.1 ^9.2 ^9.3 "आवश्यक शर्तों और पर्याप्त शर्तों की अवधारणा". www.sfu.ca. Retrieved 2019-12-02.

[10] "Classical Theory of Concepts, the | Internet Encyclopedia of Philosophy".

[stan-11] Stanford University primer, 2006.

[12] "Meanings, in this sense, are often called intensions, and things designated, extensions. Contexts in which extension is all that matters are, naturally, called extensional, while contexts in which extension is not enough are intensional. Mathematics is typically extensional throughout." Stanford University primer, 2006.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]