प्रक्षेपी हार्मोनिक संयुग्म

D का हार्मोनिक संयुग्म है C इसके संबंध में A और B.
A, D, B, C एक हार्मोनिक रेंज बनाते हैं।
KLMN इसे उत्पन्न करने वाला एक पूर्ण चतुर्भुज है।

प्रक्षेपी ज्यामिति में, वास्तविक प्रक्षेपी रेखा पर बिंदुओं के क्रमित ट्रिपल के हार्मोनिक संयुग्म बिंदु को निम्नलिखित निर्माण द्वारा परिभाषित किया गया है:

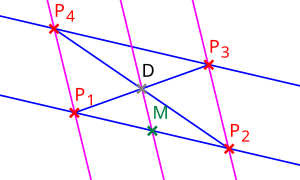
तीन संरेख बिंदु दिए गए हैं A, B, C, होने देना L उनके शामिल होने पर कोई बिंदु नहीं होना चाहिए और किसी भी रेखा को जाने देना चाहिए C मिलना LA, LB पर M, N क्रमश। अगर AN और BM यहां मिलना K, और LK मिलते हैं AB पर D, तब D का हार्मोनिक संयुग्मी कहा जाता है C इसके संबंध में A, B.

बिंदु D किस बिंदु पर निर्भर नहीं करता है L प्रारंभ में लिया जाता है, किस लाइन पर नहीं C खोजने के लिए प्रयोग किया जाता है M और N. यह तथ्य Desargues प्रमेय से आता है।

वास्तविक प्रक्षेपी ज्यामिति में, हार्मोनिक संयुग्मन को क्रॉस-अनुपात के रूप में भी परिभाषित किया जा सकता है(A, B; C, D) = −1.

क्रॉस-अनुपात मानदंड

चार बिंदुओं को कभी-कभी प्रक्षेप्य सीमा (वास्तविक प्रोजेक्टिव लाइन पर) कहा जाता है क्योंकि यह पाया जाता है D हमेशा खंड को विभाजित करता है AB आंतरिक रूप से उसी अनुपात में C विभाजित करता है AB बाह्य रूप से। वह है:

$|AC|:|BC|=|AD|:|DB|\,.$

यदि ये खंड अब वास्तविक संख्याओं की सामान्य मीट्रिक व्याख्या के साथ संपन्न हैं, तो वे हस्ताक्षरित होंगे और क्रॉस अनुपात (कभी-कभी दोहरा अनुपात) के रूप में जाना जाने वाला एक दोहरा अनुपात बनाते हैं।

$(A,B;C,D)={\frac {|AC|}{|AD|}}\left/{\frac {|BC|}{-|DB|}}\right.,$

जिसके लिए एक हार्मोनिक श्रेणी को -1 के मान से अभिलक्षित किया जाता है। इसलिए हम लिखते हैं:

$(A,B;C,D)={\frac {|AC|}{|AD|}}\cdot {\frac {|BD|}{|BC|}}=-1.$

सामान्य क्रॉस-अनुपात#छह_क्रॉस-अनुपात में एक क्रॉस अनुपात का मान, क्योंकि यह सेगमेंट के चयन के क्रम पर निर्भर करता है (और ऐसे छह चयन संभव हैं)। लेकिन विशेष रूप से हार्मोनिक श्रेणी के लिए क्रॉस अनुपात के केवल तीन मान हैं: {−1, 1/2, 2}, चूंकि -1 स्व-प्रतिलोम है - इसलिए अंतिम दो बिंदुओं का आदान-प्रदान केवल इन मूल्यों में से प्रत्येक का आदान-प्रदान करता है, लेकिन कोई नया मूल्य नहीं पैदा करता है, और इसे शास्त्रीय रूप से हार्मोनिक क्रॉस-अनुपात के रूप में जाना जाता है।

दोहरे अनुपात के संदर्भ में, दिए गए अंक a और b affine रेखा पर, विभाजन अनुपात एक बिंदु का x है

$t(x)={\frac {x-a}{x-b}}.$

ध्यान दें कि कब a < x < b, तब t(x) ऋणात्मक है, और यह अंतराल के बाहर धनात्मक है। पार अनुपात $(c,d;a,b)={\tfrac {t(c)}{t(d)}}$ विभाजन अनुपात का अनुपात है, या दोहरा अनुपात है। दोहरे अनुपात को ऋणात्मक एक पर सेट करने का अर्थ है कि कब t(c) + t(d) = 0, तब c और d के संबंध में हार्मोनिक संयुग्म हैं a और b. तो विभाजन अनुपात मानदंड यह है कि वे योगात्मक व्युत्क्रम हैं।

एक रेखा खंड का हार्मोनिक विभाजन अपोलोनियन हलकों का एक विशेष मामला है। सर्कल की अपोलोनियस की परिभाषा।

कुछ स्कूल अध्ययनों में हार्मोनिक श्रेणी के विन्यास को हार्मोनिक डिवीजन कहा जाता है।

मध्यबिंदु का

मध्यबिंदु और अनंत हार्मोनिक संयुग्म हैं।

कब x से खंड का मध्यबिंदु है a को b, तब

$t(x)={\frac {x-a}{x-b}}=-1.$

क्रॉस-अनुपात मानदंड से, के हार्मोनिक संयुग्म x होगा y कब t(y) = 1. लेकिन इसका कोई निश्चित समाधान नहीं है y के माध्यम से लाइन पर a और b. फिर भी,

$\lim _{y\to \infty }t(y)=1,$

इस प्रकार प्रोजेक्टिव लाइन में अनंत पर एक बिंदु को शामिल करने के लिए प्रेरित करना। अनंत पर यह बिंदु मध्यबिंदु के हार्मोनिक संयुग्म के रूप में कार्य करता है x.

पूर्ण चतुर्भुज से

हार्मोनिक संयुग्म के लिए एक अन्य दृष्टिकोण एक पूर्ण चतुर्भुज की अवधारणा के माध्यम से है जैसे KLMN उपरोक्त आरेख में। चार बिंदुओं के आधार पर, पूर्ण चतुर्भुज में विपरीत भुजाओं और विकर्णों के जोड़े होते हैं। एच.एस.एम. कॉक्सेटर द्वारा हार्मोनिक संयुग्मों की अभिव्यक्ति में, विकर्णों को विपरीत पक्षों की एक जोड़ी माना जाता है:

D का हार्मोनिक संयुग्म है C इसके संबंध में A और B, जिसका अर्थ है कि एक चतुर्भुज है IJKL जैसे कि विपरीत भुजाओं का एक युग्म पर प्रतिच्छेद करता है A, और दूसरी जोड़ी at B, जबकि तीसरी जोड़ी मिलती है AB पर C और D.

यह कार्ल वॉन स्टॉड्ट था जिसने सबसे पहले हार्मोनिक संयुग्म का उपयोग मीट्रिक विचारों से स्वतंत्र प्रोजेक्टिव ज्यामिति के आधार के रूप में किया था:

...स्टौड प्रारंभिक ज्यामिति से प्रक्षेपी ज्यामिति को मुक्त करने में सफल रहा। उसके में Geometrie der Lage, स्टॉड ने एक पूर्ण चतुर्भुज या चतुर्भुज का उपयोग करते हुए विशुद्ध रूप से प्रक्षेपी मार्ग के बाद क्रॉस अनुपात की अवधारणा से स्वतंत्र रूप से तत्वों का एक हार्मोनिक चौगुना पेश किया।

1=D = M}
(ग्रीन M को नज़रअंदाज़ करें)।

मध्यबिंदु प्राप्त करने के लिए लागू पूर्ण चतुष्कोण को देखने के लिए, J. W. यंग से निम्नलिखित मार्ग पर विचार करें:

यदि दो मनमानी रेखाएँ AQ, AS के माध्यम से निकाले जाते हैं A और रेखाएँ BS, BQ के माध्यम से निकाले जाते हैं B इसके समानांतर AQ, AS क्रमशः, लाइनें AQ, SB परिभाषा के अनुसार, एक बिंदु पर मिलते हैं R अनंत पर, जबकि AS, QB परिभाषा के अनुसार एक बिंदु पर मिलते हैं P अनंत पर। पूर्ण चतुर्भुज PQRS पर दो विकर्ण बिंदु हैं A और B, जबकि विपरीत भुजाओं का शेष युग्म इससे होकर गुजरता है M और अनंत पर बिंदु AB. बिंदु M तब निर्माण द्वारा अनंत पर बिंदु का हार्मोनिक संयुग्म है AB इसके संबंध में A और B. दूसरी ओर, वह M खंड का मध्यबिंदु है AB परिचित प्रस्ताव से अनुसरण करता है कि समांतर चतुर्भुज के विकर्ण (PQRS) एक दूसरे को समद्विभाजित करें।

चतुर्धातुक संबंध

एक प्रोजेक्टिव रेंज पर चार ऑर्डर किए गए पॉइंट्स को हार्मोनिक पॉइंट्स कहा जाता है जब प्लेन में एक tetrastigm होता है जैसे कि पहले और तीसरे कोडॉट होते हैं और दूसरे दो पॉइंट तीसरे कोडॉट के कनेक्टर्स पर होते हैं। अगर p एक बिंदु है जो सीधे हार्मोनिक बिंदुओं के साथ नहीं है, के साथ जुड़ता है p अंक के साथ हार्मोनिक स्ट्रेट्स हैं। इसी तरह, यदि एक पेंसिल (गणित) की धुरी हार्मोनिक बिंदुओं के साथ सीधी रेखाएँ तिरछी है, तो बिंदुओं पर विमान हार्मोनिक विमान हैं।

इस प्रकार के संबंध में चार के समुच्चय को हार्मोनिक चौगुना कहा गया है।

प्रक्षेपी शंकु

प्रक्षेपी तल में एक शंकु एक वक्र है C जिसमें निम्न संपत्ति है: अगर P एक बिंदु पर नहीं है C, और यदि एक चर रेखा के माध्यम से P मिलते हैं C बिंदुओं पर A और B, तो के चर हार्मोनिक संयुग्म P इसके संबंध में A और B एक रेखा का पता लगाता है। बिंदु P को हार्मोनिक संयुग्मों की उस रेखा का ध्रुव कहा जाता है, और इस रेखा को ध्रुवीय रेखा कहा जाता है P शांकव के संबंध में। अधिक विवरण के लिए आलेख ध्रुव और ध्रुवीय देखें।

उलटा ज्यामिति

Main article: Inversive geometry

ऐसे मामले में जहां शंकु एक वृत्त है, वृत्त के विस्तारित व्यास पर, चक्र के संबंध में हार्मोनिक संयुग्मन उलटा ज्यामिति # एक वृत्त में उलटा होता है। यह तथ्य स्मोगोरज़ेव्स्की के प्रमेयों में से एक से आता है:

यदि हलकों k और q परस्पर ओर्थोगोनल हैं, तो के केंद्र से गुजरने वाली एक सीधी रेखा k और प्रतिच्छेदन q, के संबंध में सममित बिंदुओं पर ऐसा करता हैk.

यही है, अगर लाइन का एक विस्तारित व्यास है k, फिर चौराहों के साथ q हार्मोनिक संयुग्म हैं।

गैलोइस टेट्राड

गाल्वा क्षेत्र के ऊपर गैल्वा ज्यामिति में GF(q) एक रेखा है q + 1 अंक, जहां ∞ = (1,0). इस रेखा में चार बिंदु एक हार्मोनिक टेट्रैड बनाते हैं जब दो हार्मोनिक रूप से दूसरों को अलग करते हैं। स्थिति

$(c,d;a,b)=-1,\ {\text{ equivalently }}\ \ 2(cd+ab)=(c+d)(a+b),$

हार्मोनिक टेट्राड की विशेषता। इन चतुष्कोणों पर ध्यान देने से जीन डायडोने ने प्रक्षेपी रेखीय समूहों के कुछ आकस्मिक समरूपता के चित्रण के लिए नेतृत्व किया। PGL(2, q) के लिए q = 5, 7, 9. अगर q = 2ⁿ, और दिया A और B, फिर का हार्मोनिक संयुग्म C ही है।

पुनरावर्तित प्रक्षेप्य हार्मोनिक संयुग्म और सुनहरा अनुपात

होने देना P₀, P₁, P₂ वास्तविक प्रक्षेप्य रेखा पर तीन अलग-अलग बिंदु हों। बिंदुओं के अनंत क्रम पर विचार करें P_n, कहाँ P_n का हार्मोनिक संयुग्म है P_n-3 इसके संबंध में P_n-1, P_n-2 के लिए n > 2. यह क्रम अभिसारी है। एक सीमित सीमा के लिए P अपने पास

$\lim _{n\to \infty }{\frac {P_{n+1}P}{P_{n}P}}=\Phi -2=-\Phi ^{-2}=-{\frac {3-{\sqrt {5}}}{2}},$

कहाँ $\Phi ={\tfrac {1}{2}}(1+{\sqrt {5}})$ सुनहरा अनुपात है, अर्थात $P_{n+1}P\approx -\Phi ^{-2}P_{n}P$ बड़े के लिए n. हमारे पास एक अनंत सीमा के लिए है

$\lim _{n\to \infty }{\frac {P_{n+2}P_{n+1}}{P_{n+1}P_{n}}}=-1-\Phi =-\Phi ^{2}.$

सबूत के लिए प्रोजेक्टिव आइसोमोर्फिज्म पर विचार करें

$f(z)={\frac {az+b}{cz+d}}$ साथ

$f\left((-1)^{n}\Phi ^{2n}\right)=P_{n}.$

संदर्भ

• Juan Carlos Alverez (2000) Projective Geometry, see Chapter 2: The Real Projective Plane, section 3: Harmonic quadruples and von Staudt's theorem.
• Robert Lachlan (1893) An Elementary Treatise on Modern Pure Geometry, link from Cornell University Historical Math Monographs.
• Bertrand Russell (1903) Principles of Mathematics, page 384.
• Russell, John Wellesley (1905). Pure Geometry. Clarendon Press.