वर्णक्रमीय अनुक्रम

For the sorting of stars in astronomy, see Stellar classification.

होमोलॉजिकल बीजगणित और बीजगणितीय टोपोलॉजी में, वर्णक्रमीय अनुक्रम क्रमिक अनुमान लगाकर होमोलॉजी समूहों की गणना करने का एक साधन है। वर्णक्रमीय अनुक्रम सटीक अनुक्रमों का एक सामान्यीकरण है, और उनके परिचय के बाद से Jean Leray (1946a, 1946b), वे महत्वपूर्ण कम्प्यूटेशनल उपकरण बन गए हैं, विशेष रूप से बीजगणितीय टोपोलॉजी, बीजगणितीय ज्यामिति और होमोलॉजिकल बीजगणित में।

खोज और प्रेरणा

बीजगणितीय टोपोलॉजी में समस्याओं से प्रेरित होकर, जीन लेरे ने एक शीफ (गणित) की धारणा पेश की और खुद को शीफ कोहोलॉजी की गणना करने की समस्या का सामना करना पड़ा। शीफ़ कोहोमोलोजी की गणना करने के लिए, लेरे ने एक कम्प्यूटेशनल तकनीक पेश की जिसे अब लेरे वर्णक्रमीय अनुक्रम के रूप में जाना जाता है। इसने एक शीफ के सहसंबद्धता समूहों और एक शीफ की प्रत्यक्ष छवि के सहसंबद्धता समूहों के बीच एक संबंध दिया। इस संबंध में एक अनंत प्रक्रिया शामिल थी। लेरे ने पाया कि पुशफॉरवर्ड के कोहोमोलॉजी समूहों ने एक प्राकृतिक श्रृंखला परिसर का निर्माण किया, ताकि वह कोहोमोलॉजी के कोहोमोलॉजी को ले सकें। यह अभी भी मूल शीफ की सह-समरूपता नहीं थी, लेकिन एक अर्थ में यह एक कदम करीब थी। सह-समरूपता की सह-समरूपता ने फिर से एक श्रृंखला परिसर का निर्माण किया, और इसके सह-समरूपता ने एक श्रृंखला परिसर का निर्माण किया, इत्यादि। इस अनंत प्रक्रिया की सीमा मूलतः मूल शीफ के सहसंबद्धता समूहों के समान ही थी।

जल्द ही यह एहसास हुआ कि लेरे की कम्प्यूटेशनल तकनीक एक अधिक सामान्य घटना का उदाहरण थी। विभिन्न स्थितियों में वर्णक्रमीय अनुक्रम पाए गए, और उन्होंने कंपन जैसी ज्यामितीय स्थितियों और व्युत्पन्न फ़ैक्टर्स से जुड़े बीजगणितीय स्थितियों से आने वाले होमोलॉजी और कोहोमोलॉजी समूहों के बीच जटिल संबंध दिए। हालाँकि व्युत्पन्न श्रेणी की शुरुआत के बाद से उनका सैद्धांतिक महत्व कम हो गया है, फिर भी वे उपलब्ध सबसे प्रभावी कम्प्यूटेशनल उपकरण हैं। यह तब भी सत्य है जब वर्णक्रमीय अनुक्रम के कई पद गणना योग्य नहीं हैं।

दुर्भाग्य से, वर्णक्रमीय अनुक्रमों में बड़ी मात्रा में जानकारी ले जाने के कारण, उन्हें समझना मुश्किल है। यह जानकारी आम तौर पर एबेलियन समूहों या मॉड्यूल (गणित) के रैंक तीन जाली में निहित होती है। निपटने के लिए सबसे आसान मामले वे हैं जिनमें वर्णक्रमीय अनुक्रम अंततः ध्वस्त हो जाता है, जिसका अर्थ है कि अनुक्रम में आगे जाने से कोई नई जानकारी नहीं मिलती है। ऐसा न होने पर भी, विभिन्न तरकीबों द्वारा वर्णक्रमीय अनुक्रम से उपयोगी जानकारी प्राप्त करना अक्सर संभव होता है।

औपचारिक परिभाषा

कोहोमोलॉजिकल वर्णक्रमीय अनुक्रम

एक एबेलियन श्रेणी को ठीक करें, जैसे कि एक रिंग (गणित) पर मॉड्यूल (गणित) की एक श्रेणी, और एक गैर-नकारात्मक पूर्णांक $r_{0}$. एक कोहोमोलॉजिकल वर्णक्रमीय अनुक्रम एक अनुक्रम है $\{E_{r},d_{r}\}_{r\geq r_{0}}$ वस्तुओं का $E_{r}$ और एंडोमोर्फिज्म $d_{r}:E_{r}\to E_{r}$, ऐसा कि हर किसी के लिए $r\geq r_{0}$

1. $d_{r}\circ d_{r}=0$,
2. $E_{r+1}\cong H_{*}(E_{r},d_{r})$, होमोलॉजी (गणित) की $E_{r}$ इसके संबंध में $d_{r}$.

आमतौर पर समरूपताओं को दबा दिया जाता है और हम लिखते हैं $E_{r+1}=H_{*}(E_{r},d_{r})$ बजाय। एक वस्तु $E_{r}$ शीट कहा जाता है (जैसा कि कागज की शीट में), या कभी-कभी एक पृष्ठ या एक शब्द; एक एंडोमोर्फिज्म $d_{r}$ सीमा मानचित्र या विभेदक कहलाता है। कभी-कभी $E_{r+1}$ की व्युत्पन्न वस्तु कहलाती है $E_{r}$.

विग्रेडेड वर्णक्रमीय अनुक्रम

वास्तव में वर्णक्रमीय अनुक्रम अधिकतर एक रिंग (गणित) आर (या रिंगों के एक शीफ पर मॉड्यूल के दोगुने ग्रेडेड शीफ (गणित)) के ऊपर दोगुने श्रेणीबद्ध मॉड्यूल (गणित) की श्रेणी में होते हैं, यानी प्रत्येक शीट एक बड़ा ग्रेडेड आर-मॉड्यूल है ${\textstyle E_{r}=\bigoplus _{p,q\in \mathbb {Z} ^{2}}E_{r}^{p,q}.}$ तो इस मामले में एक कोहोमोलॉजिकल वर्णक्रमीय अनुक्रम एक अनुक्रम है $\{E_{r},d_{r}\}_{r\geq r_{0}}$ बिगग्रेडेड आर-मॉड्यूल का $\{E_{r}^{p,q}\}_{p,q}$ और प्रत्येक मॉड्यूल के लिए एंडोमोर्फिज्म का प्रत्यक्ष योग $d_{r}=(d_{r}^{p,q}:E_{r}^{p,q}\to E_{r}^{p+r,q-r+1})_{p,q\in \mathbb {Z} ^{2}}$ बाईडिग्री का $(r,1-r)$, ऐसा कि हर किसी के लिए $r\geq r_{0}$ यह मानता है कि:

1. $d_{r}^{p+r,q-r+1}\circ d_{r}^{p,q}=0$,
2. $E_{r+1}\cong H_{*}(E_{r},d_{r})$.

यहां प्रयुक्त अंकन को पूरक डिग्री कहा जाता है। कुछ लेखक लिखते हैं $E_{r}^{d,q}$ इसके बजाय, कहाँ $d=p+q$ कुल डिग्री है. वर्णक्रमीय अनुक्रम के आधार पर, पहली शीट पर सीमा मानचित्र में एक डिग्री हो सकती है जो r = 0, r = 1, या r = 2 से मेल खाती है। उदाहरण के लिए, नीचे वर्णित फ़िल्टर किए गए कॉम्प्लेक्स के वर्णक्रमीय अनुक्रम के लिए, r₀ = 0, लेकिन ग्रोथेंडिक वर्णक्रमीय अनुक्रम के लिए, आर₀ = 2. आमतौर पर आर₀ शून्य है, एक है, या दो है. ऊपर वर्णित अवर्गीकृत स्थिति में, आर₀ अप्रासंगिक है.

सजातीय वर्णक्रमीय अनुक्रम

अधिकतर जिन वस्तुओं के बारे में हम बात कर रहे हैं वे श्रृंखला जटिल हैं, जो अवरोही (ऊपर की तरह) या आरोही क्रम में होती हैं। बाद वाले मामले में, प्रतिस्थापित करके $E_{r}^{p,q}$ साथ $E_{p,q}^{r}$ और $d_{r}^{p,q}:E_{r}^{p,q}\to E_{r}^{p+r,q-r+1}$ साथ $d_{p,q}^{r}:E_{p,q}^{r}\to E_{p-r,q+r-1}^{r}$ (द्विडिग्री $(-r,r-1)$), किसी को कोहोमोलॉजिकल मामले के अनुरूप एक होमोलॉजिकल वर्णक्रमीय अनुक्रम की परिभाषा प्राप्त होती है।

एक श्रृंखला परिसर से वर्णक्रमीय अनुक्रम

अवर्गीकृत स्थिति में सबसे प्राथमिक उदाहरण एक श्रृंखला कॉम्प्लेक्स सी है_•. एक वस्तु सी_•श्रृंखला परिसरों की एबेलियन श्रेणी में स्वाभाविक रूप से एक अंतर डी के साथ आता है। चलो आर₀ = 0, और मान लीजिए E₀ सी हो_•. यह ई को मजबूर करता है₁ जटिल H(C) होना_•): i'वें स्थान पर यह C का i'वां होमोलॉजी समूह है_•. इस नए परिसर में एकमात्र प्राकृतिक अंतर शून्य मानचित्र है, इसलिए हमने d को छोड़ दिया₁ = 0. यह बल $E_{2}$ बराबर करने के लिए $E_{1}$, और फिर हमारा एकमात्र प्राकृतिक अंतर शून्य मानचित्र है। हमारी बाकी सभी शीटों पर शून्य अंतर डालने पर एक वर्णक्रमीय अनुक्रम मिलता है जिसके पद हैं:

• इ₀ = सी_•* और_r= एच(सी_•) सभी r ≥ 1 के लिए।

इस वर्णक्रमीय अनुक्रम की शर्तें पहली शीट पर स्थिर हो जाती हैं क्योंकि इसका एकमात्र गैर-तुच्छ अंतर शून्यवीं शीट पर था। परिणामस्वरूप, हमें बाद के चरणों में कोई और जानकारी नहीं मिल सकती है। आमतौर पर, बाद की शीटों से उपयोगी जानकारी प्राप्त करने के लिए, हमें अतिरिक्त संरचना की आवश्यकता होती है $E_{r}$.

विज़ुअलाइज़ेशन

ई₂ कोहॉमोलॉजिकल वर्णक्रमीय अनुक्रम की शीट

दोहरे श्रेणीबद्ध वर्णक्रमीय अनुक्रम में ट्रैक रखने के लिए भारी मात्रा में डेटा होता है, लेकिन एक सामान्य विज़ुअलाइज़ेशन तकनीक है जो वर्णक्रमीय अनुक्रम की संरचना को स्पष्ट करती है। हमारे पास तीन सूचकांक हैं, आर, पी, और क्यू। एक वस्तु $E_{r}$ के रूप में देखा जा सकता है $r^{th}$ किसी पुस्तक का चेकदार पृष्ठ। इन शीटों पर, हम p को क्षैतिज दिशा और q को ऊर्ध्वाधर दिशा मानेंगे। प्रत्येक जालक बिंदु पर हमारे पास वस्तु होती है $E_{r}^{p,q}$. अब अगले पन्ने की ओर मुड़ने का मतलब है होमोलॉजी लेना, यानी $(r+1)^{th}$ पेज इसका एक उपभाग है $r^{th}$ पृष्ठ। कुल डिग्री n = p + q प्रत्येक शीट पर तिरछे, उत्तर-पश्चिम से दक्षिण-पूर्व तक चलती है। समजात मामले में, अंतरों में द्विघात (-r, r − 1) होता है, इसलिए वे n को एक से कम करते हैं। कोहोमोलॉजिकल मामले में, n एक से बढ़ जाता है। अंतर r के संबंध में प्रत्येक मोड़ के साथ अपनी दिशा बदलते हैं।

कोहोमोलॉजिकल वर्णक्रमीय अनुक्रम के चार पृष्ठ

लाल तीर पहले चतुर्थांश अनुक्रम के मामले को प्रदर्शित करते हैं (उदाहरण वर्णक्रमीय अनुक्रम#प्रथम-चतुर्थांश शीट देखें), जहां केवल पहले चतुर्थांश की वस्तुएं गैर-शून्य हैं। पन्ने पलटते समय सभी विभेदों का डोमेन या कोडोमेन शून्य हो जाता है।

गुण

श्रेणीबद्ध गुण

कोहोमोलॉजिकल वर्णक्रमीय अनुक्रमों का सेट एक श्रेणी बनाता है: वर्णक्रमीय अनुक्रमों का एक रूपवाद $f:E\to E'$ परिभाषा के अनुसार मानचित्रों का एक संग्रह है $f_{r}:E_{r}\to E'_{r}$ जो विभेदकों के साथ संगत हैं, यानी $f_{r}\circ d_{r}=d'_{r}\circ f_{r}$, और क्रमशः rवें चरण की सह-समरूपता और E और E' की (r+1)वीं शीट के बीच दिए गए समरूपता के साथ: $f_{r+1}(E_{r+1})\,=\,f_{r+1}(H(E_{r}))\,=\,H(f_{r}(E_{r}))$. बड़े ग्रेड वाले मामले में, उन्हें ग्रेजुएशन का भी सम्मान करना चाहिए: $f_{r}(E_{r}^{p,q})\subset {E'_{r}}^{p,q}.$

गुणात्मक संरचना

एक कप उत्पाद एक कोहोमोलॉजी समूह को एक रिंग (गणित) देता है, इसे एक कोहोमोलोजी रिंग में बदल देता है। इस प्रकार, वलय संरचना के साथ वर्णक्रमीय अनुक्रम पर भी विचार करना स्वाभाविक है। होने देना $E_{r}^{p,q}$ कोहोमोलॉजिकल प्रकार का एक वर्णक्रमीय अनुक्रम बनें। हम कहते हैं कि इसकी गुणात्मक संरचना है यदि (i) $E_{r}$ (दोगुने श्रेणीबद्ध) विभेदक श्रेणीबद्ध बीजगणित और (ii) गुणन हैं $E_{r+1}$ उस पर प्रेरित है $E_{r}$ कोहोमोलॉजी के मार्ग के माध्यम से।

एक विशिष्ट उदाहरण फाइब्रेशन के लिए कोहोमोलॉजिकल सेरे वर्णक्रमीय अनुक्रम है $F\to E\to B$, जब गुणांक समूह एक रिंग आर होता है। इसमें फाइबर के कप उत्पादों और आधार पर प्रेरित गुणक संरचना होती है $E_{2}$-पृष्ठ। हालाँकि, सामान्य तौर पर सीमित अवधि $E_{\infty }$ H(E; R) के श्रेणीबद्ध बीजगणित के रूप में समरूपी नहीं है। अनुक्रम पर अंतर की गणना के लिए गुणक संरचना बहुत उपयोगी हो सकती है।

वर्णक्रमीय अनुक्रमों का निर्माण

वर्णक्रमीय अनुक्रमों का निर्माण विभिन्न तरीकों से किया जा सकता है। बीजगणितीय टोपोलॉजी में, सटीक युग्म शायद निर्माण के लिए सबसे आम उपकरण है। बीजगणितीय ज्यामिति में, वर्णक्रमीय अनुक्रम आमतौर पर कोचेन परिसरों के निस्पंदन से निर्मित होते हैं।

एक सटीक जोड़े का वर्णक्रमीय अनुक्रम

Main article: Exact couple

वर्णक्रमीय अनुक्रमों के निर्माण की एक अन्य तकनीक विलियम शूमाकर मैसी की सटीक युग्मों की विधि है। बीजगणितीय टोपोलॉजी में सटीक जोड़े विशेष रूप से आम हैं। इसके बावजूद वे अमूर्त बीजगणित में अलोकप्रिय हैं, जहां अधिकांश वर्णक्रमीय अनुक्रम फ़िल्टर किए गए परिसरों से आते हैं।

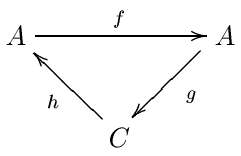
सटीक जोड़ों को परिभाषित करने के लिए, हम फिर से एबेलियन श्रेणी से शुरू करते हैं। पहले की तरह, व्यवहार में यह आमतौर पर एक रिंग के ऊपर दोगुने श्रेणीबद्ध मॉड्यूल की श्रेणी होती है। एक सटीक युग्म वस्तुओं (ए, सी) की एक जोड़ी है, साथ ही इन वस्तुओं के बीच तीन समरूपताएँ होती हैं: एफ : ए → ए, जी : ए → सी और एच : सी → ए कुछ सटीक शर्तों के अधीन:

• छवि (गणित) एफ = कर्नेल (बीजगणित) जी
• छवि जी = कर्नेल एच
• छवि एच = कर्नेल एफ

हम इस डेटा को (ए, सी, एफ, जी, एच) द्वारा संक्षिप्त करेंगे। सटीक जोड़ों को आमतौर पर त्रिकोण के रूप में दर्शाया जाता है। हम देखेंगे कि C E से मेल खाता है₀ वर्णक्रमीय अनुक्रम का पद और वह A कुछ सहायक डेटा है।

वर्णक्रमीय अनुक्रम की अगली शीट पर जाने के लिए, हम 'व्युत्पन्न युग्म' बनाएंगे। हमलोग तैयार हैं:

• डी = जी o एच
• ए<नोविकी>'</नोविकी> = एफ(ए)
• C' = Ker d / Im d
• f' = f|_A', f से A' तक का प्रतिबंध
• h' : C' → A' h से प्रेरित है। यह देखना सीधा है कि एच ऐसे मानचित्र को प्रेरित करता है।
• g' : A' → C' को तत्वों पर इस प्रकार परिभाषित किया गया है: A' में प्रत्येक a के लिए , A में कुछ b के लिए a को f(b) के रूप में लिखें। g'(a) को C' में g(b) की छवि के रूप में परिभाषित किया गया है। सामान्य तौर पर, एबेलियन श्रेणियों के लिए एम्बेडिंग प्रमेयों में से एक का उपयोग करके g' का निर्माण किया जा सकता है।

यहां से यह जांचना आसान है कि (A', C', f', g', h ') एक सटीक जोड़ा है। C' E से मेल खाता है₁वर्णक्रमीय अनुक्रम की अवधि. हम सटीक जोड़े (ए) प्राप्त करने के लिए इस प्रक्रिया को दोहरा सकते हैं^(एन), सी^(एन), एफ^(एन), जी^(एन), ज^(एन)).

वर्णक्रमीय अनुक्रम बनाने के लिए, मान लीजिए E_nसी हो^(एन)और डी_nनिवेदन करना^(एन) o h^(एन).

इस विधि से निर्मित वर्णक्रमीय अनुक्रम

• सेरे वर्णक्रमीय अनुक्रम - एक तंतु की समरूपता (सह) की गणना करने के लिए उपयोग किया जाता है
• अतियाह-हिर्ज़ेब्रुक वर्णक्रमीय अनुक्रम - के-सिद्धांत जैसे असाधारण सह-समरूपता सिद्धांतों की (सह) समरूपता की गणना करने के लिए उपयोग किया जाता है
• बॉकस्टीन वर्णक्रमीय अनुक्रम।
• फ़िल्टर किए गए परिसरों के वर्णक्रमीय अनुक्रम

फ़िल्टर किए गए कॉम्प्लेक्स का वर्णक्रमीय अनुक्रम

एक बहुत ही सामान्य प्रकार का वर्णक्रमीय अनुक्रम निस्पंदन (अमूर्त बीजगणित) कोचेन कॉम्प्लेक्स से आता है, क्योंकि यह स्वाभाविक रूप से एक बड़े पैमाने पर वस्तु को प्रेरित करता है। एक कोचेन कॉम्प्लेक्स पर विचार करें $(C^{\bullet },d)$ अवरोही निस्पंदन के साथ, ${\textstyle ...\supset \,F^{-2}C^{\bullet }\,\supset \,F^{-1}C^{\bullet }\supset F^{0}C^{\bullet }\,\supset \,F^{1}C^{\bullet }\,\supset \,F^{2}C^{\bullet }\,\supset \,F^{3}C^{\bullet }\,\supset ...\,}$ . हमें आवश्यकता है कि सीमा मानचित्र निस्पंदन के साथ संगत हो, अर्थात। ${\textstyle d(F^{p}C^{n})\subset F^{p}C^{n+1}}$, और यह कि निस्पंदन संपूर्ण है, अर्थात, सभी के सेट का मिलन ${\textstyle F^{p}C^{\bullet }}$ संपूर्ण श्रृंखला परिसर है ${\textstyle C^{\bullet }}$. फिर वहाँ एक वर्णक्रमीय अनुक्रम मौजूद है ${\textstyle E_{0}^{p,q}=F^{p}C^{p+q}/F^{p+1}C^{p+q}}$ और ${\textstyle E_{1}^{p,q}=H^{p+q}(F^{p}C^{\bullet }/F^{p+1}C^{\bullet })}$. बाद में, हम यह भी मान लेंगे कि निस्पंदन हॉसडॉर्फ या अलग है, अर्थात, सभी के सेट का प्रतिच्छेदन ${\textstyle F^{p}C^{\bullet }}$ शून्य है.

निस्पंदन उपयोगी है क्योंकि यह शून्य से निकटता का माप देता है: जैसे-जैसे पी बढ़ता है, ${\textstyle F^{p}C^{\bullet }}$ शून्य के करीब और करीब आता जाता है। हम इस निस्पंदन से एक वर्णक्रमीय अनुक्रम का निर्माण करेंगे जहां बाद की शीटों में सह-सीमाएं और सह-चक्र मूल परिसर में सह-सीमाओं और सह-चक्रों के करीब और करीब आते जाएंगे। इस वर्णक्रमीय अनुक्रम को निस्पंदन डिग्री पी और पूरक डिग्री द्वारा दोगुना वर्गीकृत किया गया है q = n − p.

निर्माण

$C^{\bullet }$ इसमें केवल एक ही ग्रेडिंग और एक निस्पंदन है, इसलिए हम पहले वर्णक्रमीय अनुक्रम के पहले पृष्ठ के लिए एक दोगुनी श्रेणी वाली वस्तु का निर्माण करते हैं। दूसरी ग्रेडिंग प्राप्त करने के लिए, हम निस्पंदन के संबंध में संबंधित ग्रेडेड ऑब्जेक्ट लेंगे। हम इसे असामान्य तरीके से लिखेंगे जो उचित होगा $E_{1}$ कदम:

$Z_{-1}^{p,q}=Z_{0}^{p,q}=F^{p}C^{p+q}$

$B_{0}^{p,q}=0$

$E_{0}^{p,q}={\frac {Z_{0}^{p,q}}{B_{0}^{p,q}+Z_{-1}^{p+1,q-1}}}={\frac {F^{p}C^{p+q}}{F^{p+1}C^{p+q}}}$

$E_{0}=\bigoplus _{p,q\in \mathbf {Z} }E_{0}^{p,q}$

चूँकि हमने मान लिया था कि सीमा मानचित्र निस्पंदन के अनुकूल था, $E_{0}$ एक दोगुनी श्रेणीकृत वस्तु है और एक प्राकृतिक दोगुना श्रेणीबद्ध सीमा मानचित्र है $d_{0}$ पर $E_{0}$. पाने के $E_{1}$, हम होमोलॉजी लेते हैं $E_{0}$.

${\bar {Z}}_{1}^{p,q}=\ker d_{0}^{p,q}:E_{0}^{p,q}\rightarrow E_{0}^{p,q+1}=\ker d_{0}^{p,q}:F^{p}C^{p+q}/F^{p+1}C^{p+q}\rightarrow F^{p}C^{p+q+1}/F^{p+1}C^{p+q+1}$

${\bar {B}}_{1}^{p,q}={\mbox{im }}d_{0}^{p,q-1}:E_{0}^{p,q-1}\rightarrow E_{0}^{p,q}={\mbox{im }}d_{0}^{p,q-1}:F^{p}C^{p+q-1}/F^{p+1}C^{p+q-1}\rightarrow F^{p}C^{p+q}/F^{p+1}C^{p+q}$

$E_{1}^{p,q}={\frac {{\bar {Z}}_{1}^{p,q}}{{\bar {B}}_{1}^{p,q}}}={\frac {\ker d_{0}^{p,q}:E_{0}^{p,q}\rightarrow E_{0}^{p,q+1}}{{\mbox{im }}d_{0}^{p,q-1}:E_{0}^{p,q-1}\rightarrow E_{0}^{p,q}}}$

$E_{1}=\bigoplus _{p,q\in \mathbf {Z} }E_{1}^{p,q}=\bigoplus _{p,q\in \mathbf {Z} }{\frac {{\bar {Z}}_{1}^{p,q}}{{\bar {B}}_{1}^{p,q}}}$

नोटिस जो ${\bar {Z}}_{1}^{p,q}$ और ${\bar {B}}_{1}^{p,q}$ में चित्रों के रूप में लिखा जा सकता है $E_{0}^{p,q}$ का

$Z_{1}^{p,q}=\ker d_{0}^{p,q}:F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+1}C^{p+q+1}$

$B_{1}^{p,q}=({\mbox{im }}d_{0}^{p,q-1}:F^{p}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}$

और वह हमारे पास है

$E_{1}^{p,q}={\frac {Z_{1}^{p,q}}{B_{1}^{p,q}+Z_{0}^{p+1,q-1}}}.$

$Z_{1}^{p,q}$ वास्तव में वे तत्व हैं जिन्हें अंतर निस्पंदन में एक स्तर ऊपर धकेलता है, और $B_{1}^{p,q}$ बिल्कुल उन तत्वों की छवि है जो अंतर निस्पंदन में शून्य स्तर तक बढ़ाता है। इससे पता चलता है कि हमें चुनना चाहिए $Z_{r}^{p,q}$ ऐसे तत्व होने के लिए जो अंतर निस्पंदन में आर स्तर को ऊपर धकेलता है $B_{r}^{p,q}$ उन तत्वों की छवि होना जो अंतर निस्पंदन में r-1 स्तर को ऊपर धकेलता है। दूसरे शब्दों में, वर्णक्रमीय अनुक्रम को संतुष्ट करना चाहिए

$Z_{r}^{p,q}=\ker d_{0}^{p,q}:F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+r}C^{p+q+1}$

$B_{r}^{p,q}=({\mbox{im }}d_{0}^{p-r+1,q+r-2}:F^{p-r+1}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}$

$E_{r}^{p,q}={\frac {Z_{r}^{p,q}}{B_{r}^{p,q}+Z_{r-1}^{p+1,q-1}}}$

और हमें रिश्ता निभाना चाहिए

$B_{r}^{p,q}=d_{0}^{p,q}(Z_{r-1}^{p-r+1,q+r-2}).$

इसे समझने के लिए, हमें एक अंतर खोजना होगा $d_{r}$ सभी के ऊपर $E_{r}$ और सत्यापित करें कि यह होमोलॉजी आइसोमोर्फिक की ओर ले जाता है $E_{r+1}$. अंतर

$d_{r}^{p,q}:E_{r}^{p,q}\rightarrow E_{r}^{p+r,q-r+1}$

मूल अंतर को सीमित करके परिभाषित किया गया है $d$ पर परिभाषित $C^{p+q}$ उपविषय के लिए $Z_{r}^{p,q}$. यह जांचना सीधा है कि की समरूपता $E_{r}$ इस अंतर के संबंध में है $E_{r+1}$, तो यह एक वर्णक्रमीय अनुक्रम देता है। दुर्भाग्य से, अंतर बहुत स्पष्ट नहीं है। वर्णक्रमीय अनुक्रम को सफलतापूर्वक लागू करने के लिए अंतरों को निर्धारित करना या उनके आसपास काम करने के तरीके खोजना मुख्य चुनौतियों में से एक है।

इस विधि से निर्मित वर्णक्रमीय अनुक्रम

• हॉज-डी राम वर्णक्रमीय अनुक्रम
• दोहरे परिसर का वर्णक्रमीय अनुक्रम
• मिश्रित हॉज संरचनाओं के निर्माण के लिए उपयोग किया जा सकता है

दोहरे परिसर का वर्णक्रमीय अनुक्रम

एक अन्य सामान्य वर्णक्रमीय अनुक्रम दोहरे परिसर का वर्णक्रमीय अनुक्रम है। एक डबल कॉम्प्लेक्स वस्तुओं का एक संग्रह है सी_i,jसभी पूर्णांकों i और j के लिए दो अंतरों के साथ, d ^मैंऔर डी ^{द्वितीय}. डी ^Iको i, और d को कम करने के लिए माना जाता है ^II को j में कमी माना गया है। इसके अलावा, हम मानते हैं कि अंतर एंटीकम्यूट हैं, ताकि डी ^मैंd ^II+d ^IId ^I = 0. हमारा लक्ष्य पुनरावृत्त समरूपताओं की तुलना करना है $H_{i}^{I}(H_{j}^{II}(C_{\bullet ,\bullet }))$ और $H_{j}^{II}(H_{i}^{I}(C_{\bullet ,\bullet }))$. हम अपने दोहरे कॉम्प्लेक्स को दो अलग-अलग तरीकों से फ़िल्टर करके ऐसा करेंगे। यहां हमारे फ़िल्टरेशन हैं:

$(C_{i,j}^{I})_{p}={\begin{cases}0&{\text{if }}i<p\\C_{i,j}&{\text{if }}i\geq p\end{cases}}$

$(C_{i,j}^{II})_{p}={\begin{cases}0&{\text{if }}j<p\\C_{i,j}&{\text{if }}j\geq p\end{cases}}$

वर्णक्रमीय अनुक्रम प्राप्त करने के लिए, हम पिछले उदाहरण पर विचार करेंगे। हम कुल कॉम्प्लेक्स टी(सी) को परिभाषित करते हैं_•,•) वह सम्मिश्र होना जिसका n'वाँ पद है $\bigoplus _{i+j=n}C_{i,j}$ और जिसका अंतर d है ^मैं+d ^{द्वितीय}. यह एक जटिल है क्योंकि d ^मैंऔर डी ^IIएंटीकम्यूटिंग अंतर हैं। सी पर दो निस्पंदन_i,jकुल परिसर पर दो फ़िल्टरेशन दें:

$T_{n}(C_{\bullet ,\bullet })_{p}^{I}=\bigoplus _{i+j=n \atop i>p-1}C_{i,j}$

$T_{n}(C_{\bullet ,\bullet })_{p}^{II}=\bigoplus _{i+j=n \atop j>p-1}C_{i,j}$

यह दिखाने के लिए कि ये वर्णक्रमीय अनुक्रम पुनरावृत्त समरूपताओं के बारे में जानकारी देते हैं, हम ई पर काम करेंगे⁰, ई¹, और ई²टी(सी) पर आई निस्पंदन की शर्तें_•,•). ई⁰शब्द स्पष्ट है:

${}^{I}E_{p,q}^{0}=T_{n}(C_{\bullet ,\bullet })_{p}^{I}/T_{n}(C_{\bullet ,\bullet })_{p+1}^{I}=\bigoplus _{i+j=n \atop i>p-1}C_{i,j}{\Big /}\bigoplus _{i+j=n \atop i>p}C_{i,j}=C_{p,q},$

कहाँ n = p + q.

ई को खोजने के लिए¹शब्द, हमें d निर्धारित करने की आवश्यकता है ^मैं+d ^{ई पर द्वितीय0. ध्यान दें कि n के संबंध में अंतर की डिग्री −1 होनी चाहिए, इसलिए हमें एक नक्शा मिलता है}

$d_{p,q}^{I}+d_{p,q}^{II}:T_{n}(C_{\bullet ,\bullet })_{p}^{I}/T_{n}(C_{\bullet ,\bullet })_{p+1}^{I}=C_{p,q}\rightarrow T_{n-1}(C_{\bullet ,\bullet })_{p}^{I}/T_{n-1}(C_{\bullet ,\bullet })_{p+1}^{I}=C_{p,q-1}$

नतीजतन, ई पर अंतर⁰मानचित्र C है_p,q → सी_p,q−1 डी द्वारा प्रेरित ^मैं+d ^{द्वितीय}. लेकिन डी ^{मेरे पास ऐसा नक्शा तैयार करने के लिए गलत डिग्री है, इसलिए डी मुझे E पर शून्य होना चाहिए0. इसका मतलब है कि अंतर बिल्कुल d है II, तो हमें मिलता है}

${}^{I}E_{p,q}^{1}=H_{q}^{II}(C_{p,\bullet }).$

ई को खोजने के लिए², हमें यह निर्धारित करने की आवश्यकता है

$d_{p,q}^{I}+d_{p,q}^{II}:H_{q}^{II}(C_{p,\bullet })\rightarrow H_{q}^{II}(C_{p+1,\bullet })$

क्योंकि ई¹डी के संबंध में बिलकुल समरूपता थी ^{द्वितीय}, डी ^IIE पर शून्य है¹. परिणामस्वरूप, हमें मिलता है

${}^{I}E_{p,q}^{2}=H_{p}^{I}(H_{q}^{II}(C_{\bullet ,\bullet })).$

अन्य निस्पंदन का उपयोग करने से हमें समान ई के साथ एक अलग वर्णक्रमीय अनुक्रम मिलता है²शब्द:

${}^{II}E_{p,q}^{2}=H_{q}^{II}(H_{p}^{I}(C_{\bullet ,\bullet })).$

इन दो वर्णक्रमीय अनुक्रमों के बीच संबंध ढूंढना बाकी है। यह पता चलेगा कि जैसे-जैसे r बढ़ता है, दोनों अनुक्रम उपयोगी तुलना की अनुमति देने के लिए पर्याप्त समान हो जाएंगे।

अभिसरण, पतन, और समापन

चक्रों और सीमाओं के निस्पंदन के रूप में व्याख्या

चलो ई_r एक वर्णक्रमीय अनुक्रम बनें, मान लीजिए r = 1 से शुरू करें। फिर उप-वस्तुओं का एक क्रम होता है

$0=B_{0}\subset B_{1}\subset B_{2}\subset \dots \subset B_{r}\subset \dots \subset Z_{r}\subset \dots \subset Z_{2}\subset Z_{1}\subset Z_{0}=E_{1}$

ऐसा है कि $E_{r}\simeq Z_{r-1}/B_{r-1}$; वास्तव में, पुनरावर्ती रूप से हम जाने देते हैं $Z_{0}=E_{1},B_{0}=0$ और जाने $Z_{r},B_{r}$ ऐसा हो $Z_{r}/B_{r-1},B_{r}/B_{r-1}$ की गिरी और छवि हैं $E_{r}{\overset {d_{r}}{\to }}E_{r}.$ फिर हमने जाने दिया $Z_{\infty }=\cap _{r}Z_{r},B_{\infty }=\cup _{r}B_{r}$ और

$E_{\infty }=Z_{\infty }/B_{\infty }$;

इसे सीमित शब्द कहा जाता है। (बेशक, ऐसे $E_{\infty }$ श्रेणी में मौजूद होने की आवश्यकता नहीं है, लेकिन यह आमतौर पर एक गैर-मुद्दा है क्योंकि उदाहरण के लिए मॉड्यूल की श्रेणी में ऐसी सीमाएं मौजूद हैं या चूंकि व्यवहार में जिस वर्णक्रमीय अनुक्रम के साथ कोई काम करता है वह ख़राब हो जाता है; उपरोक्त अनुक्रम में केवल सीमित संख्या में ही समावेशन हैं।)

अभिसरण की शर्तें

हम कहते हैं कि यदि कोई श्रेणीबद्ध वस्तु है तो वर्णक्रमीय अनुक्रम कमजोर रूप से परिवर्तित होता है $H^{\bullet }$ एक निस्पंदन के साथ $F^{\bullet }H^{n}$ हरएक के लिए $n$, और हर किसी के लिए $p$ वहाँ एक समरूपता मौजूद है $E_{\infty }^{p,q}\cong F^{p}H^{p+q}/F^{p+1}H^{p+q}$. यह एकत्रित हो जाता है $H^{\bullet }$ यदि निस्पंदन $F^{\bullet }H^{n}$ हॉसडॉर्फ है, अर्थात्। $\cap _{p}F^{p}C^{\bullet }=0$. हम लिखते हैं

$E_{r}^{p,q}\Rightarrow _{p}E_{\infty }^{n}$

इसका अर्थ यह है कि जब भी p + q = n, $E_{r}^{p,q}$ में एकत्रित हो जाता है $E_{\infty }^{p,q}$. हम कहते हैं कि एक वर्णक्रमीय अनुक्रम $E_{r}^{p,q}$ से सटा हुआ है $E_{\infty }^{p,q}$ यदि प्रत्येक के लिए $p,q$ वहाँ है $r(p,q)$ ऐसा कि सभी के लिए $r\geq r(p,q)$, $E_{r}^{p,q}=E_{r(p,q)}^{p,q}$. तब $E_{r(p,q)}^{p,q}=E_{\infty }^{p,q}$ सीमित शब्द है. वर्णक्रमीय अनुक्रम नियमित या पतित होता है $r_{0}$ यदि अंतर $d_{r}^{p,q}$ सभी के लिए शून्य हैं $r\geq r_{0}$. यदि विशेष रूप से वहाँ है $r_{0}\geq 2$, ऐसे कि $r_{0}^{th}$ शीट एक पंक्ति या एक कॉलम पर केंद्रित है, तो हम कहते हैं कि यह ढह जाती है। प्रतीकों में हम लिखते हैं:

$E_{r}^{p,q}\Rightarrow _{p}E_{\infty }^{p,q}$

पी निस्पंदन सूचकांक को इंगित करता है। लिखना बहुत आम बात है $E_{2}^{p,q}$ एब्यूमेंट के बाईं ओर शब्द, क्योंकि यह अधिकांश वर्णक्रमीय अनुक्रमों में सबसे उपयोगी शब्द है। अनफ़िल्टर्ड चेन कॉम्प्लेक्स का वर्णक्रमीय अनुक्रम पहली शीट पर ख़राब हो जाता है (पहला उदाहरण देखें): चूँकि शून्य शीट के बाद कुछ भी नहीं होता है, सीमित शीट $E_{\infty }$ वैसा ही है जैसा कि $E_{1}$.

वर्णक्रमीय अनुक्रम का पांच-अवधि वाला सटीक अनुक्रम कुछ निम्न-डिग्री शर्तों और ई से संबंधित है_∞ शर्तें।

अध:पतन के उदाहरण

फ़िल्टर किए गए कॉम्प्लेक्स का वर्णक्रमीय अनुक्रम, जारी

ध्यान दें कि हमारे पास समावेशन की एक श्रृंखला है:

$Z_{0}^{p,q}\supseteq Z_{1}^{p,q}\supseteq Z_{2}^{p,q}\supseteq \cdots \supseteq B_{2}^{p,q}\supseteq B_{1}^{p,q}\supseteq B_{0}^{p,q}$

हम पूछ सकते हैं कि परिभाषित करने से क्या होता है

$Z_{\infty }^{p,q}=\bigcap _{r=0}^{\infty }Z_{r}^{p,q},$

$B_{\infty }^{p,q}=\bigcup _{r=0}^{\infty }B_{r}^{p,q},$

$E_{\infty }^{p,q}={\frac {Z_{\infty }^{p,q}}{B_{\infty }^{p,q}+Z_{\infty }^{p+1,q-1}}}.$

$E_{\infty }^{p,q}$ इस वर्णक्रमीय अनुक्रम के समर्थन के लिए एक स्वाभाविक उम्मीदवार है। अभिसरण स्वचालित नहीं है, लेकिन कई मामलों में होता है। विशेष रूप से, यदि निस्पंदन परिमित है और इसमें बिल्कुल r गैर-तुच्छ चरण शामिल हैं, तो rth शीट के बाद वर्णक्रमीय अनुक्रम ख़राब हो जाता है। अभिसरण तब भी होता है जब कॉम्प्लेक्स और निस्पंदन दोनों नीचे से घिरे होते हैं या दोनों ऊपर से बंधे होते हैं।

हमारे वर्णक्रमीय अनुक्रम के संबंध का अधिक विस्तार से वर्णन करने के लिए, ध्यान दें कि हमारे पास सूत्र हैं:

$Z_{\infty }^{p,q}=\bigcap _{r=0}^{\infty }Z_{r}^{p,q}=\bigcap _{r=0}^{\infty }\ker(F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+r}C^{p+q+1})$

$B_{\infty }^{p,q}=\bigcup _{r=0}^{\infty }B_{r}^{p,q}=\bigcup _{r=0}^{\infty }({\mbox{im }}d^{p,q-r}:F^{p-r}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}$

यह देखने के लिए कि इसका क्या मतलब है $Z_{\infty }^{p,q}$ याद रखें कि हमने मान लिया था कि निस्पंदन अलग हो गया था। इसका तात्पर्य यह है कि जैसे-जैसे r बढ़ता है, गुठली सिकुड़ती जाती है, जब तक कि हमारे पास शेष न रह जाए $Z_{\infty }^{p,q}=\ker(F^{p}C^{p+q}\rightarrow C^{p+q+1})$. के लिए $B_{\infty }^{p,q}$, याद रखें कि हमने मान लिया था कि निस्पंदन संपूर्ण था। इसका तात्पर्य यह है कि जैसे-जैसे r बढ़ता है, छवियाँ हमारे पहुँचने तक बढ़ती हैं $B_{\infty }^{p,q}={\text{im }}(C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}$. हम निष्कर्ष निकालते हैं

$E_{\infty }^{p,q}={\mbox{gr}}_{p}H^{p+q}(C^{\bullet })$,

अर्थात्, वर्णक्रमीय अनुक्रम का समापन सी के (p+q)वें समरूपता का pth श्रेणीबद्ध भाग है। यदि हमारा वर्णक्रमीय अनुक्रम अभिसरण करता है, तो हम निष्कर्ष निकालते हैं कि:

$E_{r}^{p,q}\Rightarrow _{p}H^{p+q}(C^{\bullet })$

लंबे सटीक अनुक्रम

फ़िल्टर किए गए कॉम्प्लेक्स के वर्णक्रमीय अनुक्रम का उपयोग करके, हम लंबे सटीक अनुक्रमों के अस्तित्व को प्राप्त कर सकते हैं। कोचेन कॉम्प्लेक्स 0 → ए का संक्षिप्त सटीक अनुक्रम चुनें^• → बी^• → सी^• → 0, और पहले मानचित्र को कॉल करें f^• : ए^• → बी^•. हमें होमोलॉजी ऑब्जेक्ट्स एच के प्राकृतिक मानचित्र मिलते हैं^एन(ए^•) → एच^एन(बी^•) → एच^एन(सी^•), और हम जानते हैं कि यह बिल्कुल मध्य में है। हम कनेक्टिंग होमोमोर्फिज्म को खोजने और यह साबित करने के लिए फ़िल्टर किए गए कॉम्प्लेक्स के वर्णक्रमीय अनुक्रम का उपयोग करेंगे कि परिणामी अनुक्रम सटीक है। शुरू करने के लिए, हम बी को फ़िल्टर करते हैं^•:

$F^{0}B^{n}=B^{n}$

$F^{1}B^{n}=A^{n}$

$F^{2}B^{n}=0$

यह देता है:

$E_{0}^{p,q}={\frac {F^{p}B^{p+q}}{F^{p+1}B^{p+q}}}={\begin{cases}0&{\text{if }}p<0{\text{ or }}p>1\\C^{q}&{\text{if }}p=0\\A^{q+1}&{\text{if }}p=1\end{cases}}$

$E_{1}^{p,q}={\begin{cases}0&{\text{if }}p<0{\text{ or }}p>1\\H^{q}(C^{\bullet })&{\text{if }}p=0\\H^{q+1}(A^{\bullet })&{\text{if }}p=1\end{cases}}$

अंतर में द्विपक्षीय (1, 0) है, इसलिए डी_0,q: एच^प्र(सी^•) → एच^q+1(ए^•). ये साँप लेम्मा से जुड़ने वाली समरूपताएं हैं, और मानचित्र ए के साथ^• → बी^• → सी^•, वे एक क्रम देते हैं:

$\cdots \rightarrow H^{q}(B^{\bullet })\rightarrow H^{q}(C^{\bullet })\rightarrow H^{q+1}(A^{\bullet })\rightarrow H^{q+1}(B^{\bullet })\rightarrow \cdots$

यह दिखाना बाकी है कि यह क्रम ए और सी स्थानों पर सटीक है। ध्यान दें कि यह वर्णक्रमीय अनुक्रम E पर ख़राब हो जाता है₂ पद क्योंकि अंतरों में द्विडिग्री (2, −1) होती है। नतीजतन, ई₂ पद E के समान है_∞ अवधि:

$E_{2}^{p,q}\cong {\text{gr}}_{p}H^{p+q}(B^{\bullet })={\begin{cases}0&{\text{if }}p<0{\text{ or }}p>1\\H^{q}(B^{\bullet })/H^{q}(A^{\bullet })&{\text{if }}p=0\\{\text{im }}H^{q+1}f^{\bullet }:H^{q+1}(A^{\bullet })\rightarrow H^{q+1}(B^{\bullet })&{\text{if }}p=1\end{cases}}$

लेकिन हमारे पास ई का प्रत्यक्ष विवरण भी है₂ ई की समरूपता के रूप में शब्द₁ अवधि। ये दो विवरण समरूपी होने चाहिए:

$H^{q}(B^{\bullet })/H^{q}(A^{\bullet })\cong \ker d_{0,q}^{1}:H^{q}(C^{\bullet })\rightarrow H^{q+1}(A^{\bullet })$

${\text{im }}H^{q+1}f^{\bullet }:H^{q+1}(A^{\bullet })\rightarrow H^{q+1}(B^{\bullet })\cong H^{q+1}(A^{\bullet })/({\mbox{im }}d_{0,q}^{1}:H^{q}(C^{\bullet })\rightarrow H^{q+1}(A^{\bullet }))$

पहला सी स्थान पर सटीकता देता है, और दूसरा ए स्थान पर सटीकता देता है।

दोहरे परिसर का वर्णक्रमीय अनुक्रम, जारी

फ़िल्टर किए गए कॉम्प्लेक्स के लिए एब्यूमेंट का उपयोग करते हुए, हम पाते हैं कि:

$H_{p}^{I}(H_{q}^{II}(C_{\bullet ,\bullet }))\Rightarrow _{p}H^{p+q}(T(C_{\bullet ,\bullet }))$

$H_{q}^{II}(H_{p}^{I}(C_{\bullet ,\bullet }))\Rightarrow _{q}H^{p+q}(T(C_{\bullet ,\bullet }))$

सामान्य तौर पर, एच पर दो ग्रेडिंग^p+q(T(C_•,•)) विशिष्ट हैं. इसके बावजूद, इन दो वर्णक्रमीय अनुक्रमों से उपयोगी जानकारी प्राप्त करना अभी भी संभव है।

टोर की क्रमविनिमेयता

मान लीजिए R एक रिंग है, मान लीजिए M एक दायां R-मॉड्यूल है और N एक बायां R-मॉड्यूल है। याद रखें कि टेंसर उत्पाद के व्युत्पन्न फ़ैक्टर को टोर काम करता है के रूप में दर्शाया जाता है। टोर को इसके पहले तर्क के प्रक्षेप्य रिज़ॉल्यूशन का उपयोग करके परिभाषित किया गया है। हालाँकि, यह पता चला है $\operatorname {Tor} _{i}(M,N)=\operatorname {Tor} _{i}(N,M)$. हालाँकि इसे वर्णक्रमीय अनुक्रम के बिना सत्यापित किया जा सकता है, वर्णक्रमीय अनुक्रम के साथ यह बहुत आसान है।

प्रक्षेप्य संकल्प चुनें $P_{\bullet }$ और $Q_{\bullet }$ क्रमशः एम और एन का। इन्हें ऐसे कॉम्प्लेक्स के रूप में मानें जो क्रमशः डी और ई के अंतर के साथ नकारात्मक डिग्री में गायब हो जाते हैं। हम एक दोहरा कॉम्प्लेक्स बना सकते हैं जिसकी शर्तें हैं $C_{i,j}=P_{i}\otimes Q_{j}$ और किसके अंतर हैं $d\otimes 1$ और $(-1)^{i}(1\otimes e)$. (-1 का कारक यह है कि अंतर एंटीकम्यूट होते हैं।) चूंकि प्रक्षेप्य मॉड्यूल सपाट होते हैं, एक प्रक्षेप्य मॉड्यूल के साथ टेंसर उत्पाद को लेना होमोलॉजी लेने के साथ कम्यूट होता है, इसलिए हमें मिलता है:

$H_{p}^{I}(H_{q}^{II}(P_{\bullet }\otimes Q_{\bullet }))=H_{p}^{I}(P_{\bullet }\otimes H_{q}^{II}(Q_{\bullet }))$

$H_{q}^{II}(H_{p}^{I}(P_{\bullet }\otimes Q_{\bullet }))=H_{q}^{II}(H_{p}^{I}(P_{\bullet })\otimes Q_{\bullet })$

चूँकि दोनों कॉम्प्लेक्स रिज़ॉल्यूशन हैं, उनकी समरूपता डिग्री शून्य के बाहर गायब हो जाती है। डिग्री शून्य में, हम बचे हैं

$H_{p}^{I}(P_{\bullet }\otimes N)=\operatorname {Tor} _{p}(M,N)$

$H_{q}^{II}(M\otimes Q_{\bullet })=\operatorname {Tor} _{q}(N,M)$

विशेष रूप से, $E_{p,q}^{2}$ पंक्ति q = 0 (I वर्णक्रमीय अनुक्रम के लिए) और p = 0 (II वर्णक्रमीय अनुक्रम के लिए) को छोड़कर शब्द गायब हो जाते हैं। इसका तात्पर्य यह है कि वर्णक्रमीय अनुक्रम दूसरी शीट पर ख़राब हो जाता है, इसलिए ई^∞शब्द E के समरूपी हैं²शर्तें:

$\operatorname {Tor} _{p}(M,N)\cong E_{p}^{\infty }=H_{p}(T(C_{\bullet ,\bullet }))$

$\operatorname {Tor} _{q}(N,M)\cong E_{q}^{\infty }=H_{q}(T(C_{\bullet ,\bullet }))$

अंत में, जब p और q बराबर होते हैं, तो दाएँ हाथ की दोनों भुजाएँ बराबर होती हैं, और Tor की क्रमविनिमेयता अनुसरण करती है।

कार्यान्वित उदाहरण

प्रथम-चतुर्थांश शीट

एक वर्णक्रमीय अनुक्रम पर विचार करें जहां $E_{r}^{p,q}$ सभी के लिए गायब हो जाता है $p$ कुछ से कम $p_{0}$ और सभी के लिए $q$ कुछ से कम $q_{0}$. अगर $p_{0}$ और $q_{0}$ शून्य होने के लिए चुना जा सकता है, इसे प्रथम-चतुर्थांश वर्णक्रमीय अनुक्रम कहा जाता है। अनुक्रम समाप्त हो गया क्योंकि $E_{r+i}^{p,q}=E_{r}^{p,q}$ सभी के लिए धारण करता है $i\geq 0$ अगर $r>p$ और $r>q+1$. इसे देखने के लिए, ध्यान दें कि विचार किए गए मामलों के लिए या तो डोमेन या अंतर का कोडोमेन शून्य है। दृश्य संदर्भ में, चादरें एक बढ़ते हुए आयत में स्थिर हो जाती हैं (ऊपर चित्र देखें)। हालाँकि, वर्णक्रमीय अनुक्रम को ख़राब होने की आवश्यकता नहीं है, क्योंकि सभी विभेदक मानचित्र एक ही बार में शून्य नहीं हो सकते हैं। इसी प्रकार, वर्णक्रमीय अनुक्रम भी अभिसरित होता है यदि $E_{r}^{p,q}$ सभी के लिए गायब हो जाता है $p$ कुछ से अधिक $p_{0}$ और सभी के लिए $q$ कुछ से अधिक $q_{0}$.

2 गैर-शून्य आसन्न कॉलम

होने देना $E_{p,q}^{r}$ ऐसा एक समरूप वर्णक्रमीय अनुक्रम बनें $E_{p,q}^{2}=0$ 0, 1 के अलावा सभी पी के लिए। दृश्यमान रूप से, यह वर्णक्रमीय अनुक्रम है $E^{2}$-पृष्ठ

${\begin{matrix}&\vdots &\vdots &\vdots &\vdots &\\\cdots &0&E_{0,2}^{2}&E_{1,2}^{2}&0&\cdots \\\cdots &0&E_{0,1}^{2}&E_{1,1}^{2}&0&\cdots \\\cdots &0&E_{0,0}^{2}&E_{1,0}^{2}&0&\cdots \\\cdots &0&E_{0,-1}^{2}&E_{1,-1}^{2}&0&\cdots \\&\vdots &\vdots &\vdots &\vdots &\end{matrix}}$

दूसरे पृष्ठ पर अंतरों की डिग्री (-2, 1) है, इसलिए वे फॉर्म के हैं

$d_{p,q}^{2}:E_{p,q}^{2}\to E_{p-2,q+1}^{2}$

ये सभी मानचित्र शून्य हैं

$d_{0,q}^{2}:E_{0,q}^{2}\to 0$, $d_{1,q}^{2}:E_{1,q}^{2}\to 0$

इसलिए वर्णक्रमीय अनुक्रम ख़राब हो जाता है: $E^{\infty }=E^{2}$. कहो, यह अभिसरण करता है $H_{*}$ एक निस्पंदन के साथ

$0=F_{-1}H_{n}\subset F_{0}H_{n}\subset \dots \subset F_{n}H_{n}=H_{n}$

ऐसा है कि $E_{p,q}^{\infty }=F_{p}H_{p+q}/F_{p-1}H_{p+q}$. तब $F_{0}H_{n}=E_{0,n}^{2}$, $F_{1}H_{n}/F_{0}H_{n}=E_{1,n-1}^{2}$, $F_{2}H_{n}/F_{1}H_{n}=0$, $F_{3}H_{n}/F_{2}H_{n}=0$, आदि। इस प्रकार, सटीक क्रम है:

$0\to E_{0,n}^{2}\to H_{n}\to E_{1,n-1}^{2}\to 0$.

अगला, चलो $E_{p,q}^{r}$ एक वर्णक्रमीय अनुक्रम हो जिसके दूसरे पृष्ठ में केवल दो पंक्तियाँ q = 0, 1 हों। इसे दूसरे पृष्ठ पर ख़राब होने की आवश्यकता नहीं है लेकिन यह अभी भी तीसरे पृष्ठ पर ख़राब हो जाता है क्योंकि वहाँ के अंतरों की डिग्री (-3, 2) है। टिप्पणी $E_{p,0}^{3}=\operatorname {ker} (d:E_{p,0}^{2}\to E_{p-2,1}^{2})$, क्योंकि हर शून्य है। इसी प्रकार, $E_{p,1}^{3}=\operatorname {coker} (d:E_{p+2,0}^{2}\to E_{p,1}^{2})$. इस प्रकार,

$0\to E_{p,0}^{\infty }\to E_{p,0}^{2}{\overset {d}{\to }}E_{p-2,1}^{2}\to E_{p-2,1}^{\infty }\to 0$.

अब, मान लीजिए, वर्णक्रमीय अनुक्रम पिछले उदाहरण की तरह निस्पंदन एफ के साथ एच में परिवर्तित हो जाता है। तब से $F_{p-2}H_{p}/F_{p-3}H_{p}=E_{p-2,2}^{\infty }=0$, $F_{p-3}H_{p}/F_{p-4}H_{p}=0$, आदि, हमारे पास है: $0\to E_{p-1,1}^{\infty }\to H_{p}\to E_{p,0}^{\infty }\to 0$. सब कुछ एक साथ रखने पर, व्यक्ति को यह मिलता है:

$\cdots \to H_{p+1}\to E_{p+1,0}^{2}{\overset {d}{\to }}E_{p-1,1}^{2}\to H_{p}\to E_{p,0}^{2}{\overset {d}{\to }}E_{p-2,1}^{2}\to H_{p-1}\to \dots .$

वांग अनुक्रम

पिछले अनुभाग में गणना को सरल तरीके से सामान्यीकृत किया गया है। एक गोले पर कंपन पर विचार करें:

$F{\overset {i}{\to }}E{\overset {p}{\to }}S^{n}$

n के साथ कम से कम 2. सेरे वर्णक्रमीय अनुक्रम है:

$E_{p,q}^{2}=H_{p}(S^{n};H_{q}(F))\Rightarrow H_{p+q}(E)$;

यानी, $E_{p,q}^{\infty }=F_{p}H_{p+q}(E)/F_{p-1}H_{p+q}(E)$ कुछ निस्पंदन के साथ $F_{\bullet }$.

तब से $H_{p}(S^{n})$ हम देखते हैं कि केवल तभी शून्येतर होता है जब p शून्य या n होता है और उस स्थिति में 'Z' के बराबर होता है $E_{p,q}^{2}$ इसमें केवल दो पंक्तियाँ हैं $p=0,n$, इसलिए $E^{2}$-पेज द्वारा दिया गया है

${\begin{matrix}&\vdots &\vdots &\vdots &&\vdots &\vdots &\vdots &\\\cdots &0&E_{0,2}^{2}&0&\cdots &0&E_{n,2}^{2}&0&\cdots \\\cdots &0&E_{0,1}^{2}&0&\cdots &0&E_{n,1}^{2}&0&\cdots \\\cdots &0&E_{0,0}^{2}&0&\cdots &0&E_{n,0}^{2}&0&\cdots \\\end{matrix}}$

इसके अलावा, तब से

$E_{p,q}^{2}=H_{p}(S^{n};H_{q}(F))=H_{q}(F)$

के लिए $p=0,n$ सार्वत्रिक गुणांक प्रमेय द्वारा, $E^{2}$ पेज जैसा दिखता है

${\begin{matrix}&\vdots &\vdots &\vdots &&\vdots &\vdots &\vdots &\\\cdots &0&H_{2}(F)&0&\cdots &0&H_{2}(F)&0&\cdots \\\cdots &0&H_{1}(F)&0&\cdots &0&H_{1}(F)&0&\cdots \\\cdots &0&H_{0}(F)&0&\cdots &0&H_{0}(F)&0&\cdots \\\end{matrix}}$

चूँकि केवल गैर-शून्य अंतर ही पर हैं $E^{n}$-पेज, द्वारा दिया गया

$d_{n,q}^{n}:E_{n,q}^{n}\to E_{0,q+n-1}^{n}$

जो है

$d_{n,q}^{n}:H_{q}(F)\to H_{q+n-1}(F)$

वर्णक्रमीय अनुक्रम परिवर्तित होता है $E^{n+1}=E^{\infty }$. गणना करके $E^{n+1}$ हमें एक सटीक क्रम मिलता है

$0\to E_{n,q-n}^{\infty }\to E_{n,q-n}^{n}{\overset {d}{\to }}E_{0,q-1}^{n}\to E_{0,q-1}^{\infty }\to 0.$

और होमोलॉजी समूहों का उपयोग करके लिखा गया है, यह है

$0\to E_{n,q-n}^{\infty }\to H_{q-n}(F){\overset {d}{\to }}H_{q-1}(F)\to E_{0,q-1}^{\infty }\to 0.$

यह स्थापित करने के लिए कि दोनों क्या हैं $E^{\infty }$-शर्तें हैं, लिखो $H=H(E)$, और तबसे $F_{1}H_{q}/F_{0}H_{q}=E_{1,q-1}^{\infty }=0$, आदि, हमारे पास है: $E_{n,q-n}^{\infty }=F_{n}H_{q}/F_{0}H_{q}$ और इस प्रकार, तब से $F_{n}H_{q}=H_{q}$,

$0\to E_{0,q}^{\infty }\to H_{q}\to E_{n,q-n}^{\infty }\to 0.$

यह सटीक क्रम है

$0\to H_{q}(F)\to H_{q}(E)\to H_{q-n}(F)\to 0.$

सभी गणनाओं को एक साथ रखने पर, यह प्राप्त होता है:

$\dots \to H_{q}(F){\overset {i_{*}}{\to }}H_{q}(E)\to H_{q-n}(F){\overset {d}{\to }}H_{q-1}(F){\overset {i_{*}}{\to }}H_{q-1}(E)\to H_{q-n-1}(F)\to \dots$

(गाइसिन अनुक्रम एक समान तरीके से प्राप्त किया जाता है।)

निम्न-डिग्री पद

एक स्पष्ट सांकेतिक परिवर्तन के साथ, पिछले उदाहरणों में गणना के प्रकार को कोहोमोलॉजिकल वर्णक्रमीय अनुक्रम के लिए भी किया जा सकता है। होने देना $E_{r}^{p,q}$ घटते निस्पंदन के साथ एच में परिवर्तित होने वाला प्रथम-चतुर्थांश वर्णक्रमीय अनुक्रम बनें

$0=F^{n+1}H^{n}\subset F^{n}H^{n}\subset \dots \subset F^{0}H^{n}=H^{n}$

ताकि $E_{\infty }^{p,q}=F^{p}H^{p+q}/F^{p+1}H^{p+q}.$ तब से $E_{2}^{p,q}$ यदि p या q ऋणात्मक है तो शून्य है, हमारे पास है:

$0\to E_{\infty }^{0,1}\to E_{2}^{0,1}{\overset {d}{\to }}E_{2}^{2,0}\to E_{\infty }^{2,0}\to 0.$

तब से $E_{\infty }^{1,0}=E_{2}^{1,0}$ उसी कारण से और तब से $F^{2}H^{1}=0,$

$0\to E_{2}^{1,0}\to H^{1}\to E_{\infty }^{0,1}\to 0$.

तब से $F^{3}H^{2}=0$, $E_{\infty }^{2,0}\subset H^{2}$. अनुक्रमों को एक साथ रखने पर, हमें तथाकथित पाँच-अवधि का सटीक अनुक्रम मिलता है:

$0\to E_{2}^{1,0}\to H^{1}\to E_{2}^{0,1}{\overset {d}{\to }}E_{2}^{2,0}\to H^{2}.$

किनारे के नक्शे और अतिक्रमण

समजात वर्णक्रमीय अनुक्रम

होने देना $E_{p,q}^{r}$ एक वर्णक्रमीय अनुक्रम हो. अगर $E_{p,q}^{r}=0$ प्रत्येक q < 0 के लिए, तो यह होना चाहिए: r ≥ 2 के लिए,

$E_{p,0}^{r+1}=\operatorname {ker} (d:E_{p,0}^{r}\to E_{p-r,r-1}^{r})$

चूँकि हर शून्य है। इसलिए, मोनोमोर्फिज्म का एक क्रम है:

$E_{p,0}^{r}\to E_{p,0}^{r-1}\to \dots \to E_{p,0}^{3}\to E_{p,0}^{2}$.

इन्हें किनारे के मानचित्र कहा जाता है। इसी प्रकार, यदि $E_{p,q}^{r}=0$ प्रत्येक पी <0 के लिए, फिर एपिमोर्फिज्म का एक क्रम होता है (जिसे किनारे के नक्शे भी कहा जाता है):

$E_{0,q}^{2}\to E_{0,q}^{3}\to \dots \to E_{0,q}^{r-1}\to E_{0,q}^{r}$.

अतिक्रमण मानचित्र आंशिक रूप से परिभाषित मानचित्र है (अधिक सटीक रूप से, एक योगात्मक संबंध)

$\tau :E_{p,0}^{2}\to E_{0,p-1}^{2}$

एक रचना के रूप में दिया गया है $E_{p,0}^{2}\to E_{p,0}^{p}{\overset {d}{\to }}E_{0,p-1}^{p}\to E_{0,p-1}^{2}$, पहला और आखिरी मानचित्र किनारे के मानचित्रों के व्युत्क्रम हैं।

कोहोमोलॉजिकल वर्णक्रमीय अनुक्रम

वर्णक्रमीय अनुक्रम के लिए $E_{r}^{p,q}$ कोहोमोलॉजिकल प्रकार के, अनुरूप कथन धारण करते हैं। अगर $E_{r}^{p,q}=0$ प्रत्येक q < 0 के लिए, फिर एपिमोर्फिज्म का एक क्रम होता है

$E_{2}^{p,0}\to E_{3}^{p,0}\to \dots \to E_{r-1}^{p,0}\to E_{r}^{p,0}$.

और अगर $E_{r}^{p,q}=0$ प्रत्येक p < 0 के लिए, एकरूपता का एक क्रम होता है:

$E_{r}^{0,q}\to E_{r-1}^{0,q}\to \dots \to E_{3}^{0,q}\to E_{2}^{0,q}$.

यह आवश्यक नहीं है कि अपराध एक अच्छी तरह से परिभाषित मानचित्र हो:

$\tau :E_{2}^{0,q-1}\to E_{2}^{q,0}$

प्रेरक $d:E_{q}^{0,q-1}\to E_{q}^{q,0}$.

आवेदन

सेरे वर्णक्रमीय अनुक्रम में कई अंतरों की गणना के लिए इन मानचित्रों का निर्धारण मौलिक है। उदाहरण के लिए, अतिक्रमण मानचित्र अंतर निर्धारित करता है

$d_{n}:E_{n,0}^{n}\to E_{0,n-1}^{n}$

समजात वर्णक्रमीय वर्णक्रमीय अनुक्रम के लिए, इसलिए कंपन के लिए सेरे वर्णक्रमीय अनुक्रम पर $F\to E\to B$ नक्शा देता है

$d_{n}:H_{n}(B)\to H_{n-1}(F)$.

आगे के उदाहरण

कुछ उल्लेखनीय वर्णक्रमीय अनुक्रम हैं:

टोपोलॉजी और ज्यामिति

• अतियाह-हिर्ज़ेब्रुच एक असाधारण कोहोमोलॉजी सिद्धांत का वर्णक्रमीय अनुक्रम
• किसी समूह के वर्गीकृत स्थान की समरूपता के लिए बार वर्णक्रमीय अनुक्रम।
• बॉकस्टीन वर्णक्रमीय अनुक्रम मॉड पी गुणांक और होमोलॉजी कम मॉड पी के साथ होमोलॉजी से संबंधित है।
• कार्टन-लेरे वर्णक्रमीय अनुक्रम भागफल स्थान की समरूपता में परिवर्तित होता है।
• फाइब्रेशन के ठहराना की एकवचन सहसंरचना के लिए ईलेनबर्ग-मूर वर्णक्रमीय अनुक्रम
• एक कंपन का क्रमिक वर्णक्रमीय अनुक्रम

समरूपता सिद्धांत

• स्थिर समरूपता सिद्धांत में एडम्स वर्णक्रमीय अनुक्रम
• एडम्स-नोविकोव वर्णक्रमीय अनुक्रम, असाधारण कोहोमोलॉजी सिद्धांत का एक सामान्यीकरण।
• बैरेट वर्णक्रमीय अनुक्रम एक सह-फाइब्रेशन के प्रारंभिक स्थान की समरूपता में परिवर्तित होता है।
• बूसफ़ील्ड-कान वर्णक्रमीय अनुक्रम एक फ़ैक्टर के होमोटोपी कोलिमिट में परिवर्तित होता है।
• एडम्स-नोविकोव वर्णक्रमीय अनुक्रम के प्रारंभिक शब्दों की गणना के लिए रंगीन वर्णक्रमीय अनुक्रम।
• कोबार वर्णक्रमीय अनुक्रम
• ईएचपी वर्णक्रमीय अनुक्रम गोले के स्थिर समरूप समूहों में परिवर्तित होता है
• फ़ंक्शन स्पेस के होमोटॉपी समूहों में परिवर्तित होने वाला फ़ेडरर वर्णक्रमीय अनुक्रम।
• होमोटोपी निश्चित बिंदु वर्णक्रमीय अनुक्रम
• किसी स्थान की समरूपता से उसकी समरूपता की गणना के लिए ह्यूरविक्ज़ वर्णक्रमीय अनुक्रम।
• मिलर वर्णक्रमीय अनुक्रम किसी स्थान के मॉड पी स्थिर समरूपता में परिवर्तित होता है।
• मिल्नोर वर्णक्रमीय अनुक्रम बार वर्णक्रमीय अनुक्रम का दूसरा नाम है।
• मूर वर्णक्रमीय अनुक्रम बार वर्णक्रमीय अनुक्रम का दूसरा नाम है।
• एक सरल समूह की समरूपता की गणना के लिए क्विलेन वर्णक्रमीय अनुक्रम।
• रोथेनबर्ग-स्टीनरोड वर्णक्रमीय अनुक्रम बार वर्णक्रमीय अनुक्रम का दूसरा नाम है।
• रिक्त स्थान की एक पच्चर की समरूपता की गणना के लिए वैन कम्पेन वर्णक्रमीय अनुक्रम।

बीजगणित

• सेच कोहोमोलॉजी से शीफ कोहोमोलॉजी तक सेच-से-व्युत्पन्न फ़ंक्टर वर्णक्रमीय अनुक्रम।
• मॉड्यूल के टोर और एक्सट समूहों की गणना के लिए रिंग्स वर्णक्रमीय अनुक्रमों का परिवर्तन।
• कोन्स वर्णक्रमीय अनुक्रम बीजगणित के चक्रीय समरूपता में परिवर्तित होते हैं।
• गेर्स्टन-विट वर्णक्रमीय अनुक्रम
• कोहोमोलोजी शर्ट के लिए ग्रीन का वर्णक्रमीय अनुक्रम
• व्युत्पन्न फ़ंक्शनलर्स की रचना के लिए ग्रोथेंडिक वर्णक्रमीय अनुक्रम
• हाइपरहोमोलॉजी की गणना के लिए हाइपरहोमोलॉजी वर्णक्रमीय अनुक्रम।
• विभेदक बीजगणित के टेंसर उत्पाद की समरूपता की गणना के लिए कुनेथ वर्णक्रमीय अनुक्रम।
• लेरे वर्णक्रमीय अनुक्रम एक शीफ की सहसंरचना में परिवर्तित होता है।
• स्थानीय-से-वैश्विक विस्तार वर्णक्रमीय अनुक्रम
• लिंडन-होच्सचाइल्ड-समूह सहसंरचना में सेरे वर्णक्रमीय अनुक्रम|समूह (सह)होमोलॉजी
• बीजगणित के टोर या एक्सट समूहों की गणना के लिए वर्णक्रमीय अनुक्रम हो सकता है।
• विभेदक फ़िल्टर किए गए समूह का वर्णक्रमीय अनुक्रम: इस आलेख में वर्णित है।
• डबल कॉम्प्लेक्स का वर्णक्रमीय अनुक्रम: इस आलेख में वर्णित है।
• सटीक जोड़े का वर्णक्रमीय अनुक्रम: इस आलेख में वर्णित है।
• सार्वभौमिक गुणांक वर्णक्रमीय अनुक्रम
• वैन एस्ट वर्णक्रमीय अनुक्रम सापेक्ष लाई बीजगणित कोहोमोलॉजी में परिवर्तित हो रहा है।

जटिल और बीजगणितीय ज्यामिति

• एकवचन सिद्धांत में अर्नोल्ड का वर्णक्रमीय अनुक्रम।
• ब्लोच-लिचटेनबाम वर्णक्रमीय अनुक्रम एक क्षेत्र के बीजगणितीय K-सिद्धांत में परिवर्तित होता है।
• फ्रोलिचर वर्णक्रमीय अनुक्रम डोल्बौल्ट कोहोमोलॉजी से शुरू होता है और एक किस्म के बीजगणितीय डी राम कोहोमोलॉजी में परिवर्तित होता है।
• हॉज-डी राम वर्णक्रमीय अनुक्रम एक किस्म के बीजगणितीय डी राम कोहोमोलॉजी में परिवर्तित होता है।
• मोटिविक-टू-के-थ्योरी वर्णक्रमीय अनुक्रम|मोटिविक-टू-के-थ्योरी वर्णक्रमीय अनुक्रम

संदर्भ

परिचयात्मक

• Fomenko, Anatoly; Fuchs, Dmitry, Homotopical Topology
• Hatcher, Allen. "बीजगणितीय टोपोलॉजी में वर्णक्रमीय अनुक्रम" (PDF).

संदर्भ

• Leray, Jean (1946a), "L'anneau d'homologie d'une représentation", Les Comptes rendus de l'Académie des sciences, 222: 1366–1368
• Leray, Jean (1946b), "Structure de l'anneau d'homologie d'une représentation", Les Comptes rendus de l'Académie des sciences, 222: 1419–1422
• Koszul, Jean-Louis (1947). "Sur les opérateurs de dérivation dans un anneau". Comptes rendus de l'Académie des Sciences. 225: 217–219.
• Massey, William S. (1952). "Exact couples in algebraic topology. I, II". Annals of Mathematics. Second Series. Annals of Mathematics. 56 (2): 363–396. doi:10.2307/1969805. JSTOR 1969805.
• Massey, William S. (1953). "Exact couples in algebraic topology. III, IV, V". Annals of Mathematics. Second Series. Annals of Mathematics. 57 (2): 248–286. doi:10.2307/1969858. JSTOR 1969858.
• May, J. Peter. "A primer on spectral sequences" (PDF). Archived (PDF) from the original on 21 Jun 2020. Retrieved 21 Jun 2020.
• McCleary, John (2001). A User's Guide to Spectral Sequences. Cambridge Studies in Advanced Mathematics. Vol. 58 (2nd ed.). Cambridge University Press. ISBN 978-0-521-56759-6. MR 1793722.
• Mosher, Robert; Tangora, Martin (1968), Cohomology Operations and Applications in Homotopy Theory, Harper and Row, ISBN 978-0-06-044627-7
• Weibel, Charles A. (1994). An introduction to homological algebra. Cambridge Studies in Advanced Mathematics. Vol. 38. Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324. OCLC 36131259.

अग्रिम पठन

• Chow, Timothy Y. (2006). "You Could Have Invented Spectral Sequences" (PDF). Notices of the American Mathematical Society. 53: 15–19.

बाहरी संबंध

• "What is so "spectral" about spectral sequences?". MathOverflow.
• "SpectralSequences — a package for working with filtered complexes and spectral sequences". Macaulay2.