विलक्षणता (गणित)

गणित में, एक विलक्षणता एक ऐसा बिंदु है जिस पर किसी दिए गए गणितीय वस्तु को परिभाषित नहीं किया जाता है, या एक ऐसा बिंदु जहां गणितीय वस्तु किसी विशेष तरीके से अच्छी तरह से व्यवहार करना बंद कर देती है, जैसे कि व्युत्पन्न या होलोमोर्फिक कार्यों की विश्लेषणात्मकता की कमी के कारण। उदाहरण के लिए, एक वास्तविक चर का कार्य

$f(x)={\frac {1}{x}}$

में एक विलक्षणता है $x=0$, जहां फ़ंक्शन का संख्यात्मक मान निकट आता है $\pm \infty$ इसलिए फ़ंक्शन परिभाषित नहीं है। निरपेक्ष मान फ़ंक्शन $g(x)=|x|$ में एक विलक्षणता भी है $x=0$, क्योंकि यह वहां विभेदक कार्य नहीं है। द्वारा परिभाषित बीजीय वक्र $\left\{(x,y):y^{3}-x^{2}=0\right\}$ में $(x,y)$ समन्वय प्रणाली में एक विलक्षणता होती है (जिसे एक पुच्छ (विलक्षणता) कहा जाता है) पर $(0,0)$. बीजगणितीय ज्यामिति में विलक्षणताओं के लिए, बीजीय किस्म का एकवचन बिंदु देखें। विभेदक ज्यामिति में विलक्षणताओं के लिए, विलक्षणता सिद्धांत देखें।

वास्तविक विश्लेषण

वास्तविक विश्लेषण में, विलक्षणताएं या तो असंततता का वर्गीकरण हैं, या व्युत्पन्न की असंततता (कभी-कभी उच्च क्रम के डेरिवेटिव की असंततता भी)। चार प्रकार के असंतुलन हैं: प्रकार I, जिसमें दो उपप्रकार हैं, और प्रकार II, जिसे दो उपप्रकारों में भी विभाजित किया जा सकता है (हालांकि आमतौर पर नहीं)।

यह वर्णन करने के लिए कि इन दो प्रकार की सीमाओं का किस प्रकार उपयोग किया जा रहा है, मान लीजिए कि $f(x)$ एक वास्तविक तर्क का एक कार्य है $x$, और इसके तर्क के किसी भी मूल्य के लिए, कहें $c$, फिर बाएं हाथ की सीमा, $f(c^{-})$, और दाहिने हाथ की सीमा, $f(c^{+})$, द्वारा परिभाषित किया गया है:

$f(c^{-})=\lim _{x\to c}f(x)$, सीमित $x<c$ तथा

$f(c^{+})=\lim _{x\to c}f(x)$, सीमित $x>c$.

मूल्य $f(c^{-})$ वह मान है जो फ़ंक्शन $f(x)$ मूल्य के रूप में जाता है $x$ दृष्टिकोण $c$ नीचे से, और मूल्य $f(c^{+})$ वह मान है जो फ़ंक्शन $f(x)$ मूल्य के रूप में जाता है $x$ दृष्टिकोण $c$ ऊपर से, वास्तविक मान की परवाह किए बिना फ़ंक्शन का उस बिंदु पर है जहां $x=c$.

कुछ ऐसे कार्य हैं जिनके लिए ये सीमाएँ बिल्कुल भी मौजूद नहीं हैं। उदाहरण के लिए, फ़ंक्शन

$g(x)=\sin \left({\frac {1}{x}}\right)$

किसी भी चीज़ की ओर प्रवृत्त नहीं होता $x$ दृष्टिकोण $c=0$. इस मामले में सीमाएं अनंत नहीं हैं, बल्कि अपरिभाषित (गणित) हैं: इसका कोई मूल्य नहीं है $g(x)$ पर बस जाता है। जटिल विश्लेषण से उधार लेते हुए, इसे कभी-कभी एक आवश्यक विलक्षणता कहा जाता है।

किसी दिए गए मान पर संभावित मामले $c$ तर्क के लिए इस प्रकार हैं।

• निरंतरता का एक बिंदु का मान है $c$ जिसके लिए $f(c^{-})=f(c)=f(c^{+})$, जैसा कि एक सुचारू कार्य की अपेक्षा करता है। सभी मान सीमित होने चाहिए। यदि $c$ निरंतरता का बिंदु नहीं है, तो एक असंतुलन होता है $c$.
• एक प्रकार I असंतुलन तब होता है जब दोनों $f(c^{-})$ तथा $f(c^{+})$ मौजूद हैं और परिमित हैं, लेकिन निम्न तीन शर्तों में से कम से कम एक भी लागू होता है:
  • $f(c^{-})\neq f(c^{+})$;
  • $f(x)$ के मामले के लिए परिभाषित नहीं है $x=c$; या
  • $f(c)$ एक परिभाषित मूल्य है, जो, हालांकि, दो सीमाओं के मूल्य से मेल नहीं खाता है।

  टाइप I डिसकंटीनिटीज को निम्नलिखित उपप्रकारों में से एक के रूप में और अधिक प्रतिष्ठित किया जा सकता है:

  • एक छलांग विच्छेद तब होता है जब $f(c^{-})\neq f(c^{+})$, की परवाह किए बिना कि क्या $f(c)$ परिभाषित किया गया है, और इसके मूल्य की परवाह किए बिना यदि इसे परिभाषित किया गया है।
  • एक हटाने योग्य विलक्षणता तब होती है जब $f(c^{-})=f(c^{+})$, इस बात की परवाह किए बिना कि $f(c)$ परिभाषित किया गया है, और इसके मूल्य की परवाह किए बिना यदि इसे परिभाषित किया गया है (लेकिन जो दो सीमाओं से मेल नहीं खाता है)।
• टाइप II डिसकंटीनिटी तब होती है जब या तो $f(c^{-})$ या $f(c^{+})$ मौजूद नहीं है (संभवतः दोनों)। इसके दो उपप्रकार हैं, जिन्हें आमतौर पर अलग से नहीं माना जाता है:
  • एक अनंत असंततता विशेष मामला है जब या तो बाएं हाथ या दाहिने हाथ की सीमा मौजूद नहीं है, विशेष रूप से क्योंकि यह अनंत है, और दूसरी सीमा भी अनंत है, या कुछ अच्छी तरह से परिभाषित परिमित संख्या है। दूसरे शब्दों में, जब किसी फ़ंक्शन के ग्राफ़ में एक लंबवत अनंतस्पर्शी होता है, तो फ़ंक्शन में अनंत असंतुलन होता है।
  • एक आवश्यक विलक्षणता जटिल विश्लेषण से उधार लिया गया शब्द है (नीचे देखें)। यह मामला है जब या तो एक या दूसरी सीमा $f(c^{-})$ या $f(c^{+})$ मौजूद नहीं है, लेकिन इसलिए नहीं कि यह एक अनंत असंततता है। आवश्यक विलक्षणताओं की कोई सीमा नहीं है, भले ही मान्य उत्तरों को शामिल करने के लिए विस्तारित किया गया हो $\pm \infty$.

वास्तविक विश्लेषण में, एक विलक्षणता या असंततता अकेले एक फ़ंक्शन की संपत्ति है। किसी फ़ंक्शन के व्युत्पन्न में मौजूद कोई भी विलक्षणता को व्युत्पन्न से संबंधित माना जाता है, न कि मूल फ़ंक्शन से।

एकवचन समन्वय

Main article: Coordinate singularity

एक समन्वय विलक्षणता तब होती है जब एक समन्वय फ्रेम में एक स्पष्ट विलक्षणता या असंतुलन होता है, जिसे एक अलग फ्रेम चुनकर हटाया जा सकता है। इसका एक उदाहरण गोलाकार निर्देशांक में 90 डिग्री अक्षांश पर स्पष्ट विलक्षणता है। एक गोले की सतह पर उत्तर की ओर बढ़ने वाली वस्तु (उदाहरण के लिए, रेखा 0 डिग्री देशांतर के साथ) अचानक ध्रुव पर देशांतर में एक तात्कालिक परिवर्तन का अनुभव करेगी (उदाहरण के मामले में, देशांतर 0 से देशांतर 180 डिग्री तक कूदना) . हालाँकि, यह असंतुलन केवल स्पष्ट है; यह चुनी गई समन्वय प्रणाली की एक कलाकृति है, जो ध्रुवों पर एकवचन है। एक अलग समन्वय प्रणाली स्पष्ट असंतोष को समाप्त कर देगी (उदाहरण के लिए, अक्षांश/देशांतर प्रतिनिधित्व को एन-वेक्टर के साथ बदलकर।n-वेक्टर प्रतिनिधित्व)।

जटिल विश्लेषण

जटिल विश्लेषण में, विलक्षणताओं के कई वर्ग हैं। इनमें पृथक विलक्षणताएं, गैर-पृथक विलक्षणताएं और शाखा बिंदु शामिल हैं।

पृथक विलक्षणता

मान लो कि $f$ एक फ़ंक्शन है जो एक बिंदु के सेट पूरक में होलोमोर्फिक फ़ंक्शन है $a$ खुले सेट में $U$ जटिल संख्या ओं का $\mathbb {C} .$ फिर:

• बिंदु $a$ की एक हटाने योग्य विलक्षणता है $f$ यदि कोई होलोमोर्फिक फ़ंक्शन मौजूद है $g$ सभी पर परिभाषित $U$ ऐसा है कि $f(z)=g(z)$ सभी के लिए $z$ में $U\setminus \{a\}$. कार्यक्रम $g$ फ़ंक्शन के लिए एक निरंतर प्रतिस्थापन है $f$.
• बिंदु $a$ एक ध्रुव (जटिल विश्लेषण) या गैर-आवश्यक विलक्षणता है $f$ यदि कोई होलोमोर्फिक फ़ंक्शन मौजूद है $g$ पर परिभाषित $U$ साथ $g(a)$ गैर-शून्य, और एक प्राकृतिक संख्या $n$ ऐसा है कि $f(z)=g(z)/(z-a)^{n}$ सभी के लिए $z$ में $U\setminus \{a\}$. कम से कम ऐसी संख्या $n$ ध्रुव का क्रम कहलाता है। गैर-आवश्यक विलक्षणता के व्युत्पन्न में स्वयं एक गैर-आवश्यक विलक्षणता होती है, जिसमें $n$ 1 की वृद्धि हुई (यदि को छोड़कर) $n$ 0 है ताकि विलक्षणता हटाने योग्य हो)।
• बिंदु $a$ की एक अनिवार्य विलक्षणता है $f$ यदि यह न तो हटाने योग्य विलक्षणता है और न ही ध्रुव। बिंदु $a$ एक आवश्यक विलक्षणता है यदि लॉरेंट श्रृंखला में नकारात्मक डिग्री की असीम रूप से कई शक्तियां हैं।

असंगत विलक्षणताएं

पृथक विलक्षणताओं के अलावा, एक चर के जटिल कार्य अन्य विलक्षण व्यवहार प्रदर्शित कर सकते हैं। इन्हें गैर-पृथक विलक्षणता कहा जाता है, जिनमें से दो प्रकार हैं:

• क्लस्टर अंक: पृथक विलक्षणताओं के अंक सीमित करें। यदि वे सभी ध्रुव हैं, उनमें से प्रत्येक पर लॉरेंट श्रृंखला के विस्तार को स्वीकार करने के बावजूद, इसकी सीमा पर ऐसा कोई विस्तार संभव नहीं है।
• प्राकृतिक सीमाएं: कोई भी गैर-पृथक सेट (उदाहरण के लिए एक वक्र) जिस पर कार्य विश्लेषणात्मक निरंतरता नहीं हो सकते हैं (या उनके बाहर यदि वे रीमैन क्षेत्र में बंद वक्र हैं)।

शाखा अंक

शाखा बिंदु आम तौर पर एक बहु-मूल्यवान फ़ंक्शन का परिणाम होते हैं, जैसे कि ${\sqrt {z}}$ या $\log(z)$, जिन्हें एक निश्चित सीमित डोमेन के भीतर परिभाषित किया जाता है ताकि फ़ंक्शन को डोमेन के भीतर एकल-मूल्यवान बनाया जा सके। कट एक लाइन या कर्व है जिसे फंक्शन के असंतत मूल्यों के बीच तकनीकी अलगाव को पेश करने के लिए डोमेन से बाहर रखा गया है। जब कट की वास्तव में आवश्यकता होती है, तो शाखा कट के प्रत्येक पक्ष पर फ़ंक्शन के अलग-अलग मान होंगे। शाखा कट का आकार पसंद का मामला है, भले ही इसे दो अलग-अलग शाखा बिंदुओं को जोड़ना चाहिए (जैसे $z=0$ तथा $z=\infty$ के लिये $\log(z)$) जो जगह में तय हो गए हैं।

परिमित समय विलक्षणता

पारस्परिक कार्य , अतिपरवलयिक वृद्धि को प्रदर्शित करता है।

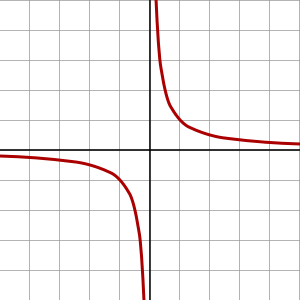
एक परिमित-समय विलक्षणता तब होती है जब एक इनपुट चर समय होता है, और एक आउटपुट चर एक सीमित समय में अनंत की ओर बढ़ता है। ये कीनेमेटीक्स का और आंशिक विभेदक समीकरण में महत्वपूर्ण हैं - अनंत शारीरिक रूप से नहीं होते हैं, लेकिन विलक्षणता के पास का व्यवहार अक्सर रुचि का होता है। गणितीय रूप से, सबसे सरल परिमित-समय की विलक्षणताएं फॉर्म के विभिन्न प्रतिपादकों के लिए शक्ति कानून हैं $x^{-\alpha },$ जिनमें से सबसे सरल अतिपरवलयिक वृद्धि है, जहां घातांक (ऋणात्मक) 1 है: $x^{-1}.$ अधिक सटीक रूप से, समय बढ़ने के साथ सकारात्मक समय पर एक विलक्षणता प्राप्त करने के लिए (इसलिए आउटपुट अनंत तक बढ़ता है), एक इसके बजाय उपयोग करता है $(t_{0}-t)^{-\alpha }$ (समय के लिए t का उपयोग करते हुए, दिशा को उलटते हुए $-t$ ताकि समय अनंत तक बढ़े, और विलक्षणता को 0 से एक निश्चित समय तक आगे ले जाए $t_{0}$)

एक विमान पर एक बेलोचदार गेंद की उछलती गति इसका एक उदाहरण होगा। यदि आदर्श गति पर विचार किया जाता है, जिसमें प्रत्येक उछाल पर गतिज ऊर्जा का समान अंश खो जाता है, तो उछाल की आवृत्ति अनंत हो जाती है, क्योंकि गेंद एक सीमित समय में आराम करती है। परिमित-समय की विलक्षणताओं के अन्य उदाहरणों में पेनलेव विरोधाभास के विभिन्न रूप शामिल हैं (उदाहरण के लिए, एक ब्लैकबोर्ड पर खींचे जाने पर चाक को छोड़ने की प्रवृत्ति), और एक सपाट सतह पर घूमने वाले सिक्के की पूर्वता दर अनंत की ओर कैसे बढ़ती है- अचानक रुकने से पहले (जैसा कि यूलर डिस्क टॉय का उपयोग करके अध्ययन किया गया है)।

काल्पनिक उदाहरणों में हेन्ज़ वॉन फ़ॉस्टर का मुखर हेनज़ वॉन फ़ॉस्टर # डूम्सडे समीकरण | डूम्सडे का समीकरण (सरलीकृत मॉडल सीमित समय में अनंत मानव आबादी उत्पन्न करते हैं) शामिल हैं।

बीजगणितीय ज्यामिति और क्रमविनिमेय बीजगणित

बीजगणितीय ज्यामिति में, बीजीय किस्म का एक विलक्षण बिंदु उस किस्म का बिंदु होता है जहां स्पर्शरेखा स्थान को नियमित रूप से परिभाषित नहीं किया जा सकता है। विलक्षणताओं का सबसे सरल उदाहरण वक्र हैं जो स्वयं को पार करते हैं। लेकिन अन्य प्रकार की विलक्षणताएं हैं, जैसे पुच्छ (विलक्षणता)। उदाहरण के लिए, समीकरण y² − x³ = 0 एक वक्र को परिभाषित करता है जिसके मूल में एक पुच्छ होता है x = y = 0. कोई परिभाषित कर सकता है x-अक्ष इस बिंदु पर एक स्पर्शरेखा के रूप में है, लेकिन यह परिभाषा अन्य बिंदुओं पर परिभाषा के समान नहीं हो सकती है। दरअसल, इस मामले में x-अक्ष एक दोहरी स्पर्शरेखा है।

एफाइन किस्म और प्रक्षेपी किस्म के लिए, विलक्षणता वे बिंदु हैं जहां जैकोबियन मैट्रिक्स में एक रैंक (रैखिक बीजगणित) होता है जो कि विविधता के अन्य बिंदुओं की तुलना में कम होता है।

कम्यूटेटिव बीजगणित के संदर्भ में एक समान परिभाषा दी जा सकती है, जो अमूर्त विविधता और योजना (गणित) तक फैली हुई है: एक बिंदु एकवचन है यदि अंगूठी का स्थानीयकरण नियमित स्थानीय अंगूठी नहीं है।

यह भी देखें

• आपदा सिद्धांत *
• परिभाषित और अपरिभाषित
• अध: पतन (गणित)
• शून्य से विभाजन
• हाइपरबोलिक ग्रोथ
• पैथोलॉजिकल (गणित)
• एकल समाधान
• हटाने योग्य विलक्षणता

इस पृष्ठ में अनुपलब्ध आंतरिक लिंक की सूची

• अंक शास्त्र
• यौगिक
• निरपेक्ष मूल्य
• पुच्छ (विलक्षण)
• अंतर ज्यामिति
• एक बीजीय किस्म का एकवचन बिंदु
• असंबद्धताओं का वर्गीकरण
• कूदना असंबद्धता
• ऊर्ध्वाधर एसिम्पटोट
• एक समारोह का ग्राफ
• पूरक सेट करें
• खुला सेट
• पोल (जटिल विश्लेषण)
• आईएफएफ
• सीमा बिंदु
• अतिशयोक्तिपूर्ण वृद्धि
• शक्ति नियम
• अग्रगमन
• सिक्का
• हेंज वॉन फ़ॉएस्टर
• सार किस्म
• एक अंगूठी का स्थानीयकरण
• नियमित स्थानीय रिंग
• क्रमविनिमेय बीजगणित
• affine किस्म
• एकवचन समाधान
• विकृति (गणित)