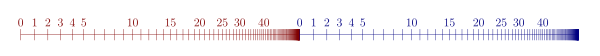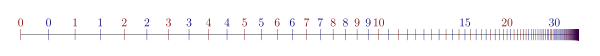सामान्य अंकगणित

सेट सिद्धांत के गणित क्षेत्र में, क्रमसूचक अंकगणित क्रमसूचक संख्याओं पर तीन सामान्य संक्रियाओं का वर्णन करता है: जोड़, गुणा और घातांक। प्रत्येक को अनिवार्य रूप से दो अलग-अलग तरीकों से परिभाषित किया जा सकता है: या तो एक स्पष्ट सुव्यवस्थित | सुव्यवस्थित सेट का निर्माण करके जो ऑपरेशन के परिणाम का प्रतिनिधित्व करता है या ट्रांसफ़िनिट रिकर्सन का उपयोग करके। कैंटर सामान्य रूप, ऑर्डिनल लिखने का एक मानकीकृत तरीका प्रदान करता है। इन सामान्य क्रमिक संक्रियाओं के अलावा, #प्राकृतिक संक्रियाएँ भी हैं| क्रमसूचकों का प्राकृतिक अंकगणित और #निंबर अंकगणित।

जोड़

दो असंयुक्त सुव्यवस्थित समुच्चयों S और T का संघ (सेट सिद्धांत) सुव्यवस्थित हो सकता है। उस संघ का ऑर्डर-प्रकार वह क्रमसूचक है जो एस और टी के ऑर्डर-प्रकारों को जोड़ने से उत्पन्न होता है। यदि दो सुव्यवस्थित सेट पहले से ही असंबद्ध नहीं हैं, तो उन्हें ऑर्डर-आइसोमोर्फिक असंयुक्त सेटों द्वारा प्रतिस्थापित किया जा सकता है, उदाहरण के लिए S को {0} × S से और T को {1} × T से बदलें। इस तरह, सुव्यवस्थित सेट S को सुव्यवस्थित सेट T के बाईं ओर लिखा जाता है, जिसका अर्थ है कि S पर एक ऑर्डर परिभाषित किया जाता है $\cup$ टी जिसमें एस का प्रत्येक तत्व टी के प्रत्येक तत्व से छोटा है। सेट (गणित) एस और टी स्वयं उस क्रम को बनाए रखते हैं जो उनके पास पहले से है।

योग α + β की परिभाषा β पर ट्रांसफिनिट रिकर्सन द्वारा भी दी जा सकती है:

• α + 0 = α
• α + S(β) = S(α + β), जहां S उत्तराधिकारी क्रमिक फ़ंक्शन को दर्शाता है।
• $\alpha +\beta =\bigcup _{\delta <\beta }(\alpha +\delta )$ जब β एक सीमा क्रमसूचक है।

प्राकृतिक संख्याओं पर क्रमिक जोड़ मानक जोड़ के समान है। पहला ट्रांसफिनिट ऑर्डिनल ω है, जो सभी प्राकृतिक संख्याओं का सेट है, इसके बाद ω + 1, ω + 2, आदि आता है। ऑर्डिनल ω + ω सामान्य तरीके से ऑर्डर की गई प्राकृतिक संख्याओं की दो प्रतियों द्वारा प्राप्त किया जाता है और दूसरी प्रतिलिपि पूरी तरह से प्राप्त की जाती है पहले के दाईं ओर. दूसरी प्रति के लिए 0' < 1' < 2' < ... लिखना, ω + ω जैसा दिखता है

0 < 1 < 2 < 3 < ... < 0' < 1' < 2' < ...

यह ω से भिन्न है क्योंकि ω में केवल 0 का कोई प्रत्यक्ष पूर्ववर्ती नहीं है जबकि ω + ω में दो तत्वों 0 और 0' का कोई प्रत्यक्ष पूर्ववर्ती नहीं है।

गुण

सामान्यतः क्रमिक जोड़ क्रमविनिमेय नहीं है। उदाहरण के लिए, 3 + ω = ω चूंकि ऑर्डर संबंध के लिए 3 + ω 0 < 1 < 2 < 0' < 1' < 2' <... है, जिसे ω में पुनः लेबल किया जा सकता है। इसके विपरीत ω + 3 ω के बराबर नहीं है क्योंकि क्रम संबंध 0 < 1 < 2 < ... < 0' < 1' < 2' में सबसे बड़ा तत्व है (अर्थात्, 2') और ω में (ω और नहीं) है ω + 3 समविभव हैं, लेकिन क्रम-समरूपी नहीं)। क्रमवाचक जोड़ अभी भी साहचर्य है; उदाहरण के लिए कोई देख सकता है कि (ω + 4) + ω = ω + (4 + ω) = ω + ω।

सही तर्क में जोड़ सख्ती से बढ़ रहा है और निरंतर है:

$\alpha <\beta \Rightarrow \gamma +\alpha <\gamma +\beta$

लेकिन वाम तर्क के लिए अनुरूप संबंध लागू नहीं होता है; इसके बजाय हमारे पास केवल:

$\alpha <\beta \Rightarrow \alpha +\gamma \leq \beta +\gamma$

क्रमिक जोड़ वाम-रद्द है: यदि α + β = α + γ, तो β = γ। इसके अलावा, कोई ऑर्डिनल्स β ≤ α के लिए बाएं विभाजन को परिभाषित कर सकता है: एक अद्वितीय γ है जैसे कि α = β + γ। दूसरी ओर, सही रद्दीकरण काम नहीं करता:

$3+\omega =0+\omega =\omega$ लेकिन $3\neq 0$

न ही सही घटाव होता है, तब भी जब β ≤ α: उदाहरण के लिए, कोई γ मौजूद नहीं है जैसे कि γ + 42 = ω।

यदि α से कम के क्रमसूचक योग के अंतर्गत बंद होते हैं और उनमें 0 होता है तो α को कभी-कभी γ-संख्या कहा जाता है (योगात्मक रूप से अविभाज्य क्रमसूचक देखें)। ये बिल्कुल ω के रूप के क्रमसूचक हैं^बी.

गुणन

असंयुक्त संघ { (0,n) : n ∈ ℕ } ∪ { (1,n) : n ∈ ℕ } में ऑर्डर प्रकार है $\omega \cdot 2$.

सेट { (n,0), (n,1) : n ∈ ℕ } में ऑर्डर प्रकार है $2\cdot \omega$, शब्दकोषीय क्रम के अंतर्गत।

दो सुव्यवस्थित सेट एस और टी के कार्टेशियन उत्पाद, एस×टी को शब्दकोषीय क्रम के एक प्रकार द्वारा अच्छी तरह से ऑर्डर किया जा सकता है जो कम से कम महत्वपूर्ण स्थिति को पहले रखता है। प्रभावी रूप से, टी के प्रत्येक तत्व को एस की एक असंयुक्त प्रतिलिपि द्वारा प्रतिस्थापित किया जाता है। कार्टेशियन उत्पाद का ऑर्डर-प्रकार वह क्रमसूचक है जो एस और टी के ऑर्डर-प्रकार को गुणा करने के परिणामस्वरूप होता है।

गुणन की परिभाषा आगमनात्मक रूप से भी दी जा सकती है (निम्नलिखित प्रेरण β पर है):

• α·0 = 0.
• α · S(β) = (α · β) + α, एक उत्तराधिकारी क्रमसूचक S(β) के लिए।
• $\alpha \cdot \beta =\bigcup _{\delta <\beta }(\alpha \cdot \delta )$, जब β एक सीमा क्रमसूचक है।

उदाहरण के तौर पर, यहां ω·2 के लिए ऑर्डर संबंध दिया गया है:

0₀ < 1₀ < 2₀ < 3₀ < ... < 0₁ < 1₁ < 2₁ < 3₁ <...,

जिसका क्रम प्रकार ω + ω के समान है। इसके विपरीत, 2·ω इस तरह दिखता है:

0₀ < 1₀ < 0₁ < 1₁ < 0₂ < 1₂ < 0₃ < 1₃ < ...

और पुनः लेबल करने के बाद, यह बिल्कुल ω जैसा दिखता है। इस प्रकार, ω·2 = ω+ω ≠ ω = 2·ω, यह दर्शाता है कि क्रमसूचकों का गुणन सामान्य रूप से क्रमविनिमेय नहीं है, c.f. चित्रों।

पुनः प्राकृतिक संख्याओं पर क्रमसूचक गुणन मानक गुणन के समान ही है।

गुण

α·0 = 0·α = 0, और शून्य-उत्पाद संपत्ति रखती है: α·β = 0 $\Rightarrow$ α = 0 या β = 0. क्रमसूचक 1 एक गुणात्मक पहचान है, α·1 = 1·α = α. गुणन साहचर्य है, (α·β)·γ = α·(β·γ)। सही तर्क में गुणन सख्ती से बढ़ रहा है और निरंतर है: (α < β और γ > 0) $\Rightarrow$ γ·α < γ·β. बाएं तर्क में गुणा सख्ती से नहीं बढ़ रहा है, उदाहरण के लिए, 1 < 2 लेकिन 1·ω = 2·ω = ω। हालाँकि, यह (सख्ती से नहीं) बढ़ रहा है, यानी α ≤ β $\Rightarrow$ α·γ ≤ β·γ.

क्रमसूचकों का गुणन सामान्यतः क्रमविनिमेय नहीं है। विशेष रूप से, 1 से बड़ी प्राकृतिक संख्या कभी भी किसी अनंत क्रमसूचक के साथ परिवर्तित नहीं होती है, और दो अनंत क्रमसूचक α, β तभी परिवर्तित होते हैं जब और केवल यदि α^म = बीⁿकुछ सकारात्मक प्राकृतिक संख्याओं m और n के लिए। संबंध α, β के साथ बदलता है, 1 से अधिक ऑर्डिनल्स पर एक तुल्यता संबंध है, और सभी तुल्यता वर्ग गणनीय रूप से अनंत हैं।

बाईं ओर वितरणता कायम है: α(β+ γ) = αβ+ αγ। हालाँकि, दाईं ओर वितरणात्मक कानून (β + γ)α = βα+γα आम तौर पर सच नहीं है: (1 + 1)·ω = 2·ω = ω जबकि 1·ω + 1·ω = ω+ω, जो फरक है। एक वाम-रद्दीकरण कानून है: यदि α > 0 और α·β = α·γ, तो β = γ। सही रद्दीकरण काम नहीं करता, उदा. 1·ω = 2·ω = ω, लेकिन 1 और 2 भिन्न हैं। शेष संपत्ति के साथ एक बायां विभाजन मानता है: सभी α और β के लिए, यदि β > 0, तो अद्वितीय γ और δ हैं जैसे कि α = β·γ + δ और δ < β। सही विभाजन काम नहीं करता: ऐसा कोई α नहीं है जो α·ω ≤ ω हो^ω ≤ (α+1)·ω.

क्रमसूचक संख्याएँ बायें निकट-सेमीरिंग बनाती हैं, लेकिन एक वलय (बीजगणित) नहीं बनाती हैं। इसलिए ऑर्डिनल्स एक यूक्लिडियन डोमेन नहीं हैं, क्योंकि वे एक रिंग भी नहीं हैं - इसके अलावा यहां बाएं डिवीजन का उपयोग करके यूक्लिडियन मानदंड को ऑर्डिनल-वैल्यू किया जाएगा।

एक δ-संख्या (देखें योगात्मक रूप से अविभाज्य क्रमसूचक#गुणात्मक रूप से अविभाज्य) एक क्रमसूचक β है जो 1 से बड़ा है जैसे कि αβ=β जब भी 0 < α < β हो। इनमें क्रमसूचक 2 और β=ω रूप के क्रमसूचक शामिल हैं^ωसी.

घातांक

ऑर्डर प्रकारों के माध्यम से परिभाषा को ऑर्डिनल नंबर#वॉन न्यूमैन की ऑर्डिनल्स की परिभाषा का उपयोग करके सबसे आसानी से समझाया गया है|वॉन न्यूमैन की सभी छोटे ऑर्डिनल्स के सेट के रूप में एक ऑर्डिनल की परिभाषा। फिर, ऑर्डर प्रकार α का एक सेट बनाने के लिए^β β से α तक सभी कार्यों पर विचार करें जैसे कि डोमेन β के तत्वों की केवल एक सीमित संख्या α के एक गैर शून्य तत्व पर मैप करती है (अनिवार्य रूप से, हम परिमित समर्थन (गणित) के साथ कार्यों पर विचार करते हैं)। आदेश सबसे कम महत्वपूर्ण स्थिति के साथ शब्दकोषीय है।

घातांक की परिभाषा आगमनात्मक रूप से भी दी जा सकती है (निम्नलिखित प्रेरण β, घातांक पर है):

• α⁰=1.
• α^S(β) = (α^β) · α, एक उत्तराधिकारी क्रमसूचक S(β) के लिए।
• $\alpha ^{\beta }=\bigcup _{0<\delta <\beta }(\alpha ^{\delta })$, जब β एक सीमा क्रमसूचक है।

परिमित घातांक के लिए क्रमसूचक घातांक की परिभाषा सीधी है। यदि घातांक एक सीमित संख्या है, तो घात पुनरावृत्त गुणन का परिणाम है। उदाहरण के लिए, ω² = ω·ω क्रमसूचक गुणन की संक्रिया का उपयोग करते हुए। ध्यान दें कि ω·ω को 2 = {0,1} से ω = {0,1,2,...} तक फ़ंक्शंस के सेट का उपयोग करके परिभाषित किया जा सकता है, पहले कम से कम महत्वपूर्ण स्थिति के साथ लेक्सिकोग्राफ़िक क्रम का आदेश दिया गया है:

(0,0) < (1,0) < (2,0) < (3,0) < ... < (0,1) < (1,1) < (2,1) < (3, 1) < ... < (0,2) < (1,2) < (2,2) < ...

यहां संक्षिप्तता के लिए, हमने फ़ंक्शन {(0,k), (1,m)} को क्रमित जोड़ी (k, m) से बदल दिया है।

इसी प्रकार, किसी भी परिमित घातांक n के लिए, $\omega ^{n}$ n (डोमेन) से प्राकृतिक संख्याओं (कोडोमेन) तक कार्यों के सेट का उपयोग करके परिभाषित किया जा सकता है। इन कार्यों को प्राकृतिक संख्याओं के टुपल|एन-ट्यूपल्स के रूप में संक्षिप्त किया जा सकता है।

लेकिन अनंत घातांकों के लिए, परिभाषा स्पष्ट नहीं हो सकती है। एक सीमा क्रमसूचक, जैसे ω^ω, सभी छोटे अध्यादेशों का सर्वोच्च है। ω को परिभाषित करना स्वाभाविक लग सकता है^ωप्राकृतिक संख्याओं के सभी अनंत अनुक्रमों के सेट का उपयोग करना। हालाँकि, हम पाते हैं कि इस सेट पर कोई भी निरपेक्षता (गणितीय तर्क) परिभाषित क्रम सुव्यवस्थित नहीं है। इस समस्या से निपटने के लिए परिभाषा सेट को उन अनुक्रमों तक सीमित करती है जो केवल सीमित संख्या में तर्कों के लिए गैर-शून्य हैं। यह स्वाभाविक रूप से आधार की सीमित शक्तियों की सीमा के रूप में प्रेरित है (बीजगणित में सहउत्पाद की अवधारणा के समान)। इसे अनंत मिलन के रूप में भी सोचा जा सकता है $\bigcup _{n<\omega }\omega ^{n}$.

उनमें से प्रत्येक अनुक्रम एक से कम क्रमसूचक से मेल खाता है $\omega ^{\omega }$ जैसे कि $\omega ^{n_{1}}c_{1}+\omega ^{n_{2}}c_{2}+\cdots +\omega ^{n_{k}}c_{k}$ और $\omega ^{\omega }$ उन सभी छोटे अध्यादेशों में सर्वोच्च है।

इस सेट पर शब्दकोषीय क्रम एक सुव्यवस्थित क्रम है जो दशमलव संकेतन में लिखी गई प्राकृतिक संख्याओं के क्रम से मिलता जुलता है, सिवाय इसके कि अंकों की स्थिति उलट जाती है, और केवल अंक 0-9 के बजाय मनमानी प्राकृतिक संख्याएँ होती हैं:

(0,0,0,...) < (1,0,0,0,...) < (2,0,0,0,...) < ... <

(0,1,0,0,0,...) < (1,1,0,0,0,...) < (2,1,0,0,0,...) < . .. <

(0,2,0,0,0,...) < (1,2,0,0,0,...) < (2,2,0,0,0,...)

< ... <

(0,0,1,0,0,0,...) < (1,0,1,0,0,0,...) < (2,0,1,0,0,0, ...)

<...

सामान्य तौर पर, किसी भी क्रमसूचक α को α प्राप्त करने के लिए उसी तरह से दूसरे क्रमसूचक β की शक्ति तक बढ़ाया जा सकता है^बी.

हम देखतें है

• 1^ω = 1,
• 2^ω = ω,
• 2^ω+1 = ω·2 = ω+ω.

जबकि समान संकेतन का उपयोग क्रमसूचक घातांक और कार्डिनल घातांक के लिए किया जाता है, क्रमसूचक घातांक कार्डिनल घातांक से काफी भिन्न होता है। उदाहरण के लिए, क्रमिक घातांक के साथ $2^{\omega }=\omega$, लेकिन के लिए $\aleph _{0}$(एलेफ़ शून्य, की प्रमुखता $\omega$), $2^{\aleph _{0}}>\aleph _{0}$. यहाँ, $2^{\aleph _{0}}$ सभी प्राकृतिक संख्याओं के समुच्चय से लेकर दो तत्वों वाले समुच्चय तक सभी कार्यों के समुच्चय की प्रमुखता है। (यह सभी प्राकृतिक संख्याओं के सेट की शक्ति सेट की कार्डिनैलिटी है और इसके बराबर है ${\mathfrak {c}}$, सातत्य की कार्डिनैलिटी।) कार्डिनल घातांक के साथ क्रमवाचक घातांक को भ्रमित करने से बचने के लिए, कोई पूर्व में क्रमवाचक (जैसे ω) के लिए प्रतीकों और कार्डिनल्स के लिए प्रतीकों (जैसे) का उपयोग कर सकता है। $\aleph _{0}$) बाद वाले में।

गुण

• α⁰=1.
• यदि 0 < α, तो 0^α = 0.
• 1^α = 1.
• ए¹=ए.
• ए^बी·ए^सी = ए^{बी + सी}.
• (ए^ख)^सी = ए^b·c.
• वहाँ α, β, और γ हैं जिसके लिए (α·β)^सी ≠ ए^सी·बी^सी. उदाहरण के लिए, (ω·2)² = ω·2·ω·2 = ω²·2 ≠ ω²·4.
• सही तर्क में क्रमिक घातांक सख्ती से बढ़ रहा है और निरंतर है: यदि γ > 1 और α < β, तो γ^ए <सी^बी.
• यदि α < β, तो α^सी ≤ बी^γ. उदाहरण के लिए, ध्यान दें कि 2 <3 और फिर भी 2^ω=3^ω = ω.
• यदि α > 1 और α^ख = ए^γ, तो β = γ. यदि α = 1 या α = 0 तो यह मामला नहीं है।
• सभी α और β के लिए, यदि β > 1 और α > 0 तो अद्वितीय γ, δ, और ρ मौजूद हैं जैसे कि α = β^γ·δ + ρ इस प्रकार कि 0 < δ < β और ρ < β^γ.

अर्न्स्ट जैकबस्टल ने दिखाया कि α का एकमात्र समाधान^β = β^α α≤β के साथ α=β, या α=2 और β=4 द्वारा दिए जाते हैं, या α कोई सीमा क्रमसूचक है और β=εα जहां ε एक एप्सिलॉन संख्या (गणित)|ε-से बड़ी संख्या है एक।

घातांक से परे

ऐसे क्रमिक ऑपरेशन हैं जो जोड़, गुणा और घातांक द्वारा शुरू किए गए अनुक्रम को जारी रखते हैं, जिसमें tetration, पेन्टेशन और हेक्सेशन के क्रमिक संस्करण शामिल हैं। वेब्लेन फ़ंक्शन भी देखें।

कैंटर सामान्य रूप

प्रत्येक क्रमिक संख्या α को विशिष्ट रूप से लिखा जा सकता है $\omega ^{\beta _{1}}c_{1}+\omega ^{\beta _{2}}c_{2}+\cdots +\omega ^{\beta _{k}}c_{k}$, जहां k एक प्राकृतिक संख्या है, $c_{1},c_{2},\ldots ,c_{k}$ सकारात्मक पूर्णांक हैं, और $\beta _{1}>\beta _{2}>\ldots >\beta _{k}\geq 0$ क्रमिक संख्याएँ हैं. पतित मामला α=0 तब होता है जब k=0 और कोई βs या cs नहीं होता है। α के इस अपघटन को α का 'कैंटर सामान्य रूप' कहा जाता है, और इसे आधार-ω स्थितीय अंक प्रणाली माना जा सकता है। उच्चतम प्रतिपादक $\beta _{1}$ की डिग्री कहलाती है $\alpha$, और संतुष्ट करता है $\beta _{1}\leq \alpha$. समानता $\beta _{1}=\alpha$ यदि और केवल यदि लागू होता है $\alpha =\omega ^{\alpha }$. उस स्थिति में कैंटर सामान्य रूप छोटे के संदर्भ में क्रमसूचक को व्यक्त नहीं करता है; ऐसा नीचे बताए अनुसार हो सकता है।

कैंटर सामान्य रूप का एक छोटा सा बदलाव, जिसके साथ काम करना आमतौर पर थोड़ा आसान होता है, सभी संख्याओं को सेट करना है_i 1 के बराबर और घातांक को बराबर होने दें। दूसरे शब्दों में, प्रत्येक क्रमिक संख्या α को विशिष्ट रूप से लिखा जा सकता है $\omega ^{\beta _{1}}+\omega ^{\beta _{2}}+\cdots +\omega ^{\beta _{k}}$, जहां k एक प्राकृतिक संख्या है, और $\beta _{1}\geq \beta _{2}\geq \ldots \geq \beta _{k}\geq 0$ क्रमिक संख्याएँ हैं.

कैंटर सामान्य रूप का एक और रूपांतर आधार δ विस्तार है, जहां ω को किसी भी क्रमसूचक δ>1 से प्रतिस्थापित किया जाता है, और संख्याएँ c_i δ से कम धनात्मक क्रमसूचक हैं।

कैंटर सामान्य रूप हमें विशिष्ट रूप से व्यक्त करने और आदेश देने की अनुमति देता है - ऑर्डिनल्स α जो प्राकृतिक संख्याओं से जोड़, गुणा और घातांक आधार के अंकगणितीय संचालन की एक सीमित संख्या द्वारा निर्मित होते हैं-$\omega$: दूसरे शब्दों में, मान लेना $\beta _{1}<\alpha$ कैंटर सामान्य रूप में हम घातांकों को भी व्यक्त कर सकते हैं $\beta _{i}$ कैंटर सामान्य रूप में, और के लिए वही धारणा बना रहा है $\beta _{i}$ जहाँ तक α इत्यादि का प्रश्न है, पुनरावर्ती रूप से, हमें इन अध्यादेशों के लिए अंकन की एक प्रणाली मिलती है (उदाहरण के लिए,

$\omega ^{\omega ^{\omega ^{7}\cdot 6+\omega +42}\cdot 1729+\omega ^{9}+88}\cdot 3+\omega ^{\omega ^{\omega }}\cdot 5+65537$

एक क्रमसूचक को दर्शाता है)।

क्रमसूचक ε₀ (एप्सिलॉन नंबर (गणित)) कैंटर सामान्य रूप की परिमित-लंबाई अंकगणितीय अभिव्यक्तियों के क्रमिक मूल्यों α का सेट है जो आनुवंशिक रूप से गैर-तुच्छ हैं जहां गैर-तुच्छ का अर्थ β है₁<α जब 0<α. यह सबसे छोटा क्रमसूचक है जिसमें ω के संदर्भ में कोई परिमित अंकगणितीय अभिव्यक्ति नहीं है, और सबसे छोटा क्रमवाचक ऐसा है जो $\varepsilon _{0}=\omega ^{\varepsilon _{0}}$, अर्थात कैंटर सामान्य रूप में घातांक स्वयं क्रमवाचक से छोटा नहीं होता है। यह क्रम की सीमा है

$0,\,1=\omega ^{0},\,\omega =\omega ^{1},\,\omega ^{\omega },\,\omega ^{\omega ^{\omega }},\,\ldots \,.$

क्रमसूचक ε₀ अंकगणित में विभिन्न कारणों से महत्वपूर्ण है (अनिवार्य रूप से क्योंकि यह प्रथम-क्रम तर्क की प्रमाण-सैद्धांतिक शक्ति को मापता है। प्रथम-क्रम पीनो स्वयंसिद्ध: अर्थात, पीनो के स्वयंसिद्ध ε से कम किसी भी क्रमसूचक तक ट्रांसफिनिट इंडक्शन दिखा सकते हैं।₀ लेकिन ε तक नहीं₀ अपने आप)।

कैंटर सामान्य रूप हमें योगों और क्रमादेशों के उत्पादों की गणना करने की भी अनुमति देता है: योग की गणना करने के लिए, उदाहरण के लिए, किसी को केवल जानने की जरूरत है (सूचीबद्ध गुणों को देखें) § Addition और § Multiplication) वह

$\omega ^{\beta }c+\omega ^{\beta '}c'=\omega ^{\beta '}c'\,,$

अगर $\beta '>\beta$ (अगर $\beta '=\beta$ कोई वितरणात्मक कानून को बाईं ओर लागू कर सकता है और इसे इस प्रकार फिर से लिख सकता है $\omega ^{\beta }(c+c')$, और अगर $\beta '<\beta$ अभिव्यक्ति पहले से ही कैंटर सामान्य रूप में है); और उत्पादों की गणना करने के लिए आवश्यक तथ्य यह हैं कि कब $0<\alpha =\omega ^{\beta _{1}}c_{1}+\cdots +\omega ^{\beta _{k}}c_{k}$ कैंटर सामान्य रूप में है और $0<\beta '$, तब

$\alpha \omega ^{\beta '}=\omega ^{\beta _{1}+\beta '}\,$

और

$\alpha n=\omega ^{\beta _{1}}c_{1}n+\omega ^{\beta _{2}}c_{2}+\cdots +\omega ^{\beta _{k}}c_{k}\,,$

यदि n एक गैर-शून्य प्राकृत संख्या है।

कैंटर सामान्य रूप में लिखे गए दो ऑर्डिनल्स की तुलना करने के लिए, पहले तुलना करें $\beta _{1}$, तब $c_{1}$, तब $\beta _{2}$, तब $c_{2}$, आदि.. पहले अंतर पर, जिस क्रमसूचक में बड़ा घटक होता है वह बड़ा क्रमसूचक होता है। यदि वे तब तक समान हैं जब तक एक दूसरे से पहले समाप्त नहीं हो जाता, तो जो पहले समाप्त हो जाता है वह छोटा होता है।

अभाज्य संख्याओं में गुणनखंडन

अर्न्स्ट जैकबस्टल ने दिखाया कि ऑर्डिनल्स अद्वितीय गुणनखंडन प्रमेय के एक रूप को संतुष्ट करते हैं: प्रत्येक गैर-शून्य ऑर्डिनल को अभाज्य ऑर्डिनल्स की एक सीमित संख्या के उत्पाद के रूप में लिखा जा सकता है। अभाज्य क्रम-क्रमों में यह गुणनखंडन आम तौर पर अद्वितीय नहीं है, लेकिन अभाज्यों में न्यूनतम गुणनखंडन होता है जो परिमित अभाज्य कारकों के क्रम को बदलने तक अद्वितीय होता है (Sierpiński 1958).

अभाज्य क्रमसूचक 1 से बड़ा क्रमसूचक होता है जिसे दो छोटे क्रमादेशों के गुणनफल के रूप में नहीं लिखा जा सकता। कुछ प्रथम अभाज्य संख्याएँ 2, 3, 5, ... , ω, ω+1, ω हैं²+1, ओह³+1, ..., ओ^ओह, ओह^ω+1, ω^ω+1+1, ... अभाज्य क्रमसूचक तीन प्रकार के होते हैं:

• परिमित अभाज्य संख्याएँ 2, 3, 5, ...
• फॉर्म के अध्यादेश ω^ωα किसी भी क्रमिक α के लिए। ये अभाज्य क्रमसूचक हैं जो सीमाएँ हैं, और योगात्मक रूप से अविभाज्य क्रमवाचक#गुणात्मक रूप से_अघटकक्रमांक हैं, ट्रांसफ़िनिट क्रमवाचक जो गुणन के तहत बंद होते हैं।
• फॉर्म के अध्यादेश ω^αकिसी भी क्रमिक α>0 के लिए +1। ये अनंत उत्तराधिकारी अभाज्य संख्याएँ हैं, और योगात्मक रूप से अविघटनीय क्रमवाचकों, योगात्मक रूप से अविघटनीय क्रमवाचकों के उत्तराधिकारी हैं।

अभाज्य संख्याओं में गुणनखंडन अद्वितीय नहीं है: उदाहरण के लिए, 2×3=3×2, 2×ω=ω, (ω+1)×ω=ω×ω और ω×ω^ω = ω^ω. हालाँकि, निम्नलिखित अतिरिक्त शर्तों को पूरा करने वाले अभाज्य संख्याओं में एक अद्वितीय गुणनखंडन होता है:

• प्रत्येक सीमा अभाज्य प्रत्येक उत्तराधिकारी अभाज्य से पहले होता है
• यदि अभाज्य गुणनखंड के दो लगातार अभाज्य दोनों सीमाएँ हैं या दोनों परिमित हैं, तो दूसरा वाला अधिक से अधिक पहला होता है।

इस अभाज्य गुणनखंड को कैंटर सामान्य रूप का उपयोग करके आसानी से निम्नानुसार पढ़ा जा सकता है:

• पहले क्रमसूचक को उत्पाद αβ के रूप में लिखें जहां α कैंटर सामान्य रूप में ω की सबसे छोटी शक्ति है और β एक उत्तराधिकारी है।
• यदि α=ω^γ फिर कैंटर सामान्य रूप में γ लिखने से सीमा अभाज्यों के उत्पाद के रूप में α का विस्तार मिलता है।
• अब β के कैंटर सामान्य रूप को देखें। यदि β = ω^λm + ω^μn + छोटे पद, तो β = (ω^मn + छोटे पद)(ω^λ−μ + 1)m एक छोटे क्रमसूचक और एक अभाज्य और एक पूर्णांक m का गुणनफल है। इसे दोहराने और पूर्णांकों को अभाज्यों में गुणनखंडित करने से β का अभाज्य गुणनखंडन प्राप्त होता है।

तो कैंटर का गुणनखंड सामान्य रूप से क्रमसूचक होता है

$\omega ^{\alpha _{1}}n_{1}+\cdots +\omega ^{\alpha _{k}}n_{k}$ (साथ $\alpha _{1}>\cdots >\alpha _{k}$)

अनंत अभाज्य संख्याओं और पूर्णांकों के न्यूनतम गुणनफल में है

$\omega ^{\omega ^{\beta _{1}}}\cdots \omega ^{\omega ^{\beta _{m}}}n_{k}(\omega ^{\alpha _{k-1}-\alpha _{k}}+1)n_{k-1}\cdots n_{2}(\omega ^{\alpha _{1}-\alpha _{2}}+1)n_{1}$

जहां प्रत्येक एन_i इसे इसके गुणनखंडन द्वारा परिमित अभाज्य संख्याओं के गैर-बढ़ते अनुक्रम में प्रतिस्थापित किया जाना चाहिए

$\alpha _{k}=\omega ^{\beta _{1}}+\cdots +\omega ^{\beta _{m}}$ साथ $\beta _{1}\geq \cdots \geq \beta _{m}$.

बड़े गणनीय क्रम

जैसा कि ऊपर चर्चा की गई है, नीचे दिए गए ऑर्डिनल्स का कैंटर सामान्य रूप है $\varepsilon _{0}$ इसे एक वर्णमाला में व्यक्त किया जा सकता है जिसमें केवल जोड़, गुणा और घातांक के लिए फ़ंक्शन प्रतीक, साथ ही प्रत्येक प्राकृतिक संख्या के लिए निरंतर प्रतीक शामिल हैं। $\omega$. हम केवल अचर प्रतीक 0 और उत्तराधिकारी के संचालन का उपयोग करके अनंत अनेक अंकों को हटा सकते हैं, $S$ (उदाहरण के लिए, पूर्णांक 4 को इस प्रकार व्यक्त किया जा सकता है $S(S(S(S(0))))$). यह एक क्रमसूचक संकेतन का वर्णन करता है: एक परिमित वर्णमाला पर क्रमसूचकों के नामकरण की एक प्रणाली। क्रमसूचक संकेतन की इस विशेष प्रणाली को अंकगणितीय क्रमसूचक अभिव्यक्तियों का संग्रह कहा जाता है, और यह नीचे दिए गए सभी क्रमसूचकों को व्यक्त कर सकता है $\varepsilon _{0}$, लेकिन व्यक्त नहीं कर सकता $\varepsilon _{0}$. ऐसे अन्य क्रमसूचक संकेतन हैं जो बहुत पहले के क्रमवाचकों को पकड़ने में सक्षम हैं $\varepsilon _{0}$, लेकिन क्योंकि किसी भी परिमित वर्णमाला में केवल गिनती के कई तार होते हैं, किसी भी दिए गए क्रमसूचक संकेतन के लिए नीचे क्रमवाचक होंगे $\omega _{1}$ (पहला बेशुमार क्रमसूचक) जो व्यक्त नहीं किया जा सकता। ऐसे क्रमसूचकों को बड़े गणनीय क्रमवाचकों के रूप में जाना जाता है।

जोड़, गुणा और घातांक के संचालन सभी आदिम पुनरावर्ती क्रमसूचक कार्यों के उदाहरण हैं, और अधिक सामान्य आदिम पुनरावर्ती क्रमवाचक कार्यों का उपयोग बड़े क्रमसूचकों का वर्णन करने के लिए किया जा सकता है।

प्राकृतिक संचालन

ऑर्डिनल्स पर प्राकृतिक योग और प्राकृतिक उत्पाद संचालन को 1906 में गेरहार्ड हेसेनबर्ग द्वारा परिभाषित किया गया था, और कभी-कभी इसे हेसेनबर्ग योग (या उत्पाद) भी कहा जाता है। (Sierpiński 1958). ये जॉन कॉनवे के फ़ील्ड (गणित) के अवास्तविक संख्याओं के जोड़ और गुणा (ऑर्डिनल्स तक सीमित) के समान हैं। उनका लाभ यह है कि वे साहचर्य और क्रमविनिमेय हैं, और प्राकृतिक उत्पाद प्राकृतिक योग पर वितरित होते हैं। इन परिचालनों को क्रमविनिमेय बनाने की लागत यह है कि वे सही तर्क में निरंतरता खो देते हैं, जो सामान्य योग और उत्पाद की संपत्ति है। α और β के प्राकृतिक योग को अक्सर α ⊕ β या α # β द्वारा दर्शाया जाता है, और प्राकृतिक उत्पाद को α ⊗ β या α ⨳ β द्वारा दर्शाया जाता है।

अच्छी तरह से अर्ध-आदेश के सिद्धांत में प्राकृतिक संचालन आते हैं; आदेश प्रकार (अधिकतम रैखिक आदेश) ओ (एस) और ओ (टी) के दो आंशिक आंशिक आदेश एस और टी दिए गए हैं, असंयुक्त संघ का प्रकार ओ (एस) ⊕ ओ (टी) है, जबकि प्रत्यक्ष का प्रकार उत्पाद o(S)⊗o(T) है। कोई इस संबंध को S और T को क्रमसूचक α और β चुनकर प्राकृतिक संचालन की परिभाषा के रूप में ले सकता है; इसलिए α ⊕ β, α और β के असंयुक्त संघ (आंशिक क्रम के रूप में) को विस्तारित करने वाले कुल ऑर्डर का अधिकतम ऑर्डर प्रकार है; जबकि α ⊗ β, α और β के प्रत्यक्ष उत्पाद (आंशिक ऑर्डर के रूप में) को विस्तारित करने वाले कुल ऑर्डर का अधिकतम ऑर्डर प्रकार है। इसका एक उपयोगी अनुप्रयोग तब होता है जब α और β दोनों किसी बड़े कुल क्रम के उपसमूह होते हैं; तो उनके संघ में अधिकतम α ⊕ β का ऑर्डर प्रकार होता है। यदि वे दोनों किसी क्रमित समूह के उपसमुच्चय हैं, तो उनके योग में अधिकतम α ⊗ β का क्रम प्रकार होता है।

हम α और β के प्राकृतिक योग को आगमनात्मक रूप से (α और β पर एक साथ प्रेरण द्वारा) सभी γ < β के लिए α और γ के प्राकृतिक योग से अधिक और सभी γ < α के लिए γ और β के प्राकृतिक योग से अधिक सबसे छोटे क्रमसूचक के रूप में भी परिभाषित कर सकते हैं। प्राकृतिक उत्पाद की एक आगमनात्मक परिभाषा भी है (पारस्परिक प्रेरण द्वारा), लेकिन इसे लिखना कुछ हद तक कठिन है और हम ऐसा नहीं करेंगे (उस संदर्भ में परिभाषा के लिए अतियथार्थवादी संख्याओं पर लेख देखें, जो, हालांकि, अतियथार्थवादी का उपयोग करता है घटाव, कुछ ऐसा जिसे स्पष्ट रूप से क्रमसूचकों पर परिभाषित नहीं किया जा सकता है)।

प्राकृतिक योग साहचर्य और क्रमविनिमेय है। यह हमेशा सामान्य योग से अधिक या बराबर होता है, लेकिन यह सख्ती से अधिक भी हो सकता है। उदाहरण के लिए, ω और 1 का प्राकृतिक योग ω+1 (सामान्य योग) है, लेकिन यह 1 और ω का प्राकृतिक योग भी है। प्राकृतिक उत्पाद साहचर्य और क्रमविनिमेय है और प्राकृतिक योग पर वितरित होता है। प्राकृतिक उत्पाद हमेशा सामान्य उत्पाद से अधिक या उसके बराबर होता है, लेकिन यह सख्ती से अधिक भी हो सकता है। उदाहरण के लिए, ω और 2 का प्राकृतिक उत्पाद ω·2 (सामान्य उत्पाद) है, लेकिन यह 2 और ω का प्राकृतिक उत्पाद भी है।

फिर भी दो ऑर्डिनल्स α और β के प्राकृतिक योग और उत्पाद को परिभाषित करने का एक और तरीका कैंटर सामान्य रूप का उपयोग करना है: कोई ऑर्डिनल्स का अनुक्रम पा सकता है γ₁ > ... > सी_n और दो अनुक्रम (k₁, ..., क_n) और (जे₁, ..., जे_n) प्राकृतिक संख्याएँ (शून्य सहित, लेकिन संतोषजनक क_i + जे_i > सभी के लिए 0 i) ऐसा कि

$\alpha =\omega ^{\gamma _{1}}\cdot k_{1}+\cdots +\omega ^{\gamma _{n}}\cdot k_{n}$

$\beta =\omega ^{\gamma _{1}}\cdot j_{1}+\cdots +\omega ^{\gamma _{n}}\cdot j_{n}$

और परिभाषित करें

$\alpha \#\beta =\omega ^{\gamma _{1}}\cdot (k_{1}+j_{1})+\cdots +\omega ^{\gamma _{n}}\cdot (k_{n}+j_{n}).$

प्राकृतिक जोड़ के तहत, ऑर्डिनल्स को गामा संख्याओं द्वारा उत्पन्न निःशुल्क क्रमविनिमेय मोनोइड के तत्वों से पहचाना जा सकता है ω^α. प्राकृतिक जोड़ और गुणन के तहत, ऑर्डिनल्स को डेल्टा संख्याओं द्वारा उत्पन्न मोटी हो जाओ के तत्वों से पहचाना जा सकता है।^ωα. प्राकृतिक उत्पाद के अंतर्गत अध्यादेशों में अभाज्यों में अद्वितीय गुणनखंडन नहीं होता है। जबकि पूर्ण बहुपद रिंग में अद्वितीय गुणनखंड होता है, गैर-नकारात्मक गुणांक वाले बहुपदों के उपसमुच्चय में नहीं होता है: उदाहरण के लिए, यदि x कोई डेल्टा संख्या है, तो

$x^{5}+x^{4}+x^{3}+x^{2}+x+1=(x+1)(x^{4}+x^{2}+1)=(x^{2}+x+1)(x^{3}+1)$

गैर-नकारात्मक गुणांक वाले बहुपदों के प्राकृतिक उत्पाद के रूप में दो असंगत अभिव्यक्तियाँ हैं जिन्हें आगे विघटित नहीं किया जा सकता है।

निम्बर अंकगणित

Main article: Nimber

ऑर्डिनल्स और निम्बर्स के बीच एक-से-एक पत्राचार के आधार पर ऑर्डिनल्स पर अंकगणितीय ऑपरेशन होते हैं। निम्बर्स पर तीन सामान्य ऑपरेशन निम्बर जोड़, निम्बर गुणन और मेक्स (गणित)|न्यूनतम बहिष्करण (मैक्स) हैं। निम्बर जोड़ प्राकृतिक संख्याओं पर बिटवाइज़ ऑपरेशन#XOR ऑपरेशन का सामान्यीकरण है। वह mex ऑर्डिनल्स के सेट का सबसे छोटा ऑर्डिनल है जो सेट में मौजूद नहीं है।

संदर्भ

• Thomas Jech (21 March 2006). Set Theory: The Third Millennium Edition, revised and expanded. Springer Science & Business Media. ISBN 978-3-540-44085-7.
• Kunen, Kenneth, 1980. Set Theory: An Introduction to Independence Proofs. Elsevier. ISBN 0-444-86839-9.
• Sierpiński, Wacław (1958), Cardinal and ordinal numbers, Polska Akademia Nauk Monografie Matematyczne, vol. 34, Warsaw: Państwowe Wydawnictwo Naukowe, MR 0095787

बाहरी संबंध

• ordCalc ordinal calculator