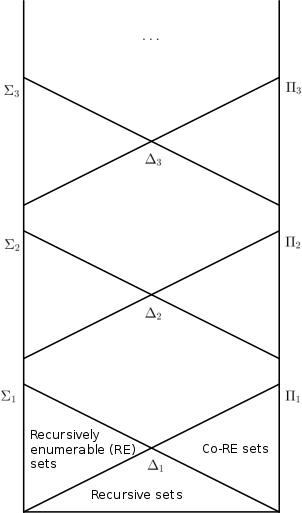
अंकगणितीय पदानुक्रम

Not to be confused with लेवी पदानुक्रम.

पदानुक्रम के स्तर कैसे इंटरैक्ट करते हैं और इसके अन्दर कुछ बुनियादी समुच्चय श्रेणियां जहाँ स्थित हैं, इसका एक उदाहरण।

गणितीय तर्क में, अंकगणितीय पदानुक्रम या क्लेन-मोस्टोव्स्की पदानुक्रम (गणितज्ञों स्टीफन कोल क्लेन और आंद्रेज मोस्टोव्स्की के बाद) सूत्र (तर्क) की जटिलता के आधार पर कुछ समुच्चय (गणित) को वर्गीकृत करता है जो उन्हें निर्धारित करता है। वर्गीकरण प्राप्त करने वाले किसी भी समुच्चय को अंकगणितीय कहा जाता है।

अंकगणितीय पदानुक्रम कम्प्यूटेबिलिटी सिद्धांत, प्रभावी वर्णनात्मक समुच्चय सिद्धांत और सिद्धांत (तर्क) अंकगणित जैसे औपचारिक सिद्धांतों के अध्ययन में महत्वपूर्ण है।

टार्स्की-कुराटोस्की एल्गोरिथम सूत्र को निर्दिष्ट वर्गीकरण और इसे परिभाषित करने वाले समुच्चय पर ऊपरी सीमा प्राप्त करने का सरल विधि प्रदान करता है।

हाइपरअरिथमेटिकल पदानुक्रम और विश्लेषणात्मक पदानुक्रम अतिरिक्त सूत्रों और समुच्चयों को वर्गीकृत करने के लिए अंकगणितीय पदानुक्रम का विस्तार करता है।

सूत्रों का अंकगणितीय पदानुक्रम

अंकगणितीय पदानुक्रम प्रथम-क्रम सिद्धांतों की भाषा में सूत्रों को वर्गीकरण प्रदान करता है प्राकृतिक संख्या n(0 सहित) के लिए वर्गीकरण कों $\Sigma _{n}^{0}$ और $\Pi _{n}^{0}$ के रूप में निरूपित करता हैं । यहां ग्रीक अक्षर लाइटफेस प्रतीक हैं, जो संकेत करता है कि सूत्रों में समुच्चय मापदण्ड नहीं हैं।

यदि सूत्र $\phi$ सामान्यतः बिना परिमाणक (तर्क) के सूत्र के सामान है, फिर $\phi$ वर्गीकरण $\Sigma _{0}^{0}$ और $\Pi _{0}^{0}$ निर्दिष्ट किया गया है . चूंकि बंधे हुए परिमाणकों वाले किसी भी सूत्र को परिबद्ध परिमाणकों वाले सूत्र से प्रतिस्थापित जा सकता है (उदाहरण के लिए, $\exists x<2\ \phi (x)$ $\phi (0)\vee \phi (1)$ के सामान है ), हम $\phi$ को सीमित परिमाणकों रखने की अनुमति भी दे सकते हैं।

वर्गीकरण $\Sigma _{n}^{0}$ और $\Pi _{n}^{0}$ निम्नलिखित नियमों का उपयोग करते हुए प्रत्येक प्राकृतिक संख्या n के लिए आगमनात्मक रूप से परिभाषित किया गया है:

• यदि $\phi$ सामान्यतः $\exists m_{1}\exists m_{2}\cdots \exists m_{k}\psi$ के सूत्र के सामान है , जहाँ $\psi$ $\Pi _{n}^{0}$ है तब $\phi$ वर्गीकरण $\Sigma _{n+1}^{0}$ दिया गया है .|
• यदि $\phi$ सामान्यतः $\forall m_{1}\forall m_{2}\cdots \forall m_{k}\psi$ के सूत्र के सामान है , जहाँ $\psi$ $\Sigma _{n}^{0}$ है , तब $\phi$ वर्गीकरण $\Pi _{n+1}^{0}$ दिया गया है .|

$\Sigma _{n}^{0}$ सूत्र एक ऐसे सूत्र के समतुल्य है जो कुछ अस्तित्वगत परिमाणक और विकल्पों के साथ प्रारंभ होता है अस्तित्वगत और सार्वभौमिक परिमाणकों की श्रृंखला के बीच $n-1$ का समय वैकल्पिक होता है; जबकि एक $\Pi _{n}^{0}$ सूत्र एक सूत्र के समतुल्य है जो कुछ सार्वभौमिक परिमाणकों से प्रारंभ होता है और समान रूप से वैकल्पिक होता है।

क्योंकि प्रत्येक प्रथम-क्रम सूत्र का सामान्य रूप है, प्रत्येक सूत्र को कम से कम वर्गीकरण निर्दिष्ट किया गया है। क्योंकि निरर्थक परिमाणकों को किसी भी सूत्र में जोड़ा जा सकता है, एक बार सूत्र को वर्गीकरण $\Sigma _{n}^{0}$ या $\Pi _{n}^{0}$ निर्दिष्ट होने के बाद इसे वर्गीकरण $\Sigma _{m}^{0}$ और $\Pi _{m}^{0}$ प्रत्येक एम > एन के लिए निर्दिष्ट किया जाएगा। इस प्रकार सूत्र को निर्दिष्ट किया गया एकमात्र प्रासंगिक वर्गीकरण सबसे कम एन वाला है; अन्य सभी वर्गीकरण इससे निर्धारित किए जा सकते हैं।

प्राकृतिक संख्याओं के समुच्चय का अंकगणितीय पदानुक्रम

प्राकृतिक संख्याओं का समुच्चय X को प्रथम-क्रम अंकगणित की भाषा में सूत्र φ द्वारा परिभाषित किया गया है (शून्य के लिए प्रतीक 0 के साथ पहली क्रम की भाषा, उत्तराधिकारी कार्य के लिए एस, + जोड़ के लिए, गुणा के लिए ×, और = समानता के लिए), यदि X के अवयव सही वही संख्याएँ हैं जो φ को संतुष्ट करती हैं। अर्थात, सभी प्राकृत संख्याओं n के लिए,

$n\in X\Leftrightarrow \mathbb {N} \models \varphi ({\underline {n}}),$

जहाँ ${\underline {n}}$ अंकगणित की भाषा में वह अंक है जिसके अनुरूप है $n$. प्रथम-क्रम अंकगणित में समुच्चय निश्चित है यदि इसे पियानो अंकगणित की भाषा में किसी सूत्र द्वारा परिभाषित किया गया है।

प्राकृतिक संख्याओं का प्रत्येक समुच्चय X जो प्रथम-क्रम अंकगणित में निश्चित है, को $\Sigma _{n}^{0}$, $\Pi _{n}^{0}$, और $\Delta _{n}^{0}$ प्रपत्र का वर्गीकरण निर्दिष्ट गया है जहाँ $n$ प्राकृतिक संख्या है, इस प्रकार है। यदि X ए द्वारा परिभाषित किया जा सकता है $\Sigma _{n}^{0}$ सूत्र तब X को वर्गीकरण $\Sigma _{n}^{0}$ निर्दिष्ट गया है . यदि X ए $\Pi _{n}^{0}$ द्वारा परिभाषित किया जा सकता है सूत्र तब X को वर्गीकरण निर्दिष्ट गया है तो X कों वर्गीकरण $\Pi _{n}^{0}$ अतिरिक्त निर्दिष्ट गया है. यदि $\Sigma _{n}^{0}$ और $\Pi _{n}^{0}$ दोनों है तब $X$ को अतिरिक्त वर्गीकरण $\Delta _{n}^{0}$.निर्दिष्ट गया है |

ध्यान दें कि $\Delta _{n}^{0}$ सूत्रों के बारे में बात करना संभवतः ही कभी समझ में आता है सूत्र; सूत्र का पहला परिमाणक या तो अस्तित्वपरक या सार्वभौमिक होता है। तो ए $\Delta _{n}^{0}$ समुच्चय अनिवार्य रूप से $\Delta _{n}^{0}$ सूत्र के अर्थ द्वारा परिभाषित नहीं है | जो $\Sigma _{n}^{0}$ और $\Pi _{n}^{0}$ किन्तु दोनों $\Sigma _{n}^{0}$ और $\Pi _{n}^{0}$ समुच्चय को परिभाषित करते हैं। उदाहरण के लिए, विषम प्राकृतिक संख्याओं का समूह $n$ $\forall k(n\neq 2\times k)$ या $\exists k(n=2\times k+1)$ द्वारा परिभाषित किया जा सकता है |

प्राकृतिक संख्याओं के समुच्चय की परिमित कार्टेशियन शक्तियों पर अंकगणितीय पदानुक्रम को परिभाषित करने के लिए समानांतर परिभाषा का उपयोग किया जाता है। मुक्त चर वाले सूत्रों के अतिरिक्त, k मुक्त संख्या चर वाले सूत्रों का उपयोग प्राकृतिक संख्याओं के k-ट्यूपल्स के समुच्चय पर अंकगणितीय पदानुक्रम को परिभाषित करने के लिए किया जाता है। ये वास्तव में युग्मन क्रिया के उपयोग से संबंधित हैं।

सापेक्ष अंकगणितीय पदानुक्रम

जिस तरह हम परिभाषित कर सकते हैं कि समुच्चय X के लिए दूसरे समुच्चय वाई के सापेक्ष पुनरावर्ती समुच्चय होने का क्या कारण है, गणना को परिभाषित करने के लिए X को ऑरेकल (कम्प्यूटेबिलिटी) के रूप में वाई से परिभाषित करने की अनुमति देकर हम इस धारणा को पूरे अंकगणितीय पदानुक्रम तक बढ़ा सकते हैं और परिभाषित कर सकते हैं कि इसका अर्थ है X के होने का कारण है वाई में, $\Sigma _{n}^{0}$, $\Delta _{n}^{0}$ या $\Pi _{n}^{0}$ क्रमशः निरूपित $\Sigma _{n}^{0,Y}$, $\Delta _{n}^{0,Y}$ और $\Pi _{n}^{0,Y}$से दर्शाया जाता है. ऐसा करने के लिए, प्राकृत संख्याओं Y का समुच्चय सही करें और प्रथम क्रम अंकगणित की भाषा में Y की सदस्यता के लिए विधेय (तर्क) जोड़ें। हम तब कहते हैं कि X $\Sigma _{n}^{0,Y}$ अंदर है यदि यह $\Sigma _{n}^{0}$ द्वारा परिभाषित किया गया है इस विस्तारित भाषा में $\Sigma _{n}^{0,Y}$ सूत्र द्वारा परिभाषित किया गया है। दूसरे शब्दों में, X$\Sigma _{n}^{0}$ है यदि यह $\Sigma _{n}^{0}$ द्वारा परिभाषित किया गया है जो Y की सदस्यता के बारे में प्रश्न पूछने के लिए सूत्र की अनुमति है। वैकल्पिक रूप से कोई $\Sigma _{n}^{0,Y}$ भी देख सकता है उन समुच्चयों के रूप में समुच्चय करता है जिन्हें Y में पुनरावर्ती समुच्चय के साथ प्रारंभ किया जा सकता है और वैकल्पिक रूप से इन समुच्चयों के संघ (समुच्चय सिद्धांत) और प्रतिच्छेदन (समुच्चय सिद्धांत) को n बार तक ले जा सकते हैं।

उदाहरण के लिए, मान लीजिए कि Y प्राकृत संख्याओं का समुच्चय है। X को Y के तत्व द्वारा विभाज्य संख्याओं का समूह होने दें। फिर X को सूत्र द्वारा परिभाषित किया गया है

$\phi (n)=\exists m\exists t(Y(m)\land m\times t=n)$ तो X $\Sigma _{1}^{0,Y}$ अंदर है (वास्तव में यह $\Delta _{0}^{0,Y}$ अंदर है भी चूंकि हम दोनों परिमाणकों को n द्वारा बाध्य कर सकते हैं)।

अंकगणित न्यूनीकरण और डिग्री

अंकगणितीय रिड्यूसिबिलिटी ट्यूरिंग न्यूनीकरण और हाइपरअरिथमेटिक रिड्यूसबिलिटी के बीच मध्यवर्ती धारणा है।

समुच्चय अंकगणितीय (अंकगणितीय और अंकगणितीय रूप से निश्चित भी) होता है यदि इसे प्रथम-क्रम अंकगणित की भाषा में किसी सूत्र द्वारा परिभाषित किया जाता है। समान रूप से X अंकगणितीय है यदि X कुछ प्राकृतिक संख्या n के लिए $\Sigma _{n}^{0}$ या $\Pi _{n}^{0}$ है। समुच्चय X 'अंकगणितीय समुच्चय Y, निरूपित है' जिसे $X\leq _{A}Y$ के रूप में चिह्नित किया जाता है , यदि X को परिभाषित किया जा सकता है, तो प्रथम-क्रम अंकगणित की भाषा में कुछ सूत्र के रूप में वाई की सदस्यता के लिए विधेय द्वारा विस्तारित किया जाता है। सामान्यतः X, Y के लिए 'अंकगणितीय रूप से कम करने योग्य' है।यदि X में है $\Sigma _{n}^{0,Y}$ या $\Pi _{n}^{0,Y}$ कुछ प्राकृतिक संख्या n के लिए $X\leq _{A}Y$ का एक समानार्थी है ।

रिश्ता $X\leq _{A}Y$ प्रतिवर्त संबंध और सकर्मक संबंध है, और इस प्रकार संबंध $\equiv _{A}$ नियम द्वारा परिभाषित किया जाता है |

$X\equiv _{A}Y\iff X\leq _{A}Y\land Y\leq _{A}X$

तुल्यता संबंध है इस संबंध के तुल्यता वर्ग अंकगणितीय डिग्री कहलाते हैं; वे आंशिक रूप से $\leq _{A}$ के अनुसार आदेश दिए गए हैं .

कैंटर और बायर अन्तरिक्ष के सबसमुच्चय का अंकगणितीय पदानुक्रम

कैंटर अन्तरिक्ष, निरूपित $2^{\omega }$, 0s और 1s के सभी अनंत क्रमों का समुच्चय है; बायर अन्तरिक्ष (समुच्चय थ्योरी), निरूपित $\omega ^{\omega }$ या ${\mathcal {N}}$, प्राकृतिक संख्याओं के सभी अनंत क्रमों का समुच्चय है। ध्यान दें कि कैंटर अन्तरिक्ष के तत्वों को प्राकृतिक संख्याओं के समुच्चय और बायर अन्तरिक्ष के तत्वों को प्राकृतिक संख्याओं से प्राकृतिक संख्याओं के कार्यों के साथ पहचाना जा सकता है।

दूसरे क्रम के अंकगणित का सामान्य स्वयंसिद्ध समुच्चय-आधारित भाषा का उपयोग करता है जिसमें समुच्चय परिमाणकों को स्वाभाविक रूप से कैंटर अन्तरिक्ष पर क्वांटिफाइंग के रूप में देखा जा सकता है। कैंटर अन्तरिक्ष के सबसमुच्चय को $\Sigma _{n}^{0}$ वर्गीकरण निर्दिष्ट गया है यदि यह एक $\Sigma _{n}^{0}$ द्वारा निश्चित है | सूत्र समुच्चय को वर्गीकरण $\Pi _{n}^{0}$ निर्दिष्ट गया है यदि यह एक $\Pi _{n}^{0}$ सूत्र द्वारा निश्चित है। यदि समुच्चय $\Sigma _{n}^{0}$ और $\Pi _{n}^{0}$ दोनों है तो इसे अतिरिक्त वर्गीकरण $\Delta _{n}^{0}$ दिया जाता है . उदाहरण के लिए, चलो $O\subset 2^{\omega }$ सभी अनंत बाइनरी स्ट्रिंग्स का समुच्चय हो जो सभी 0 नहीं हैं (या समतुल्य रूप से प्राकृतिक संख्याओं के सभी गैर-रिक्त समुच्चयों का समुच्चय) है। जैसा $O=\{X\in 2^{\omega }|\exists n(X(n)=1)\}$ हमने देखा कि $O$ ए $\Sigma _{1}^{0}$ द्वारा परिभाषित किया गया है | इसलिए $\Sigma _{1}^{0}$ निश्चित करना है।

ध्यान दें कि जब कैंटर अन्तरिक्ष के दोनों तत्व (प्राकृतिक संख्याओं के समुच्चय के रूप में माने जाते हैं) और कैंटर अन्तरिक्ष के सबसमुच्चय को अंकगणितीय पदानुक्रम में वर्गीकृत किया गया है, ये समान पदानुक्रम नहीं हैं। वास्तव में दो पदानुक्रमों के बीच का संबंध रोचक और गैर-तुच्छ है। उदाहरण के लिए $\Pi _{n}^{0}$ कैंटर अन्तरिक्ष के तत्व (सामान्यतः) तत्वों के समान नहीं हैं जिससे $X$ कैंटर अंतरिक्ष की $\{X\}$$\Pi _{n}^{0}$ है कैंटर अन्तरिक्ष का $\Pi _{n}^{0}$ सबसमुच्चय है। चूँकि, कई रोचक परिणाम दो पदानुक्रमों से संबंधित हैं।

अंकगणितीय पदानुक्रम में बेयर स्थान के उपसमुच्चय को दो विधियों से वर्गीकृत किया जा सकता है।

• बायर अन्तरिक्ष के उपसमुच्चय में मैप के अनुसार कैंटर अन्तरिक्ष का संबंधित उपसमुच्चय होता है जो प्रत्येक फलन $\omega$ को $\omega$ ग्राफ के सूचक कार्य के लिए विशेष कार्य में लिया जाता है। बेयर अन्तरिक्ष के सबसमुच्चय को वर्गीकरण $\Sigma _{n}^{1}$, $\Pi _{n}^{1}$, या $\Delta _{n}^{1}$ दिया गया है यदि और केवल यदि कैंटर अन्तरिक्ष के संबंधित उपसमुच्चय का ही वर्गीकरण है।
• दूसरे क्रम के अंकगणित के कार्यात्मक संस्करण का उपयोग करके सूत्रों के विश्लेषणात्मक पदानुक्रम को परिभाषित करके बेयर अन्तरिक्ष पर विश्लेषणात्मक पदानुक्रम की समकक्ष परिभाषा दी गई है; फिर कैंटर अन्तरिक्ष के सबसमुच्चय पर विश्लेषणात्मक पदानुक्रम को बेयर अन्तरिक्ष पर पदानुक्रम से परिभाषित किया जा सकता है। यह वैकल्पिक परिभाषा पहली परिभाषा के समान ही वर्गीकरण देती है।

समानांतर परिभाषा का उपयोग बायर अन्तरिक्ष या कैंटर अन्तरिक्ष के परिमित कार्टेशियन शक्तियों पर अंकगणितीय पदानुक्रम को परिभाषित करने के लिए किया जाता है, जिसमें कई मुक्त चर वाले सूत्रों का उपयोग किया जाता है। अंकगणितीय पदानुक्रम को किसी भी प्रभावी पोलिश स्थान पर परिभाषित किया जा सकता है; कैंटर अन्तरिक्ष और बायर अन्तरिक्ष के लिए परिभाषा विशेष रूप से सरल है क्योंकि वे साधारण दूसरे क्रम के अंकगणित की भाषा के साथ सही होते हैं।

ध्यान दें कि हम प्राकृतिक संख्याओं के कुछ समुच्चय के सापेक्ष कैंटर और बायर रिक्त स्थान के सबसमुच्चय के अंकगणितीय पदानुक्रम को भी परिभाषित कर सकते हैं। वास्तव में बोल्डफेस $\mathbf {\Sigma } _{n}^{0}$ का ही $\Sigma _{n}^{0,Y}$ संघ है प्राकृतिक संख्या वाई के सभी समुच्चयों के लिए ध्यान दें कि बोल्डफेस पदानुक्रम बोरेल पदानुक्रम का मानक पदानुक्रम है।

विस्तार और विविधताएँ

प्रत्येक पुनरावर्ती कार्य के लिए फलन प्रतीक के साथ विस्तारित भाषा का उपयोग करके सूत्रों के अंकगणितीय पदानुक्रम को परिभाषित करना संभव है। यह भिन्नता $\Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}$ के वर्गीकरण को थोड़ा बदल देती है , क्योंकि पहले क्रम के प्रथम-क्रम अंकगणित में उपयोग किया जाता है | पहले क्रम के प्रथम-क्रम अंकगणित में पुनरावर्ती कार्यों का उपयोग करने के लिए, सामान्यतः, अनंत अस्तित्वगत परिमाणकों की आवश्यकता होती है, और इस प्रकार कुछ समुच्चय जो इस परिभाषा $\Sigma _{0}^{0}$ से हैं $\Sigma _{1}^{0}$ अंदर होते हैं इस लेख की शुरुआत में दी गई परिभाषा के अनुसार $\Sigma _{1}^{0}$ और इस प्रकार पदानुक्रम में सभी उच्च वर्ग अप्रभावित रहते हैं।

प्राकृतिक संख्याओं पर सभी परिमित संबंधों पर पदानुक्रम की अधिक शब्दार्थ भिन्नता को परिभाषित किया जा सकता है; निम्नलिखित परिभाषा का प्रयोग किया जाता है। हर संगणनीय संबंध को $\Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}$ परिभाषित किया गया है . वर्गीकरण $\Sigma _{n}^{0}$ और $\Pi _{n}^{0}$ निम्नलिखित नियमों के साथ आगमनात्मक रूप से परिभाषित किया गया है।

• यदि संबंध $R(n_{1},\ldots ,n_{l},m_{1},\ldots ,m_{k})\,$ है $\Sigma _{n}^{0}$ फिर संबंध $S(n_{1},\ldots ,n_{l})=\forall m_{1}\cdots \forall m_{k}R(n_{1},\ldots ,n_{l},m_{1},\ldots ,m_{k})$ कों $\Pi _{n+1}^{0}$ परिभाषित किया गया है
• यदि संबंध $R(n_{1},\ldots ,n_{l},m_{1},\ldots ,m_{k})\,$ है $\Pi _{n}^{0}$ फिर संबंध $S(n_{1},\ldots ,n_{l})=\exists m_{1}\cdots \exists m_{k}R(n_{1},\ldots ,n_{l},m_{1},\ldots ,m_{k})$कों $\Sigma _{n+1}^{0}$ परिभाषित किया गया है

यह भिन्नता कुछ समुच्चयों के वर्गीकरण को थोड़ा बदल देती है। विशेष रूप से, $\Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}$समुच्चय के वर्ग के रूप में $\Delta _{1}^{0}$ (कक्षा में संबंधों द्वारा परिभाषित), के समान है जैसा कि पहले परिभाषित किया गया था। इसे प्राकृतिक संख्याओं, बेयर अन्तरिक्ष और कैंटर अन्तरिक्ष पर सीमित संबंधों को कवर करने के लिए बढ़ाया जा सकता है।

संकेतन का अर्थ

सूत्रों पर अंकगणितीय पदानुक्रम के लिए संकेतन से निम्नलिखित अर्थ जोड़े जा सकते हैं।

प्रतीकों में $\Sigma _{n}^{0}$ और $\Pi _{n}^{0}$ सूत्र में उपयोग किए जाने वाले सबस्क्रिप्ट $n$ सार्वभौमिक और अस्तित्वगत संख्या परिमाणकों के ब्लॉक के विकल्पों की संख्या को संकेत करता है। इसके अतिरिक्त, सबसे बाहरी ब्लॉक अस्तित्व $\Sigma _{n}^{0}$ में है सूत्र और $\Pi _{n}^{0}$ सूत्र सार्वभौमिक है।

प्रतीकों में $\Sigma _{n}^{0}$, $\Pi _{n}^{0}$, और $\Delta _{n}^{0}$ में सुपरस्क्रिप्ट $0$ परिमाणित की जा रही वस्तुओं के प्रकार को संकेत करता है। प्रकार 0 वस्तुएँ प्राकृतिक संख्याएँ हैं, और प्रकार $i+1$ की वस्तुएँ हैं ऐसे कार्य हैं जो प्रकार $i$ की वस्तुओं के समुच्चय को मैप करते हैं प्राकृतिक संख्या के लिए उच्च प्रकार की वस्तुओं पर परिमाणीकरण, जैसे कि प्राकृतिक संख्याओं से प्राकृतिक संख्याओं तक के कार्य, को 0 से अधिक सुपरस्क्रिप्ट द्वारा वर्णित किया जाता है, जैसा कि विश्लेषणात्मक पदानुक्रम में है। सुपरस्क्रिप्ट 0 संख्याओं पर क्वांटिफ़ायर संकेत करता है, सुपरस्क्रिप्ट 1 संख्याओं से संख्याओं (टाइप 1 ऑब्जेक्ट्स) के कार्यों पर क्वांटिफिकेशन संकेत करेगा, सुपरस्क्रिप्ट 2 उन कार्यों पर क्वांटिफिकेशन के अनुरूप होगा जो टाइप 1 ऑब्जेक्ट लेते हैं और नंबर लौटाते हैं,|

उदाहरण

• $\Sigma _{1}^{0}$ h> संख्याओं के समुच्चय वे हैं जिन्हें प्रपत्र के $\exists n_{1}\cdots \exists n_{k}\psi (n_{1},\ldots ,n_{k},m)$ सूत्र द्वारा परिभाषित किया जा सकता है जहाँ $\psi$ केवल परिबद्ध परिमाणक हैं। ये केवल पुनरावर्ती गणना योग्य समुच्चय हैं।
• प्राकृतिक संख्याओं का समुच्चय जो कुल कार्यों की गणना करने वाली ट्यूरिंग मशीनों के लिए $\Pi _{2}^{0}$ सूचकांक हैं . सामान्यतः, एक संकेत $e$ यदि और केवल यदि प्रत्येक के लिए इस समुच्चय में आता है $m$ वहाँ है एक $s$ जैसे कि ट्यूरिंग मशीन संकेत $e$ इनपुट पर रुक जाता है | $m$ बाद $s$ कदम" एक पूर्ण प्रमाण यह दिखाएगा कि पिछले वाक्य में उद्धरण चिह्नों में प्रदर्शित संपत्ति किसके द्वारा प्रथम-क्रम $\Sigma _{1}^{0}$ सूत्र अंकगणित की भाषा में निश्चित है।
• प्रत्येक $\Sigma _{1}^{0}$ बेयर अन्तरिक्ष या कैंटर अन्तरिक्ष का सबसमुच्चय अन्तरिक्ष पर सामान्य टोपोलॉजी में खुला समुच्चय है। इसके अतिरिक्त, ऐसे किसी भी समुच्चय के लिए बुनियादी खुले समुच्चयों के गोडेल नंबरों की संगणनीय गणना है जिसका संघ मूल समुच्चय है। इस कारण से, $\Sigma _{1}^{0}$ समुच्चय को कभी-कभी प्रभावी रूप से खुला कहा जाता है। इसी तरह, हर $\Pi _{1}^{0}$ समुच्चय बंद है और $\Pi _{1}^{0}$ समुच्चय को कभी-कभी प्रभावी रूप से बंद कहा जाता है।
• कैंटर अन्तरिक्ष या बेयर अन्तरिक्ष का हर अंकगणितीय उपसमुच्चय बोरेल समुच्चय है। लाइटफेस बोरेल पदानुक्रम अतिरिक्त बोरेल समुच्चयों को सम्मिलित करने के लिए अंकगणितीय पदानुक्रम का विस्तार करता है। उदाहरण के लिए, हर $\Pi _{2}^{0}$ कैंटर या बेयर अन्तरिक्ष का सबसमुच्चय है a $G_{\delta }$ समुच्चय (अर्थात, समुच्चय जो कई खुले समुच्चयों के प्रतिच्छेदन के सामान है)। इसके अतिरिक्त, इनमें से प्रत्येक खुला समुच्चय $\Sigma _{1}^{0}$ है और इन खुले समुच्चयों के गोडेल नंबरों की सूची में संगणनीय गणना है। यदि $\phi (X,n,m)$ है $\Sigma _{0}^{0}$ फ्री समुच्चय वेरिएबल X और फ्री नंबर वेरिएबल्स के साथ $n,m$ फिर $\Pi _{2}^{0}$ इसका $\{X\mid \forall n\exists m\phi (X,n,m)\}$ का प्रतिक्षेदन है | $\Sigma _{1}^{0}$ के समुच्चय $\{X\mid \exists m\phi (X,n,m)\}$ n के रूप में प्राकृतिक संख्याओं के समुच्चय पर होता है।
• $\Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}$ h> सूत्रों को एक-एक करके सभी स्थितियों पर जाकर जाँच की जा सकती है, जो संभव है क्योंकि उनके सभी परिमाणकों बंधे हुए हैं। इसके लिए समय उनके तर्कों में बहुपद है (उदाहरण के लिए n में बहुपद $\varphi (n)$); इस प्रकार उनकी संबंधित निर्णय समस्याएं ई (जटिलता) में सम्मिलित हैं (क्योंकि एन बिट्स की संख्या में घातीय है)। यह अब वैकल्पिक परिभाषाओं के अनुसार नहीं है , जो $\Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}$ पुनरावर्ती कार्यों के उपयोग की अनुमति देता है, क्योंकि अब परिमाणक तर्कों के किसी भी पुनरावर्ती कार्य से बंधे हो सकते हैं।
• $\Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}$ h> वैकल्पिक परिभाषा के अनुसार सूत्र, जो परिबद्ध परिमाणकों के साथ पुनरावर्ती कार्यों के उपयोग की अनुमति देता है, प्रपत्र की प्राकृतिक संख्याओं के समुच्चय के अनुरूप होता है $\{n:f(n)=0\}$ पुनरावर्ती क्रिया के लिए f. ऐसा इसलिए है क्योंकि परिबद्ध परिमाणकों की अनुमति परिभाषा में कुछ भी नहीं जोड़ती है: पुनरावर्ती f के लिए, $\forall k<n:f(k)=0$ वैसा ही है जैसा कि $f(0)+f(1)+...f(n)=0$, और $\exists k<n:f(k)=0$ वैसा ही है जैसा कि $f(0)*f(1)*...f(n)=0$; कोर्स-ऑफ़-वैल्यू रिकर्सन के साथ इनमें से प्रत्येक को रिकर्सन फलन द्वारा परिभाषित किया जा सकता है।

गुण

निम्नलिखित गुण प्राकृतिक संख्याओं के समुच्चय के अंकगणितीय पदानुक्रम और कैंटर या बायर अन्तरिक्ष के सबसमुच्चय के अंकगणितीय पदानुक्रम के लिए हैं।

• संग्रह $\Pi _{n}^{0}$ और $\Sigma _{n}^{0}$ उनके संबंधित तत्वों के परिमित संघ (समुच्चय सिद्धांत) और परिमित चौराहे (समुच्चय सिद्धांत) के अनुसार बंद हैं।
• समुच्चय $\Sigma _{n}^{0}$ है यदि और केवल यदि इसका पूरक $\Pi _{n}^{0}$ है . एक समुच्चय $\Delta _{n}^{0}$ है यदि और केवल यदि समुच्चय दोनों $\Sigma _{n}^{0}$ और $\Pi _{n}^{0}$ है , ऐसे में इसका पूरक $\Delta _{n}^{0}$ भी होगा |
• समावेशन $\Pi _{n}^{0}\subsetneq \Pi _{n+1}^{0}$ और $\Sigma _{n}^{0}\subsetneq \Sigma _{n+1}^{0}$ सभी के लिए पकड़ो $n$. इस प्रकार पदानुक्रम का पतन नहीं होता है। यह पद के प्रमेय का सीधा परिणाम है।
• समावेशन $\Delta _{n}^{0}\subsetneq \Pi _{n}^{0}$, $\Delta _{n}^{0}\subsetneq \Sigma _{n}^{0}$ और $\Sigma _{n}^{0}\cup \Pi _{n}^{0}\subsetneq \Delta _{n+1}^{0}$ इसके लिए $n\geq 1$ रखें |

* उदाहरण के लिए, सार्वभौमिक ट्यूरिंग मशीन T के लिए, जोड़े (एन, एम) का समुच्चय ऐसा है कि T एन पर रुकता है किन्तु एम पर नहीं $\Delta _{2}^{0}$, में है (रोकथाम की समस्या के लिए दैवज्ञ के साथ संगणनीय होना) किन्तु $\Sigma _{1}^{0}\cup \Pi _{1}^{0}$ अंदर नहीं है |, .

• इस आलेख में दी गई परिभाषा से समावेश सख्त है, किन्तु $\Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}=\Sigma _{0}^{0}\cup \Pi _{0}^{0}\subset \Delta _{1}^{0}$ पहचान के साथ $\Delta _{1}^{0}$ परिभाषा अंकगणितीय पदानुक्रम विस्तार और विविधताओं में से एक के अंतर्गत रखती है।

ट्यूरिंग मशीनों से संबंध

See also: पद प्रमेय

संगणनीय समुच्चय

यदि S संगणनीय फलन कम्प्यूटेबल समुच्चय और संबंध है, तो S और इसका पूरक (समुच्चय सिद्धांत) दोनों पुनरावर्ती रूप से गणना योग्य हैं (यदि T ट्यूरिंग मशीन है जो S और 0 में इनपुट के लिए 1 दे रही है, तो हम ट्यूरिंग मशीन बना सकते हैं जो केवल रुकेगी पूर्व पर, और दूसरा केवल बाद वाले पर रुकता है)।

पद प्रमेय के अनुसार, S और इसका पूरक दोनों अंदर $\Sigma _{1}^{0}$ हैं . इसका कारण है कि S दोनों अंदर $\Sigma _{1}^{0}$ है और इसलिए $\Pi _{1}^{0}$,में यह अंदर $\Delta _{1}^{0}$ है .

इसी प्रकार, प्रत्येक समुच्चय के लिए S में $\Delta _{1}^{0}$, S और इसके पूरक दोनों अंदर $\Sigma _{1}^{0}$ हैं और इसलिए (पद के प्रमेय द्वारा) कुछ ट्यूरिंग मशीनों T₁ और T₂ द्वारा पुनरावर्ती रूप से गणना योग्य हैं, क्रमश। प्रत्येक संख्या n के लिए, इनमें से सही एक रुकता है। इसलिए हम ट्यूरिंग मशीन T का निर्माण कर सकते हैं जो T₁ और T₂ के बीच वैकल्पिक है, रुकना और 1 जब पूर्व रुकता है या रुकता है और 0 लौटता है जब बाद वाला रुकता है। इस प्रकार T हर n पर रुकता है और लौटता है कि क्या यह S में है, तो S संगणनीय है।

मुख्य परिणामों का सारांश

प्राकृतिक संख्याओं के ट्यूरिंग कम्प्यूटेशनल समुच्चय केवल $\Delta _{1}^{0}$ स्तर पर समुच्चय होते हैं अंकगणितीय पदानुक्रम का पुनरावर्ती गणना योग्य समुच्चय केवल स्तर पर समुच्चय $\Sigma _{1}^{0}$ होते हैं .

कोई भी ओरेकल मशीन अपनी स्वयं की हॉल्टिंग समस्या को हल करने में सक्षम नहीं है (ट्यूरिंग के प्रमाण की भिन्नता प्रयुक्त होती है)। ए के लिए रुकने की समस्या $\Delta _{n}^{0,Y}$ ऑरैकल वास्तव में $\Sigma _{n+1}^{0,Y}$ बैठता है .

पद प्रमेय प्राकृतिक संख्याओं के समुच्चय के अंकगणितीय पदानुक्रम और ट्यूरिंग डिग्री के बीच घनिष्ठ संबंध स्थापित करता है। विशेष रूप से, यह सभी n ≥ 1 के लिए निम्नलिखित तथ्य स्थापित करता है:

• समुच्चय $\emptyset ^{(n)}$ (खाली समुच्चय का nवां ट्यूरिंग कूदो ) $\Sigma _{n}^{0}$ कई-एक पूर्ण है |
• समुच्चय $\mathbb {N} \setminus \emptyset ^{(n)}$ $\Pi _{n}^{0}$ अनेक-एक में पूर्ण है .
• समुच्चय $\emptyset ^{(n-1)}$ $\Delta _{n}^{0}$ ट्यूरिंग पूरा समुच्चय है .

बहुपद पदानुक्रम अंकगणितीय पदानुक्रम का व्यवहार्य संसाधन-सीमित संस्करण है जिसमें सम्मिलित संख्याओं पर बहुपद लंबाई सीमाएँ रखी जाती हैं (या, समतुल्य, बहुपद समय सीमा सम्मिलित ट्यूरिंग मशीनों पर रखी जाती है)। यह प्राकृतिक संख्याओं के कुछ समुच्चयों का उत्तम वर्गीकरण देता है जो अंकगणितीय पदानुक्रम का $\Delta _{1}^{0}$ स्तर पर हैं।

अन्य पदानुक्रमों से संबंध

Lightface		Boldface
Σ0 0 = Π0 0 = Δ0 0 (sometimes the same as Δ0 1)		Σ0 0 = Π0 0 = Δ0 0 (if defined)
Δ0 1 = recursive		Δ0 1 = clopen
Σ0 1 = recursively enumerable	Π0 1 = co-recursively enumerable	Σ0 1 = G = open	Π0 1 = F = closed
Δ0 2		Δ0 2
Σ0 2	Π0 2	Σ0 2 = Fσ	Π0 2 = Gδ
Δ0 3		Δ0 3
Σ0 3	Π0 3	Σ0 3 = Gδσ	Π0 3 = Fσδ
⋮		⋮
Σ0 <ω = Π0 <ω = Δ0 <ω = Σ1 0 = Π1 0 = Δ1 0 = arithmetical		Σ0 <ω = Π0 <ω = Δ0 <ω = Σ1 0 = Π1 0 = Δ1 0 = boldface arithmetical
⋮		⋮
Δ0 α (α recursive)		Δ0 α (α countable)
Σ0 α	Π0 α	Σ0 α	Π0 α
⋮		⋮
Σ0 ωCK 1 = Π0 ωCK 1 = Δ0 ωCK 1 = Δ1 1 = hyperarithmetical		Σ0 ω1 = Π0 ω1 = Δ0 ω1 = Δ1 1 = B = Borel
Σ1 1 = lightface analytic	Π1 1 = lightface coanalytic	Σ1 1 = A = analytic	Π1 1 = CA = coanalytic
Δ1 2		Δ1 2
Σ1 2	Π1 2	Σ1 2 = PCA	Π1 2 = CPCA
Δ1 3		Δ1 3
Σ1 3	Π1 3	Σ1 3 = PCPCA	Π1 3 = CPCPCA
⋮		⋮
Σ1 <ω = Π1 <ω = Δ1 <ω = Σ2 0 = Π2 0 = Δ2 0 = analytical		Σ1 <ω = Π1 <ω = Δ1 <ω = Σ2 0 = Π2 0 = Δ2 0 = P = projective
⋮		⋮

यह भी देखें

• विश्लेषणात्मक पदानुक्रम
• लेवी पदानुक्रम
• पदानुक्रम (गणित)
• व्याख्यात्मक तर्क
• बहुपद पदानुक्रम

संदर्भ

• Japaridze, Giorgie (1994), "The logic of arithmetical hierarchy", Annals of Pure and Applied Logic, 66 (2): 89–112, doi:10.1016/0168-0072(94)90063-9, Zbl 0804.03045.
• Moschovakis, Yiannis N. (1980), Descriptive Set Theory, Studies in Logic and the Foundations of Mathematics, vol. 100, North Holland, ISBN 0-444-70199-0, Zbl 0433.03025.
• Nies, André (2009), Computability and randomness, Oxford Logic Guides, vol. 51, Oxford: Oxford University Press, ISBN 978-0-19-923076-1, Zbl 1169.03034.
• Rogers, H., Jr. (1967), Theory of recursive functions and effective computability, Maidenhead: McGraw-Hill, Zbl 0183.01401.