अनुरूप मानचित्र

एक अनुरूप मानचित्र के नीचे एक आयताकार ग्रिड (शीर्ष) और उसकी छवि

f

(तल)। ऐसा देखा गया है

f

90° पर प्रतिच्छेद करने वाली रेखाओं के युग्मों को 90° पर अभी भी प्रतिच्छेद करने वाले वक्रों के युग्मों को मानचित्रित करता है।

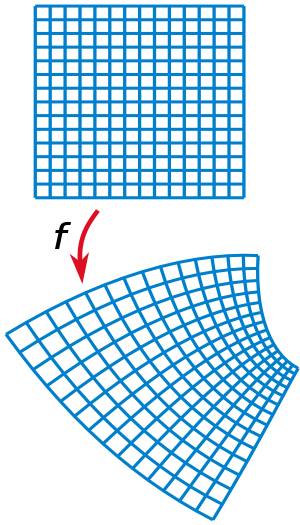
गणित में, एक अनुरूप मानचित्र एक फ़ंक्शन (गणित) है जो स्थानीय रूप से कोणों को संरक्षित करता है, लेकिन आवश्यक रूप से लंबाई को नहीं।

अधिक औपचारिक रूप से, आइए $U$ और $V$ के खुले उपसमुच्चय हों $\mathbb {R} ^{n}$ . एक समारोह $f:U\to V$ किसी बिंदु पर अनुरूप (या कोण-संरक्षण) कहा जाता है $u_{0}\in U$ यदि यह निर्देशित वक्रों के बीच कोणों को संरक्षित करता है $u_{0}$ , साथ ही अभिविन्यास को संरक्षित करना। अनुरूप मानचित्र अनंत रूप से छोटी आकृतियों के कोण और आकार दोनों को संरक्षित करते हैं, लेकिन जरूरी नहीं कि उनका आकार या वक्रता हो।

अनुरूप संपत्ति को जैकोबियन मैट्रिक्स और समन्वय परिवर्तन के निर्धारक व्युत्पन्न मैट्रिक्स के संदर्भ में वर्णित किया जा सकता है। जब भी प्रत्येक बिंदु पर जैकोबियन एक रोटेशन मैट्रिक्स (निर्धारक के साथ ऑर्थोगोनल मैट्रिक्स) का एक सकारात्मक स्केलर होता है, तो परिवर्तन अनुरूप होता है। कुछ लेखक ओरिएंटेशन-रिवर्सिंग मैपिंग को शामिल करने के लिए अनुरूपता को परिभाषित करते हैं जिनके जैकोबियन को किसी भी ऑर्थोगोनल मैट्रिक्स के स्केलर समय के रूप में लिखा जा सकता है।^[1] दो आयामों में मैपिंग के लिए, (अभिविन्यास-संरक्षण) अनुरूप मैपिंग वास्तव में स्थानीय रूप से उलटा होलोमोर्फिक फ़ंक्शन फ़ंक्शन हैं। तीन और उच्चतर आयामों में, लिउविले का प्रमेय (अनुरूप मानचित्रण)|लिउविले का प्रमेय तेजी से अनुरूप मानचित्रण को कुछ प्रकारों तक सीमित करता है।

अनुरूपता की धारणा रीमैनियन मैनिफोल्ड या अर्ध-रीमैनियन मैनिफोल्ड के बीच मानचित्रों के लिए स्वाभाविक तरीके से सामान्यीकृत होती है।

दो आयामों में

अगर $U$ जटिल तल का एक खुला सेट है $\mathbb {C}$ , फिर एक फ़ंक्शन (गणित) $f:U\to \mathbb {C}$ अनुरूप है यदि और केवल यदि यह होलोमोर्फिक फ़ंक्शन है और इसका व्युत्पन्न हर जगह गैर-शून्य है $U$ . अगर $f$ एंटीहोलोमॉर्फिक फ़ंक्शन (एक होलोमोर्फिक फ़ंक्शन से जटिल संयुग्म) है, यह कोणों को संरक्षित करता है लेकिन उनके अभिविन्यास को उलट देता है।

साहित्य में, अनुरूपता की एक और परिभाषा है: एक मानचित्रण $f$ जो समतल में एक खुले सेट पर एक-से-एक और होलोमोर्फिक है। ओपन मैपिंग प्रमेय व्युत्क्रम फ़ंक्शन को बाध्य करता है (की छवि पर परिभाषित)। $f$ ) होलोमोर्फिक होना। इस प्रकार, इस परिभाषा के तहत, एक नक्शा अनुरूप है यदि और केवल यदि वह बायोलोमोर्फिक है। अनुरूप मानचित्रों की दो परिभाषाएँ समतुल्य नहीं हैं। एक-से-एक और होलोमोर्फिक होने का तात्पर्य गैर-शून्य व्युत्पन्न होना है। हालाँकि, घातीय फ़ंक्शन एक गैर-शून्य व्युत्पन्न के साथ एक होलोमोर्फिक फ़ंक्शन है, लेकिन यह आवधिक होने के कारण एक-से-एक नहीं है।^[2] रीमैन मानचित्रण प्रमेय, जटिल विश्लेषण के गहन परिणामों में से एक, बताता है कि कोई भी गैर-रिक्त खुला बस उचित उपसमुच्चय से जुड़ा होता है $\mathbb {C}$ खुली इकाई डिस्क में एक आक्षेप अनुरूप मानचित्र स्वीकार करता है $\mathbb {C}$ . अनौपचारिक रूप से, इसका मतलब यह है कि किसी भी बूँद को कुछ अनुरूप मानचित्र द्वारा एक पूर्ण वृत्त में परिवर्तित किया जा सकता है।

रीमैन क्षेत्र पर वैश्विक अनुरूप मानचित्र

रीमैन क्षेत्र प्रक्षेपण का एक नक्शा स्वयं अनुरूप है यदि और केवल यदि यह मोबियस परिवर्तन है।

मोबियस परिवर्तन का जटिल संयुग्म कोणों को संरक्षित करता है, लेकिन अभिविन्यास को उलट देता है। उदाहरण के लिए, व्युत्क्रम ज्यामिति#वृत्त व्युत्क्रम।

तीन प्रकार के कोणों के संबंध में अनुरूपता

समतल ज्यामिति में तीन प्रकार के कोण होते हैं जिन्हें एक अनुरूप मानचित्र में संरक्षित किया जा सकता है।^[3] प्रत्येक को अपने स्वयं के वास्तविक बीजगणित, सामान्य जटिल संख्याओं, विभाजित-जटिल संख्याओं और दोहरी संख्याओं द्वारा होस्ट किया जाता है। अनुरूप मानचित्रों का वर्णन प्रत्येक मामले में रैखिक भिन्नात्मक परिवर्तन#अनुरूप संपत्ति द्वारा किया जाता है।^[4]

तीन या अधिक आयामों में

रीमैनियन ज्यामिति

रीमानियन ज्यामिति में, दो रीमैनियन मीट्रिक $g$ और $h$ एक चिकने मैनिफ़ोल्ड पर $M$ अनुरूप समतुल्य कहलाते हैं यदि $g=uh$ किसी सकारात्मक कार्य के लिए $u$ पर $M$ . कार्यक्रम $u$ अनुरूप कारक कहा जाता है।

यदि खींची गई मीट्रिक मूल रूप से मूल के बराबर है, तो दो रीमैनियन मैनिफोल्ड्स के बीच एक भिन्नता को एक अनुरूप मानचित्र कहा जाता है। उदाहरण के लिए, समतल पर एक गोले का त्रिविम प्रक्षेपण (गणित) अनंत पर एक बिंदु के साथ संवर्धित एक अनुरूप मानचित्र है।

कोई भी अनुरूप रूप से समतुल्य रीमैनियन मेट्रिक्स के एक वर्ग के रूप में, एक चिकनी मैनिफोल्ड पर एक अनुरूप संरचना को परिभाषित कर सकता है।

यूक्लिडियन स्थान

जोसेफ लिउविले के लिउविले प्रमेय (अनुरूप मानचित्रण) से पता चलता है कि दो आयामों की तुलना में उच्च आयामों में बहुत कम अनुरूप मानचित्र हैं। यूक्लिडियन अंतरिक्ष के एक खुले उपसमुच्चय से आयाम तीन या उससे अधिक के समान यूक्लिडियन स्थान में कोई भी अनुरूप मानचित्र तीन प्रकार के परिवर्तनों से बना हो सकता है: एक समरूप परिवर्तन, एक आइसोमेट्री, और एक विशेष अनुरूप परिवर्तन।

अनुप्रयोग

अनुरूप मानचित्रण के अनुप्रयोग मौजूद हैं एयरोस्पेस इंजीनियरिंग में,^[5] बायोमेडिकल विज्ञान में^[6] (ब्रेन मैपिंग सहित^[7] और आनुवंशिक मानचित्रण^[8]^[9]^[10]), अनुप्रयुक्त गणित में (जियोडेसिक्स के लिए^[11] और ज्यामिति में^[12]), पृथ्वी विज्ञान में (भूभौतिकी सहित,^[13] भूगोल,^[14] और कार्टोग्राफी),^[15] इंजीनियरिंग में,^[16]^[17] और इलेक्ट्रॉनिक्स में.^[18]

मानचित्रकला

नक्शानवीसी में, मर्केटर प्रक्षेपण और स्टीरियोग्राफिक प्रोजेक्शन सहित कई नामित मानचित्र प्रक्षेपण अनुरूप हैं। वे समुद्री नेविगेशन में उपयोग के लिए विशेष रूप से उपयोगी हैं क्योंकि किसी भी निरंतर दिशा को एक सीधे खंड के रूप में प्रस्तुत करने की उनकी अनूठी संपत्ति है। ऐसा मार्ग, जिसे रंब (या, गणितीय रूप से, लॉक्सोड्रोम) के रूप में जाना जाता है, समुद्री नेविगेशन में पसंद किया जाता है क्योंकि जहाज निरंतर कम्पास दिशा में चल सकते हैं।

भौतिकी और इंजीनियरिंग

इंजीनियरिंग और भौतिकी में समस्याओं को हल करने के लिए अनुरूप मानचित्रण अमूल्य हैं जिन्हें एक जटिल चर के कार्यों के संदर्भ में व्यक्त किया जा सकता है, फिर भी असुविधाजनक ज्यामिति प्रदर्शित होती हैं। एक उपयुक्त मैपिंग चुनकर, विश्लेषक असुविधाजनक ज्यामिति को अधिक सुविधाजनक में बदल सकता है। उदाहरण के लिए, कोई व्यक्ति विद्युत क्षेत्र की गणना करना चाह सकता है, $E(z)$ , एक निश्चित कोण (जहाँ) द्वारा अलग किए गए दो संवाहक विमानों के कोने के पास स्थित एक बिंदु आवेश से उत्पन्न होता है $z$ 2-स्पेस में एक बिंदु का जटिल निर्देशांक है)। यह समस्या बंद रूप में हल करने में काफी अनाड़ी है। हालाँकि, एक बहुत ही सरल अनुरूप मानचित्रण को नियोजित करके, असुविधाजनक कोण को सटीक रूप से मैप किया जाता है $\pi$ रेडियंस, जिसका अर्थ है कि दो तलों का कोना एक सीधी रेखा में परिवर्तित हो जाता है। इस नए डोमेन में, समस्या (एक संचालन दीवार के पास स्थित एक बिंदु चार्ज से प्रभावित विद्युत क्षेत्र की गणना करने की) को हल करना काफी आसान है। इस डोमेन में समाधान प्राप्त होता है, $E(w)$ , और फिर उसे नोट करके मूल डोमेन पर वापस मैप किया गया $w$ एक फ़ंक्शन के रूप में प्राप्त किया गया था (अर्थात, फ़ंक्शन संरचना $E$ और $w$ ) का $z$ , कहाँ से $E(w)$ के रूप में देखा जा सकता है $E(w(z))$ , जो का एक कार्य है $z$ , मूल समन्वय आधार। ध्यान दें कि यह एप्लिकेशन इस तथ्य का खंडन नहीं करता है कि अनुरूप मानचित्रण कोणों को संरक्षित करते हैं, वे ऐसा केवल अपने डोमेन के आंतरिक बिंदुओं के लिए करते हैं, सीमा पर नहीं। एक अन्य उदाहरण टैंकों में स्लोश गतिशीलता की सीमा मूल्य समस्या को हल करने के लिए अनुरूप मानचित्रण तकनीक का अनुप्रयोग है।^[19] यदि कोई फ़ंक्शन हार्मोनिक फ़ंक्शन है (अर्थात, यह लाप्लास के समीकरण को संतुष्ट करता है $\nabla ^{2}f=0$ ) एक समतल डोमेन (जो द्वि-आयामी है) पर, और एक अनुरूप मानचित्र के माध्यम से दूसरे समतल डोमेन में परिवर्तित हो जाता है, परिवर्तन भी हार्मोनिक है। इस कारण से, कोई भी फ़ंक्शन जो किसी क्षमता द्वारा परिभाषित किया गया है, उसे एक अनुरूप मानचित्र द्वारा रूपांतरित किया जा सकता है और फिर भी एक क्षमता द्वारा नियंत्रित किया जा सकता है। संभावित द्वारा परिभाषित समीकरणों के भौतिकी में उदाहरणों में विद्युत चुम्बकीय क्षेत्र, गुरुत्वाकर्षण क्षेत्र और, द्रव गतिशीलता में, संभावित प्रवाह शामिल है, जो निरंतर घनत्व, शून्य चिपचिपाहट और अघूर्णी सदिश क्षेत्र मानते हुए द्रव प्रवाह का एक अनुमान है। एक अनुरूप मानचित्र के तरल गतिशील अनुप्रयोग का एक उदाहरण जौकोव्स्की परिवर्तन है जिसका उपयोग जौकोव्स्की एयरफ़ोइल के चारों ओर प्रवाह के क्षेत्र की जांच करने के लिए किया जा सकता है।

कुछ विशिष्ट ज्यामितियों में अरेखीय आंशिक अंतर समीकरणों को हल करने में अनुरूप मानचित्र भी मूल्यवान हैं। ऐसे विश्लेषणात्मक समाधान गवर्निंग समीकरण के संख्यात्मक सिमुलेशन की सटीकता पर एक उपयोगी जांच प्रदान करते हैं। उदाहरण के लिए, अर्ध-अनंत दीवार के चारों ओर बहुत चिपचिपी मुक्त-सतह प्रवाह के मामले में, डोमेन को आधे-तल पर मैप किया जा सकता है जिसमें समाधान एक-आयामी और गणना करने में आसान होता है।^[20] असतत प्रणालियों के लिए, नौरी और यांग ने ज्यामिति (उर्फ व्युत्क्रम ज्यामिति ) में एक अच्छी तरह से ज्ञात अनुरूप मानचित्रण के माध्यम से असतत सिस्टम रूट लोकस को निरंतर रूट लोकस में परिवर्तित करने का एक तरीका प्रस्तुत किया।^[21]

मैक्सवेल के समीकरण

मैक्सवेल के समीकरण लोरेंत्ज़ परिवर्तनों द्वारा संरक्षित हैं जो गोलाकार और हाइपरबोलिक घुमावों सहित एक समूह बनाते हैं। उत्तरार्द्ध को कभी-कभी वृत्ताकार घुमावों से अलग करने के लिए लोरेंत्ज़ बूस्ट कहा जाता है। ये सभी परिवर्तन अनुरूप हैं क्योंकि हाइपरबोलिक घुमाव अतिपरवलयिक कोण (जिसे तेज़ी कहा जाता है) को संरक्षित करते हैं और अन्य घुमाव कोण को संरक्षित करते हैं। पोंकारे समूह में अनुवादों की शुरूआत फिर से कोणों को संरक्षित करती है।

मैक्सवेल के समीकरणों के संबंधित समाधानों के लिए अनुरूप मानचित्रों के एक बड़े समूह की पहचान एबेनेज़र कनिंघम (1908) और हैरी बेटमैन (1910) द्वारा की गई थी। कैम्ब्रिज विश्वविद्यालय में उनके प्रशिक्षण ने उन्हें छवि आवेश की विधि और गोले और व्युत्क्रम के लिए छवियों के संबंधित तरीकों की सुविधा प्रदान की थी। जैसा कि एंड्रयू वारविक (2003) मास्टर्स ऑफ थ्योरी द्वारा बताया गया है: ^[22]

प्रत्येक चार-आयामी समाधान को छद्म-त्रिज्या के चार-आयामी हाइपर-गोले में उलटा किया जा सकता है

K

एक नया समाधान तैयार करने के लिए.

वारविक ने सापेक्षता के इस नए प्रमेय को आइंस्टीन की कैम्ब्रिज प्रतिक्रिया के रूप में उजागर किया है, और व्युत्क्रम की विधि का उपयोग करके अभ्यास पर स्थापित किया है, जैसे कि जेम्स हॉपवुड जीन्स की पाठ्यपुस्तक विद्युत और चुंबकत्व के गणितीय सिद्धांत में पाया गया है।

सामान्य सापेक्षता

सामान्य सापेक्षता में, अनुरूप मानचित्र सबसे सरल और इस प्रकार सबसे सामान्य प्रकार के कारण परिवर्तन हैं। भौतिक रूप से, ये अलग-अलग ब्रह्मांडों का वर्णन करते हैं जिनमें सभी समान घटनाएं और इंटरैक्शन अभी भी (कारण रूप से) संभव हैं, लेकिन इसे प्रभावित करने के लिए एक नया अतिरिक्त बल आवश्यक है (अर्थात, सभी समान प्रक्षेपवक्रों की प्रतिकृति के लिए जियोडेसिक गति से प्रस्थान की आवश्यकता होगी क्योंकि मीट्रिक टेंसर (सामान्य सापेक्षता) अलग है)। इसका उपयोग अक्सर गुरुत्वाकर्षण विलक्षणता से परे विस्तार के लिए मॉडल बनाने की कोशिश करने के लिए किया जाता है, उदाहरण के लिए महा विस्फोट से पहले भी ब्रह्मांड के विवरण की अनुमति देने के लिए।

यह भी देखें

बिहोलोमोर्फिक मानचित्र
कैराथोडोरी का प्रमेय (अनुरूप मानचित्रण)|कैराथोडोरी का प्रमेय - एक अनुरूप मानचित्र लगातार सीमा तक फैला होता है
पेनरोज़ आरेख
श्वार्ज़-क्रिस्टोफ़ेल मानचित्रण - एक साधारण बहुभुज के आंतरिक भाग पर ऊपरी आधे तल का एक अनुरूप परिवर्तन
विशेष रैखिक समूह - परिवर्तन जो आयतन (कोणों के विपरीत) और अभिविन्यास को संरक्षित करते हैं

संदर्भ

↑ Blair, David (2000-08-17). उलटा सिद्धांत और अनुरूप मानचित्रण. The Student Mathematical Library. Vol. 9. Providence, Rhode Island: American Mathematical Society. doi:10.1090/stml/009. ISBN 978-0-8218-2636-2. S2CID 118752074.
↑ Richard M. Timoney (2004), Riemann mapping theorem from Trinity College Dublin
↑ Geometry/Unified Angles at Wikibooks
↑ Tsurusaburo Takasu (1941) Gemeinsame Behandlungsweise der elliptischen konformen, hyperbolischen konformen und parabolischen konformen Differentialgeometrie, 2, Proceedings of the Imperial Academy 17(8): 330–8, link from Project Euclid, MR14282
↑ Selig, Michael S.; Maughmer, Mark D. (1992-05-01). "कंफर्मल मैपिंग पर आधारित मल्टीपॉइंट व्युत्क्रम एयरफ़ॉइल डिज़ाइन विधि". AIAA Journal. 30 (5): 1162–1170. Bibcode:1992AIAAJ..30.1162S. doi:10.2514/3.11046. ISSN 0001-1452.
↑ Cortijo, Vanessa; Alonso, Elena R.; Mata, Santiago; Alonso, José L. (2018-01-18). "फेनोलिक एसिड का गठन संबंधी मानचित्र". The Journal of Physical Chemistry A. 122 (2): 646–651. Bibcode:2018JPCA..122..646C. doi:10.1021/acs.jpca.7b08882. ISSN 1520-5215. PMID 29215883.
↑ "अनुरूप मानचित्रण के गुण".
↑ "7.1 GENETIC MAPS COME IN VARIOUS FORMS". www.informatics.jax.org. Retrieved 2022-08-22.
↑ Alim, Karen; Armon, Shahaf; Shraiman, Boris I.; Boudaoud, Arezki (2016). "पत्ती की वृद्धि अनुरूप होती है". Physical Biology. 13 (5): 05LT01. arXiv:1611.07032. Bibcode:2016PhBio..13eLT01A. doi:10.1088/1478-3975/13/5/05lt01. PMID 27597439. S2CID 9351765. Retrieved 2022-08-22.
↑ González-Matesanz, F. J.; Malpica, J. A. (2006-11-01). "परिवर्तनों के समन्वय के लिए आनुवंशिक एल्गोरिदम के साथ अर्ध-अनुरूप मानचित्रण लागू किया गया". Computers & Geosciences. 32 (9): 1432–1441. Bibcode:2006CG.....32.1432G. doi:10.1016/j.cageo.2006.01.002. ISSN 0098-3004.
↑ Berezovski, Volodymyr; Cherevko, Yevhen; Rýparová, Lenka (August 2019). "कुछ विशेष स्थानों पर अनुरूप और जियोडेसिक मैपिंग". Mathematics. 7 (8): 664. doi:10.3390/math7080664. ISSN 2227-7390.
↑ Gronwall, T. H. (June 1920). "वास्तविक कॉनिक्स के एक परिवार का दूसरे पर अनुरूप मानचित्रण". Proceedings of the National Academy of Sciences. 6 (6): 312–315. Bibcode:1920PNAS....6..312G. doi:10.1073/pnas.6.6.312. ISSN 0027-8424. PMC 1084530. PMID 16576504.
↑ "एक वाक्य में मानचित्रण (विशेषकर उद्धरण, कहावत जैसे अच्छे वाक्य...)". sentencedict.com. Retrieved 2022-08-22.
↑ "EAP - Proceedings of the Estonian Academy of Sciences – Publications". Retrieved 2022-08-22.
↑ López-Vázquez, Carlos (2012-01-01). "अनुभवजन्य विश्लेषणात्मक कार्यों का उपयोग करके स्थितिगत सटीकता में सुधार". Cartography and Geographic Information Science. 39 (3): 133–139. doi:10.1559/15230406393133. ISSN 1523-0406. S2CID 123894885.
↑ Calixto, Wesley Pacheco; Alvarenga, Bernardo; da Mota, Jesus Carlos; Brito, Leonardo da Cunha; Wu, Marcel; Alves, Aylton José; Neto, Luciano Martins; Antunes, Carlos F. R. Lemos (2011-02-15). "Electromagnetic Problems Solving by Conformal Mapping: A Mathematical Operator for Optimization". Mathematical Problems in Engineering. 2010: e742039. doi:10.1155/2010/742039. ISSN 1024-123X.
↑ Leonhardt, Ulf (2006-06-23). "ऑप्टिकल कंफर्मल मैपिंग". Science. 312 (5781): 1777–1780. Bibcode:2006Sci...312.1777L. doi:10.1126/science.1126493. ISSN 0036-8075. PMID 16728596. S2CID 8334444.
↑ Singh, Arun K.; Auton, Gregory; Hill, Ernie; Song, Aimin (2018-07-01). "कंफर्मल मैपिंग तकनीक का उपयोग करके ग्राफीन सेल्फ-स्विचिंग डायोड की आंतरिक और बाहरी कैपेसिटेंस का अनुमान". 2D Materials. 5 (3): 035023. Bibcode:2018TDM.....5c5023S. doi:10.1088/2053-1583/aac133. ISSN 2053-1583. S2CID 117531045.
↑ Kolaei, Amir; Rakheja, Subhash; Richard, Marc J. (2014-01-06). "टैंक वाहनों के क्षणिक पार्श्व स्लोश और रोल स्थिरता की भविष्यवाणी के लिए रैखिक द्रव स्लोश सिद्धांत की प्रयोज्यता की सीमा". Journal of Sound and Vibration. 333 (1): 263–282. Bibcode:2014JSV...333..263K. doi:10.1016/j.jsv.2013.09.002.
↑ Hinton, Edward; Hogg, Andrew; Huppert, Herbert (2020). "उथली मुक्त-सतह स्टोक्स एक कोने के चारों ओर बहती है". Philosophical Transactions of the Royal Society A. 378 (2174). Bibcode:2020RSPTA.37890515H. doi:10.1098/rsta.2019.0515. PMC 7287310. PMID 32507085.
↑ Noury, Keyvan; Yang, Bingen (2020). "A Pseudo S-plane Mapping of Z-plane Root Locus". ASME 2020 International Mechanical Engineering Congress and Exposition. American Society of Mechanical Engineers. doi:10.1115/IMECE2020-23096. ISBN 978-0-7918-8454-6. S2CID 234582511.
↑ Warwick, Andrew (2003). Masters of theory : Cambridge and the rise of mathematical physics. University of Chicago Press. pp. 404–424. ISBN 978-0226873756.

अग्रिम पठन

Ahlfors, Lars V. (1973), Conformal invariants: topics in geometric function theory, New York: McGraw–Hill Book Co., MR 0357743
Constantin Carathéodory (1932) Conformal Representation, Cambridge Tracts in Mathematics and Physics
Chanson, H. (2009), Applied Hydrodynamics: An Introduction to Ideal and Real Fluid Flows, CRC Press, Taylor & Francis Group, Leiden, The Netherlands, 478 pages, ISBN 978-0-415-49271-3
Churchill, Ruel V. (1974), Complex Variables and Applications, New York: McGraw–Hill Book Co., ISBN 978-0-07-010855-4
E.P. Dolzhenko (2001) [1994], "Conformal mapping", Encyclopedia of Mathematics, EMS Press
Rudin, Walter (1987), Real and complex analysis (3rd ed.), New York: McGraw–Hill Book Co., ISBN 978-0-07-054234-1, MR 0924157
Weisstein, Eric W. "Conformal Mapping". MathWorld.

बाहरी संबंध

Interactive visualizations of many conformal maps
Conformal Maps by Michael Trott, Wolfram Demonstrations Project.
Conformal Mapping images of current flow in different geometries without and with magnetic field by Gerhard Brunthaler.
Conformal Transformation: from Circle to Square.
Online Conformal Map Grapher.
Joukowski Transform Interactive WebApp

[1] Blair, David (2000-08-17). उलटा सिद्धांत और अनुरूप मानचित्रण. The Student Mathematical Library. Vol. 9. Providence, Rhode Island: American Mathematical Society. doi:10.1090/stml/009. ISBN 978-0-8218-2636-2. S2CID 118752074.

[2] Richard M. Timoney (2004), Riemann mapping theorem from Trinity College Dublin

[3] Geometry/Unified Angles at Wikibooks

[4] Tsurusaburo Takasu (1941) Gemeinsame Behandlungsweise der elliptischen konformen, hyperbolischen konformen und parabolischen konformen Differentialgeometrie, 2, Proceedings of the Imperial Academy 17(8): 330–8, link from Project Euclid, MR14282

[5] Selig, Michael S.; Maughmer, Mark D. (1992-05-01). "कंफर्मल मैपिंग पर आधारित मल्टीपॉइंट व्युत्क्रम एयरफ़ॉइल डिज़ाइन विधि". AIAA Journal. 30 (5): 1162–1170. Bibcode:1992AIAAJ..30.1162S. doi:10.2514/3.11046. ISSN 0001-1452.

[6] Cortijo, Vanessa; Alonso, Elena R.; Mata, Santiago; Alonso, José L. (2018-01-18). "फेनोलिक एसिड का गठन संबंधी मानचित्र". The Journal of Physical Chemistry A. 122 (2): 646–651. Bibcode:2018JPCA..122..646C. doi:10.1021/acs.jpca.7b08882. ISSN 1520-5215. PMID 29215883.

[7] "अनुरूप मानचित्रण के गुण".

[8] "7.1 GENETIC MAPS COME IN VARIOUS FORMS". www.informatics.jax.org. Retrieved 2022-08-22.

[9] Alim, Karen; Armon, Shahaf; Shraiman, Boris I.; Boudaoud, Arezki (2016). "पत्ती की वृद्धि अनुरूप होती है". Physical Biology. 13 (5): 05LT01. arXiv:1611.07032. Bibcode:2016PhBio..13eLT01A. doi:10.1088/1478-3975/13/5/05lt01. PMID 27597439. S2CID 9351765. Retrieved 2022-08-22.

[10] González-Matesanz, F. J.; Malpica, J. A. (2006-11-01). "परिवर्तनों के समन्वय के लिए आनुवंशिक एल्गोरिदम के साथ अर्ध-अनुरूप मानचित्रण लागू किया गया". Computers & Geosciences. 32 (9): 1432–1441. Bibcode:2006CG.....32.1432G. doi:10.1016/j.cageo.2006.01.002. ISSN 0098-3004.

[11] Berezovski, Volodymyr; Cherevko, Yevhen; Rýparová, Lenka (August 2019). "कुछ विशेष स्थानों पर अनुरूप और जियोडेसिक मैपिंग". Mathematics. 7 (8): 664. doi:10.3390/math7080664. ISSN 2227-7390.

[12] Gronwall, T. H. (June 1920). "वास्तविक कॉनिक्स के एक परिवार का दूसरे पर अनुरूप मानचित्रण". Proceedings of the National Academy of Sciences. 6 (6): 312–315. Bibcode:1920PNAS....6..312G. doi:10.1073/pnas.6.6.312. ISSN 0027-8424. PMC 1084530. PMID 16576504.

[13] "एक वाक्य में मानचित्रण (विशेषकर उद्धरण, कहावत जैसे अच्छे वाक्य...)". sentencedict.com. Retrieved 2022-08-22.

[14] "EAP - Proceedings of the Estonian Academy of Sciences – Publications". Retrieved 2022-08-22.

[15] López-Vázquez, Carlos (2012-01-01). "अनुभवजन्य विश्लेषणात्मक कार्यों का उपयोग करके स्थितिगत सटीकता में सुधार". Cartography and Geographic Information Science. 39 (3): 133–139. doi:10.1559/15230406393133. ISSN 1523-0406. S2CID 123894885.

[16] Calixto, Wesley Pacheco; Alvarenga, Bernardo; da Mota, Jesus Carlos; Brito, Leonardo da Cunha; Wu, Marcel; Alves, Aylton José; Neto, Luciano Martins; Antunes, Carlos F. R. Lemos (2011-02-15). "Electromagnetic Problems Solving by Conformal Mapping: A Mathematical Operator for Optimization". Mathematical Problems in Engineering. 2010: e742039. doi:10.1155/2010/742039. ISSN 1024-123X.

[17] Leonhardt, Ulf (2006-06-23). "ऑप्टिकल कंफर्मल मैपिंग". Science. 312 (5781): 1777–1780. Bibcode:2006Sci...312.1777L. doi:10.1126/science.1126493. ISSN 0036-8075. PMID 16728596. S2CID 8334444.

[18] Singh, Arun K.; Auton, Gregory; Hill, Ernie; Song, Aimin (2018-07-01). "कंफर्मल मैपिंग तकनीक का उपयोग करके ग्राफीन सेल्फ-स्विचिंग डायोड की आंतरिक और बाहरी कैपेसिटेंस का अनुमान". 2D Materials. 5 (3): 035023. Bibcode:2018TDM.....5c5023S. doi:10.1088/2053-1583/aac133. ISSN 2053-1583. S2CID 117531045.

[19] Kolaei, Amir; Rakheja, Subhash; Richard, Marc J. (2014-01-06). "टैंक वाहनों के क्षणिक पार्श्व स्लोश और रोल स्थिरता की भविष्यवाणी के लिए रैखिक द्रव स्लोश सिद्धांत की प्रयोज्यता की सीमा". Journal of Sound and Vibration. 333 (1): 263–282. Bibcode:2014JSV...333..263K. doi:10.1016/j.jsv.2013.09.002.

[20] Hinton, Edward; Hogg, Andrew; Huppert, Herbert (2020). "उथली मुक्त-सतह स्टोक्स एक कोने के चारों ओर बहती है". Philosophical Transactions of the Royal Society A. 378 (2174). Bibcode:2020RSPTA.37890515H. doi:10.1098/rsta.2019.0515. PMC 7287310. PMID 32507085.

[21] Noury, Keyvan; Yang, Bingen (2020). "A Pseudo S-plane Mapping of Z-plane Root Locus". ASME 2020 International Mechanical Engineering Congress and Exposition. American Society of Mechanical Engineers. doi:10.1115/IMECE2020-23096. ISBN 978-0-7918-8454-6. S2CID 234582511.

[22] Warwick, Andrew (2003). Masters of theory : Cambridge and the rise of mathematical physics. University of Chicago Press. pp. 404–424. ISBN 978-0226873756.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]