अर्ध-विभेदीकरण

गणना में, गणित की शाखा, वास्तविक चर के वास्तविक संख्या-मूल्य वाले फलन (गणित) f की एकपक्षीय भिन्नता और अर्ध-भिन्नता की धारणाएं भिन्नता से कमजोर होती हैं। विशेष रूप से, फलन f को बिंदु a पर सही अवकलनीय कहा जाता है, यदि, मोटे तौर पर कहा जा सकता है, तब व्युत्पन्न (गणित) को परिभाषित किया जा सकता है, जिससे कि फलन के तर्क x दाईं ओर से a की ओर जाता है, और बाएं ओर a पर भिन्न किया जा सकता है यदि व्युत्पन्न को x के रूप में परिभाषित किया जा सकता है जो बाएं ओर से a की ओर बढ़ता है।

एकल-आयामी स्थिति

इस फलन का चिह्नित बिंदु पर कोई व्युत्पन्न नहीं है, जिससे कि फलन वहां निरंतर फलन नहीं है। हालाँकि, इसमें सभी बिंदुओं पर सही व्युत्पन्न है

\partial _{+}f(a)

लगातार 0 के सामान्तर.

गणित में, बायां व्युत्पन्न और दायां व्युत्पन्न विशेष प्रकार का व्युत्पन्न (किसी फलन के परिवर्तन की दर) होता हैं जो किसी फलन के तर्क द्वारा केवल दिशा (बाएं या दाएं, अर्थात् कम या उच्च मान) में आंदोलन के लिए परिभाषित होते हैं।

परिभाषाएँ

मान लीजिए f वास्तविक संख्याओं के उपसमुच्चय I पर परिभाषित वास्तविक-मूल्यवान फलन को दर्शाता है।

यदि $a \in I$ , $I \cap$ $[a,\infty)$ का सीमा बिंदु होता है और एकपक्षीय सीमा होती है।

\partial _{+}f(a):=\lim _{\scriptstyle x\to a^{+} \atop \scriptstyle x\in I}{\frac {f(x)-f(a)}{x-a}}

वास्तविक संख्या के रूप में उपस्तिथ होती है, तब f को a पर 'सही अवकलनीय' कहा जाता है और सीमा ∂₊f(a) को a पर f का 'सही अवकलज' कहा जाता है।

यदि $a \in I$ , $I \cap$ $(-\infty, a]$ की सीमा बिंदु होती है और एकपक्षीय सीमा होती है।

\partial _{-}f(a):=\lim _{\scriptstyle x\to a^{-} \atop \scriptstyle x\in I}{\frac {f(x)-f(a)}{x-a}}

वास्तविक संख्या के रूप में उपस्तिथ है, तब f को a पर 'बायां अवकलनीय' कहा जाता है और सीमा ∂_–f(a) को a पर f का 'बायां अवकलज' कहा जाता है।

यदि $a \in I$ , $I \cap$ $[a,\infty)$ की सीमा बिंदु होती है और यदि f, a पर बाएँ और दाएँ अवकलनीय होता है, तब f को a पर 'अर्ध-विभेदनीय' कहा जाता है।

यदि बाएँ और दाएँ व्युत्पन्न समान होते हैं, तब उनका मान सामान्य (द्विदिशात्मक) व्युत्पन्न के समान होते है। इस प्रकार कोई सममित व्युत्पन्न को भी परिभाषित कर सकता है, जो बाएं और दाएं व्युत्पन्न (जब वह दोनों उपस्तिथ होते हैं) के अंकगणितीय माध्य के सामान्तर होता है, अतः सममित व्युत्पन्न तब उपस्तिथ हो सकता है जब सामान्य व्युत्पन्न उपस्तिथ नहीं होता है।^[1]

टिप्पणियाँ और उदाहरण

फलन अपने कार्यक्षेत्र के आंतरिक बिंदु a पर भिन्न होता है और यदि यह a पर अर्ध-विभेदित होता है और बायां व्युत्पन्न दाएं व्युत्पन्न के सामान्तर होता है।
अर्ध-विभेदनीय फलन का उदाहरण, जो अवकलनीय नहीं होता है, अतः $f(x)=|x|$ , a = 0 पर निरपेक्ष मान फलन है। इस प्रकार हम सरलता से $\partial _{-}f(0)=-1,\partial _{+}f(0)=1.$ प्राप्त करते हैं।
यदि कोई फलन किसी बिंदु a पर अर्ध-विभेदनीय होता है, तब इसका तात्पर्य यह होता है कि यह a पर निरंतर है।
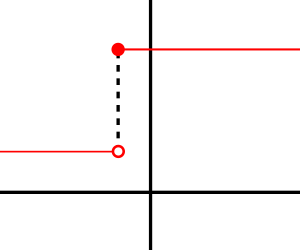
सूचक फलन 1_[0,∞) प्रत्येक वास्तविक a पर सही अवकलनीय होता है, किन्तु शून्य पर असंतत है (ध्यान दीजिए कि यह सूचक फलन शून्य पर अवकलनीय नहीं होता है)।

आवेदन

यदि वास्तविक रेखा के अंतराल I पर परिभाषित वास्तविक-मूल्यवान, अवकलनीय फलन f का प्रत्येक स्थान शून्य व्युत्पन्न होता है, तब यह स्थिर होता है, जैसा कि माध्य मान प्रमेय के अनुप्रयोग से पता चलता है। इस प्रकार भिन्नता की धारणा को f की निरंतरता और एकपक्षीय भिन्नता के कारण अशक्त किया जा सकता है। सामान्यतः दाएँ अवकलनीय कार्यों का संस्करण नीचे दिया गया है, अतः बाएँ अवकलनीय कार्यों का संस्करण अनुरूप होता है।

Theorem — मान लीजिए f वास्तविक-मूल्यवान है, सतत कार्य, अनैतिक रूप से परिभाषित मध्यान्तर I की वास्तविक रेखा होती है। यदि f प्रत्येक बिंदु पर सही अवकलनीय होता है $a \in I$ , जो अंतराल का सर्वोच्च नहीं होता है, और यदि यह सही व्युत्पन्न सदैव शून्य होता है, तब f स्थिर होता है।

Proof

For a proof by contradiction, assume there exist $a < b$ in I such that $f (a) \neq f (b)$ . Then

\varepsilon :={\frac {|f(b)-f(a)|}{2(b-a)}}>0.

Define c as the infimum of all those x in the interval $(a, b]$ for which the difference quotient of f exceeds ε in absolute value, i.e.

c=\inf\{\,x\in (a,b]\mid |f(x)-f(a)|>\varepsilon (x-a)\,\}.

Due to the continuity of f, it follows that $c < b$ and $| f (c) - f (a) | = ε (c - a)$ . At c the right derivative of f is zero by assumption, hence there exists d in the interval $(c, b]$ with $| f (x) - f (c) | \leq ε (x - c)$ for all x in $(c, d]$ . Hence, by the triangle inequality,

|f(x)-f(a)|\leq |f(x)-f(c)|+|f(c)-f(a)|\leq \varepsilon (x-a)

for all x in $[c, d)$ , which contradicts the definition of c.

बायीं या दायीं ओर कार्य करने वाले विभेदक ऑपरेटर

अन्य सामान्य उपयोग इन्फिक्स संकेतन में बाइनरी ऑपरेटरों के रूप में व्यवहार किए गए व्युत्पन्न का वर्णन करना है, जिसमें व्युत्पन्न को बाएं या दाएं ओपेरंड पर क्रियान्वित किया जाना है। इस प्रकार यह उपयोगी होता है, उदाहरण के लिए, पॉइसन ब्रैकेट के सामान्यीकरण को परिभाषित करते समय। फलन f और g की जोड़ी के लिए, बाएँ और दाएँ व्युत्पन्न को क्रमशः इस प्रकार परिभाषित किया गया है।

f{\stackrel {\leftarrow }{\partial }}_{x}g={\frac {\partial f}{\partial x}}\cdot g

f{\stackrel {\rightarrow }{\partial }}_{x}g=f\cdot {\frac {\partial g}{\partial x}}.

सामान्यतः ब्रा-केट संकेत चिन्ह में, व्युत्पन्न ऑपरेटर दाएं ऑपरेंड पर नियमित व्युत्पन्न के रूप में या बाईं ओर ऋणात्मक व्युत्पन्न के रूप में कार्य कर सकता है।^[2]

उच्च-आयामी स्थिति

इस उपरोक्त परिभाषा को दिशात्मक व्युत्पन्न के कमजोर संस्करण का उपयोग करके 'Rⁿ' के उपसमुच्चय पर परिभाषित वास्तविक-मूल्यवान कार्यों के लिए सामान्यीकृत किया जा सकता है। मान लीजिए a, f के प्रांत का आंतरिक बिंदु होता है। इस प्रकार तब बिंदु a पर f को अर्ध-विभेदक कहा जाता है यदि प्रत्येक दिशा के लिए u ∈ 'Rⁿ' सीमा होती है।

\partial _{u}f(a)=\lim _{h\to 0^{+}}{\frac {f(a+h\,u)-f(a)}{h}}

साथ ही $h\in$ R वास्तविक संख्या के रूप में उपस्तिथ होता है।

इस प्रकार अर्ध-विभेदीकरण गेटॉक्स व्युत्पन्न की तुलना में कमजोर होता है, जिसके लिए कोई h को केवल धनात्मक मानों तक सीमित किए बिना h → 0 से ऊपर की सीमा लेता है।

उदाहरण के लिए, फलन $f(x,y)={\sqrt {x^{2}+y^{2}}}$ पर अर्ध-विभेद्य होता है $(0,0)$ , किन्तु गेटॉक्स वहां भिन्न नहीं होता है। वास्तव में,

 $f(hx,hy)=|h|f(x,y){\text{ and for }}h\geq 0,f(hx,hy)=hf(x,y),f(hx,hy)/h=f(x,y),$  साथ  $a=0,u=(x,y),\partial _{u}f(0)=f(x,y)$

(ध्यान दीजिए कि यह सामान्यीकरण n = 1 की मूल परिभाषा के सामान्तर नहीं है जिससे कि एकपक्षीय सीमा बिंदुओं की अवधारणा को आंतरिक बिंदुओं की मजबूत अवधारणा से परिवर्तित कर दिया गया है।)

गुण

Rⁿ के उत्तल खुले उपसमुच्चय पर कोई भी उत्तल फलन अर्ध-विभेदनीय होता है।
जबकि चर का प्रत्येक अर्ध-विभेद्य फलन सतत होता है। इस प्रकार यह अब अनेक चरों के लिए सत्य नहीं होता है।

सामान्यीकरण

वास्तविक-मूल्यवान फलन के अतिरिक्त, कोई Rⁿ या बनच स्थान में मान लेने वाले फलन पर विचार कर सकता है।

यह भी देखें

व्युत्पन्न
दिशात्मक व्युत्पन्न
आंशिक व्युत्पन्न
ढाल
गैटेक्स व्युत्पन्न
फ़्रेचेट व्युत्पन्न
व्युत्पन्न (सामान्यीकरण)
चरण अंतरिक्ष सूत्रीकरण#स्टार उत्पाद
दीनी व्युत्पन्न

संदर्भ

↑ Peter R. Mercer (2014). एकल चर का अधिक कैलकुलस. Springer. p. 173. ISBN 978-1-4939-1926-0.
↑ Dirac, Paul (1982) [1930]. क्वांटम यांत्रिकी के सिद्धांत. USA: Oxford University Press. ISBN 978-0198520115.

Preda, V.; Chiţescu, I. (1999). "On Constraint Qualification in Multiobjective Optimization Problems: Semidifferentiable Case". J. Optim. Theory Appl. 100 (2): 417–433. doi:10.1023/A:1021794505701. S2CID 119868047.

[Mercer2014-1] Peter R. Mercer (2014). एकल चर का अधिक कैलकुलस. Springer. p. 173. ISBN 978-1-4939-1926-0.

[2] Dirac, Paul (1982) [1930]. क्वांटम यांत्रिकी के सिद्धांत. USA: Oxford University Press. ISBN 978-0198520115.

[1]

[2]