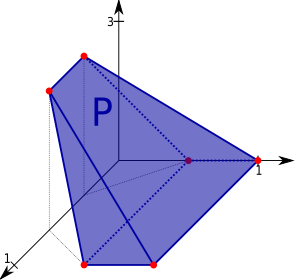
उत्तल पॉलीटोप

एक 3-आयामी उत्तल पॉलीटोप

एक उत्तल बहुवचन एक पॉलीटोप का एक विशेष मामला है, जिसमें अतिरिक्त संपत्ति है कि यह एक उत्तल सेट भी है जो इसमें निहित है $n$ -आयामी यूक्लिडियन अंतरिक्ष $\mathbb {R} ^{n}$ . अधिकांश ग्रंथ^[1]^[2] एक परिबद्ध सेट उत्तल पॉलीटोप के लिए पॉलीटोप शब्द का उपयोग करें, और अधिक सामान्य, संभवतः असंबद्ध वस्तु के लिए पॉलीहेड्रॉन शब्द का उपयोग करें। अन्य^[3] (इस लेख सहित) पॉलीटोप्स को असीमित होने की अनुमति देता है। जब भी चर्चा किए गए मुद्दे के लिए सीमा महत्वपूर्ण होगी, तो परिबद्ध/अनबाउंड उत्तल पॉलीटोप शब्दों का उपयोग नीचे किया जाएगा। फिर भी अन्य पाठ इसकी सीमा के साथ एक उत्तल बहुविषय की पहचान करते हैं।

उत्तल पॉलीटोप्स गणित की विभिन्न शाखाओं और व्यावहारिक क्षेत्रों दोनों में महत्वपूर्ण भूमिका निभाते हैं, विशेष रूप से रैखिक प्रोग्रामिंग में।

ग्रुनबाम की प्रभावशाली पाठ्यपुस्तकों में^[1]और ज़िग्लर^[2]विषय पर, साथ ही असतत ज्यामिति के कई अन्य ग्रंथों में, उत्तल पॉलीटोप्स को अक्सर पॉलीटोप्स कहा जाता है। ग्रुनबाम बताते हैं कि यह पूरी तरह से उत्तल शब्द की अंतहीन पुनरावृत्ति से बचने के लिए है, और यह कि चर्चा को केवल उत्तल विविधता (पृष्ठ 51) पर लागू करने के रूप में समझा जाना चाहिए।

एक पॉलीटोप को पूर्ण-आयामी कहा जाता है यदि यह एक है $n$ -आयामी वस्तु में $\mathbb {R} ^{n}$ .

उदाहरण

बाउंडेड उत्तल पॉलीटोप्स के कई उदाहरण बहुतल लेख में पाए जा सकते हैं।
द्वि-आयामी मामले में पूर्ण-आयामी उदाहरण एक अर्ध-तल, दो समानांतर रेखाओं के बीच एक पट्टी, एक कोण आकार (दो गैर-समानांतर अर्ध-तलों का प्रतिच्छेदन), एक उत्तल बहुभुज श्रृंखला द्वारा परिभाषित आकृति है। इसके सिरों से जुड़ी दो किरणें (ज्यामिति) और एक उत्तल बहुभुज।
अनबाउंड उत्तल पॉलीटोप के विशेष मामले दो समानांतर हाइपरप्लेन के बीच एक स्लैब (ज्यामिति), दो गैर-समानांतर अर्ध-स्थान (ज्यामिति) | अर्ध-स्थान, एक बहुफलकीय सिलेंडर (अनंत प्रिज्म (ज्यामिति)) द्वारा परिभाषित एक पच्चर, और हैं। एक बहुफलकीय शंकु (अनंत शंकु) जो एक सामान्य बिंदु से गुजरने वाले तीन या अधिक अर्ध-स्थानों द्वारा परिभाषित होता है।

परिभाषाएँ

उत्तल पॉलीटोप को कई तरीकों से परिभाषित किया जा सकता है, जो इस बात पर निर्भर करता है कि मौजूदा समस्या के लिए क्या अधिक उपयुक्त है। ग्रुनबाम की परिभाषा अंतरिक्ष में बिंदुओं के उत्तल सेट के संदर्भ में है। अन्य महत्वपूर्ण परिभाषाएँ हैं: अर्ध-स्थान (ज्यामिति) के प्रतिच्छेदन (सेट सिद्धांत) के रूप में | अर्ध-स्थान (आधा-स्थान प्रतिनिधित्व) और बिंदुओं के एक सेट (शीर्ष प्रतिनिधित्व) के उत्तल पतवार के रूप में।

शीर्ष प्रतिनिधित्व (उत्तल पतवार)

अपनी पुस्तक उत्तल पॉलीटोप्स में, ग्रुनबाम ने उत्तल पॉलीटोप को 'एक सीमित संख्या में चरम बिंदुओं के साथ सघन स्थान उत्तल सेट' के रूप में परिभाषित किया है:

एक सेट

K

का

\mathbb {R} ^{n}

यदि प्रत्येक जोड़ी अलग-अलग बिंदुओं के लिए उत्तल है

a

,

b

में

K

, समापन बिंदुओं वाला बंद खंड

a

और

b

भीतर समाहित है

K

.

यह एक परिमित उत्तल पॉलीटोप को बिंदुओं के एक सीमित सेट के उत्तल पतवार के रूप में परिभाषित करने के बराबर है, जहां परिमित सेट में पॉलीटोप के चरम बिंदुओं का सेट होना चाहिए। ऐसी परिभाषा को शीर्ष प्रतिनिधित्व (वी-प्रतिनिधित्व या वी-विवरण) कहा जाता है।^[1] एक कॉम्पैक्ट उत्तल पॉलीटोप के लिए, न्यूनतम वी-विवरण अद्वितीय है और यह पॉलीटोप के शीर्ष (ज्यामिति) के सेट द्वारा दिया गया है।^[1]एक उत्तल पॉलीटोप को इंटीग्रल पॉलीटोप कहा जाता है यदि इसके सभी शीर्षों में पूर्णांक निर्देशांक हों।

आधे स्थानों का प्रतिच्छेदन

एक उत्तल पॉलीटोप को सीमित संख्या में आधे-स्थानों के प्रतिच्छेदन के रूप में परिभाषित किया जा सकता है। ऐसी परिभाषा को अर्ध-अंतरिक्ष प्रतिनिधित्व (एच-प्रतिनिधित्व या एच-विवरण) कहा जाता है।^[1] उत्तल पॉलीटोप के अनंत रूप से कई एच-विवरण मौजूद हैं। हालाँकि, एक पूर्ण-आयामी उत्तल पॉलीटोप के लिए, न्यूनतम एच-विवरण वास्तव में अद्वितीय है और पहलू (ज्यामिति)-परिभाषित आधे स्थानों के सेट द्वारा दिया गया है।^[1]

एक बंद आधे स्थान को एक रैखिक असमानता के रूप में लिखा जा सकता है:^[1]

a_{1}x_{1}+a_{2}x_{2}+\cdots +a_{n}x_{n}\leq b

कहाँ $n$ विचाराधीन पॉलीटोप वाले स्थान का आयाम है। इसलिए, एक बंद उत्तल पॉलीटोप को रैखिक असमानताओं की प्रणाली के समाधान के सेट के रूप में माना जा सकता है:

{\begin{alignedat}{7}a_{11}x_{1}&&\;+\;&&a_{12}x_{2}&&\;+\cdots +\;&&a_{1n}x_{n}&&\;\leq \;&&&b_{1}\\a_{21}x_{1}&&\;+\;&&a_{22}x_{2}&&\;+\cdots +\;&&a_{2n}x_{n}&&\;\leq \;&&&b_{2}\\\vdots \;\;\;&&&&\vdots \;\;\;&&&&\vdots \;\;\;&&&&&\;\vdots \\a_{m1}x_{1}&&\;+\;&&a_{m2}x_{2}&&\;+\cdots +\;&&a_{mn}x_{n}&&\;\leq \;&&&b_{m}\\\end{alignedat}}

कहाँ $m$ पॉलीटोप को परिभाषित करने वाले आधे-रिक्त स्थानों की संख्या है। इसे संक्षेप में मैट्रिक्स (गणित) असमानता के रूप में लिखा जा सकता है:

Ax\leq b

कहाँ $A$ एक $m\times n$ आव्यूह, $x$ एक $n\times 1$ स्तंभ वेक्टर जिसके निर्देशांक चर हैं $x_{1}$ को $x_{n}$ , और $b$ एक $m\times 1$ स्तंभ वेक्टर जिसके निर्देशांक दाहिनी ओर हैं $b_{1}$ को $b_{m}$ अदिश असमानताओं का.

एक खुले उत्तल पॉलीटोप को उसी तरह परिभाषित किया गया है, जिसमें गैर-सख्त असमानताओं के बजाय सूत्रों में सख्त असमानताओं का उपयोग किया गया है।

की प्रत्येक पंक्ति के गुणांक $A$ और $b$ संबंधित अर्ध-स्थान को परिभाषित करने वाली रैखिक असमानता के गुणांक के अनुरूप। इसलिए, मैट्रिक्स में प्रत्येक पंक्ति पॉलीटोप के एक सहायक हाइपरप्लेन से मेल खाती है, एक हाइपरप्लेन जो आधे स्थान को घेरता है जिसमें पॉलीटोप होता है। यदि एक सहायक हाइपरप्लेन भी पॉलीटोप को काटता है, तो इसे बाउंडिंग हाइपरप्लेन कहा जाता है (चूँकि यह एक सहायक हाइपरप्लेन है, यह केवल पॉलीटोप की सीमा पर पॉलीटोप को काट सकता है)।

उपरोक्त परिभाषा मानती है कि पॉलीटोप पूर्ण-आयामी है। इस मामले में, असमानताओं को परिभाषित करने का एक अद्वितीय न्यूनतम सेट है (एक सकारात्मक संख्या से गुणा तक)। इस अद्वितीय न्यूनतम प्रणाली से संबंधित असमानताओं को आवश्यक कहा जाता है। एक पॉलीटोप के बिंदुओं का समूह जो समानता के साथ एक आवश्यक असमानता को संतुष्ट करता है, एक पहलू कहलाता है।

यदि पॉलीटोप पूर्ण-आयामी नहीं है, तो इसका समाधान $Ax\leq b$ के उचित एफ़िन उपस्थान में स्थित है $\mathbb {R} ^{n}$ और इस उपस्थान में पॉलीटोप का एक वस्तु के रूप में अध्ययन किया जा सकता है। इस मामले में, ऐसे रैखिक समीकरण मौजूद हैं जो पॉलीटोप के सभी बिंदुओं से संतुष्ट होते हैं। इनमें से किसी एक समीकरण को किसी भी परिभाषित असमानता में जोड़ने से बहुविषयक परिवर्तन नहीं होता है। इसलिए, सामान्य तौर पर पॉलीटोप को परिभाषित करने वाली असमानताओं का कोई अद्वितीय न्यूनतम सेट नहीं है।

सामान्य तौर पर मनमाने आधे-स्थानों के प्रतिच्छेदन को सीमित करने की आवश्यकता नहीं है। हालाँकि, यदि कोई उत्तल पतवार के बराबर परिभाषा चाहता है, तो बाउंडिंग की स्पष्ट रूप से आवश्यकता होनी चाहिए।

विभिन्न अभ्यावेदन का उपयोग करना

दोनों निरूपण मिलकर यह तय करने का एक कुशल तरीका प्रदान करते हैं कि क्या दिया गया वेक्टर किसी दिए गए उत्तल पॉलीटोप में शामिल है: यह दिखाने के लिए कि यह पॉलीटोप में है, इसे पॉलीटोप शीर्षों के उत्तल संयोजन के रूप में प्रस्तुत करना पर्याप्त है (वी-विवरण प्रयोग किया जाता है); यह दिखाने के लिए कि यह बहुवचन में नहीं है, यह एक एकल परिभाषित असमानता प्रस्तुत करने के लिए पर्याप्त है जिसका यह उल्लंघन करता है।^[4]^: 256

सदिशों द्वारा निरूपण में एक सूक्ष्म बिंदु यह है कि आयाम में सदिशों की संख्या घातांकीय हो सकती है, इसलिए यह प्रमाण कि एक सदिश पॉलीटोप में है, घातांकीय रूप से लंबा हो सकता है। सौभाग्य से, कैराथोडोरी का प्रमेय (उत्तल पतवार) | कैराथोडोरी का प्रमेय गारंटी देता है कि पॉलीटोप में प्रत्येक वेक्टर को अधिकतम डी+1 परिभाषित वैक्टर द्वारा दर्शाया जा सकता है, जहां डी अंतरिक्ष का आयाम है।

अनबाउंड पॉलीटोप्स का प्रतिनिधित्व

एक असीमित पॉलीटोप (जिसे कभी-कभी पॉलीहेड्रॉन भी कहा जाता है) के लिए, एच-विवरण अभी भी मान्य है, लेकिन वी-विवरण को बढ़ाया जाना चाहिए। थिओडोर मोत्ज़किन (1936) ने साबित किया कि किसी भी असंबद्ध पॉलीटोप को एक बंधे हुए पॉलीटोप और उत्तल शंकु के योग के रूप में दर्शाया जा सकता है।^[5] दूसरे शब्दों में, एक असीमित पॉलीटोप में प्रत्येक वेक्टर इसके शीर्षों (इसके परिभाषित बिंदु) का एक उत्तल योग है, साथ ही इसके अनंत किनारों (इसकी परिभाषित किरणें) के यूक्लिडियन वेक्टर का एक शंक्वाकार योग है। इसे परिमित आधार प्रमेय कहा जाता है।^[3]

गुण

प्रत्येक (परिबद्ध) उत्तल पॉलीटोप एक संकेतन की छवि है, क्योंकि प्रत्येक बिंदु (अंततः कई) शीर्षों का उत्तल संयोजन है। हालाँकि, पॉलीटोप्स सामान्य रूप से सरलताओं के समरूपी नहीं होते हैं। यह वेक्टर रिक्त स्थान और रैखिक संयोजनों के मामले के विपरीत है, प्रत्येक परिमित-आयामी वेक्टर स्पेस न केवल एक छवि है, बल्कि वास्तव में कुछ आयाम (या अन्य क्षेत्रों के अनुरूप) के यूक्लिडियन स्पेस की आइसोमोर्फिक है।

चेहरा जाली

उत्तल पॉलीटोप का एक चेहरा (ज्यामिति) आधे-स्थान (ज्यामिति) के साथ पॉलीटोप का कोई भी चौराहा होता है, जैसे कि पॉलीटोप का कोई भी आंतरिक बिंदु आधे स्थान की सीमा पर नहीं होता है। समान रूप से, एक फलक पॉलीटोप की कुछ वैध असमानताओं में समानता देने वाले बिंदुओं का समूह है।^[4]^: 258

यदि एक पॉलीटोप डी-आयामी है, तो इसका पहलू (गणित) इसके (डी -1)-आयामी चेहरे हैं, इसका शीर्ष (ज्यामिति) इसके 0-आयामी चेहरे हैं, इसके किनारे (ज्यामिति) इसके 1-आयामी चेहरे हैं, और इसके रिज (ज्यामिति) इसके (डी − 2)-आयामी चेहरे हैं।

मैट्रिक्स असमानता द्वारा परिभाषित उत्तल पॉलीटोप पी दिया गया है $Ax\leq b$ , यदि A में प्रत्येक पंक्ति एक बाउंडिंग हाइपरप्लेन से मेल खाती है और अन्य पंक्तियों से रैखिक रूप से स्वतंत्र है, तो P का प्रत्येक पहलू A की बिल्कुल एक पंक्ति से मेल खाता है, और इसके विपरीत। किसी दिए गए पहलू पर प्रत्येक बिंदु मैट्रिक्स में संबंधित पंक्ति की रैखिक समानता को संतुष्ट करेगा। (यह अन्य पंक्तियों में समानता को संतुष्ट कर भी सकता है और नहीं भी)। इसी प्रकार, रिज पर प्रत्येक बिंदु ए की दो पंक्तियों में समानता को संतुष्ट करेगा।

एक वर्गाकार पिरामिड का मुख जाली, हस्से आरेख के रूप में खींचा गया; जाली में प्रत्येक फलक को उसके शीर्ष सेट द्वारा लेबल किया गया है।

सामान्य तौर पर, एक (एन - जे)-आयामी चेहरा ए की जे विशिष्ट पंक्तियों में समानता को संतुष्ट करता है। ये पंक्तियाँ चेहरे का 'आधार' बनाती हैं। ज्यामितीय रूप से बोलते हुए, इसका मतलब है कि चेहरा पॉलीटोप पर बिंदुओं का समूह है जो पॉलीटोप के बाउंडिंग हाइपरप्लेन के जे के चौराहे पर स्थित है।

उत्तल पॉलीटोप के फलक इस प्रकार एक यूलेरियन पोसेट जाली (ऑर्डर) बनाते हैं, जिसे इसका 'फेस लैटिस' कहा जाता है, जहां आंशिक क्रम चेहरों के निर्धारित नियंत्रण से होता है। ऊपर दी गई चेहरे की परिभाषा पॉलीटोप और खाली सेट दोनों को चेहरे के रूप में मानने की अनुमति देती है, जिससे यह सुनिश्चित होता है कि चेहरे की प्रत्येक जोड़ी में चेहरे की जाली में एक जोड़ और एक मिलन होता है। संपूर्ण पॉलीटोप जाली का अद्वितीय अधिकतम तत्व है, और खाली सेट, जिसे प्रत्येक पॉलीटोप का (−1)-आयामी चेहरा (एक 'शून्य पॉलीटोप') माना जाता है, जाली का अद्वितीय न्यूनतम तत्व है।

दो पॉलीटोप्स को 'कॉम्बिनेटोरियलली आइसोमोर्फिक' कहा जाता है यदि उनके चेहरे की जाली समाकृतिकता हैं।

'पॉलीटोप ग्राफ' ('पॉलीटोपल ग्राफ', 'पॉलीटोप का ग्राफ', '1-कंकाल') उच्च-आयामी चेहरों को नजरअंदाज करते हुए केवल पॉलीटोप के शीर्षों और किनारों का सेट है। उदाहरण के लिए, एक बहुफलकीय ग्राफ एक त्रि-आयामी पॉलीटोप का पॉलीटोप ग्राफ है। हस्लर व्हिटनी के परिणाम से^[6] त्रि-आयामी पॉलीटोप का चेहरा जाली उसके ग्राफ द्वारा निर्धारित किया जाता है। मनमाने आयाम के सरल बहुवचन के लिए भी यही सच है (ब्लाइंड एंड मणि-लेवित्स्का 1987, मीका मोती के अनुमान को साबित करते हुए)।^[7] कलाई (1988)^[8] अद्वितीय सिंक अभिविन्यासों के आधार पर एक सरल प्रमाण देता है। क्योंकि इन पॉलीटोप्स के फेस लैटिस उनके ग्राफ़ द्वारा निर्धारित किए जाते हैं, यह तय करने की समस्या कि क्या दो त्रि-आयामी या सरल उत्तल पॉलीटोप्स कॉम्बिनेटरियल रूप से आइसोमोर्फिक हैं, ग्राफ़ आइसोमोर्फिज्म समस्या के एक विशेष मामले के रूप में समकक्ष रूप से तैयार किया जा सकता है। हालाँकि, इन समस्याओं का विपरीत दिशा में अनुवाद करना भी संभव है, जिससे पता चलता है कि पॉलीटोप आइसोमोर्फिज्म परीक्षण ग्राफ समरूपता समस्या^[9]

टोपोलॉजिकल गुण

एक उत्तल पॉलीटोप, आर के किसी भी कॉम्पैक्ट उत्तल उपसमुच्चय की तरहⁿ, एक बंद गेंद (गणित) के लिए समरूपता है।^[10] मान लीजिए m पॉलीटोप के आयाम को दर्शाता है। यदि पॉलीटोप पूर्ण-आयामी है, तो m = n. उत्तल पॉलीटोप इसलिए सीमा के साथ एक एम-आयामी मैनिफोल्ड (गणित) है, इसकी यूलर विशेषता 1 है, और इसका मौलिक समूह तुच्छ है। उत्तल पॉलीटोप की सीमा n-गोले|(m − 1)-गोले के समरूप है। सीमा की यूलर विशेषता सम m के लिए 0 और विषम m के लिए 2 है। सीमा को (m − 1)-आयामी अण्डाकार स्थान के चौकोर के रूप में भी माना जा सकता है - यानी एक गोलाकार टाइलिंग के रूप में।

सरल अपघटन

एक उत्तल पॉलीटोप को कुछ गुणों को संतुष्ट करते हुए एक सरल परिसर, या सिंप्लेक्स के संघ में विघटित किया जा सकता है।

एक उत्तल आर-आयामी पॉलीटोप पी दिया गया है, इसके शीर्षों का एक उपसमुच्चय जिसमें (r+1) पूर्णतः स्वतंत्र बिंदु होते हैं, एक सिंप्लेक्स|r-सिंप्लेक्स को परिभाषित करता है। उपसमुच्चय का एक संग्रह बनाना संभव है जैसे कि संबंधित सरलताओं का मिलन P के बराबर हो, और किन्हीं दो सरलियों का प्रतिच्छेदन या तो खाली हो या निम्न-आयामी सरल हो। यह सरल अपघटन उत्तल पॉलीटोप की मात्रा की गणना के लिए कई तरीकों का आधार है, क्योंकि एक सिंप्लेक्स की मात्रा आसानी से एक सूत्र द्वारा दी जाती है।^[11]

उत्तल पॉलीटोप के लिए एल्गोरिदमिक समस्याएं

अभ्यावेदन का निर्माण

उत्तल पॉलीटोप के विभिन्न निरूपणों की अलग-अलग उपयोगिता होती है, इसलिए एक निरूपण को दूसरे निरूपण से निर्मित करना एक महत्वपूर्ण समस्या है। वी-प्रतिनिधित्व के निर्माण की समस्या को शीर्ष गणना समस्या के रूप में जाना जाता है और एच-प्रतिनिधित्व के निर्माण की समस्या को पहलू गणना समस्या के रूप में जाना जाता है। जबकि एक बंधे हुए उत्तल पॉलीटोप का शीर्ष सेट विशिष्ट रूप से इसे परिभाषित करता है, विभिन्न अनुप्रयोगों में पॉलीटोप की संयोजन संरचना के बारे में अधिक जानना महत्वपूर्ण है, अर्थात, इसके चेहरे की जाली के बारे में। विभिन्न उत्तल पतवार एल्गोरिदम पहलू गणना और चेहरा जाली निर्माण दोनों से निपटते हैं।

समतल मामले में, यानी, एक उत्तल बहुभुज के लिए, पहलू और शीर्ष दोनों की गणना की समस्याएं उत्तल पतवार के चारों ओर क्रमबद्ध शीर्षों (सम्मान किनारों) तक होती हैं। यह एक तुच्छ कार्य है जब उत्तल बहुभुज को बहुभुजों के लिए पारंपरिक तरीके से निर्दिष्ट किया जाता है, अर्थात, इसके शीर्षों के क्रमबद्ध अनुक्रम द्वारा $v_{1},\dots ,v_{m}$ . जब शीर्षों (या किनारों) की इनपुट सूची अव्यवस्थित होती है, तो समस्याओं की समय जटिलता बिग ओह संकेतन (एम लॉग एम) बन जाती है।^[12] गणना के बीजगणितीय निर्णय वृक्ष मॉडल में एक मिलान निचली सीमा ज्ञात होती है।^[13]

आयतन गणना

कम्प्यूटेशनल ज्यामिति के क्षेत्र में उत्तल पॉलीटोप की मात्रा की गणना करने के कार्य का अध्ययन किया गया है। वॉल्यूम की गणना सन्निकटन एल्गोरिदम से की जा सकती है, उदाहरण के लिए, सदस्यता ओरेकल मशीन तक पहुंच होने पर, उत्तल वॉल्यूम सन्निकटन तकनीक का उपयोग करके। सटीक एल्गोरिथ्म के लिए, एक बाधा यह है कि, जब रैखिक असमानता की समीकरण प्रणाली के रूप में उत्तल पॉलीटोप का प्रतिनिधित्व दिया जाता है, तो पॉलीटोप की मात्रा में बिट-लंबाई हो सकती है जो इस प्रतिनिधित्व में बहुपद नहीं है।^[14]

यह भी देखें

ओरिएंटेड मैट्रोइड
नेफ पॉलीहेड्रॉन
उत्तल पॉलीहेड्रा के लिए स्टीनित्ज़ का प्रमेय

संदर्भ

↑ ^1.0 ^1.1 ^1.2 ^1.3 ^1.4 ^1.5 ^1.6 Branko Grünbaum, Convex Polytopes, 2nd edition, prepared by Volker Kaibel, Victor Klee, and Günter M. Ziegler, 2003, ISBN 0-387-40409-0, ISBN 978-0-387-40409-7, 466pp.
↑ ^2.0 ^2.1 Ziegler, Günter M. (1995), Lectures on Polytopes, Graduate Texts in Mathematics, vol. 152, Berlin, New York: Springer-Verlag.
↑ ^3.0 ^3.1 Mathematical Programming, by Melvyn W. Jeter (1986) ISBN 0-8247-7478-7, p. 68
↑ ^4.0 ^4.1 Lovász, László; Plummer, M. D. (1986), Matching Theory, Annals of Discrete Mathematics, vol. 29, North-Holland, ISBN 0-444-87916-1, MR 0859549
↑ Motzkin, Theodore (1936). रैखिक असमानताओं के सिद्धांत में योगदान (पीएचडी शोध प्रबंध). Jerusalem.
↑ Whitney, Hassler (1932). "सर्वांगसम ग्राफ़ और ग्राफ़ की कनेक्टिविटी". Amer. J. Math. 54 (1): 150–168. doi:10.2307/2371086. hdl:10338.dmlcz/101067. JSTOR 2371086.
↑ Blind, Roswitha; Mani-Levitska, Peter (1987), "Puzzles and polytope isomorphisms", Aequationes Mathematicae, 34 (2–3): 287–297, doi:10.1007/BF01830678, MR 0921106.
↑ Kalai, Gil (1988), "A simple way to tell a simple polytope from its graph", Journal of Combinatorial Theory, Ser. A, 49 (2): 381–383, doi:10.1016/0097-3165(88)90064-7, MR 0964396.
↑ Kaibel, Volker; Schwartz, Alexander (2003). "पॉलीटोप समरूपता समस्याओं की जटिलता पर". Graphs and Combinatorics. 19 (2): 215–230. arXiv:math/0106093. doi:10.1007/s00373-002-0503-y. Archived from the original on 2015-07-21.
↑ Glen E. Bredon, Topology and Geometry, 1993, ISBN 0-387-97926-3, p. 56.
↑ Büeler, B.; Enge, A.; Fukuda, K. (2000). "Exact Volume Computation for Polytopes: A Practical Study". Polytopes — Combinatorics and Computation. p. 131. doi:10.1007/978-3-0348-8438-9_6. ISBN 978-3-7643-6351-2.
↑ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "33.3 Finding the convex hull". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 947–957. ISBN 0-262-03293-7.
↑ Yao, Andrew Chi Chih (1981), "A lower bound to finding convex hulls", Journal of the ACM, 28 (4): 780–787, doi:10.1145/322276.322289, MR 0677089; Ben-Or, Michael (1983), "Lower Bounds for Algebraic Computation Trees", Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing (STOC '83), pp. 80–86, doi:10.1145/800061.808735.
↑ Lawrence, Jim (1991). "पॉलीटोप वॉल्यूम गणना". Mathematics of Computation. 57 (195): 259–271. doi:10.1090/S0025-5718-1991-1079024-2. ISSN 0025-5718.

बाहरी संबंध

[grun-1] 1.0 ^1.1 ^1.2 ^1.3 ^1.4 ^1.5 ^1.6 Branko Grünbaum, Convex Polytopes, 2nd edition, prepared by Volker Kaibel, Victor Klee, and Günter M. Ziegler, 2003, ISBN 0-387-40409-0, ISBN 978-0-387-40409-7, 466pp.

[zieg-2] 2.0 ^2.1 Ziegler, Günter M. (1995), Lectures on Polytopes, Graduate Texts in Mathematics, vol. 152, Berlin, New York: Springer-Verlag.

[Jeter-3] 3.0 ^3.1 Mathematical Programming, by Melvyn W. Jeter (1986) ISBN 0-8247-7478-7, p. 68

[lp-4] 4.0 ^4.1 Lovász, László; Plummer, M. D. (1986), Matching Theory, Annals of Discrete Mathematics, vol. 29, North-Holland, ISBN 0-444-87916-1, MR 0859549

[5] Motzkin, Theodore (1936). रैखिक असमानताओं के सिद्धांत में योगदान (पीएचडी शोध प्रबंध). Jerusalem.

[6] Whitney, Hassler (1932). "सर्वांगसम ग्राफ़ और ग्राफ़ की कनेक्टिविटी". Amer. J. Math. 54 (1): 150–168. doi:10.2307/2371086. hdl:10338.dmlcz/101067. JSTOR 2371086.

[7] Blind, Roswitha; Mani-Levitska, Peter (1987), "Puzzles and polytope isomorphisms", Aequationes Mathematicae, 34 (2–3): 287–297, doi:10.1007/BF01830678, MR 0921106.

[8] Kalai, Gil (1988), "A simple way to tell a simple polytope from its graph", Journal of Combinatorial Theory, Ser. A, 49 (2): 381–383, doi:10.1016/0097-3165(88)90064-7, MR 0964396.

[9] Kaibel, Volker; Schwartz, Alexander (2003). "पॉलीटोप समरूपता समस्याओं की जटिलता पर". Graphs and Combinatorics. 19 (2): 215–230. arXiv:math/0106093. doi:10.1007/s00373-002-0503-y. Archived from the original on 2015-07-21.

[bredon-10] Glen E. Bredon, Topology and Geometry, 1993, ISBN 0-387-97926-3, p. 56.

[11] Büeler, B.; Enge, A.; Fukuda, K. (2000). "Exact Volume Computation for Polytopes: A Practical Study". Polytopes — Combinatorics and Computation. p. 131. doi:10.1007/978-3-0348-8438-9_6. ISBN 978-3-7643-6351-2.

[12] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "33.3 Finding the convex hull". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 947–957. ISBN 0-262-03293-7.

[13] Yao, Andrew Chi Chih (1981), "A lower bound to finding convex hulls", Journal of the ACM, 28 (4): 780–787, doi:10.1145/322276.322289, MR 0677089; Ben-Or, Michael (1983), "Lower Bounds for Algebraic Computation Trees", Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing (STOC '83), pp. 80–86, doi:10.1145/800061.808735.

[14] Lawrence, Jim (1991). "पॉलीटोप वॉल्यूम गणना". Mathematics of Computation. 57 (195): 259–271. doi:10.1090/S0025-5718-1991-1079024-2. ISSN 0025-5718.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]