दूसरा मौलिक रूप

विभेदक ज्यामिति में, दूसरा मौलिक रूप (या आकृति टेंसर) त्रि-आयामी यूक्लिडियन अंतरिक्ष में सतहों के अंतर ज्यामिति के स्पर्शरेखा विमान पर एक द्विघात रूप है, जिसे आमतौर पर निरूपित किया जाता है $\mathrm {I\!I}$ (दो पढ़ें)। पहले मौलिक रूप के साथ, यह सतह के बाह्य आक्रमणकारियों, इसके प्रमुख वक्रता को परिभाषित करने में कार्य करता है। अधिक आम तौर पर, इस तरह के द्विघात रूप को रीमैनियन कई गुना में एक चिकनी विसर्जित सबमेनिफोल्ड के लिए परिभाषित किया गया है।

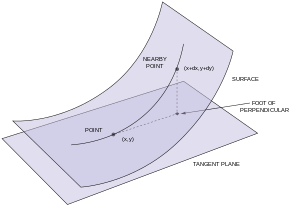
आर में सतह^{3</सुप>}

दूसरे मौलिक रूप की परिभाषा

प्रेरणा

पैरामीट्रिक सतह का दूसरा मौलिक रूप S में R³ का परिचय और अध्ययन कार्ल फ्रेडरिक गॉस ने किया था। पहले मान लीजिए कि सतह दो बार लगातार भिन्न होने वाले फ़ंक्शन का ग्राफ़ है, z = f(x,y), और वह विमान z = 0 मूल बिंदु पर सतह पर स्पर्शरेखा है। तब f और इसके आंशिक डेरिवेटिव के संबंध में x और y (0,0) पर गायब हो जाता है। इसलिए, (0,0) पर f का टेलर विस्तार द्विघात शब्दों से शुरू होता है:

$z=L{\frac {x^{2}}{2}}+Mxy+N{\frac {y^{2}}{2}}+{\text{higher order terms}}\,,$

और निर्देशांक में मूल पर दूसरा मौलिक रूप (x,y) द्विघात रूप है

$L\,dx^{2}+2M\,dx\,dy+N\,dy^{2}\,.$

चिकने बिंदु के लिए P पर S, कोई समन्वय प्रणाली चुन सकता है ताकि विमान z = 0 स्पर्शरेखा है S पर P, और उसी तरह दूसरे मौलिक रूप को परिभाषित करें।

शास्त्रीय संकेतन

सामान्य पैरामीट्रिक सतह के दूसरे मौलिक रूप को निम्नानुसार परिभाषित किया गया है। होने देना r = r(u,v) किसी सतह का नियमित पैरामीट्रिज़ेशन हो R³, कहाँ r दो वेरिएबल्स का एक स्मूद वेक्टर-मूल्यवान फ़ंक्शन है। के आंशिक डेरिवेटिव को निरूपित करना आम है r इसके संबंध में u और v द्वारा r_u और r_v. पैरामीट्रिजेशन की नियमितता का मतलब है कि r_u और r_v किसी के लिए रैखिक रूप से स्वतंत्र हैं (u,v) के डोमेन में r, और इसलिए स्पर्शरेखा तल को फैलाते हैं S प्रत्येक बिंदु पर। समान रूप से, क्रॉस उत्पाद r_u × r_v सतह के लिए सामान्य एक शून्येतर सदिश है। parametrization इस प्रकार इकाई सामान्य वैक्टर के एक क्षेत्र को परिभाषित करता है n:

$\mathbf {n} ={\frac {\mathbf {r} _{u}\times \mathbf {r} _{v}}{|\mathbf {r} _{u}\times \mathbf {r} _{v}|}}\,.$

दूसरा मौलिक रूप आमतौर पर लिखा जाता है

$\mathrm {I\!I} =L\,du^{2}+2M\,du\,dv+N\,dv^{2}\,,$

आधार में इसका मैट्रिक्स {{math|{r_u, r_v}}स्पर्शरेखा तल का } है

${\begin{bmatrix}L&M\\M&N\end{bmatrix}}\,.$

गुणांक L, M, N पैरामीट्रिक में दिए गए बिंदु पर uv-प्लेन के दूसरे आंशिक डेरिवेटिव के अनुमानों द्वारा दिए गए हैं r उस बिंदु पर सामान्य रेखा पर S और निम्नानुसार डॉट उत्पाद की सहायता से गणना की जा सकती है:

$L=\mathbf {r} _{uu}\cdot \mathbf {n} \,,\quad M=\mathbf {r} _{uv}\cdot \mathbf {n} \,,\quad N=\mathbf {r} _{vv}\cdot \mathbf {n} \,.$

हेसियन मैट्रिक्स के एक हस्ताक्षरित दूरी समारोह के लिए H, दूसरे मूलभूत रूप के गुणांकों की गणना निम्नानुसार की जा सकती है:

$L=-\mathbf {r} _{u}\cdot \mathbf {H} \cdot \mathbf {r} _{u}\,,\quad M=-\mathbf {r} _{u}\cdot \mathbf {H} \cdot \mathbf {r} _{v}\,,\quad N=-\mathbf {r} _{v}\cdot \mathbf {H} \cdot \mathbf {r} _{v}\,.$

भौतिक विज्ञानी का अंकन

सामान्य पैरामीट्रिक सतह का दूसरा मौलिक रूप S को इस प्रकार परिभाषित किया गया है।

होने देना r = r(u¹,u²) किसी सतह का नियमित पैरामीट्रिज़ेशन हो R³, कहाँ r दो वेरिएबल्स का एक स्मूद वेक्टर-वैल्यू फंक्शन है। के आंशिक डेरिवेटिव को निरूपित करना आम है r इसके संबंध में u^α द्वारा r_α, α = 1, 2. पैरामीट्रिजेशन की नियमितता का मतलब है कि r₁ और r₂ किसी के लिए रैखिक रूप से स्वतंत्र हैं (u¹,u²) के डोमेन में r, और इसलिए स्पर्शरेखा तल को फैलाते हैं S प्रत्येक बिंदु पर। समान रूप से, क्रॉस उत्पाद r₁ × r₂ सतह के लिए सामान्य एक शून्येतर सदिश है। parametrization इस प्रकार इकाई सामान्य वैक्टर के एक क्षेत्र को परिभाषित करता है n:

$\mathbf {n} ={\frac {\mathbf {r} _{1}\times \mathbf {r} _{2}}{|\mathbf {r} _{1}\times \mathbf {r} _{2}|}}\,.$

दूसरा मौलिक रूप आमतौर पर लिखा जाता है

$\mathrm {I\!I} =b_{\alpha \beta }\,du^{\alpha }\,du^{\beta }\,.$

उपरोक्त समीकरण आइंस्टीन संकेतन का उपयोग करता है।

गुणांक b_αβ पैरामीट्रिक में दिए गए बिंदु पर u¹u²-प्लेन के दूसरे आंशिक डेरिवेटिव के अनुमानों द्वारा दिए गए हैं r उस बिंदु पर सामान्य रेखा पर S और सामान्य वेक्टर के संदर्भ में गणना की जा सकती है n निम्नलिखित नुसार:

$b_{\alpha \beta }=r_{\,\alpha \beta }^{\ \ \,\gamma }n_{\gamma }\,.$

== रीमैनियन मैनिफोल्ड == में हाइपरसफेस

यूक्लिडियन अंतरिक्ष में, दूसरा मौलिक रूप किसके द्वारा दिया गया है

$\mathrm {I\!I} (v,w)=-\langle d\nu (v),w\rangle \nu$

कहाँ $\nu$ गॉस मानचित्र है, और $d\nu$ का पुशफॉरवर्ड (अंतर)। $\nu$ एक सदिश-मूल्य अंतर रूप के रूप में माना जाता है, और कोष्ठक यूक्लिडियन अंतरिक्ष के मीट्रिक टेंसर को दर्शाते हैं।

अधिक आम तौर पर, रिमेंनियन मैनिफोल्ड पर, दूसरा मौलिक रूप आकार ऑपरेटर का वर्णन करने का एक समान तरीका है (द्वारा चिह्नित) S) हाइपरसफेस का,

$\mathrm {I} \!\mathrm {I} (v,w)=\langle S(v),w\rangle n=-\langle \nabla _{v}n,w\rangle n=\langle n,\nabla _{v}w\rangle n\,,$

कहाँ ∇_vw एम्बिएंट मैनिफोल्ड के सहसंयोजक व्युत्पन्न को दर्शाता है और n हाइपरसफेस पर सामान्य वैक्टर का क्षेत्र। (यदि संबंध संबंध मरोड़ टेंसर | मरोड़-मुक्त है, तो दूसरा मौलिक रूप सममित है।)

दूसरे मौलिक रूप का संकेत दिशा की पसंद पर निर्भर करता है n (जिसे हाइपरसफेस का सह-अभिविन्यास कहा जाता है - यूक्लिडियन अंतरिक्ष में सतहों के लिए, यह समान रूप से सतह की उन्मुखता के विकल्प द्वारा दिया जाता है)।

मनमाने codimension का सामान्यीकरण

दूसरे मौलिक रूप को मनमाना कोडिमेंशन के लिए सामान्यीकृत किया जा सकता है। उस मामले में यह सामान्य बंडल में मूल्यों के साथ स्पर्शरेखा स्थान पर द्विघात रूप है और इसे इसके द्वारा परिभाषित किया जा सकता है

$\mathrm {I\!I} (v,w)=(\nabla _{v}w)^{\bot }\,,$

कहाँ $(\nabla _{v}w)^{\bot }$ सहसंयोजक व्युत्पन्न के ऑर्थोगोनल प्रक्षेपण को दर्शाता है $\nabla _{v}w$ सामान्य बंडल पर।

यूक्लिडियन अंतरिक्ष में, सबमनीफोल्ड के रीमैन वक्रता टेन्सर को निम्न सूत्र द्वारा वर्णित किया जा सकता है:

$\langle R(u,v)w,z\rangle =\langle \mathrm {I} \!\mathrm {I} (u,z),\mathrm {I} \!\mathrm {I} (v,w)\rangle -\langle \mathrm {I} \!\mathrm {I} (u,w),\mathrm {I} \!\mathrm {I} (v,z)\rangle .$

इसे गॉस-कोडैज़ी समीकरण कहा जाता है, क्योंकि इसे गॉस के प्रमेय एग्रेगियम के सामान्यीकरण के रूप में देखा जा सकता है।

सामान्य रीमैनियन मैनिफोल्ड्स के लिए परिवेश स्थान की वक्रता को जोड़ना होगा; अगर N एक रीमैनियन मैनिफोल्ड में एम्बेडेड मैनिफोल्ड है (M,g) फिर वक्रता टेन्सर R_N का N प्रेरित मीट्रिक के साथ दूसरे मौलिक रूप का उपयोग करके व्यक्त किया जा सकता है और R_M, की वक्रता टेंसर M:

$\langle R_{N}(u,v)w,z\rangle =\langle R_{M}(u,v)w,z\rangle +\langle \mathrm {I} \!\mathrm {I} (u,z),\mathrm {I} \!\mathrm {I} (v,w)\rangle -\langle \mathrm {I} \!\mathrm {I} (u,w),\mathrm {I} \!\mathrm {I} (v,z)\rangle \,.$

यह भी देखें

• पहला मौलिक रूप
• गॉसियन वक्रता
• गॉस-कोडैज़ी समीकरण
• आकार ऑपरेटर
• तीसरा मौलिक रूप
• टॉटोलॉजिकल वन-फॉर्म

संदर्भ

• Guggenheimer, Heinrich (1977). "Chapter 10. Surfaces". Differential Geometry. Dover. ISBN 0-486-63433-7.
• Kobayashi, Shoshichi & Nomizu, Katsumi (1996). Foundations of Differential Geometry, Vol. 2 (New ed.). Wiley-Interscience. ISBN 0-471-15732-5.
• Spivak, Michael (1999). A Comprehensive introduction to differential geometry (Volume 3). Publish or Perish. ISBN 0-914098-72-1.

बाहरी संबंध

• Steven Verpoort (2008) Geometry of the Second Fundamental Form: Curvature Properties and Variational Aspects from Katholieke Universiteit Leuven.