निश्चित बिंदु (गणित)

तीन निश्चित बिंदुओं वाला एक फ़ंक्शन

एक निश्चित बिंदु (कभी-कभी फिक्सपॉइंट को छोटा किया जाता है, जिसे एक अपरिवर्तनीय बिंदु भी कहा जाता है) एक मान है जो किसी दिए गए परिवर्तन के तहत नहीं बदलता है। विशेष रूप से, गणित में, एक फ़ंक्शन (गणित) का एक निश्चित बिंदु एक तत्व है जिसे फ़ंक्शन द्वारा स्वयं मैप किया जाता है।

भौतिकी में, निश्चित बिंदु शब्द एक ऐसे तापमान को संदर्भित कर सकता है जिसे एक प्रतिलिपि प्रस्तुत करने योग्य संदर्भ बिंदु के रूप में इस्तेमाल किया जा सकता है, जिसे आमतौर पर एक चरण संक्रमण या ट्रिपल बिंदु द्वारा परिभाषित किया जाता है।

किसी फ़ंक्शन का निश्चित बिंदु

औपचारिक रूप से, $c$ एक समारोह का एक निश्चित बिंदु है $f$ अगर $c$ एक फ़ंक्शन के डोमेन और कोडोमेन दोनों के अंतर्गत आता है $f$ , और $f (c) = c$ .

उदाहरण के लिए, यदि $f$ द्वारा वास्तविक संख्याओं पर परिभाषित किया गया है

f(x)=x^{2}-3x+4,

तो 2 का एक निश्चित बिंदु है

f

, क्योंकि

f (2) = 2

.

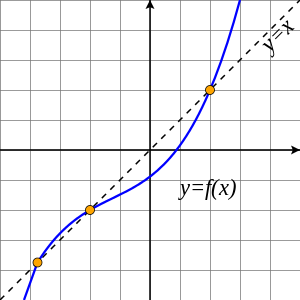
सभी कार्यों के निश्चित बिंदु नहीं होते हैं: उदाहरण के लिए, $f (x) = x + 1$ , के बाद से कोई निश्चित बिंदु नहीं है $x$ के बराबर कभी नहीं होता $x + 1$ किसी भी वास्तविक संख्या के लिए। चित्रमय शब्दों में, एक निश्चित बिंदु $x$ मतलब बिंदु $(x, f (x))$ लाइन पर है $y = x$ , या दूसरे शब्दों में किसी फ़ंक्शन का ग्राफ़ $f$ उस रेखा के साथ एक बिंदु समान है।

फिक्स्ड-पॉइंट पुनरावृत्ति

संख्यात्मक विश्लेषण में, निश्चित-बिंदु पुनरावृत्ति एक फ़ंक्शन के निश्चित बिंदुओं की गणना करने की एक विधि है। विशेष रूप से, एक समारोह दिया $f$ एक ही डोमेन और कोडोमेन के साथ, एक बिंदु $x_{0}$ के अधिकार क्षेत्र में $f$ , निश्चित-बिंदु पुनरावृत्ति है

x_{n+1}=f(x_{n}),\,n=0,1,2,\dots

जो क्रम को जन्म देता है

x_{0},x_{1},x_{2},\dots

पुनरावृत्त फ़ंक्शन अनुप्रयोगों की

x_{0},f(x_{0}),f(f(x_{0})),\dots

जिसे (गणित) को एक बिंदु तक सीमित करने की आशा की जाती है

x

. अगर

f

निरंतर है, तो कोई सिद्ध कर सकता है कि प्राप्त

x

का निश्चित बिन्दु है

f

.

फ़ंक्शन के पुनरावृत्त फ़ंक्शन की सीमित संख्या के बाद समान मान पर वापस आने वाले बिंदुओं को आवधिक बिंदु कहा जाता है। एक निश्चित बिंदु एक आवधिक बिंदु है जिसकी अवधि एक के बराबर होती है।

एक समूह क्रिया का निश्चित बिंदु

बीजगणित में, एक समूह G के लिए एक समूह क्रिया के साथ सेट X पर कार्य करता है $\cdot$ , एक्स में एक्स को जी का एक निश्चित बिंदु कहा जाता है $g\cdot x=x$ .

निश्चित-बिंदु उपसमूह $G^{f}$ एक समूह (गणित) के automorphism एफ का जी जी का उपसमूह है:

G^{f}=\{g\in G\mid f(g)=g\}.

इसी तरह फिक्स्ड-पॉइंट सबरिंग

R^{f}

एक वलय (गणित) के एक ऑटोमोर्फिज्म f का f, f के निश्चित बिंदुओं का उप-वलय है, अर्थात

R^{f}=\{r\in R\mid f(r)=r\}.

गैलोज़ सिद्धांत में, फील्ड ऑटोमोर्फिज्म के सेट के निश्चित बिंदुओं का सेट एक फ़ील्ड (गणित) है जिसे ऑटोमोर्फिज़्म के सेट का निश्चित फ़ील्ड कहा जाता है।

टोपोलॉजिकल फिक्स्ड पॉइंट प्रॉपर्टी

एक टोपोलॉजिकल स्पेस $X$ कहा जाता है कि किसी निरंतर कार्य के लिए निश्चित बिंदु संपत्ति (एफपीपी) है

f\colon X\to X

वहां मौजूद $x\in X$ ऐसा है कि $f(x)=x$ .

एफपीपी एक टोपोलॉजिकल इनवेरिएंट है, यानी किसी भी होमियोमोर्फिज्म द्वारा संरक्षित है। एफपीपी किसी भी रिट्रेक्शन (टोपोलॉजी) द्वारा भी संरक्षित है।

ब्रोवर फिक्स्ड-पॉइंट प्रमेय के अनुसार, यूक्लिडियन अंतरिक्ष के प्रत्येक कॉम्पैक्ट जगह और उत्तल सेट सबसेट में एफपीपी है। अकेले कॉम्पैक्टनेस का मतलब एफपीपी नहीं है और उत्तलता भी एक स्थलीय संपत्ति नहीं है, इसलिए यह पूछना समझ में आता है कि एफपीपी को टोपोलॉजिकल रूप से कैसे चित्रित किया जाए। 1932 में करोल बोरसुक ने पूछा कि क्या FPP को धारण करने के लिए अनुबंधित स्थान के साथ कॉम्पैक्टनेस एक आवश्यक और पर्याप्त शर्त हो सकती है। समस्या 20 वर्षों तक खुली थी जब तक किनोशिता द्वारा अनुमान को अस्वीकृत नहीं किया गया था, जिन्होंने एफपीपी के बिना एक कॉम्पैक्ट अनुबंधित स्थान का उदाहरण पाया।^[1]

आंशिक आदेशों के निश्चित बिंदु

डोमेन सिद्धांत में, निश्चित बिंदुओं की धारणा और शब्दावली को आंशिक क्रम में सामान्यीकृत किया जाता है। चलो ≤ एक सेट एक्स पर एक आंशिक क्रम हो और चलो f: एक्स → एक्स एक्स पर एक फ़ंक्शन हो। फिर एक 'उपसर्ग बिंदु' (जिसे 'पूर्व-निर्धारित बिंदु' भी कहा जाता है, जिसे कभी-कभी 'उपसर्ग बिंदु' या 'पूर्व-निर्धारण बिंदु' के रूप में संक्षिप्त किया जाता है ')^{[citation needed]} f का कोई p ऐसा है कि f(p) ≤ p. अनुरूप रूप से, f का एक पोस्टफिक्स्ड बिंदु कोई भी p है जैसे कि p ≤ f(p)।^[2] विपरीत प्रयोग कभी-कभी प्रकट होता है।^[3] एक निश्चित बिंदु एक बिंदु है जो एक उपसर्ग बिंदु और एक प्रत्यय बिंदु दोनों है। Prefixpoints और postfixpoints के सैद्धांतिक कंप्यूटर विज्ञान में अनुप्रयोग हैं।^[4]

कम से कम निश्चित बिंदु

आदेश सिद्धांत में, आंशिक रूप से ऑर्डर किए गए सेट (पॉसेट) से फ़ंक्शन (गणित) का कम से कम निश्चित बिंदु निश्चित बिंदु है जो पोसेट के क्रम के अनुसार एक दूसरे निश्चित बिंदु से कम है। एक फ़ंक्शन के लिए कम से कम निश्चित बिंदु होना आवश्यक नहीं है, लेकिन यदि ऐसा होता है तो कम से कम निश्चित बिंदु अद्वितीय होता है।

नास्टर-टार्स्की प्रमेय को व्यक्त करने का एक तरीका यह कहना है कि एक पूर्ण जाली पर एक मोनोटोन समारोह में कम से कम फिक्सप्वाइंट होता है जो इसके कम से कम प्रीफिक्सपॉइंट के साथ मेल खाता है (और इसी तरह इसका सबसे बड़ा फिक्सपॉइंट इसके सबसे बड़े कम से कम फिक्सपॉइंट साथ मेल खाता है)।^[5]

फिक्स्ड-पॉइंट कॉम्बिनेटर

कंप्यूटर विज्ञान के लिए संयोजी तर्क में, एक निश्चित-बिंदु संयोजी एक उच्च-क्रम फ़ंक्शन है ${\textsf {fix}}$ जो अपने तर्क कार्य का एक निश्चित बिंदु लौटाता है, यदि कोई मौजूद है। औपचारिक रूप से, यदि फ़ंक्शन f में एक या अधिक निश्चित बिंदु हैं, तो

{\textsf {fix}}\ f=f\ ({\textsf {fix}}\ f)\ ,

फिक्स्ड-पॉइंट लॉजिक्स

गणितीय तर्क में, फिक्स्ड-पॉइंट लॉजिक्स क्लासिकल प्रेडिकेट लॉजिक के विस्तार होते हैं जिन्हें रिकर्सन व्यक्त करने के लिए पेश किया गया है। उनका विकास वर्णनात्मक जटिलता सिद्धांत और डेटाबेस क्वेरी भाषाओं के साथ उनके संबंध, विशेष रूप से Datalog से प्रेरित है।

फिक्स्ड-पॉइंट प्रमेय

एक निश्चित-बिंदु प्रमेय एक परिणाम है जो कहता है कि कम से कम एक निश्चित बिंदु मौजूद है, कुछ सामान्य स्थिति के तहत।^[6] कुछ लेखकों का दावा है कि इस तरह के परिणाम गणित में सबसे अधिक उपयोगी हैं।^[7]

अनुप्रयोग

कई क्षेत्रों में, संतुलन या स्थिरता सिद्धांत मूलभूत अवधारणाएं हैं जिन्हें निश्चित बिंदुओं के संदर्भ में वर्णित किया जा सकता है। कुछ उदाहरण अनुसरण करते हैं।

प्रोजेक्टिव ज्यामिति में, प्रोजेक्टिविटी के एक निश्चित बिंदु को दोहरा बिंदु कहा गया है।^[8]^[9]
अर्थशास्त्र में, खेल सिद्धांत का नैश संतुलन गेम की सर्वश्रेष्ठ प्रतिक्रिया का एक निश्चित बिंदु है। जॉन फोर्ब्स नैश जूनियर ने अपने सेमिनल पेपर के लिए अब निश्चित बिंदु प्रमेय का फायदा उठाया जिसने उन्हें अर्थशास्त्र में नोबेल पुरस्कार जीता।
भौतिकी में, चरण संक्रमण में अधिक सटीक रूप से, एक अस्थिर निश्चित बिंदु के पास रैखिकीकरण ने केनेथ जी विल्सन के नोबेल पुरस्कार विजेता कार्य को पुनर्सामान्यीकरण समूह का आविष्कार करने और शब्द महत्वपूर्ण घटना के गणितीय स्पष्टीकरण के लिए प्रेरित किया है।^[10]^[11]
प्रोग्रामिंग भाषा संकलनकर्ता प्रोग्राम एनालिसिस के लिए फिक्स्ड पॉइंट कंप्यूटेशंस का इस्तेमाल करते हैं, उदाहरण के लिए डेटा प्रवाह विश्लेषण में, जो अक्सर कोड ऑप्टिमाइज़ेशन (कंप्यूटर साइंस) के लिए जरूरी होता है। वे सामान्य कार्यक्रम विश्लेषण पद्धति सार व्याख्या द्वारा उपयोग की जाने वाली मूल अवधारणा भी हैं।^[12]
प्रकार सिद्धांत में, फिक्स्ड-पॉइंट कॉम्बिनेटर अनटाइप्ड लैम्ब्डा कैलकुलस में रिकर्सिव फ़ंक्शंस की परिभाषा की अनुमति देता है।
सभी वेब पेजों के पृष्ठ रैंक मूल्यों का वेक्टर वर्ल्ड वाइड वेब की लिंक संरचना से प्राप्त रैखिक परिवर्तन का निश्चित बिंदु है।
मार्कोव श्रृंखला का स्थिर वितरण एक चरण संक्रमण संभाव्यता समारोह का निश्चित बिंदु है।
तर्कशास्त्री शाऊल कृपके सत्य के अपने प्रभावशाली सिद्धांत में निश्चित बिंदुओं का उपयोग करते हैं। वह दिखाता है कि कैसे एक आंशिक रूप से परिभाषित सत्य विधेय उत्पन्न कर सकता है (एक जो समस्याग्रस्त वाक्यों के लिए अपरिभाषित रहता है जैसे कि यह वाक्य सत्य नहीं है), पुनरावर्ती रूप से सत्य को एक भाषा के खंड से शुरू करके परिभाषित करता है जिसमें शब्द की कोई घटना नहीं होती है, और तब तक जारी रहता है जब तक कि प्रक्रिया किसी भी नए परिभाषित वाक्यों को उत्पन्न करना बंद कर देती है। (यह चरणों का एक गणनीय सेट लेता है।) यानी, एक भाषा L के लिए, L′ (पढ़ें L-प्राइम ) को L में जोड़कर उत्पन्न भाषा होने दें, L में प्रत्येक वाक्य S के लिए, वाक्य S सत्य है। L' L होने पर एक निश्चित बिंदु पर पहुँच जाता है; इस बिंदु पर यह वाक्य सत्य नहीं है जैसे वाक्य अपरिभाषित रहते हैं, इसलिएशाऊल क्रिप्के के अनुसार, सिद्धांत एक प्राकृतिक भाषा के लिए उपयुक्त है जिसमें अपनी स्वयं की सत्य विधेय शामिल है।

यह भी देखें

क्रमपरिवर्तन के चक्र और निश्चित बिंदु
आइजन्वेक्टर
संतुलन बिंदु
मोबियस ट्रांसफॉर्मेशन#फिक्स्ड पॉइंट्स|मोबियस ट्रांसफॉर्मेशन के फिक्स्ड पॉइंट्स
निष्क्रियता
विश्लेषणात्मक कार्यों की अनंत रचनाएँ
अपरिवर्तनीय (गणित)

↑ Kinoshita, S. (1953). "On Some Contractible Continua without Fixed Point Property". Fund. Math. 40 (1): 96–98. doi:10.4064/fm-40-1-96-98. ISSN 0016-2736.
↑ Smyth, Michael B.; Plotkin, Gordon D. (1982). "The Category-Theoretic Solution of Recursive Domain Equations" (PDF). Proceedings, 18th IEEE Symposium on Foundations of Computer Science. SIAM Journal of Computing (volume 11). pp. 761–783. doi:10.1137/0211062.
↑ Patrick Cousot; Radhia Cousot (1979). "Constructive Versions of Tarski's Fixed Point Theorems" (PDF). Pacific Journal of Mathematics. 82 (1): 43–57. doi:10.2140/pjm.1979.82.43.
↑ Yde Venema (2008) Lectures on the Modal μ-calculus Archived March 21, 2012, at the Wayback Machine
↑ Yde Venema (2008) Lectures on the Modal μ-calculus Archived March 21, 2012, at the Wayback Machine
↑ Brown, R. F., ed. (1988). Fixed Point Theory and Its Applications. American Mathematical Society. ISBN 0-8218-5080-6.
↑ Dugundji, James; Granas, Andrzej (2003). Fixed Point Theory. Springer-Verlag. ISBN 0-387-00173-5.
↑ Coxeter, H. S. M. (1942). Non-Euclidean Geometry. University of Toronto Press. p. 36.
↑ G. B. Halsted (1906) Synthetic Projective Geometry, page 27
↑ Wilson, Kenneth G. (1971). "Renormalization Group and Critical Phenomena. I. Renormalization Group and the Kadanoff Scaling Picture". Physical Review B. 4 (9): 3174–3183. Bibcode:1971PhRvB...4.3174W. doi:10.1103/PhysRevB.4.3174.
↑ Wilson, Kenneth G. (1971). "Renormalization Group and Critical Phenomena. II. Phase-Space Cell Analysis of Critical Behavior". Physical Review B. 4 (9): 3184–3205. Bibcode:1971PhRvB...4.3184W. doi:10.1103/PhysRevB.4.3184.
↑ "P. Cousot & R. Cousot, Abstract interpretation: A unified lattice model for static analysis of programs by construction or approximation of fixpoints".

बाहरी संबंध

An Elegant Solution for Drawing a Fixed Point

[1] Kinoshita, S. (1953). "On Some Contractible Continua without Fixed Point Property". Fund. Math. 40 (1): 96–98. doi:10.4064/fm-40-1-96-98. ISSN 0016-2736.

[SmythPlotkin1982-2] Smyth, Michael B.; Plotkin, Gordon D. (1982). "The Category-Theoretic Solution of Recursive Domain Equations" (PDF). Proceedings, 18th IEEE Symposium on Foundations of Computer Science. SIAM Journal of Computing (volume 11). pp. 761–783. doi:10.1137/0211062.

[CousotCousot1979-3] Patrick Cousot; Radhia Cousot (1979). "Constructive Versions of Tarski's Fixed Point Theorems" (PDF). Pacific Journal of Mathematics. 82 (1): 43–57. doi:10.2140/pjm.1979.82.43.

[4] Yde Venema (2008) Lectures on the Modal μ-calculus Archived March 21, 2012, at the Wayback Machine

[5] Yde Venema (2008) Lectures on the Modal μ-calculus Archived March 21, 2012, at the Wayback Machine

[6] Brown, R. F., ed. (1988). Fixed Point Theory and Its Applications. American Mathematical Society. ISBN 0-8218-5080-6.

[7] Dugundji, James; Granas, Andrzej (2003). Fixed Point Theory. Springer-Verlag. ISBN 0-387-00173-5.

[8] Coxeter, H. S. M. (1942). Non-Euclidean Geometry. University of Toronto Press. p. 36.

[9] G. B. Halsted (1906) Synthetic Projective Geometry, page 27

[10] Wilson, Kenneth G. (1971). "Renormalization Group and Critical Phenomena. I. Renormalization Group and the Kadanoff Scaling Picture". Physical Review B. 4 (9): 3174–3183. Bibcode:1971PhRvB...4.3174W. doi:10.1103/PhysRevB.4.3174.

[11] Wilson, Kenneth G. (1971). "Renormalization Group and Critical Phenomena. II. Phase-Space Cell Analysis of Critical Behavior". Physical Review B. 4 (9): 3184–3205. Bibcode:1971PhRvB...4.3184W. doi:10.1103/PhysRevB.4.3184.

[12] "P. Cousot & R. Cousot, Abstract interpretation: A unified lattice model for static analysis of programs by construction or approximation of fixpoints".

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]