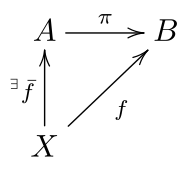प्रक्षेपण (गणित)

गणित में, एक प्रक्षेपण एक उपसमूह (या उप-संरचना) में एक [[सबसेट (गणित)]] (या अन्य गणितीय संरचना) का एक फ़ंक्शन (गणित) है, जो कि फ़ंक्शन रचना के लिए इसके वर्ग के बराबर है, यानी, जो कि idempotent है।एक प्रक्षेपण के एक उप -समूह के लिए प्रतिबंध (गणित) को प्रक्षेपण भी कहा जाता है, भले ही idempotence संपत्ति खो गई हो। एक प्रक्षेपण का एक रोजमर्रा का उदाहरण एक विमान (कागज की शीट) पर छाया की कास्टिंग है: एक बिंदु का प्रक्षेपण कागज की शीट पर इसकी छाया है, और कागज की शीट पर एक बिंदु का प्रक्षेपण (छाया) यह है किखुद को (idempotency)।तीन आयामी क्षेत्र की छाया एक बंद डिस्क है।मूल रूप से, प्रक्षेपण की धारणा को यूक्लिडियन ज्यामिति में पेश किया गया था, जिसमें छाया उदाहरण की तरह एक विमान पर तीन आयामी यूक्लिडियन स्पेस के प्रक्षेपण को निरूपित किया गया था।इस तरह के दो मुख्य अनुमान हैं:

एक विमान या केंद्रीय प्रक्षेपण पर एक बिंदु से प्रक्षेपण: यदि C एक बिंदु है, जिसे प्रक्षेपण का केंद्र कहा जाता है, तो एक विमान पर C से अलग एक बिंदु P का प्रक्षेपण है।शामिल नहीं है C विमान के साथ लाइन (ज्यामिति) CP का चौराहा है।अंक p जैसे कि लाइन cp समानांतर (ज्यामिति) विमान के लिए समानांतर (ज्यामिति) है, प्रक्षेपण द्वारा कोई छवि नहीं है, लेकिन एक अक्सर कहता है कि वे विमान के अनंत पर एक बिंदु पर प्रोजेक्ट करते हैं (देखेंइस शब्दावली की औपचारिकता के लिए प्रोजेक्टिव ज्यामिति)।बिंदु C का प्रक्षेपण स्वयं परिभाषित नहीं है।
एक विमान या समानांतर प्रक्षेपण पर एक दिशा डी के समानांतर प्रक्षेपण: एक बिंदु पी की छवि डी के समानांतर रेखा के विमान के साथ चौराहा है।पी।देखना Affine space § Projection एक सटीक परिभाषा के लिए, किसी भी आयाम के लिए सामान्यीकृत।^{[citation needed]}

गणित में प्रक्षेपण की अवधारणा एक बहुत पुरानी है, और सबसे अधिक संभावना है कि जमीन पर वास्तविक दुनिया की वस्तुओं द्वारा डाली गई छाया की घटना में इसकी जड़ें हैं।इस अल्पविकसित विचार को परिष्कृत और अमूर्त किया गया था, पहले एक ज्यामिति संदर्भ में और बाद में गणित की अन्य शाखाओं में।समय के साथ अवधारणा के विभिन्न संस्करण विकसित हुए, लेकिन आज, पर्याप्त रूप से अमूर्त सेटिंग में, हम इन विविधताओं को एकजुट कर सकते हैं।^{[citation needed]} नक्शानवीसी में, एक मानचित्र प्रक्षेपण एक विमान पर पृथ्वी की सतह के एक हिस्से का एक नक्शा है, जो कुछ मामलों में, लेकिन हमेशा नहीं, उपरोक्त अर्थ में एक प्रक्षेपण का प्रतिबंध है।3 डी अनुमान भी परिप्रेक्ष्य (चित्रमय) के सिद्धांत के आधार पर हैं।^{[citation needed]} दो प्रकार के अनुमानों को एकजुट करने और किसी भी बिंदु के एक केंद्रीय प्रक्षेपण द्वारा छवि को परिभाषित करने की आवश्यकता प्रक्षेपण के केंद्र के अलग -अलग हैं, जो प्रोजेक्टिव ज्यामिति के मूल में हैं।हालांकि, एक प्रक्षेप्य परिवर्तन एक प्रोजेक्टिव स्पेस का एक बड़ा हिस्सा है, एक संपत्ति इस लेख के अनुमानों के साथ साझा नहीं की गई है।^{[citation needed]}

परिभाषा

इस आरेख की कम्यूटिविटी प्रक्षेपण की सार्वभौमिकता है π, किसी भी नक्शे के लिए f और सेट X के लिए।

आम तौर पर, एक मैपिंग जहां एक फ़ंक्शन और संहितात्मक का डोमेन एक ही सेट (गणित) (या गणितीय संरचना) होता है, एक प्रक्षेपण होता है यदि मैपिंग idempotent है, जिसका अर्थ है कि एक प्रक्षेपण अपने साथ अपनी फ़ंक्शन रचना के बराबर है।एक प्रक्षेपण एक मैपिंग का भी उल्लेख कर सकता है जिसमें एक व्युत्क्रम_फंक्शन#Right_inverses है।दोनों धारणाएं दृढ़ता से संबंधित हैं, निम्नानुसार हैं।चलो P को एक सेट A से अपने आप में एक idempotent मानचित्रण करें (इस प्रकार p & p & nbsp; = & nbsp; p) और b & nbsp; = p (a) p की छवि हो।यदि हम π द्वारा मानचित्र p को निरूपित करते हैं, तो एक पर एक मानचित्र के रूप में देखा जाता है और मैं B के इंजेक्टिव फ़ंक्शन को (ताकि p & nbsp; = & nbsp; i π π) में, हमारे पास π ∘ i & nbsp; = & nbsp; id;_B (ताकि π का सही उलटा हो)।इसके विपरीत, यदि π में एक सही व्युत्क्रम है, तो π π i = आईडी_B तात्पर्य है कि मैं π π idempotent है।^{[citation needed]}

अनुप्रयोग

प्रक्षेपण की मूल धारणा को विभिन्न गणितीय स्थितियों के लिए बढ़ाया या सामान्यीकृत किया गया है, अक्सर, लेकिन हमेशा नहीं, ज्यामिति से संबंधित, उदाहरण के लिए:

सेट सिद्धांत में:
- जे द्वारा टाइप किया गया एक ऑपरेशन^Th प्रक्षेपण (सेट सिद्धांत), लिखित प्रोज_j, यह एक तत्व लेता है x = (x₁, ..., x_j, ..., x_n) कार्टेशियन उत्पाद की X₁ × ⋯ × X_j × ⋯ × X_n मूल्य के लिए proj_j(x) = x_j.^[1] यह नक्शा हमेशा समृद्ध होता है और, जब प्रत्येक स्थान X_k एक सामयिक स्थान है, यह नक्शा निरंतरता (टोपोलॉजी) और खुला मानचित्र भी है।^[2]
- एक मानचित्रण जो किसी दिए गए समतुल्यता संबंध के तहत अपने तुल्यता वर्ग में एक तत्व लेता है, को कैनोनिकल प्रक्षेपण के रूप में जाना जाता है।^[3]
- मूल्यांकन मानचित्र एक निश्चित x के लिए मान f (x) के लिए एक फ़ंक्शन f भेजता है।कार्यों का स्थान y^X को कार्टेशियन उत्पाद के साथ पहचाना जा सकता है ${\textstyle \prod _{i\in X}Y}$ , और मूल्यांकन मानचित्र कार्टेशियन उत्पाद से एक प्रक्षेपण मानचित्र है।^{[citation needed]}
संबंध का डेटाबेस और क्वेरी भाषाओं के लिए, प्रक्षेपण (रिलेशनल बीजगणित) के रूप में लिखा गया एक अनियंत्रित ऑपरेशन है $\Pi _{a_{1},\ldots ,a_{n}}(R)$ कहाँ $a_{1},\ldots ,a_{n}$ विशेषता नामों का एक सेट है।इस तरह के प्रक्षेपण के परिणाम को सेट (गणित) के रूप में परिभाषित किया गया है जो कि आर में सभी टपल को सेट तक सीमित कर दिया जाता है $\{a_{1},\ldots ,a_{n}\}$ .^[4]^[5]^[6]^{[verification needed]} R एक संबंध है (डेटाबेस) | डेटाबेस-संबंध।^{[citation needed]}
गोलाकार ज्यामिति में, एक विमान पर एक गोले के प्रक्षेपण का उपयोग टॉलेमी (~ 150) द्वारा उनके प्लानिसफेरियम में किया गया था।^[7] विधि को स्टिरोग्राफिक प्रक्षेपण कहा जाता है और एक गोले के लिए एक विमान स्पर्शरेखा का उपयोग करता है और एक पोल सी टंगेंसी के बिंदु के विपरीत व्यास करता है।सी के अलावा गोले पर कोई भी बिंदु P, P के लिए अनुमानित बिंदु पर विमान को प्रतिच्छेद करने वाली एक लाइन CP निर्धारित करता है।^[8] पत्राचार क्षेत्र को विमान के लिए एक-बिंदु कॉम्पैक्टिफिकेशन बनाता है जब इन्फिनिटी पर एक बिंदु को सी के अनुरूप शामिल किया जाता है, जो अन्यथा विमान पर कोई प्रक्षेपण नहीं होता है।एक सामान्य उदाहरण जटिल विमान है जहां कॉम्पैक्टिफिकेशन रीमैन क्षेत्र से मेल खाता है।वैकल्पिक रूप से, एक क्षेत्र#गोलार्ध को अक्सर सूक्ति प्रक्षेपण का उपयोग करके एक विमान पर पेश किया जाता है।^{[citation needed]}
रैखिक बीजगणित में, एक रैखिक परिवर्तन जो दो बार लागू होने पर अपरिवर्तित रहता है: पी (यू) = पी (पी (यू))।दूसरे शब्दों में, एक idempotent ऑपरेटर।उदाहरण के लिए, मानचित्रण जो तीन आयामों में एक बिंदु (x, y, z) लेता है (x, y, 0) एक प्रक्षेपण है।इस प्रकार का प्रक्षेपण स्वाभाविक रूप से मैपिंग के कोडोमैन के लिए डोमेन के लिए किसी भी संख्या में आयाम n और k k n के लिए सामान्यीकृत करता है।ऑर्थोगोनल प्रक्षेपण, प्रक्षेपण (रैखिक बीजगणित) देखें।ऑर्थोगोनल अनुमानों के मामले में, अंतरिक्ष एक उत्पाद के रूप में एक अपघटन स्वीकार करता है, और प्रक्षेपण ऑपरेटर उस अर्थ में भी एक प्रक्षेपण है।^[9]^[10]^{[verification needed]}
विभेदक टोपोलॉजी में, किसी भी फाइबर बंडल में इसकी परिभाषा के हिस्से के रूप में एक प्रक्षेपण मानचित्र शामिल है।स्थानीय रूप से कम से कम यह नक्शा उत्पाद टोपोलॉजी के अर्थ में एक प्रक्षेपण मानचित्र की तरह दिखता है और इसलिए खुला नक्शा और सर्जिकल है।^{[citation needed]}
टोपोलॉजी में, एक वापसी (टोपोलॉजी) एक सतत मानचित्र (टोपोलॉजी) आर: एक्स → एक्स है जो अपनी छवि पर पहचान के नक्शे को प्रतिबंधित करता है।^[11]^[12] यह एक समान idempotency स्थिति r को संतुष्ट करता है² = r और प्रक्षेपण मानचित्र का सामान्यीकरण माना जा सकता है।एक वापसी की छवि को मूल स्थान की वापसी कहा जाता है।एक वापसी जो पहचान के लिए समलैंगिक है, उसे विरूपण वापसी के रूप में जाना जाता है।इस शब्द का उपयोग श्रेणी सिद्धांत में भी किसी भी विभाजित एपिमोर्फिज्म को संदर्भित करने के लिए किया जाता है।^{[citation needed]}
दूसरे पर एक वेक्टर (ज्यामितीय) का स्केलर दृढ़ (या संकल्प)।^{[citation needed]}
श्रेणी सिद्धांत में, सेट के कार्टेशियन उत्पाद की उपरोक्त धारणा को मनमानी श्रेणी (गणित) के लिए सामान्यीकृत किया जा सकता है।कुछ वस्तुओं के उत्पाद (श्रेणी सिद्धांत) में प्रत्येक कारक के लिए एक विहित प्रोजेक्शन उपदेशता होता है।यह प्रक्षेपण विभिन्न श्रेणियों में कई रूप लेगा।सेट (गणित) के कार्टेशियन उत्पाद से प्रक्षेपण, टोपोलॉजिकल रिक्त स्थान के उत्पाद टोपोलॉजी (जो हमेशा सर्जिकल और ओपन मैप होता है), या समूह के समूहों (गणित) के प्रत्यक्ष उत्पाद से, आदि हालांकि ये आकारिता अक्सर एपिमोर्फिम्स होते हैं औरयहां तक कि सर्जिकल, उन्हें होने की जरूरत नहीं है।^[13]^{[verification needed]}

संदर्भ

↑ "Direct product - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.
↑ Lee, John M. (2012). Introduction to Smooth Manifolds. Graduate Texts in Mathematics. Vol. 218 (Second ed.). p. 606. doi:10.1007/978-1-4419-9982-5. ISBN 978-1-4419-9982-5. Exercise A.32. Suppose $X_{1},\ldots ,X_{k}$ are topological spaces. Show that each projection $\pi _{i}:X_{1}\times \cdots \times X_{k}\to X_{i}$ is an open map.
↑ Brown, Arlen; Pearcy, Carl (1994-12-16). An Introduction to Analysis. Springer Science & Business Media. ISBN 978-0-387-94369-5.
↑ Alagic, Suad (2012-12-06). Relational Database Technology. Springer Science & Business Media. ISBN 978-1-4612-4922-1.
↑ Date, C. J. (2006-08-28). The Relational Database Dictionary: A Comprehensive Glossary of Relational Terms and Concepts, with Illustrative Examples. "O'Reilly Media, Inc.". ISBN 978-1-4493-9115-7.
↑ "Relational Algebra". www.cs.rochester.edu. Archived from the original on 30 January 2004. Retrieved 29 August 2021.
↑ Sidoli, Nathan; Berggren, J. L. (2007). "The Arabic version of Ptolemy's Planisphere or Flattening the Surface of the Sphere: Text, Translation, Commentary" (PDF). Sciamvs. 8. Retrieved 11 August 2021.
↑ "Stereographic projection - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.
↑ "Projection - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.
↑ Roman, Steven (2007-09-20). Advanced Linear Algebra. Springer Science & Business Media. ISBN 978-0-387-72831-5.
↑ "Retraction - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.
↑ "वापस लेना". planetmath.org. Retrieved 2021-08-11.
↑ "Product of a family of objects in a category - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.

अग्रिम पठन

Thomas Craig (1882) A Treatise on Projections from University of Michigan Historical Math Collection.

[1] "Direct product - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.

[2] Lee, John M. (2012). Introduction to Smooth Manifolds. Graduate Texts in Mathematics. Vol. 218 (Second ed.). p. 606. doi:10.1007/978-1-4419-9982-5. ISBN 978-1-4419-9982-5. Exercise A.32. Suppose $X_{1},\ldots ,X_{k}$ are topological spaces. Show that each projection $\pi _{i}:X_{1}\times \cdots \times X_{k}\to X_{i}$ is an open map.

[3] Brown, Arlen; Pearcy, Carl (1994-12-16). An Introduction to Analysis. Springer Science & Business Media. ISBN 978-0-387-94369-5.

[4] Alagic, Suad (2012-12-06). Relational Database Technology. Springer Science & Business Media. ISBN 978-1-4612-4922-1.

[5] Date, C. J. (2006-08-28). The Relational Database Dictionary: A Comprehensive Glossary of Relational Terms and Concepts, with Illustrative Examples. "O'Reilly Media, Inc.". ISBN 978-1-4493-9115-7.

[6] "Relational Algebra". www.cs.rochester.edu. Archived from the original on 30 January 2004. Retrieved 29 August 2021.

[7] Sidoli, Nathan; Berggren, J. L. (2007). "The Arabic version of Ptolemy's Planisphere or Flattening the Surface of the Sphere: Text, Translation, Commentary" (PDF). Sciamvs. 8. Retrieved 11 August 2021.

[8] "Stereographic projection - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.

[9] "Projection - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.

[10] Roman, Steven (2007-09-20). Advanced Linear Algebra. Springer Science & Business Media. ISBN 978-0-387-72831-5.

[11] "Retraction - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.

[12] "वापस लेना". planetmath.org. Retrieved 2021-08-11.

[13] "Product of a family of objects in a category - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

प्रक्षेपण (गणित)

Contents

परिभाषा

अनुप्रयोग

संदर्भ

अग्रिम पठन

Navigation menu

Search