समानता वर्ग

This article is about equivalency in mathematics. For equivalency in music, see equivalence class (music).

सर्वांगसमता (ज्यामिति) तुल्यता संबंध का एक उदाहरण है। सबसे बाएँ दो त्रिभुज सर्वांगसम हैं, जबकि तीसरा और चौथा त्रिभुज यहाँ दिखाए गए किसी अन्य त्रिभुज के सर्वांगसम नहीं हैं। इस प्रकार, पहले दो त्रिभुज एक ही तुल्यता वर्ग में हैं, जबकि तीसरा और चौथा त्रिभुज प्रत्येक अपने-अपने तुल्यता वर्ग में हैं।

गणित में, जब कुछ सेट (गणित) के तत्व $S$ तुल्यता की धारणा है (एक तुल्यता संबंध के रूप में औपचारिक), तो कोई स्वाभाविक रूप से सेट को विभाजित कर सकता है $S$ तुल्यता वर्गों में। इन तुल्यता वर्गों का निर्माण इसलिए किया जाता है ताकि Elements $a$ तथा $b$ समान समकक्ष वर्ग से संबंधित हैं यदि, और केवल यदि, वे समकक्ष हैं।

औपचारिक रूप से, एक सेट दिया $S$ और एक तुल्यता संबंध $\,\sim \,$ पर $S,$ equivalence class एक तत्व का $a$ में $S,$ द्वारा चिह्नित $[a],$ सेट है

$$\{x\in S:x\sim a\}$$

तत्वों के बराबर हैं $a.$ तुल्यता संबंधों के परिभाषित गुणों से यह सिद्ध किया जा सकता है कि तुल्यता वर्ग एक सेट का एक विभाजन बनाते हैं $S.$ यह विभाजन - तुल्यता वर्गों का समुच्चय - कभी-कभी भागफल समुच्चय या भागफल स्थान कहा जाता है $S$ द्वारा $\,\sim \,,$ और द्वारा दर्शाया गया है $S/\sim .$ जब सेट $S$ कुछ संरचना है (जैसे एक समूह (गणित) या एक सामयिक स्थान) और तुल्यता संबंध $\,\sim \,$ इस संरचना के साथ संगत है, भागफल सेट अक्सर अपने मूल सेट से समान संरचना प्राप्त करता है। उदाहरणों में भागफल स्थान (रैखिक बीजगणित), भागफल स्थान (टोपोलॉजी), भागफल समूह, सजातीय स्थान, भागफल वलय, भागफल मोनोइड और भागफल श्रेणी शामिल हैं।

उदाहरण

• यदि $X$ सभी कारों का सेट है, और $\,\sim \,$ यदि तुल्यता संबंध का रंग समान है, तो एक विशेष तुल्यता वर्ग में सभी हरे रंग की कारें शामिल होंगी, और $X/\sim$ सभी कार रंगों के सेट के साथ स्वाभाविक रूप से पहचाना जा सकता है।
• होने देना $X$ एक समतल में सभी आयतों का समुच्चय हो, और $\,\sim \,$ तुल्यता संबंध का क्षेत्रफल , के बराबर है तो प्रत्येक सकारात्मक वास्तविक संख्या के लिए $A,$ क्षेत्रफल वाले सभी आयतों का एक समतुल्य वर्ग होगा $A.$
• पूर्णांकों के समुच्चय पर मॉड्यूलर अंकगणितीय 2 तुल्यता संबंध पर विचार करें, $\mathbb {Z} ,$ ऐसा है कि $x\sim y$ अगर और केवल अगर उनका अंतर $x-y$ एक सम संख्या है। यह संबंध वास्तव में दो तुल्यता वर्गों को जन्म देता है: एक वर्ग में सभी सम संख्याएँ होती हैं, और दूसरे वर्ग में सभी विषम संख्याएँ होती हैं। इस संबंध के तहत एक समकक्ष वर्ग को निरूपित करने के लिए वर्ग के एक सदस्य के चारों ओर वर्ग कोष्ठक का उपयोग करना, $[7],[9],$ तथा $[1]$ सभी एक ही तत्व का प्रतिनिधित्व करते हैं $\mathbb {Z} /\sim .$
• होने देना $X$ पूर्णांकों के क्रमित युग्मों का समुच्चय हो $(a,b)$ गैर शून्य के साथ $b,$ और एक तुल्यता संबंध को परिभाषित करें $\,\sim \,$ पर $X$ ऐसा है कि $(a,b)\sim (c,d)$ अगर और केवल अगर $ad=bc,$ फिर जोड़ी का समकक्ष वर्ग $(a,b)$ परिमेय संख्या से पहचाना जा सकता है $a/b,$ और इस तुल्यता संबंध और इसके तुल्यता वर्गों का उपयोग परिमेय संख्याओं के समुच्चय की औपचारिक परिभाषा देने के लिए किया जा सकता है। किसी भी अभिन्न डोमेन के अंशों के क्षेत्र में एक ही निर्माण को सामान्यीकृत किया जा सकता है।
• यदि $X$ यूक्लिडियन विमान, और कहते हैं, में सभी रेखाएं शामिल हैं $L\sim M$ मतलब कि $L$ तथा $M$ समानांतर रेखाएँ हैं, तो रेखाओं का समूह जो एक दूसरे के समानांतर हैं, एक समतुल्यता वर्ग बनाते हैं, जब तक कि एक समानांतर (ज्यामिति) #Reflexive संस्करण। इस स्थिति में, प्रत्येक तुल्यता वर्ग अनंत पर एक बिंदु निर्धारित करता है।

परिभाषा और अंकन

एक सेट पर एक तुल्यता संबंध $X$ एक द्विआधारी संबंध है $\,\sim \,$ पर $X$ तीन गुणों को संतुष्ट करना:

• $a\sim a$ सभी के लिए $a\in X$ (प्रतिवर्त संबंध),
• $a\sim b$ तात्पर्य $b\sim a$ सभी के लिए $a,b\in X$ (सममित संबंध),
• यदि $a\sim b$ तथा $b\sim c$ फिर $a\sim c$ सभी के लिए $a,b,c\in X$ (सकर्मक संबंध)।

किसी तत्व का समतुल्य वर्ग $a$ अक्सर निरूपित किया जाता है $[a]$ या $[a]_{\sim },$ और सेट के रूप में परिभाषित किया गया है $\{x\in X:a\sim x\}$ तत्वों से संबंधित हैं $a$ द्वारा$\,\sim .$तुल्यता वर्ग शब्द में शब्द वर्ग को आम तौर पर सेट (गणित) के पर्याय के रूप में माना जा सकता है, हालांकि कुछ तुल्यता वर्ग सेट नहीं बल्कि उचित वर्ग हैं। उदाहरण के लिए, समूह समरूपता होना समूह (गणित) पर एक तुल्यता संबंध है, और तुल्यता वर्ग, जिसे तुल्याकारिता वर्ग कहा जाता है, समुच्चय नहीं हैं।

में सभी समकक्ष वर्गों का सेट $X$ तुल्यता संबंध के संबंध में $R$ के रूप में दर्शाया गया है $X/R,$ और कहा जाता है $X$ मॉड्यूलो (गणित) $R$ (याquotient setका $X$ द्वारा $R$). विशेषण नक्शा $x\mapsto [x]$ से $X$ पर $X/R,$ जो प्रत्येक तत्व को उसके तुल्यता वर्ग में मैप करता है, कहलाता हैcanonical surjection, या विहित प्रक्षेपण।

समतुल्यता वर्ग का प्रत्येक तत्व वर्ग की विशेषता है, और इसका प्रतिनिधित्व करने के लिए इस्तेमाल किया जा सकता है। जब ऐसे तत्व को चुना जाता है, तो उसे वर्ग का 'प्रतिनिधि' कहा जाता है। प्रत्येक वर्ग में एक प्रतिनिधि की पसंद एक इंजेक्शन समारोह को परिभाषित करती है $X/R$ प्रति X. चूँकि इसका कार्य संयोजन विहित अनुमान के साथ की पहचान है $X/R,$ श्रेणी सिद्धांत की शब्दावली का उपयोग करते समय इस तरह के इंजेक्शन को धारा (श्रेणी सिद्धांत) कहा जाता है।

कभी-कभी, एक खंड ऐसा होता है जो अन्य की तुलना में अधिक स्वाभाविक होता है। ऐसे में जनप्रतिनिधियों को बुलाया जाता है canonical representatives. उदाहरण के लिए, मॉड्यूलर अंकगणित में, प्रत्येक पूर्णांक के लिए m से अधिक 1, सर्वांगसमता मॉड्यूल m|सर्वांगसमता मॉड्यूल mपूर्णांकों पर एक तुल्यता संबंध है, जिसके लिए दो पूर्णांक हैं a तथा b समतुल्य हैं - इस मामले में, कोई सर्वांगसम कहता है - यदि m विभाजित $a-b;$ यह दर्शाया गया है ${\textstyle a\equiv b{\pmod {m}}.}$ प्रत्येक वर्ग में एक अद्वितीय गैर-ऋणात्मक पूर्णांक होता है जो इससे छोटा होता है $m,$ और ये पूर्णांक विहित प्रतिनिधि हैं।

वर्गों का प्रतिनिधित्व करने के लिए प्रतिनिधियों का उपयोग स्पष्ट रूप से वर्गों को सेट के रूप में मानने से बचने की अनुमति देता है। इस मामले में, किसी तत्व को उसकी कक्षा में मैप करने वाले विहित अनुमान को उस फ़ंक्शन द्वारा प्रतिस्थापित किया जाता है जो किसी तत्व को उसकी कक्षा के प्रतिनिधि के लिए मैप करता है। पिछले उदाहरण में, यह फ़ंक्शन निरूपित किया गया है $a{\bmod {m}},$ और यूक्लिडियन विभाजन के शेष का उत्पादन करता है a द्वारा m.

गुण

हर तत्व $x$ का $X$ समतुल्य वर्ग का सदस्य है $[x].$ हर दो समकक्ष वर्ग $[x]$ तथा $[y]$ या तो समान या असंयुक्त समुच्चय हैं। इसलिए, के सभी समकक्ष वर्गों का सेट $X$ के एक सेट का विभाजन बनाता है $X$: का हर तत्व $X$ एक और केवल एक तुल्यता वर्ग के अंतर्गत आता है। इसके विपरीत, का हर विभाजन $X$ इस तरह से एक तुल्यता संबंध से आता है, जिसके अनुसार $x\sim y$ अगर और केवल अगर $x$ तथा $y$ विभाजन के एक ही सेट से संबंधित हैं। यह एक तुल्यता संबंध के गुणों से अनुसरण करता है कि

$$x\sim y$$

अगर और केवल अगर$[x]=[y].$ दूसरे शब्दों में, अगर $\,\sim \,$ एक सेट पर एक तुल्यता संबंध है $X,$ तथा $x$ तथा $y$ के दो तत्व हैं $X,$ तब ये कथन समतुल्य हैं:

• $x\sim y$
• $[x]=[y]$
• $[x]\cap [y]\neq \emptyset .$

ग्राफिकल प्रतिनिधित्व

7 वर्गों के साथ एक उदाहरण तुल्यता का ग्राफ

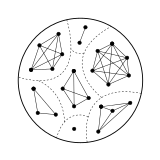
एक अप्रत्यक्ष ग्राफ एक सेट पर किसी सममित संबंध से जुड़ा हो सकता है $X,$ जहां शीर्ष तत्व हैं $X,$ और दो शिखर $s$ तथा $t$ अगर और केवल अगर शामिल हो गए हैं $s\sim t.$ इन रेखांकनों में तुल्यता संबंधों के रेखांकन हैं; उन्हें ग्राफ़ के रूप में चित्रित किया जाता है जैसे कि कनेक्टेड घटक (ग्राफ़ सिद्धांत) क्लिक (ग्राफ़ सिद्धांत) हैं।

अपरिवर्तनीय

यदि $\,\sim \,$ पर एक तुल्यता संबंध है $X,$ तथा $P(x)$ के तत्वों का गुण है $X$ ऐसा कि जब भी $x\sim y,$ $P(x)$ सच है अगर $P(y)$ सच है, तो संपत्ति $P$ का अपरिवर्तनशील (गणित) कहा जाता है $\,\sim \,,$ या संबंध के तहत अच्छी तरह से परिभाषित $\,\sim .$ अक्सर विशेष मामला तब होता है जब $f$ से एक समारोह है $X$ दूसरे सेट के लिए $Y$; यदि $f\left(x_{1}\right)=f\left(x_{2}\right)$ जब भी $x_{1}\sim x_{2},$ फिर $f$ बताया गया class invariant under $\,\sim \,,$ या केवल invariant under $\,\sim .$ यह होता है, उदाहरण के लिए, परिमित समूहों के चरित्र सिद्धांत में। कुछ लेखक संगत का उपयोग करते हैं $\,\sim \,$या सिर्फ सम्मान करता है $\,\sim \,$के तहत अपरिवर्तनीय के बजाय $\,\sim \,$.

कोई भी कार्य (गणित) $f:X\to Y$ वर्ग अपरिवर्तनीय है $\,\sim \,,$ किसके अनुसार $x_{1}\sim x_{2}$ अगर और केवल अगर $f\left(x_{1}\right)=f\left(x_{2}\right).$ का समतुल्य वर्ग $x$ में सभी तत्वों का समुच्चय है $X$ जिसे मैप किया जाता है $f(x),$ वह है, वर्ग $[x]$ का प्रतिलोम चित्र है $f(x).$ इस तुल्यता संबंध को एक फलन के कर्नेल के रूप में जाना जाता है $f.$ अधिक आम तौर पर, एक फ़ंक्शन समकक्ष तर्कों को मैप कर सकता है (तुल्यता संबंध के तहत $\sim _{X}$ पर $X$) समकक्ष मूल्यों के लिए (एक समकक्ष संबंध के तहत $\sim _{Y}$ पर $Y$). ऐसा फलन समतुल्य संबंध से सुसज्जित समुच्चयों का आकार है।

टोपोलॉजी में भागफल स्थान

टोपोलॉजी में, एक कोटिएंट स्पेस (टोपोलॉजी) एक टोपोलॉजिकल स्पेस है, जो तुल्यता वर्गों के सेट पर टोपोलॉजी बनाने के लिए मूल स्थान की टोपोलॉजी का उपयोग करते हुए, टोपोलॉजिकल स्पेस पर एक तुल्यता संबंध के तुल्यता वर्गों के सेट पर बनता है।

अमूर्त बीजगणित में, बीजगणित के अंतर्निहित सेट पर सर्वांगसमता संबंध बीजगणित को संबंध के तुल्यता वर्गों पर एक बीजगणित प्रेरित करने की अनुमति देते हैं, जिसे एक भागफल (सार्वभौमिक बीजगणित) कहा जाता है। रेखीय बीजगणित में, एक भागफल स्थान (रैखिक बीजगणित) एक सदिश स्थान है जो एक भागफल समूह लेकर बनता है, जहां भागफल समरूपता एक रेखीय नक्शा है। विस्तार से, अमूर्त बीजगणित में, भागफल स्थान शब्द का उपयोग भागफल मॉड्यूल, भागफल के छल्ले, भागफल समूह, या किसी भी अंश बीजगणित के लिए किया जा सकता है। हालांकि, अधिक सामान्य मामलों के लिए शब्द का उपयोग अक्सर समूह क्रिया की कक्षाओं के अनुरूप हो सकता है।

एक सेट पर एक समूह क्रिया (गणित) की कक्षाओं को सेट पर क्रिया का भागफल स्थान कहा जा सकता है, विशेषकर जब समूह क्रिया की कक्षाएँ समूह के एक उपसमूह के सही सहसमुच्चय हों, जो की क्रिया से उत्पन्न होती हैं। बाएं अनुवाद द्वारा समूह पर उपसमूह, या क्रमशः बाएं सह समुच्चय दाएं अनुवाद के तहत कक्षाओं के रूप में।

एक टोपोलॉजिकल समूह का एक सामान्य उपसमूह, अनुवाद क्रिया द्वारा समूह पर कार्य करता है, टोपोलॉजी, अमूर्त बीजगणित और समूह क्रियाओं के साथ-साथ एक भागफल स्थान है।

यद्यपि इस शब्द का उपयोग किसी भी तुल्यता संबंध के तुल्यता वर्गों के सेट के लिए किया जा सकता है, संभवतः आगे की संरचना के साथ, शब्द का उपयोग करने का इरादा आम तौर पर एक सेट पर उस प्रकार के तुल्यता संबंध की तुलना करना है $X,$ या तो एक तुल्यता संबंध के लिए जो समान प्रकार की संरचना से तुल्यता वर्गों के सेट पर कुछ संरचना को प्रेरित करता है $X,$ या एक समूह कार्रवाई की कक्षाओं के लिए। समतुल्य संबंध द्वारा संरक्षित संरचना की भावना, और समूह क्रियाओं के तहत अपरिवर्तनीय (गणित) के अध्ययन दोनों, ऊपर दिए गए समतुल्य संबंधों के #Invariants की परिभाषा की ओर ले जाते हैं।

यह भी देखें

• तुल्यता विभाजन, उन आदानों पर कार्यक्रम के व्यवहार के अनुसार संभावित प्रोग्राम इनपुट को तुल्यता वर्गों में विभाजित करने के आधार पर सॉफ़्टवेयर परीक्षण में परीक्षण सेट तैयार करने की एक विधि
• सजातीय स्थान, झूठ समूहों का भागफल स्थान
• Partial equivalence relation
• Quotient by an equivalence relation
• Transversal (combinatorics)

संदर्भ

• Avelsgaard, Carol (1989), Foundations for Advanced Mathematics, Scott Foresman, ISBN 0-673-38152-8
• Devlin, Keith (2004), Sets, Functions, and Logic: An Introduction to Abstract Mathematics (3rd ed.), Chapman & Hall/ CRC Press, ISBN 978-1-58488-449-1
• Maddox, Randall B. (2002), Mathematical Thinking and Writing, Harcourt/ Academic Press, ISBN 0-12-464976-9
• Wolf, Robert S. (1998), Proof, Logic and Conjecture: A Mathematician's Toolbox, Freeman, ISBN 978-0-7167-3050-7

अग्रिम पठन

• Sundstrom (2003), Mathematical Reasoning: Writing and Proof, Prentice-Hall
• Smith; Eggen; St.Andre (2006), A Transition to Advanced Mathematics (6th ed.), Thomson (Brooks/Cole)
• Schumacher, Carol (1996), Chapter Zero: Fundamental Notions of Abstract Mathematics, Addison-Wesley, ISBN 0-201-82653-4
• O'Leary (2003), The Structure of Proof: With Logic and Set Theory, Prentice-Hall
• Lay (2001), Analysis with an introduction to proof, Prentice Hall
• Morash, Ronald P. (1987), Bridge to Abstract Mathematics, Random House, ISBN 0-394-35429-X
• Gilbert; Vanstone (2005), An Introduction to Mathematical Thinking, Pearson Prentice-Hall
• Fletcher; Patty, Foundations of Higher Mathematics, PWS-Kent
• Iglewicz; Stoyle, An Introduction to Mathematical Reasoning, MacMillan
• D'Angelo; West (2000), Mathematical Thinking: Problem Solving and Proofs, Prentice Hall
• Cupillari, The Nuts and Bolts of Proofs, Wadsworth
• Bond, Introduction to Abstract Mathematics, Brooks/Cole
• Barnier; Feldman (2000), Introduction to Advanced Mathematics, Prentice Hall
• Ash, A Primer of Abstract Mathematics, MAA

इस पेज में लापता आंतरिक लिंक की सूची

• अंक शास्त्र
• एक सेट का विभाजन
• टोपोलॉजिकल स्पेस
• भागफल की अंगूठी
• अंशों का क्षेत्र
• समानांतर रेखाएं
• अनंत पर बिंदु
• समरूपता वर्ग
• समारोह रचना
• अनुभाग (श्रेणी सिद्धांत)
• अलग सेट
• जुड़ा हुआ घटक (ग्राफ सिद्धांत)
• क्लिक (ग्राफ सिद्धांत)
• अपरिवर्तनीय (गणित)
• समारोह (गणित)
• उलटी छवि
• किसी फ़ंक्शन का कर्नेल
• आकारिता
• रैखिक नक्शा
• सार बीजगणित
• लीनियर अलजेब्रा
• समान विभाजन

बाहरी संबंध

• Media related to Equivalence classes at Wikimedia Commons