फर्मेट नंबर
| Named after | Pierre de Fermat |
|---|---|
| No. of known terms | 5 |
| Conjectured no. of terms | 5 |
| Subsequence of | Fermat numbers |
| First terms | 3, 5, 17, 257, 65537 |
| Largest known term | 65537 |
| OEIS index | A019434 |
गणित में, एक फर्मेट संख्या, जिसका नाम पियरे डी फर्मेट के नाम पर रखा गया है, जिन्होंने सबसे पहले उनका अध्ययन किया था, वह फॉर्म की एक प्राकृतिक संख्या है
जहाँ n एक गैर-ऋणात्मक पूर्णांक है। पहले कुछ Fermat नंबर हैं:
- 3 (संख्या), 5 (संख्या), 17 (संख्या), 257 (संख्या), 65537 (संख्या), 4294967297, 18446744073709551617, ... (sequence A000215 in the OEIS).
अगर 2k + 1 अभाज्य संख्या है और k > 0, तो k की घात 2 होनी चाहिए, इसलिए 2k + 1 एक फर्मेट संख्या है; ऐसे प्राइम्स को फर्मेट प्राइम्स कहा जाता है। As of 2023[update], केवल ज्ञात Fermat primes हैं F0 = 3, F1 = 5, F2 = 17, F3 = 257, और F4 = 65537 (sequence A019434 in the OEIS); ह्यूरिस्टिक्स का सुझाव है कि अब और नहीं हैं।
मूल गुण
फ़र्मेट संख्याएँ निम्नलिखित पुनरावृत्ति संबंधों को संतुष्ट करती हैं:
एन ≥ 1 के लिए,
के लिए n ≥ 2. इनमें से प्रत्येक संबंध को गणितीय आगमन द्वारा सिद्ध किया जा सकता है। दूसरे समीकरण से, हम गोल्डबैक के प्रमेय (क्रिश्चियन गोल्डबैक के नाम पर) को घटा सकते हैं: कोई दो फर्मेट संख्याएं सहअभाज्य नहीं हैं। इसे देखने के लिए, मान लीजिए 0 ≤ i < j और एफi और एफj एक सामान्य कारक है a > 1. तब a दोनों को विभाजित करता है
और एफj; इसलिए a उनके अंतर को विभाजित करता है, 2. चूँकि a > 1, यह बल a = 2. यह एक विरोधाभास है, क्योंकि प्रत्येक फर्मेट संख्या स्पष्ट रूप से विषम है। एक उपप्रमेय के रूप में, हम अभाज्य संख्याओं की अनंतता का एक और प्रमाण प्राप्त करते हैं: प्रत्येक F के लिएn, एक प्रमुख कारक पी चुनेंn; फिर क्रम {pn} भिन्न अभाज्य संख्याओं का अनंत क्रम है।
और गुण
- किसी भी Fermat अभाज्य को दो pth घातों के अंतर के रूप में व्यक्त नहीं किया जा सकता है, जहाँ p एक विषम अभाज्य है।
- एफ के अपवाद के साथ0 और एफ1, फर्मेट संख्या का अंतिम अंक 7 है।
- सभी Fermat संख्याओं के व्युत्क्रमों का योग (sequence A051158 in the OEIS) अपरिमेय संख्या है। (सोलोमन डब्ल्यू गोलोम्ब, 1963)
प्रधानता
Fermat नंबर और Fermat primes का अध्ययन सबसे पहले Pierre de Fermat ने किया था, जिन्होंने अनुमान लगाया था कि सभी Fermat नंबर प्राइम हैं। दरअसल, पहले पांच फर्मेट नंबर एफ0, ..., एफ4 आसानी से प्रमुख दिखाया जाता है। 1732 में लियोनहार्ड यूलर द्वारा फ़र्मेट के अनुमान का खंडन किया गया जब उन्होंने यह दिखाया
यूलर ने सिद्ध किया कि F का प्रत्येक कारकn रूप होना चाहिए k 2n+1 + 1 (बाद में सुधार हुआ k 2n+2 + 1 एडवर्ड लुकास द्वारा) के लिए n ≥ 2.
वह 641 एफ का कारक है5 समानता 641 = 2 से घटाया जा सकता है7 × 5 + 1 और 641 = 24 + 54</उप>। यह पहली समानता से अनुसरण करता है कि 27 × 5 ≡ -1 (मॉड 641) और इसलिए (चौथी घात की ओर बढ़ते हुए) कि 228 × 54 ≡ 1 (मॉड 641)। दूसरी ओर, दूसरी समानता का तात्पर्य है कि 54 ≡ −24 (मॉड 641)। इन मॉड्यूलर अंकगणित का अर्थ है कि 232 ≡ −1 (मॉड 641)।
फर्मेट शायद बाद में यूलर द्वारा सिद्ध किए गए कारकों के रूप से अवगत थे, इसलिए यह उत्सुक लगता है कि वह कारक खोजने के लिए सीधी गणना के माध्यम से पालन करने में विफल रहे।[1] एक सामान्य व्याख्या यह है कि फर्मेट ने कम्प्यूटेशनल गलती की।
कोई अन्य ज्ञात Fermat primes F नहीं हैn साथ n > 4, लेकिन बड़े n के लिए Fermat संख्याओं के बारे में बहुत कम जानकारी है।[2] वास्तव में, निम्न में से प्रत्येक एक खुली समस्या है:
- क्या एफn सभी के लिए समग्र संख्या n > 4?
- क्या असीम रूप से कई फर्मेट प्राइम्स हैं? (गोथोल्ड ईसेनस्टीन 1844[3])
- क्या अपरिमित रूप से अनेक यौगिक फ़र्मैट संख्याएँ हैं?
- क्या कोई फ़र्मैट संख्या मौजूद है जो वर्ग-मुक्त संख्या नहीं है | वर्ग-मुक्त?
As of 2014[update], ज्ञातव्य है कि एफn के लिए संयुक्त है 5 ≤ n ≤ 32, हालांकि इनमें से, F के पूर्ण गुणनखंड हैंn लिए ही जाने जाते हैं 0 ≤ n ≤ 11, और इसके लिए कोई ज्ञात प्रमुख कारक नहीं हैं n = 20 और n = 24.[4]संमिश्र के रूप में ज्ञात सबसे बड़ी फर्मेट संख्या F है18233954, और इसका प्रमुख कारक 7 × 218233956 + 1 अक्टूबर 2020 में खोजा गया था।
अनुमानी तर्क
ह्यूरिस्टिक्स का सुझाव है कि एफ4 अंतिम फर्मेट प्राइम है।
अभाज्य संख्या प्रमेय का अर्थ है कि N के आसपास एक उपयुक्त अंतराल में एक यादृच्छिक पूर्णांक प्रायिकता 1 के साथ अभाज्य है / एलएन एन। यदि कोई हेरिस्टिक का उपयोग करता है कि एक फर्मेट संख्या एक ही संभावना के साथ अपने आकार के एक यादृच्छिक पूर्णांक के रूप में प्रमुख है, और वह एफ5, ..., एफ32 संमिश्र हैं, तो F से परे Fermat primes की अपेक्षित संख्या4 (या समकक्ष, एफ से परे32) होना चाहिए
कोई इस संख्या की व्याख्या इस प्रायिकता के लिए ऊपरी सीमा के रूप में कर सकता है कि F से परे एक Fermat अभाज्य है4 मौजूद।
यह तर्क एक कठोर प्रमाण नहीं है। एक बात के लिए, यह माना जाता है कि फर्मेट नंबर बेतरतीब ढंग से व्यवहार करते हैं, लेकिन फर्मेट नंबरों के कारकों में विशेष गुण होते हैं। बोकलान और जॉन एच. कॉनवे ने एक अधिक सटीक विश्लेषण प्रकाशित किया जिसमें यह सुझाव दिया गया कि एक और फ़र्मेट प्राइम होने की संभावना एक अरब में एक से कम है।[5]
समतुल्य शर्तें
होने देना nth Fermat संख्या हो। पेपिन का परीक्षण बताता है कि के लिए n > 0,
- प्रधान है अगर और केवल अगर
इजहार मॉड्यूलो का मूल्यांकन किया जा सकता है घातांक द्वारा वर्ग करके। यह परीक्षण को एक तेज़ बहुपद-समय एल्गोरिथम बनाता है। लेकिन Fermat संख्या इतनी तेज़ी से बढ़ती है कि उनमें से केवल कुछ मुट्ठी भर का ही उचित समय और स्थान में परीक्षण किया जा सकता है।
प्रपत्र की संख्याओं के लिए कुछ परीक्षण हैं k 2m + 1, जैसे कि फ़र्मेट संख्या के कारक, आदिमता के लिए।
- प्रोथ का प्रमेय (1878)। होने देना N = k 2m + 1 विषम के साथ k < 2m. यदि कोई पूर्णांक a ऐसा है कि
- तब प्रधान है। इसके विपरीत, यदि उपरोक्त समरूपता धारण नहीं करती है, और इसके अतिरिक्त
- (जैकोबी प्रतीक देखें)
- तब समग्र है।
अगर N = Fn > 3, तो उपरोक्त जैकोबी प्रतीक हमेशा -1 के बराबर होता है a = 3, और प्रोथ के प्रमेय के इस विशेष मामले को पेपिन के परीक्षण के रूप में जाना जाता है। हालांकि पेपिन के परीक्षण और प्रोथ के प्रमेय को कंप्यूटर पर कुछ फर्मैट संख्याओं की संमिश्रता साबित करने के लिए लागू किया गया है, न ही परीक्षण एक विशिष्ट गैर-तुच्छ कारक देता है। वास्तव में, कोई विशिष्ट प्रमुख कारक ज्ञात नहीं हैं n = 20 और 24.
गुणनखंड
फ़र्मेट संख्या के आकार के कारण, इसका गुणनखंडन करना या यहां तक कि मौलिकता की जांच करना भी मुश्किल है। पेपिन का परीक्षण फ़र्मेट नंबरों की प्राथमिकता के लिए एक आवश्यक और पर्याप्त स्थिति देता है, और आधुनिक कंप्यूटरों द्वारा इसे लागू किया जा सकता है। अण्डाकार वक्र विधि संख्याओं के छोटे अभाज्य भाजक खोजने की एक तेज़ विधि है। डिस्ट्रीब्यूटेड कंप्यूटिंग प्रोजेक्ट फर्मैटसर्च ने फर्मैट नंबरों के कुछ कारकों को पाया है। Yves Gallot's proth.exe का उपयोग बड़े Fermat नंबरों के कारकों को खोजने के लिए किया गया है। एडुआर्ड लुकास, यूलर के उपर्युक्त परिणाम में सुधार करते हुए, 1878 में साबित कर दिया कि फर्मेट संख्या का हर कारक , n के साथ कम से कम 2, रूप का है (प्रोथ संख्या देखें), जहाँ k एक धनात्मक पूर्णांक है। अपने आप में, यह ज्ञात फ़र्मेट प्राइम्स की मौलिकता को साबित करना आसान बनाता है।
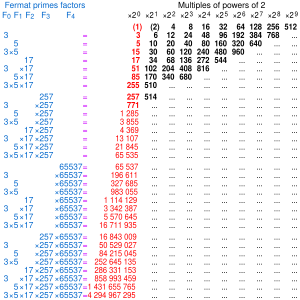
पहले बारह फर्मेट संख्याओं के गुणनखंड इस प्रकार हैं:
F0 = 21 + 1 = 3 is prime F1 = 22 + 1 = 5 is prime F2 = 24 + 1 = 17 is prime F3 = 28 + 1 = 257 is prime F4 = 216 + 1 = 65,537 is the largest known Fermat prime F5 = 232 + 1 = 4,294,967,297 = 641 × 6,700,417 (fully factored 1732[6]) F6 = 264 + 1 = 18,446,744,073,709,551,617 (20 digits) = 274,177 × 67,280,421,310,721 (14 digits) (fully factored 1855) F7 = 2128 + 1 = 340,282,366,920,938,463,463,374,607,431,768,211,457 (39 digits) = 59,649,589,127,497,217 (17 digits) × 5,704,689,200,685,129,054,721 (22 digits) (fully factored 1970) F8 = 2256 + 1 = 115,792,089,237,316,195,423,570,985,008,687,907,853,269,984,665,640,564,039,457,584,007,913,129,
639,937 (78 digits)= 1,238,926,361,552,897 (16 digits) ×
93,461,639,715,357,977,769,163,558,199,606,896,584,051,237,541,638,188,580,280,321 (62 digits) (fully factored 1980)F9 = 2512 + 1 = 13,407,807,929,942,597,099,574,024,998,205,846,127,479,365,820,592,393,377,723,561,443,721,764,0
30,073,546,976,801,874,298,166,903,427,690,031,858,186,486,050,853,753,882,811,946,569,946,433,6
49,006,084,097 (155 digits)= 2,424,833 × 7,455,602,825,647,884,208,337,395,736,200,454,918,783,366,342,657 (49 digits) ×
741,640,062,627,530,801,524,787,141,901,937,474,059,940,781,097,519,023,905,821,316,144,415,759,
504,705,008,092,818,711,693,940,737 (99 digits) (fully factored 1990)F10 = 21024 + 1 = 179,769,313,486,231,590,772,930...304,835,356,329,624,224,137,217 (309 digits) = 45,592,577 × 6,487,031,809 × 4,659,775,785,220,018,543,264,560,743,076,778,192,897 (40 digits) ×
130,439,874,405,488,189,727,484...806,217,820,753,127,014,424,577 (252 digits) (fully factored 1995)F11 = 22048 + 1 = 32,317,006,071,311,007,300,714,8...193,555,853,611,059,596,230,657 (617 digits) = 319,489 × 974,849 × 167,988,556,341,760,475,137 (21 digits) × 3,560,841,906,445,833,920,513 (22 digits) ×
173,462,447,179,147,555,430,258...491,382,441,723,306,598,834,177 (564 digits) (fully factored 1988)
As of November 2021[update], केवल एफ0 एफ के लिए11 पूरी तरह से पूर्णांक गुणनखंड किया गया है।[4]वितरित अभिकलन प्रोजेक्ट फ़र्मैट सर्च फ़र्मैट नंबरों के नए कारकों की खोज कर रहा है।[7] पूर्णांक अनुक्रमों के ऑन-लाइन विश्वकोश में सभी फर्मेट कारकों का सेट OEIS: A050922 (या, क्रमबद्ध, OEIS: A023394) है।
1950 से पहले फ़र्मेट संख्या के निम्नलिखित कारक ज्ञात थे (तब से, डिजिटल कंप्यूटरों ने और अधिक कारकों को खोजने में मदद की है):
| Year | Finder | Fermat number | Factor |
|---|---|---|---|
| 1732 | Euler | ||
| 1732 | Euler | (fully factored) | |
| 1855 | Clausen | ||
| 1855 | Clausen | (fully factored) | |
| 1877 | Pervushin | ||
| 1878 | Pervushin | ||
| 1886 | Seelhoff | ||
| 1899 | Cunningham | ||
| 1899 | Cunningham | ||
| 1903 | Western | ||
| 1903 | Western | ||
| 1903 | Western | ||
| 1903 | Western | ||
| 1903 | Cullen | ||
| 1906 | Morehead | ||
| 1925 | Kraitchik |
As of January 2021[update], Fermat संख्याओं के 356 अभाज्य गुणनखंड ज्ञात हैं, और 312 Fermat संख्याएँ सम्मिश्र कहलाती हैं।[4] हर साल कई नए फर्मेट कारक पाए जाते हैं।[8]
स्यूडोप्राइम्स और फर्मेट नंबर
फॉर्म 2 की मिश्रित संख्या की तरहp − 1, प्रत्येक मिश्रित फर्मेट संख्या आधार 2 के लिए एक मजबूत स्यूडोप्राइम है। इसका कारण यह है कि बेस 2 के लिए सभी मजबूत स्यूडोप्राइम भी फर्मेट स्यूडोप्राइम हैं - अर्थात,
सभी फर्मेट नंबरों के लिए।
1904 में, सिपोला ने दिखाया कि कम से कम दो अलग-अलग अभाज्य या समग्र फर्मेट संख्याओं का गुणनफल बेस 2 के लिए फ़र्मेट स्यूडोप्राइम होगा यदि और केवल यदि .[9]
फर्मेट संख्या के बारे में अन्य प्रमेय
Lemma. — If n is a positive integer,
Theorem — If is an odd prime, then is a power of 2.
If is a positive integer but not a power of 2, it must have an odd prime factor , and we may write where .
By the preceding lemma, for positive integer ,
where means "evenly divides". Substituting , and and using that is odd,
and thus
Because , it follows that is not prime. Therefore, by contraposition must be a power of 2.
Theorem — A Fermat prime cannot be a Wieferich prime.
We show if is a Fermat prime (and hence by the above, m is a power of 2), then the congruence does not hold.
Since we may write . If the given congruence holds, then , and therefore
Hence , and therefore . This leads to , which is impossible since .
Theorem (Édouard Lucas) — Any prime divisor p of is of the form whenever n > 1.
Let Gp denote the group of non-zero integers modulo p under multiplication, which has order p − 1. Notice that 2 (strictly speaking, its image modulo p) has multiplicative order equal to in Gp (since is the square of which is −1 modulo Fn), so that, by Lagrange's theorem, p − 1 is divisible by and p has the form for some integer k, as Euler knew. Édouard Lucas went further. Since n > 1, the prime p above is congruent to 1 modulo 8. Hence (as was known to Carl Friedrich Gauss), 2 is a quadratic residue modulo p, that is, there is integer a such that Then the image of a has order in the group Gp and (using Lagrange's theorem again), p − 1 is divisible by and p has the form for some integer s.
In fact, it can be seen directly that 2 is a quadratic residue modulo p, since
चूंकि 2 की विषम शक्ति एक द्विघात अवशेष सापेक्ष p है, इसलिए 2 ही है।
एक फ़र्मेट संख्या एक पूर्ण संख्या या सौहार्दपूर्ण संख्याओं की एक जोड़ी का हिस्सा नहीं हो सकती है। (Luca 2000) Fermat संख्याओं के सभी अभाज्य भाजकों के व्युत्क्रमों की श्रृंखला अभिसरण श्रृंखला है। (Křížek, Luca & Somer 2002) अगर nn + 1 अभाज्य है, वहाँ एक पूर्णांक m मौजूद है जैसे कि n = 22m. समीकरण nn + 1 = F(2m+m) उस मामले में रखता है।[10][11] बता दें कि Fermat संख्या F का सबसे बड़ा अभाज्य गुणक हैn पी (एफn). तब,
रचनात्मक बहुभुजों से संबंध
कार्ल फ्रेडरिक गॉस ने गॉसियन काल के सिद्धांत को अपने अंकगणितीय शोध में विकसित किया और नियमित बहुभुजों की निर्माण क्षमता के लिए पर्याप्त स्थिति तैयार की। गॉस ने कहा कि यह शर्त भी आवश्यक शर्त थी,[12] लेकिन कभी सबूत प्रकाशित नहीं किया। पियरे वांजेल ने 1837 में आवश्यकता का पूर्ण प्रमाण दिया। परिणाम को गॉस-वैंटजेल प्रमेय के रूप में जाना जाता है:
- एक n-पक्षीय नियमित बहुभुज का निर्माण कम्पास और स्ट्रेटेज के साथ किया जा सकता है यदि और केवल यदि n 2 की शक्ति का उत्पाद है और विशिष्ट Fermat primes: दूसरे शब्दों में, यदि और केवल यदि n फॉर्म का है n = 2kp1p2...ps, जहाँ k, s अऋणात्मक पूर्णांक हैं और pi विशिष्ट फर्मेट प्राइम्स हैं।
एक धनात्मक पूर्णांक n उपरोक्त रूप का है यदि और केवल यदि इसका यूलर का पूर्ण फलन φ(n) 2 की शक्ति है।
फ़र्मेट नंबरों के अनुप्रयोग
छद्म आयामी संख्या पीढ़ी
फर्मेट प्राइम विशेष रूप से 1, ..., एन, जहां एन 2 की शक्ति है, में संख्याओं के छद्म-यादृच्छिक अनुक्रम उत्पन्न करने में उपयोगी होते हैं। सबसे आम विधि का उपयोग 1 और के बीच किसी भी बीज मूल्य को लेने के लिए किया जाता है। P − 1, जहां पी फर्मेट प्राइम है। अब इसे एक संख्या A से गुणा करें, जो P के वर्गमूल से अधिक है और एक आदिम मूल modulo n modulo P है (अर्थात, यह द्विघात अवशेष नहीं है)। फिर परिणाम मोडुलो पी लें। परिणाम आरएनजी के लिए नया मान है।
- (रैखिक सर्वांगसम जनरेटर, RANDU देखें)
यह कंप्यूटर विज्ञान में उपयोगी है, क्योंकि अधिकांश डेटा संरचनाओं में 2 सदस्य होते हैंएक्स </सुप> संभावित मान। उदाहरण के लिए, एक बाइट में 256 (28) संभावित मान (0–255)। इसलिए, एक बाइट या बाइट्स को यादृच्छिक मानों से भरने के लिए, एक यादृच्छिक संख्या जनरेटर का उपयोग किया जा सकता है जो 1-256 मान उत्पन्न करता है, बाइट आउटपुट मान -1 लेता है। इस कारण से बहुत बड़े Fermat primes डेटा एन्क्रिप्शन में विशेष रुचि रखते हैं। यह विधि बाद में केवल छद्म यादृच्छिक मान उत्पन्न करती है P − 1 दोहराव, क्रम दोहराता है। खराब तरीके से चुने गए गुणक के परिणामस्वरूप क्रम जल्दी ही दोहराया जा सकता है P − 1.
सामान्यीकृत फर्मेट संख्या
फॉर्म के नंबर a, b के साथ कोई सह अभाज्य पूर्णांक, a > b > 0, सामान्यीकृत फर्मेट संख्याएं कहलाती हैं। एक विषम अभाज्य p एक सामान्यीकृत फर्मेट संख्या है यदि और केवल यदि p पायथागॉरियन प्राइम के अनुरूप है। 1 (mod 4)। (यहाँ हम केवल मामले पर विचार करते हैं n > 0, इसलिए 3 = कोई प्रति उदाहरण नहीं है।)
इस फॉर्म के संभावित प्राइम का एक उदाहरण 1215 है131072 + 242131072 (केलेन शेंटन द्वारा पाया गया)।[13] साधारण फ़र्मेट संख्याओं के अनुरूप, प्रपत्र के सामान्यीकृत फ़र्मैट नंबरों को लिखना आम है एफ के रूप मेंn(ए)। इस अंकन में, उदाहरण के लिए, संख्या 100,000,001 को F के रूप में लिखा जाएगा3(10)। निम्नलिखित में हम स्वयं को इस रूप की अभाज्य संख्याओं तक सीमित रखेंगे, , ऐसे अभाज्य को फर्मेट अभाज्य आधार a कहा जाता है। बेशक, ये अभाज्य संख्याएँ केवल तभी मौजूद होती हैं जब a समता (गणित) हो।
अगर हमें चाहिए n > 0, फिर लन्दौ की समस्याएँ | लन्दौ की चौथी समस्या पूछती है कि क्या अपरिमित रूप से कई सामान्यीकृत फ़र्मैट अभाज्य F हैंn(ए)।
सामान्यीकृत फर्मेट प्राइम्स
उनकी मौलिकता को साबित करने में आसानी के कारण, हाल के वर्षों में सामान्यीकृत फ़र्मेट प्राइम संख्या सिद्धांत के क्षेत्र में शोध का विषय बन गए हैं। आज के सबसे बड़े ज्ञात अभाज्यों में से कई सामान्यीकृत फर्मेट अभाज्य हैं।
सामान्यीकृत Fermat संख्याएँ केवल सम के लिए ही अभाज्य हो सकती हैं a, क्योंकि अगर a विषम है तो प्रत्येक सामान्यीकृत फर्मेट संख्या 2 से विभाज्य होगी। सबसे छोटी अभाज्य संख्या साथ है , या 3032 + 1. इसके अलावा, हम एक विषम आधार के लिए आधे सामान्यीकृत फर्मेट संख्या को परिभाषित कर सकते हैं, एक आधार के लिए एक आधा सामान्यीकृत फर्मेट संख्या (विषम के लिए) है , और यह भी उम्मीद की जानी चाहिए कि प्रत्येक विषम आधार के लिए केवल कई आधे सामान्यीकृत फर्मेट प्राइम होंगे।
(सूची में सामान्यीकृत फर्मेट संख्याएं () एक सम तक a हैं , विषम के लिए a, वे हैं . अगर a विषम घातांक वाली एक पूर्ण शक्ति है (sequence A070265 in the OEIS), तब सभी सामान्यीकृत फर्मेट संख्या बीजगणितीय कारक हो सकते हैं, इसलिए वे अभाज्य नहीं हो सकते हैं)
(सबसे छोटी संख्या के लिए ऐसा है कि प्रधान है, देखिए OEIS: A253242)
| numbers such that is prime |
numbers such that is prime |
numbers such that is prime |
numbers such that is prime | ||||
|---|---|---|---|---|---|---|---|
| 2 | 0, 1, 2, 3, 4, ... | 18 | 0, ... | 34 | 2, ... | 50 | ... |
| 3 | 0, 1, 2, 4, 5, 6, ... | 19 | 1, ... | 35 | 1, 2, 6, ... | 51 | 1, 3, 6, ... |
| 4 | 0, 1, 2, 3, ... | 20 | 1, 2, ... | 36 | 0, 1, ... | 52 | 0, ... |
| 5 | 0, 1, 2, ... | 21 | 0, 2, 5, ... | 37 | 0, ... | 53 | 3, ... |
| 6 | 0, 1, 2, ... | 22 | 0, ... | 38 | ... | 54 | 1, 2, 5, ... |
| 7 | 2, ... | 23 | 2, ... | 39 | 1, 2, ... | 55 | ... |
| 8 | (none) | 24 | 1, 2, ... | 40 | 0, 1, ... | 56 | 1, 2, ... |
| 9 | 0, 1, 3, 4, 5, ... | 25 | 0, 1, ... | 41 | 4, ... | 57 | 0, 2, ... |
| 10 | 0, 1, ... | 26 | 1, ... | 42 | 0, ... | 58 | 0, ... |
| 11 | 1, 2, ... | 27 | (none) | 43 | 3, ... | 59 | 1, ... |
| 12 | 0, ... | 28 | 0, 2, ... | 44 | 4, ... | 60 | 0, ... |
| 13 | 0, 2, 3, ... | 29 | 1, 2, 4, ... | 45 | 0, 1, ... | 61 | 0, 1, 2, ... |
| 14 | 1, ... | 30 | 0, 5, ... | 46 | 0, 2, 9, ... | 62 | ... |
| 15 | 1, ... | 31 | ... | 47 | 3, ... | 63 | ... |
| 16 | 0, 1, 2, ... | 32 | (none) | 48 | 2, ... | 64 | (none) |
| 17 | 2, ... | 33 | 0, 3, ... | 49 | 1, ... | 65 | 1, 2, 5, ... |
| b | known generalized (half) Fermat prime base b |
| 2 | 3, 5, 17, 257, 65537 |
| 3 | 2, 5, 41, 21523361, 926510094425921, 1716841910146256242328924544641 |
| 4 | 5, 17, 257, 65537 |
| 5 | 3, 13, 313 |
| 6 | 7, 37, 1297 |
| 7 | 1201 |
| 8 | (not possible) |
| 9 | 5, 41, 21523361, 926510094425921, 1716841910146256242328924544641 |
| 10 | 11, 101 |
| 11 | 61, 7321 |
| 12 | 13 |
| 13 | 7, 14281, 407865361 |
| 14 | 197 |
| 15 | 113 |
| 16 | 17, 257, 65537 |
| 17 | 41761 |
| 18 | 19 |
| 19 | 181 |
| 20 | 401, 160001 |
| 21 | 11, 97241, 1023263388750334684164671319051311082339521 |
| 22 | 23 |
| 23 | 139921 |
| 24 | 577, 331777 |
| 25 | 13, 313 |
| 26 | 677 |
| 27 | (not possible) |
| 28 | 29, 614657 |
| 29 | 421, 353641, 125123236840173674393761 |
| 30 | 31, 185302018885184100000000000000000000000000000001 |
| 31 | |
| 32 | (not possible) |
| 33 | 17, 703204309121 |
| 34 | 1336337 |
| 35 | 613, 750313, 330616742651687834074918381127337110499579842147487712949050636668246738736343104392290115356445313 |
| 36 | 37, 1297 |
| 37 | 19 |
| 38 | |
| 39 | 761, 1156721 |
| 40 | 41, 1601 |
| 41 | 31879515457326527173216321 |
| 42 | 43 |
| 43 | 5844100138801 |
| 44 | 197352587024076973231046657 |
| 45 | 23, 1013 |
| 46 | 47, 4477457, 46512+1 (852 digits: 214787904487...289480994817) |
| 47 | 11905643330881 |
| 48 | 5308417 |
| 49 | 1201 |
| 50 |
(देखना [14][15] अधिक जानकारी के लिए (यहां तक कि 1000 तक के आधार), यह भी देखें [16] विषम आधारों के लिए)
(फॉर्म के सबसे छोटे प्राइम के लिए (विषम के लिए ), यह सभी देखें OEIS: A111635)
| numbers such that is prime | ||
|---|---|---|
| 2 | 1 | 0, 1, 2, 3, 4, ... |
| 3 | 1 | 0, 1, 2, 4, 5, 6, ... |
| 3 | 2 | 0, 1, 2, ... |
| 4 | 1 | 0, 1, 2, 3, ... |
| 4 | 3 | 0, 2, 4, ... |
| 5 | 1 | 0, 1, 2, ... |
| 5 | 2 | 0, 1, 2, ... |
| 5 | 3 | 1, 2, 3, ... |
| 5 | 4 | 1, 2, ... |
| 6 | 1 | 0, 1, 2, ... |
| 6 | 5 | 0, 1, 3, 4, ... |
| 7 | 1 | 2, ... |
| 7 | 2 | 1, 2, ... |
| 7 | 3 | 0, 1, 8, ... |
| 7 | 4 | 0, 2, ... |
| 7 | 5 | 1, 4, ... |
| 7 | 6 | 0, 2, 4, ... |
| 8 | 1 | (none) |
| 8 | 3 | 0, 1, 2, ... |
| 8 | 5 | 0, 1, 2, ... |
| 8 | 7 | 1, 4, ... |
| 9 | 1 | 0, 1, 3, 4, 5, ... |
| 9 | 2 | 0, 2, ... |
| 9 | 4 | 0, 1, ... |
| 9 | 5 | 0, 1, 2, ... |
| 9 | 7 | 2, ... |
| 9 | 8 | 0, 2, 5, ... |
| 10 | 1 | 0, 1, ... |
| 10 | 3 | 0, 1, 3, ... |
| 10 | 7 | 0, 1, 2, ... |
| 10 | 9 | 0, 1, 2, ... |
| 11 | 1 | 1, 2, ... |
| 11 | 2 | 0, 2, ... |
| 11 | 3 | 0, 3, ... |
| 11 | 4 | 1, 2, ... |
| 11 | 5 | 1, ... |
| 11 | 6 | 0, 1, 2, ... |
| 11 | 7 | 2, 4, 5, ... |
| 11 | 8 | 0, 6, ... |
| 11 | 9 | 1, 2, ... |
| 11 | 10 | 5, ... |
| 12 | 1 | 0, ... |
| 12 | 5 | 0, 4, ... |
| 12 | 7 | 0, 1, 3, ... |
| 12 | 11 | 0, ... |
| 13 | 1 | 0, 2, 3, ... |
| 13 | 2 | 1, 3, 9, ... |
| 13 | 3 | 1, 2, ... |
| 13 | 4 | 0, 2, ... |
| 13 | 5 | 1, 2, 4, ... |
| 13 | 6 | 0, 6, ... |
| 13 | 7 | 1, ... |
| 13 | 8 | 1, 3, 4, ... |
| 13 | 9 | 0, 3, ... |
| 13 | 10 | 0, 1, 2, 4, ... |
| 13 | 11 | 2, ... |
| 13 | 12 | 1, 2, 5, ... |
| 14 | 1 | 1, ... |
| 14 | 3 | 0, 3, ... |
| 14 | 5 | 0, 2, 4, 8, ... |
| 14 | 9 | 0, 1, 8, ... |
| 14 | 11 | 1, ... |
| 14 | 13 | 2, ... |
| 15 | 1 | 1, ... |
| 15 | 2 | 0, 1, ... |
| 15 | 4 | 0, 1, ... |
| 15 | 7 | 0, 1, 2, ... |
| 15 | 8 | 0, 2, 3, ... |
| 15 | 11 | 0, 1, 2, ... |
| 15 | 13 | 1, 4, ... |
| 15 | 14 | 0, 1, 2, 4, ... |
| 16 | 1 | 0, 1, 2, ... |
| 16 | 3 | 0, 2, 8, ... |
| 16 | 5 | 1, 2, ... |
| 16 | 7 | 0, 6, ... |
| 16 | 9 | 1, 3, ... |
| 16 | 11 | 2, 4, ... |
| 16 | 13 | 0, 3, ... |
| 16 | 15 | 0, ... |
(सबसे छोटे आधार के लिए भी a ऐसा है कि प्रधान है, देखिए OEIS: A056993)
| bases a such that is prime (only consider even a) | OEIS sequence | |
|---|---|---|
| 0 | 2, 4, 6, 10, 12, 16, 18, 22, 28, 30, 36, 40, 42, 46, 52, 58, 60, 66, 70, 72, 78, 82, 88, 96, 100, 102, 106, 108, 112, 126, 130, 136, 138, 148, 150, ... | A006093 |
| 1 | 2, 4, 6, 10, 14, 16, 20, 24, 26, 36, 40, 54, 56, 66, 74, 84, 90, 94, 110, 116, 120, 124, 126, 130, 134, 146, 150, 156, 160, 170, 176, 180, 184, ... | A005574 |
| 2 | 2, 4, 6, 16, 20, 24, 28, 34, 46, 48, 54, 56, 74, 80, 82, 88, 90, 106, 118, 132, 140, 142, 154, 160, 164, 174, 180, 194, 198, 204, 210, 220, 228, ... | A000068 |
| 3 | 2, 4, 118, 132, 140, 152, 208, 240, 242, 288, 290, 306, 378, 392, 426, 434, 442, 508, 510, 540, 542, 562, 596, 610, 664, 680, 682, 732, 782, ... | A006314 |
| 4 | 2, 44, 74, 76, 94, 156, 158, 176, 188, 198, 248, 288, 306, 318, 330, 348, 370, 382, 396, 452, 456, 470, 474, 476, 478, 560, 568, 598, 642, ... | A006313 |
| 5 | 30, 54, 96, 112, 114, 132, 156, 332, 342, 360, 376, 428, 430, 432, 448, 562, 588, 726, 738, 804, 850, 884, 1068, 1142, 1198, 1306, 1540, 1568, ... | A006315 |
| 6 | 102, 162, 274, 300, 412, 562, 592, 728, 1084, 1094, 1108, 1120, 1200, 1558, 1566, 1630, 1804, 1876, 2094, 2162, 2164, 2238, 2336, 2388, ... | A006316 |
| 7 | 120, 190, 234, 506, 532, 548, 960, 1738, 1786, 2884, 3000, 3420, 3476, 3658, 4258, 5788, 6080, 6562, 6750, 7692, 8296, 9108, 9356, 9582, ... | A056994 |
| 8 | 278, 614, 892, 898, 1348, 1494, 1574, 1938, 2116, 2122, 2278, 2762, 3434, 4094, 4204, 4728, 5712, 5744, 6066, 6508, 6930, 7022, 7332, ... | A056995 |
| 9 | 46, 1036, 1318, 1342, 2472, 2926, 3154, 3878, 4386, 4464, 4474, 4482, 4616, 4688, 5374, 5698, 5716, 5770, 6268, 6386, 6682, 7388, 7992, ... | A057465 |
| 10 | 824, 1476, 1632, 2462, 2484, 2520, 3064, 3402, 3820, 4026, 6640, 7026, 7158, 9070, 12202, 12548, 12994, 13042, 15358, 17646, 17670, ... | A057002 |
| 11 | 150, 2558, 4650, 4772, 11272, 13236, 15048, 23302, 26946, 29504, 31614, 33308, 35054, 36702, 37062, 39020, 39056, 43738, 44174, 45654, ... | A088361 |
| 12 | 1534, 7316, 17582, 18224, 28234, 34954, 41336, 48824, 51558, 51914, 57394, 61686, 62060, 89762, 96632, 98242, 100540, 101578, 109696, ... | A088362 |
| 13 | 30406, 71852, 85654, 111850, 126308, 134492, 144642, 147942, 150152, 165894, 176206, 180924, 201170, 212724, 222764, 225174, 241600, ... | A226528 |
| 14 | 67234, 101830, 114024, 133858, 162192, 165306, 210714, 216968, 229310, 232798, 422666, 426690, 449732, 462470, 468144, 498904, 506664, ... | A226529 |
| 15 | 70906, 167176, 204462, 249830, 321164, 330716, 332554, 429370, 499310, 524552, 553602, 743788, 825324, 831648, 855124, 999236, 1041870, ... | A226530 |
| 16 | 48594, 108368, 141146, 189590, 255694, 291726, 292550, 357868, 440846, 544118, 549868, 671600, 843832, 857678, 1024390, 1057476, 1087540, ... | A251597 |
| 17 | 62722, 130816, 228188, 386892, 572186, 689186, 909548, 1063730, 1176694, 1361244, 1372930, 1560730, 1660830, 1717162, 1722230, 1766192, ... | A253854 |
| 18 | 24518, 40734, 145310, 361658, 525094, 676754, 773620, 1415198, 1488256, 1615588, 1828858, 2042774, 2514168, 2611294, 2676404, 3060772, ... | A244150 |
| 19 | 75898, 341112, 356926, 475856, 1880370, 2061748, 2312092, 2733014, 2788032, 2877652, 2985036, 3214654, 3638450, 4896418, 5897794, ... | A243959 |
| 20 | 919444, 1059094, 1951734, 1963736, ... | A321323 |
सबसे छोटा आधार b ऐसा है कि b2n + 1 अभाज्य हैं
- 2, 2, 2, 2, 2, 30, 102, 120, 278, 46, 824, 150, 1534, 30406, 67234, 70906, 48594, 62722, 24518, 75898, 919444, ... (sequence A056993 in the OEIS)
सबसे छोटा k ऐसा है कि (2n)k + 1 अभाज्य हैं
- 1, 1, 1, 0, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 0, 4, 1, ... (अगला पद अज्ञात है) (sequence A079706 in the OEIS) (यह भी देखें OEIS: A228101 और OEIS: A084712)
जिसके लिए आधारों की संख्या की भविष्यवाणी करने के लिए एक अधिक विस्तृत सिद्धांत का उपयोग किया जा सकता है फिक्स्ड के लिए प्राइम होगा . सामान्यीकृत Fermat primes की संख्या लगभग आधी होने की उम्मीद की जा सकती है 1 से बढ़ा है।
सबसे बड़ा ज्ञात सामान्यीकृत फर्मेट प्राइम्स
निम्नलिखित 5 सबसे बड़े ज्ञात सामान्यीकृत फर्मेट प्राइम्स की सूची है।[17] पूरे शीर्ष-5 की खोज प्राइमग्रिड परियोजना के प्रतिभागियों द्वारा की गई है।
| Rank | Prime number | Generalized Fermat notation | Number of digits | Discovery date | ref. |
|---|---|---|---|---|---|
| 1 | 19637361048576 + 1 | F20(1963736) | 6,598,776 | Sep 2022 | [18] |
| 2 | 19517341048576 + 1 | F20(1951734) | 6,595,985 | Aug 2022 | [19] |
| 3 | 10590941048576 + 1 | F20(1059094) | 6,317,602 | Nov 2018 | [20] |
| 4 | 9194441048576 + 1 | F20(919444) | 6,253,210 | Sep 2017 | [21] |
| 5 | 25 × 213719266 + 1 | F1(5 × 26859633) | 4,129,912 | Sep 2022 | [22] |
प्रधान पन्ने पर कोई भी वर्तमान शीर्ष 100 सामान्यीकृत Fermat primes पा सकता है।
यह भी देखें
- रचनात्मक बहुभुज: कौन से नियमित बहुभुज आंशिक रूप से निर्माण योग्य हैं, यह फर्मेट प्राइम्स पर निर्भर करता है।
- दोहरा घातीय कार्य
- लुकास प्रमेय
- मेर्सन प्रीमियम
- पियरपोंट प्राइम
- प्रधानता परीक्षण
- प्रोथ का प्रमेय
- स्यूडोप्राइम
- सीरपिन्स्की संख्या
- सिल्वेस्टर का क्रम
टिप्पणियाँ
- ↑ Křížek, Luca & Somer 2001, p. 38, Remark 4.15
- ↑ Chris Caldwell, "Prime Links++: special forms" Archived 2013-12-24 at the Wayback Machine at The Prime Pages.
- ↑ Ribenboim 1996, p. 88.
- ↑ 4.0 4.1 4.2 Keller, Wilfrid (January 18, 2021), "Prime Factors of Fermat Numbers", ProthSearch.com, retrieved January 19, 2021
- ↑ Boklan, Kent D.; Conway, John H. (2017). "Expect at most one billionth of a new Fermat Prime!". The Mathematical Intelligencer. 39 (1): 3–5. arXiv:1605.01371. doi:10.1007/s00283-016-9644-3. S2CID 119165671.
- ↑ Sandifer, Ed. "How Euler Did it" (PDF). MAA Online. Mathematical Association of America. Archived (PDF) from the original on 2022-10-09. Retrieved 2020-06-13.
- ↑ ":: F E R M A T S E A R C H . O R G :: Home page". www.fermatsearch.org. Retrieved 7 April 2018.
- ↑ "::FERMATSEARCH.ORG:: News". www.fermatsearch.org. Retrieved 7 April 2018.
- ↑ Krizek, Michal; Luca, Florian; Somer, Lawrence (14 March 2013). 17 Lectures on Fermat Numbers: From Number Theory to Geometry. Springer Science & Business Media. ISBN 9780387218502. Retrieved 7 April 2018 – via Google Books.
- ↑ Jeppe Stig Nielsen, "S(n) = n^n + 1".
- ↑ Weisstein, Eric W. "Sierpiński Number of the First Kind". MathWorld.
- ↑ Gauss, Carl Friedrich (1966). Disquisitiones arithmeticae. New Haven and London: Yale University Press. pp. 458–460. Retrieved 25 January 2023.
- ↑ PRP Top Records, search for x^131072+y^131072, by Henri & Renaud Lifchitz.
- ↑ "Generalized Fermat Primes". jeppesn.dk. Retrieved 7 April 2018.
- ↑ "Generalized Fermat primes for bases up to 1030". noprimeleftbehind.net. Retrieved 7 April 2018.
- ↑ "Generalized Fermat primes in odd bases". fermatquotient.com. Retrieved 7 April 2018.
- ↑ Caldwell, Chris K. "The Top Twenty: Generalized Fermat". The Prime Pages. Retrieved 11 July 2019.
- ↑ 19637361048576 + 1
- ↑ 19517341048576 + 1
- ↑ 10590941048576 + 1
- ↑ 9194441048576 + 1
- ↑ 25*213719266 + 1
संदर्भ
- Golomb, S. W. (January 1, 1963), "On the sum of the reciprocals of the Fermat numbers and related irrationalities", Canadian Journal of Mathematics, 15: 475–478, doi:10.4153/CJM-1963-051-0, S2CID 123138118
- Grytczuk, A.; Luca, F. & Wójtowicz, M. (2001), "Another note on the greatest prime factors of Fermat numbers", Southeast Asian Bulletin of Mathematics, 25 (1): 111–115, doi:10.1007/s10012-001-0111-4, S2CID 122332537
- Guy, Richard K. (2004), Unsolved Problems in Number Theory, Problem Books in Mathematics, vol. 1 (3rd ed.), New York: Springer Verlag, pp. A3, A12, B21, ISBN 978-0-387-20860-2
- Křížek, Michal; Luca, Florian & Somer, Lawrence (2001), 17 Lectures on Fermat Numbers: From Number Theory to Geometry, CMS books in mathematics, vol. 10, New York: Springer, ISBN 978-0-387-95332-8 - This book contains an extensive list of references.
- Křížek, Michal; Luca, Florian & Somer, Lawrence (2002), "On the convergence of series of reciprocals of primes related to the Fermat numbers", Journal of Number Theory, 97 (1): 95–112, doi:10.1006/jnth.2002.2782
- Luca, Florian (2000), "The anti-social Fermat number", American Mathematical Monthly, 107 (2): 171–173, doi:10.2307/2589441, JSTOR 2589441
- Ribenboim, Paulo (1996), The New Book of Prime Number Records (3rd ed.), New York: Springer, ISBN 978-0-387-94457-9
- Robinson, Raphael M. (1954), "Mersenne and Fermat Numbers", Proceedings of the American Mathematical Society, 5 (5): 842–846, doi:10.2307/2031878, JSTOR 2031878
- Yabuta, M. (2001), "A simple proof of Carmichael's theorem on primitive divisors" (PDF), Fibonacci Quarterly, 39: 439–443, archived (PDF) from the original on 2022-10-09
बाहरी संबंध
- Chris Caldwell, The Prime Glossary: Fermat number at The Prime Pages.
- Luigi Morelli, History of Fermat Numbers
- John Cosgrave, Unification of Mersenne and Fermat Numbers
- Wilfrid Keller, Prime Factors of Fermat Numbers
- Weisstein, Eric W. "Fermat Number". MathWorld.
- Weisstein, Eric W. "Fermat Prime". MathWorld.
- Weisstein, Eric W. "Generalized Fermat Number". MathWorld.
- Yves Gallot, Generalized Fermat Prime Search
- Mark S. Manasse, Complete factorization of the ninth Fermat number (original announcement)
- Peyton Hayslette, Largest Known Generalized Fermat Prime Announcement
- Templates that generate short descriptions
- Articles containing potentially dated statements from 2023
- Articles containing potentially dated statements from 2014
- Articles containing potentially dated statements from November 2021
- Articles containing potentially dated statements from January 2021
- Collapse templates
- Navigational boxes
- Navigational boxes without horizontal lists
- Sidebars with styles needing conversion
- Templates generating microformats
- Templates that are not mobile friendly
- Wikipedia metatemplates
- Mathematics navigational boxes
- Templates Translated in Hindi
- Navbox orphans
- बिल्ड करने योग्य बहुभुज
- प्रमाण युक्त लेख
- संख्या सिद्धांत विषयक अनसुलझी समस्याएं
- बड़े पूर्णांक
- अभाज्य संख्याओं की कक्षाएं
- पूर्णांक अनुक्रम
- Machine Translated Page
- Created On 13/02/2023