मध्यवर्ती मूल्य प्रमेय
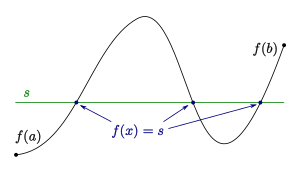
गणितीय विश्लेषण में, मध्यवर्ती मूल्य प्रमेय बताता है कि यदि सतत फलन (गणित) है जिसके फलन के क्षेत्र में अंतराल (गणित) [a, b] होता है , तो यह अंतराल के अन्दर किसी बिंदु पर और के बीच किसी भी दिए गए मान को लेता है।
इसके दो महत्वपूर्ण परिणाम हैं:
- यदि निरंतर फलन में अंतराल के अंदर विपरीत चिह्न के मान होते हैं, जिससे उस अंतराल (बोल्जानो के प्रमेय) में फलन शून्य होता है।[1] [2]
- एक अंतराल पर सतत फलन की इमेज (गणित) स्वयं अंतराल है।
प्रेरणा
यह वास्तविक संख्या पर निरंतर फलनों की एक सहज प्रोपर्टी को पकड़ता है: ज्ञात मूल्यों और , के साथ पर निरंतर दिया गया है और, तो का ग्राफ क्षैतिज रेखा से होकर निकलना चाहिए, जबकि से पर जाता है। यह इस विचार का प्रतिनिधित्व करता है कि एक बंद अंतराल पर एक सतत फलन का ग्राफ हो सकता है कागज से पेंसिल उठाए बिना खींचा गया था।
प्रमेय
मध्यवर्ती मूल्य प्रमेय निम्नलिखित बताता है:
एक अंतराल पर विचार करें वास्तविक संख्याओं और सतत फलन है . तब
- संस्करण I. यदि के बीच की संख्या और है, तो वहाँ है ऐसा है कि .
- संस्करण द्वितीय। फलन की इमेज अंतराल भी है, और इसमें सम्मिलित है ,
टिप्पणी: संस्करण II बताता है कि फलन मानों के समुच्चय (गणित) में कोई अंतर नहीं है। किसी भी दो फलन मानों के लिए , तथापि वे बीच और के अंतराल से बाहर हों, अंतराल में सभी बिंदु फलन मान भी हैं,
पूर्णता से संबंध
प्रमेय निर्भर करता है, और वास्तविक संख्याओं की पूर्णता के सामान्य है। मध्यवर्ती मूल्य प्रमेय परिमेय संख्या Q पर प्रयुक्त नहीं होता है क्योंकि परिमेय संख्याओं के बीच अंतराल उपस्थित होता है; अपरिमेय संख्याएँ उन अंतरालों को भरती हैं। उदाहरण के लिए, फलन के लिए संतुष्ट और . चूँकि, कोई परिमेय संख्या नहीं है ऐसा है कि , क्योंकि अपरिमेय संख्या है।
प्रमाण
प्रमेय को वास्तविक संख्याओं की पूर्णता (आदेश सिद्धांत) प्रोपर्टी के परिणाम के रूप में सिद्ध किया जा सकता है:[3] हम पहला स्थिति सिद्ध करेंगे, . दूसरा स्थिति भी ऐसा ही है।
माना सभी का समुच्चय हो ऐसा है कि . तब से खाली नहीं है का तत्व है . तब से खाली नहीं है और ऊपर से घिरा हुआ है , पूर्णता से, सर्वोच्चता उपस्थित है, सबसे छोटी संख्या है जो प्रत्येक सदस्य से अधिक या उसके सामान्य है . हम यह प्रमाणित करते हैं .
कुछ समुच्चय . है तब से निरंतर है, ऐसा है कि जब कभी भी . इस का कारण है कि
टिप्पणी: मध्यवर्ती मूल्य प्रमेय को गैर-मानक विश्लेषण के विधियों का उपयोग करके भी सिद्ध किया जा सकता है, जो कठोर पर अन्तर्ज्ञानी तर्कों को सम्मिलित करता है। [4]
इतिहास
प्रमेय का रूप 5 वीं शताब्दी ईसा पूर्व के रूप में पोस्ट किया गया था, ब्रायसन ऑफ हेराक्लिआ के काम में सर्कल को स्क्वायर करने पर ब्रायसन ने तर्क दिया कि, चूंकि दिए गए वर्ग से बड़े और छोटे दोनों वृत्त उपस्थित हैं, इसलिए सामान्य क्षेत्रफल का वृत्त उपस्थित होना चाहिए।[5] प्रमेय को पहली बार 1817 में बर्नार्ड बोलजानो द्वारा सिद्ध किया गया था। बोलजानो ने प्रमेय के निम्नलिखित सूत्रीकरण का उपयोग किया था:[6]
माना बीच के अंतराल और पर निरंतर फलन करें ऐसा है कि और . फिर है बीच में और ऐसा है कि .
इस सूत्र और आधुनिक सूत्र के बीच समानता को उचित निरंतर फलन के लिए समुच्चयिंग द्वारा दिखाया जा सकता है। ऑगस्टिन-लुई कॉची ने 1821 में आधुनिक सूत्रीकरण और प्रमाण प्रदान किया था।[7] दोनों फलनों के विश्लेषण को औपचारिक रूप देने के लक्ष्य और जोसेफ-लुई लाग्रेंज के काम से प्रेरित थे। यह विचार कि निरंतर फलनों में मध्यवर्ती मूल्य प्रोपर्टी होती है, पहले की उत्पत्ति होती है। साइमन स्टीवन ने समाधान के दशमलव विस्तार के निर्माण के लिए एल्गोरिदम प्रदान करके बहुपद के लिए मध्यवर्ती मूल्य प्रमेय (उदाहरण के रूप में घन फलन का उपयोग करके) सिद्ध कर दिया था। एल्गोरिथ्म पुनरावृत्ति के प्रत्येक चरण पर अतिरिक्त दशमलव अंक का निर्माण करते हुए, अंतराल को 10 भागों में उप-विभाजित करता है।[8] निरंतरता की औपचारिक परिभाषा दिए जाने से पहले, सतत फलन की परिभाषा के भाग के रूप में मध्यवर्ती मूल्य प्रोपर्टी दी गई थी। समर्थकों में लुई आर्बोगैस्ट सम्मिलित हैं, जिन्होंने माना कि फलनों में कोई छलांग नहीं है, मध्यवर्ती मूल्य प्रोपर्टी को संतुष्ट करते हैं और वेतन वृद्धि करते हैं जिनके आकार चर के वेतन वृद्धि के आकार के अनुरूप होते हैं।[9]
पहले के लेखकों ने परिणाम को सहज रूप से स्पष्ट माना और किसी प्रमाण की आवश्यकता नहीं थी। बोलजानो और कॉची की अंतर्दृष्टि निरंतरता की सामान्य धारणा को परिभाषित करना था (कॉची के स्थिति के संदर्भ में और बोलजानो के स्थिति में वास्तविक असमानताओं का उपयोग करना), और ऐसी परिभाषाओं के आधार पर प्रमाण प्रदान करना था।
सामान्यीकरण
इंटरमीडिएट वैल्यू प्रमेय टोपोलॉजी की टोपोलॉजी धारणा से निकटता से संयुक्तता है और मीट्रिक रिक्त स्थान में जुड़े समुच्चयों के मूल गुणों और विशेष रूप से आर के जुड़े सबसमुच्चय से निम्नानुसार है:
- यदि और मीट्रिक रिक्त स्थान हैं, सतत मैप है, और कनेक्टेड स्पेस सबसमुच्चय है, फिर जुड़ा है।
- उपसमुच्चय संयुक्तता है यदि और केवल यदि यह निम्नलिखित प्रोपर्टी को संतुष्ट करता है:
वास्तव में, संयुक्तता सांस्थितिक गुण है और (*) स्थलाकृतिक स्थानों के लिए सामान्यीकरण करता है: यदि और टोपोलॉजिकल स्पेस हैं, सतत मैप है, और कनेक्टेड स्पेस है, फिर जुड़ा है। निरंतर मैप के अनुसार संयुक्तता के संरक्षण को मध्यवर्ती मूल्य प्रमेय के सामान्यीकरण के रूप में माना जा सकता है, वास्तविक चर के वास्तविक मूल्यवान फलनों की प्रोपर्टी, सामान्य रिक्त स्थान में निरंतर फलनों के लिए
पहले बताए गए मध्यवर्ती मूल्य प्रमेय के पहले संस्करण को याद करें:
मध्यवर्ती मूल्य प्रमेय (संस्करण I) — किसी बंद अंतराल पर विचार करें वास्तविक संख्या में और एक सतत कार्य . तब, यदि ऐसी एक वास्तविक संख्या है , वहां अस्तित्व है such that .
मध्यवर्ती मूल्य प्रमेय संयुक्तता के इन दो गुणों का तत्काल परिणाम है:[10]
By (**), एक कनेक्टेड सेट है. (*) से यह पता चलता है कि छवि, , भी जुड़ा हुआ है. सुविधा के लिए मान लीजिये . फिर एक बार और आह्वान करें (**), implies that , or for some . इसलिए , वास्तव में कायम रहना चाहिए, और वांछित निष्कर्ष अनुसरण करता है. यही तर्क प्रयुक्त होता है यदि , तो हमारा कार्य हो गया. Q.E.D.
मध्यवर्ती मूल्य प्रमेय प्राकृतिक विधि से सामान्यीकरण करता है: मान लीजिए कि X कनेक्टेड टोपोलॉजिकल स्पेस है और (Y, <) आदेश टोपोलॉजी से लैस कुल ऑर्डर समुच्चय है, और माना f : X → Y सतत मानचित्र बनें। यदि a और b में दो बिन्दु हैं X और u में बिंदु है Y बीच पड़ा हुआ f(a) और f(b) इसके संबंध में <, तो वहाँ उपस्थित है c में X ऐसा है कि f(c) = u. मूल प्रमेय को नोट करके पुनर्प्राप्त किया जाता है इस प्रकार R संयुक्तता है और इसका प्राकृतिक टोपोलॉजिकल स्पेस ऑर्डर टोपोलॉजी है।
ब्रौवर निश्चित-बिंदु प्रमेय संबंधित प्रमेय है, जो आयाम में, मध्यवर्ती मान प्रमेय का विशेष स्थिति देता है।
विपरीत कृत्रिम
एक डार्बौक्स फलन वास्तविक-मूल्यवान फलन है जिसमें मध्यवर्ती f मूल्य गुण है, अर्थात, जो मध्यवर्ती मूल्य प्रमेय के निष्कर्ष को संतुष्ट करता है: किसी भी दो मूल्यों के लिए a और b के अधिकार क्षेत्र में f, और कोई भी y बीच में f(a) और f(b) है वहाँ कुछ c बीच में a और b साथ f(c) = y. मध्यवर्ती मूल्य प्रमेय कहता है कि प्रत्येक निरंतर फलन डार्बौक्स फलन है। चूँकि, प्रत्येक डार्बौक्स फलन निरंतर नहीं है; अर्थात्, मध्यवर्ती मान प्रमेय का विलोम असत्य है।
उदाहरण के अनुसार फलन को f : [0, ∞) → [−1, 1] द्वारा परिभाषित f(x) = sin(1/x) के लिए x > 0 और f(0) = 0. यह फलन निरंतर नहीं है x = 0 क्योंकि फलन की सीमा f(x) जैसा x 0 की ओर जाता है उपस्थित नहीं है; अभी तक फलन में मध्यवर्ती मूल्य प्रोपर्टी है। कॉनवे बेस 13 फलन द्वारा और अधिक जटिल उदाहरण दिया गया है।
वास्तव में, डार्बौक्स प्रमेय (विश्लेषण) डार्बौक्स प्रमेय कहता है कि कुछ अंतराल पर किसी अन्य फलन के व्युत्पन्न से उत्पन्न होने वाले सभी फलनों में मध्यवर्ती मूल्य प्रोपर्टी होती है (तथापि उन्हें निरंतर होने की आवश्यकता न हो)।
ऐतिहासिक रूप से, इस मध्यवर्ती मूल्य प्रोपर्टी को वास्तविक-मूल्यवान फलनों की निरंतरता की परिभाषा के रूप में सुझाया गया है;[11] इस परिभाषा को नहीं अपनाया गया था।
रचनात्मक गणित में
रचनात्मक गणित में, मध्यवर्ती मान प्रमेय सत्य नहीं है। इसके अतिरिक्त, निष्कर्ष को अशक्त करना है:
- माना और वास्तविक संख्या हो और बंद अंतराल से बिंदुवार निरंतर फलन करें वास्तविक रेखा के लिए, और मान लीजिए कि और . फिर प्रत्येक सकारात्मक संख्या के लिए बिन्दु होता है इकाई अंतराल में जैसे कि है [12]
व्यावहारिक अनुप्रयोग
इसी तरह का परिणाम बोरसुक-उलम प्रमेय है, जो कहता है कि सतत मैप -यूक्लिडियन के लिए क्षेत्र -स्पेस हसदैवमेशा एंटीपोडल पॉइंट्स की कुछ जोड़ी को उसी स्थान पर मैप करता है।
माना किसी वृत्त पर कोई सतत कार्य होना। वृत्त के केंद्र से होकर एक रेखा खींचिए, जो इसे दो विपरीत बिंदुओं पर काटती है और . परिभाषित करें होना .यदि रेखा को 180 डिग्री घुमाया जाए तो मान −d इसके बदले प्राप्त किया जाएगा. मध्यवर्ती मान प्रमेय के कारण जिसके लिए कुछ मध्यवर्ती घूर्णन कोण होना चाहिए d = 0, और परिणामस्वरूप f(A) = f(B) इस कोण पर.
सामान्यतः, किसी भी निरंतर फलन के लिए जिसका डोमेन कुछ बंद उत्तल है -आयाम और आकार के अंदर कोई बिंदु (आवश्यक नहीं कि इसका केंद्र), दिए गए बिंदु के संबंध में दो एंटीपोडल बिंदु उपस्थित हैं जिनका फलनात्मक मूल्य समान है।
प्रमेय इस स्पष्टीकरण को भी रेखांकित करता है कि क्यों घूर्णन तालिका को घूर्णन करने से यह स्थिरता में आ जाएगी (कुछ सरलता से मिलने वाली बाधाओं के अधीन)।[13]
यह भी देखें
- पोंकारे-मिरांडा प्रमेय
- माध्य मान प्रमेय – On the existence of a tangent to an arc parallel to the line through its endpoints
- गैर-परमाणु माप
- हेअरी बॉल प्रमेय
- स्पर्नर की लेम्मा
संदर्भ
- ↑ Weisstein, Eric W. "Bolzano's Theorem". MathWorld.
- ↑ Cates, Dennis M. (2019). Cauchy's Calcul Infinitésimal. p. 249. doi:10.1007/978-3-030-11036-9. ISBN 978-3-030-11035-2. S2CID 132587955.
- ↑ Essentially follows Clarke, Douglas A. (1971). Foundations of Analysis. Appleton-Century-Crofts. p. 284.
- ↑ Sanders, Sam (2017). "Nonstandard Analysis and Constructivism!". arXiv:1704.00281 [math.LO].
- ↑ Bos, Henk J. M. (2001). "The legitimation of geometrical procedures before 1590". Redefining Geometrical Exactness: Descartes' Transformation of the Early Modern Concept of Construction. Sources and Studies in the History of Mathematics and Physical Sciences. New York: Springer. pp. 23–36. doi:10.1007/978-1-4613-0087-8_2. MR 1800805.
- ↑ Russ, S.B. (1980). "A translation of Bolzano's paper on the intermediate value theorem". Historia Mathematica. 7 (2): 156–185. doi:10.1016/0315-0860(80)90036-1.
- ↑ Grabiner, Judith V. (March 1983). "Who Gave You the Epsilon? Cauchy and the Origins of Rigorous Calculus" (PDF). The American Mathematical Monthly. 90 (3): 185–194. doi:10.2307/2975545. JSTOR 2975545.
- ↑ Karin Usadi Katz and Mikhail G. Katz (2011) A Burgessian Critique of Nominalistic Tendencies in Contemporary Mathematics and its Historiography. Foundations of Science. doi:10.1007/s10699-011-9223-1 See link
- ↑ O'Connor, John J.; Robertson, Edmund F., "मध्यवर्ती मूल्य प्रमेय", MacTutor History of Mathematics archive, University of St Andrews
- ↑ Rudin, Walter (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. pp. 42, 93. ISBN 978-0-07-054235-8.
- ↑ Smorynski, Craig (2017-04-07). MVT: A Most Valuable Theorem. Springer. ISBN 9783319529561.
- ↑ Matthew Frank (July 14, 2020). "Interpolating Between Choices for the Approximate Intermediate Value Theorem". Logical Methods in Computer Science. 16 (3). arXiv:1701.02227. doi:10.23638/LMCS-16(3:5)2020.
- ↑ Keith Devlin (2007) How to stabilize a wobbly table
बाहरी संबंध
- मध्यवर्ती मूल्य प्रमेय at ProofWiki
- Intermediate value Theorem - Bolzano Theorem at cut-the-knot
- Bolzano's Theorem by Julio Cesar de la Yncera, Wolfram Demonstrations Project.
- Weisstein, Eric W. "Intermediate Value Theorem". MathWorld.
- Belk, Jim (January 2, 2012). "Two-dimensional version of the Intermediate Value Theorem". Stack Exchange.
- Mizar system proof: http://mizar.org/version/current/html/topreal5.html#T4