सजातीय संबंध

गणित में, एक सजातीय संबंध (जिसे एंडोरेलेशन भी कहा जाता है) एक सेट X पर X और खुद पर एक द्विआधारी संबंध है, यानी यह कार्टेशियन उत्पाद का एक सबसेट है $X \times X$ .^[1]^[2]^[3] इसे आमतौर पर X पर संबंध के रूप में व्यक्त किया जाता है^[4] या एक (द्विआधारी) एक्स पर संबंध।^[5]^[6] सजातीय संबंध का एक उदाहरण रिश्तेदारी का संबंध है, जहां संबंध लोगों पर होता है।

सामान्य प्रकार के एंडोरिलेशन में ऑर्डर (गणित) एस, ग्राफ (असतत गणित) एस, और समकक्ष संबंध शामिल हैं। विशिष्ट अध्ययन आदेश सिद्धांत और ग्राफ सिद्धांत ने एंडोरेलेशन की समझ विकसित की है। ग्राफ़ सिद्धांत के लिए विशेष रूप से शब्दावली का उपयोग वर्णन के लिए किया जाता है, जिसमें एक सामान्य ग्राफ़ को एक सममित संबंध के अनुरूप माना जाता है, और एक निर्देशित ग्राफ़ के अनुरूप एक सामान्य एंडोरेलेशन होता है। एंडोरिलेशन R 0s और 1s के एक तार्किक मैट्रिक्स से मेल खाता है, जहां अभिव्यक्ति xRy ग्राफ में x और y के बीच के किनारे से और R के वर्ग मैट्रिक्स में 1 से मेल खाती है। इसे ग्राफ शब्दावली में एक आसन्न मैट्रिक्स कहा जाता है।

विशेष सजातीय संबंध

एक सेट एक्स पर कुछ विशेष सजातीय संबंध (मनमानी तत्वों के साथ $x 1$ , $x 2$ ) हैं:

खाली रिश्ता *: $E = \emptyset$ ;
यानी, $x 1 Ex 2$ कभी नहीं रखता;
सार्वभौमिक संबंध
$U = X \times X$ ;
यानी, $x 1 Ux 2$ हमेशा धारण करता है;
पहचान संबंध (पहचान समारोह भी देखें)
$I = {(x, x) | x \in X$ };
यानी, $x 1 Ix 2$ अगर और केवल अगर रखता है $x 1 = x 2$ .

उदाहरण

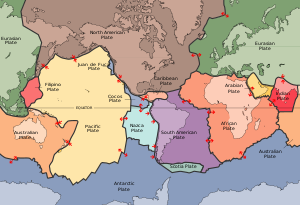
पृथ्वी की पपड़ी की पंद्रह बड़ी विवर्तनिक प्लेटें एक दूसरे से सजातीय संबंध में संपर्क करती हैं। संबंध को तार्किक मैट्रिक्स के रूप में व्यक्त किया जा सकता है जिसमें 1 संकेत संपर्क और 0 कोई संपर्क नहीं है। यह उदाहरण एक सममित संबंध व्यक्त करता है।

गुण

सजातीय संबंध के कुछ महत्वपूर्ण गुण $R$ एक सेट पर $X$ हो सकता है:

Reflexive: सभी के लिए $x \in X$ , $xRx$ . उदाहरण के लिए, ≥ एक स्वतुल्य संबंध है लेकिन > नहीं है।
Irreflexive (या strict): सभी के लिए $x \in X$ , नहीं $xRx$ . उदाहरण के लिए, > एक अप्रासंगिक संबंध है, लेकिन ≥ नहीं है।
Coreflexive: सभी के लिए $x, y \in X$ , अगर $xRy$ तब $x = y$ .^[7] उदाहरण के लिए, पूर्णांकों पर संबंध जिसमें प्रत्येक विषम संख्या स्वयं से संबंधित है, एक मूल संबंध है। समानता संबंध दोनों प्रतिवर्ती और कोरफ्लेक्सिव संबंध का एकमात्र उदाहरण है, और कोई कोरफ्लेक्टिव संबंध पहचान संबंध का एक सबसेट है।
Left quasi-reflexive: सभी के लिए $x, y \in X$ , अगर $xRy$ तब $xRx$ .
Right quasi-reflexive: सभी के लिए $x, y \in X$ , अगर $xRy$ तब $yRy$ .
Quasi-reflexive: सभी के लिए $x, y \in X$ , अगर $xRy$ तब $xRx$ और $yRy$ . एक संबंध अर्ध-प्रतिवर्ती है यदि, और केवल यदि, यह बाएँ और दाएँ अर्ध-प्रतिवर्ती दोनों है।

पिछले 6 विकल्प संपूर्ण होने से बहुत दूर हैं; उदाहरण के लिए, लाल बाइनरी संबंध $y = x 2$ न तो अकाट्य है, न कोरफ्लेक्सिव है, न ही रिफ्लेक्सिव है, क्योंकि इसमें जोड़ी है $(0, 0)$ , और $(2, 4)$ , लेकिन नहीं $(2, 2)$ , क्रमश। बाद के दो तथ्य भी (किसी भी प्रकार की) अर्ध-प्रतिवर्तता से इंकार करते हैं।

Symmetric: सभी के लिए $x, y \in X$ , अगर $xRy$ तब $yRx$ . उदाहरण के लिए, एक रक्त रिश्तेदार एक सममित संबंध है, क्योंकि $x$ का रक्त संबंधी है $y$ अगर और केवल अगर $y$ का रक्त संबंधी है $x$ .
Antisymmetric: सभी के लिए $x, y \in X$ , अगर $xRy$ और $yRx$ तब $x = y$ . उदाहरण के लिए, ≥ एक असममित संबंध है; ऐसा है>, लेकिन रिक्त सत्य (परिभाषा में स्थिति हमेशा गलत होती है)।^[8]
Asymmetric: सभी के लिए $x, y \in X$ , अगर $xRy$ फिर नहीं $yRx$ . एक संबंध असममित है यदि और केवल यदि यह प्रतिसममित और अपरिवर्तनीय दोनों है।^[9] उदाहरण के लिए, > एक असममित संबंध है, लेकिन ≥ नहीं है।

फिर से, पिछले 3 विकल्प संपूर्ण होने से बहुत दूर हैं; प्राकृतिक संख्या, संबंध पर एक उदाहरण के रूप में $xRy$ द्वारा परिभाषित $x > 2$ न तो सममित है और न ही विषम है, अकेले असममित होने दें।

Transitive: सभी के लिए $x, y, z \in X$ , अगर $xRy$ और $yRz$ तब $xRz$ . एक सकर्मक संबंध अपरिवर्तनीय है अगर और केवल अगर यह असममित है।^[10] उदाहरण के लिए, का पूर्वज सकर्मक संबंध है, जबकि का जनक नहीं है।
Antitransitive: सभी के लिए $x, y, z \in X$ , अगर $xRy$ और $yRz$ तो कभी नहीं $xRz$ .
Co-transitive: यदि R का पूरक सकर्मक है। यानी सभी के लिए $x, y, z \in X$ , अगर $xRz$ , तब $xRy$ या $yRz$ . इसका उपयोग रचनात्मक गणित में छद्म क्रम में किया जाता है।
Quasitransitive: सभी के लिए $x, y, z \in X$ , अगर $xRy$ और $yRz$ लेकिन नहीं $yRx$ और न $zRy$ , तब $xRz$ लेकिन नहीं $zRx$ .
Transitivity of incomparability: सभी के लिए $x, y, z \in X$ , अगर $x$ और $y$ के संबंध में अतुलनीय हैं $R$ और यदि ऐसा ही है $y$ और $z$ , तब $x$ और $z$ के संबंध में भी अतुलनीय हैं $R$ . इसका उपयोग कमजोर आदेश में किया जाता है।

पुनः, पिछले 5 विकल्प संपूर्ण नहीं हैं। उदाहरण के लिए, संबंध $xRy$ अगर ( $y = 0$ या $y = x +1$ ) इनमें से किसी भी गुण को संतुष्ट नहीं करता है। दूसरी ओर, खाली रिश्ता उन सभी को तुच्छ रूप से संतुष्ट करता है।

Dense: सभी के लिए $x, y \in X$ ऐसा है कि $xRy$ , कुछ मौजूद है $z \in X$ ऐसा है कि $xRz$ और $zRy$ . इसका उपयोग घने आदेशों में किया जाता है।
Connected: सभी के लिए $x, y \in X$ , अगर $x \neq y$ तब $xRy$ या $yRx$ . यह गुण कभी-कभी होता है^{[citation needed]} जिसे टोटल कहा जाता है, जो नीचे दी गई लेफ्ट/राइट-टोटल की परिभाषाओं से अलग है।
Strongly connected: सभी के लिए $x, y \in X$ , $xRy$ या $yRx$ . यह गुण भी कभी-कभी होता है^{[citation needed]} जिसे टोटल कहा जाता है, जो नीचे दी गई लेफ्ट/राइट-टोटल की परिभाषाओं से अलग है।
Trichotomous: सभी के लिए $x, y \in X$ , बिल्कुल एक $xRy$ , $yRx$ या $x = y$ रखता है। उदाहरण के लिए, > एक त्रिगुणात्मक संबंध है, जबकि प्राकृतिक संख्याओं पर विभाजित संबंध नहीं है।^[11]
Right Euclidean (या केवल Euclidean): सभी के लिए $x, y, z \in X$ , अगर $xRy$ और $xRz$ तब $yRz$ . उदाहरण के लिए, = एक यूक्लिडियन संबंध है क्योंकि यदि $x = y$ और $x = z$ तब $y = z$ .
Left Euclidean: सभी के लिए $x, y, z \in X$ , अगर $yRx$ और $zRx$ तब $yRz$ .
Well-founded: हर गैर-खाली सबसेट $S$ का $X$ के संबंध में अधिकतम और न्यूनतम तत्व शामिल हैं $R$ . अच्छी तरह से स्थापित होने का तात्पर्य अवरोही श्रृंखला की स्थिति से है (अर्थात, कोई अनंत श्रृंखला नहीं है ... $x n R ... Rx 3 Rx 2 Rx 1$ मौजूद हो सकता है)। यदि आश्रित पसंद का स्वयंसिद्ध मान लिया जाए, तो दोनों स्थितियाँ समतुल्य हैं।^[12]^[13]

इसके अलावा, द्विआधारी संबंधों के सभी गुण सामान्य रूप से सजातीय संबंधों पर भी लागू हो सकते हैं:

Set-like: सभी के लिए $x \in X$ , सभी का वर्ग (सेट सिद्धांत)। $y$ ऐसा है कि $yRx$ एक समुच्चय है। (यह तभी समझ में आता है जब उचित वर्गों पर संबंधों की अनुमति हो।)
Left-unique: सभी के लिए $x, z \in X$ और सभी $y \in Y$ , अगर $xRy$ और $zRy$ तब $x = z$ .
Univalent: सभी के लिए $x \in X$ और सभी $y, z \in Y$ , अगर $xRy$ और $xRz$ तब $y = z$ .^[14]
Total (जिसे लेफ्ट-टोटल भी कहा जाता है): सभी के लिए $x \in X$ वहाँ एक मौजूद है $y \in Y$ ऐसा है कि $xRy$ . यह संपत्ति कनेक्टेड की परिभाषा से अलग है (जिसे कुछ लेखकों द्वारा कुल भी कहा जाता है)।^{[citation needed]}
Surjective (जिसे राइट-टोटल भी कहा जाता है): सभी के लिए $y \in Y$ , एक मौजूद है $x \in X$ जैसे कि xRy.

ए preorder एक ऐसा संबंध है जो प्रतिवर्ती और सकर्मक है। ए total preorder, यह भी कहा जाता है linear preorder या weak order, एक ऐसा रिश्ता है जो रिफ्लेक्सिव, सकर्मक और जुड़ा हुआ है।

ए partial order, यह भी कहा जाता है order,^{[citation needed]} एक ऐसा रिश्ता है जो रिफ्लेक्सिव, एंटीसिमेट्रिक और सकर्मक है। ए strict partial order, यह भी कहा जाता है strict order,^{[citation needed]} एक ऐसा संबंध है जो अप्रासंगिक, प्रतिसममित और सकर्मक है। ए total order, यह भी कहा जाता है linear order, simple order, या chain, एक ऐसा रिश्ता है जो रिफ्लेक्सिव, एंटीसिमेट्रिक, सकर्मक और जुड़ा हुआ है।^[15] A strict total order, यह भी कहा जाता है strict linear order, strict simple order, या strict chain, एक ऐसा संबंध है जो अप्रतिवर्ती, प्रतिसममित, सकर्मक और जुड़ा हुआ है।

ए partial equivalence relation एक संबंध है जो सममित और सकर्मक है। एक equivalence relation एक ऐसा संबंध है जो प्रतिवर्त, सममित और सकर्मक है। यह एक ऐसा संबंध भी है जो सममित, सकर्मक और कुल है, क्योंकि ये गुण रिफ्लेक्सिविटी का संकेत देते हैं।

Implications and conflicts between properties of homogeneous binary relations
Implications (blue) and conflicts (red) between properties (yellow) of homogeneous binary relations. For example, every asymmetric relation is irreflexive ("ASym ⇒ Irrefl"), and no relation on a non-empty set can be both irreflexive and reflexive ("Irrefl # Refl"). Omitting the red edges results in a Hasse diagram.

संचालन

यदि R एक सेट X पर एक सजातीय संबंध है तो निम्नलिखित में से प्रत्येक X पर एक सजातीय संबंध है:

Reflexive closure, आर⁼: $R के रूप में परिभाषित =</सुप> = {(एक्स, एक्स) | x \in X} \cup R$ या R युक्त X पर सबसे छोटा रिफ्लेक्सिव संबंध। यह R वाले सभी रिफ्लेक्सिव संबंधों के प्रतिच्छेदन (सेट सिद्धांत) के बराबर साबित हो सकता है।
Reflexive reduction, आर^≠: $R के तौर पर परिभाषित किया गया है≠ = R \ {(x, x) | x ∈ X}$ या R में निहित X पर सबसे बड़ा अप्रासंगिक संबंध।
Transitive closure, आर⁺: R वाले X पर सबसे छोटे सकर्मक संबंध के रूप में परिभाषित किया गया है। इसे R वाले सभी सकर्मक संबंधों के प्रतिच्छेदन के बराबर देखा जा सकता है।
Reflexive transitive closure, आर*: के रूप में परिभाषित $R * = (R +) =$ , सबसे छोटा पूर्व आदेश जिसमें R है।
Reflexive transitive symmetric closure, आर^≡: R वाले X पर सबसे छोटे समतुल्य संबंध के रूप में परिभाषित।

में परिभाषित सभी ऑपरेशन Binary relation § Operations on binary relations सजातीय संबंधों पर भी लागू होता है।

Homogeneous relations by property
	Reflexivity	Symmetry	Transitivity	Connectedness	Symbol	Example
Directed graph					→
Undirected graph		Symmetric
Dependency	Reflexive	Symmetric
Tournament	Irreflexive	Asymmetric				Pecking order
Preorder	Reflexive		Transitive		≤	Preference
Total preorder	Reflexive		Transitive	Connected	≤
Partial order	Reflexive	Antisymmetric	Transitive		≤	Subset
Strict partial order	Irreflexive	Asymmetric	Transitive		<	Strict subset
Total order	Reflexive	Antisymmetric	Transitive	Connected	≤	Alphabetical order
Strict total order	Irreflexive	Asymmetric	Transitive	Connected	<	Strict alphabetical order
Partial equivalence relation		Symmetric	Transitive
Equivalence relation	Reflexive	Symmetric	Transitive		∼, ≡	Equality

गणना

सभी सजातीय संबंधों का सेट ${\mathcal {B}}(X)$ एक समुच्चय के ऊपर X समुच्चय है $2 X \times X$ जो कि एक बूलियन बीजगणित (संरचना) है जो इसके विपरीत संबंध के संबंध के मानचित्रण के समावेशन (गणित) के साथ संवर्धित है। संबंधों की संरचना को एक बाइनरी ऑपरेशन के रूप में देखते हुए ${\mathcal {B}}(X)$ , यह समावेशन के साथ एक मोनोइड बनाता है जहां पहचान तत्व पहचान संबंध है।^[16] एक एन-एलिमेंट सेट पर अलग-अलग सजातीय संबंधों की संख्या है $2 n 2$ (sequence A002416 in the OEIS):

Number of n-element binary relations of different types
Elements	Any	Transitive	Reflexive	Symmetric	Preorder	Partial order	Total preorder	Total order	Equivalence relation
0	1	1	1	1	1	1	1	1	1
1	2	2	1	2	1	1	1	1	1
2	16	13	4	8	4	3	3	2	2
3	512	171	64	64	29	19	13	6	5
4	65,536	3,994	4,096	1,024	355	219	75	24	15
n	2^n²		2^n²−n	2^n(n+1)/2			${\textstyle \sum _{k=0}^{n}k!S(n,k)}$	n!	${\textstyle \sum _{k=0}^{n}S(n,k)}$
OEIS	A002416	A006905	A053763	A006125	A000798	A001035	A000670	A000142	A000110

Note that $S (n, k)$ refers to Stirling numbers of the second kind.

टिप्पणियाँ:

अप्रासंगिक संबंधों की संख्या वही है जो प्रतिवर्ती संबंधों की है।
आंशिक रूप से आदेशित सेट की संख्या # सख्त और गैर-सख्त आंशिक आदेश संबंधों (अपरिवर्तनीय सकर्मक संबंध) के अनुरूप आंशिक आदेश के समान है।
सख्त कमजोर ऑर्डर की संख्या कुल प्रीऑर्डर की संख्या के समान है।
कुल ऑर्डर आंशिक ऑर्डर होते हैं जो कुल प्रीऑर्डर भी होते हैं। ऐसे प्रीऑर्डर्स की संख्या जो न तो आंशिक ऑर्डर हैं और न ही कुल प्रीऑर्डर, इसलिए, प्रीऑर्डर्स की संख्या, माइनस आंशिक ऑर्डर्स की संख्या, माइनस कुल प्रीऑर्डर्स की संख्या, प्लस कुल ऑर्डर्स की संख्या: 0, 0, 0, क्रमशः 3, और 85।
तुल्यता संबंधों की संख्या एक सेट के विभाजन की संख्या है, जो बेल संख्या है।

सजातीय संबंधों को जोड़ों में बांटा जा सकता है (संबंध, द्विआधारी संबंध # पूरक), इसके अलावा $n = 0$ संबंध अपना ही पूरक होता है। गैर-सममित वाले को 4-टपल (संबंध, पूरक, बाइनरी संबंधों पर #ऑपरेशन, व्युत्क्रम पूरक) में बांटा जा सकता है।

उदाहरण

सख्त आदेश सहित आदेश संबंध:
- से अधिक
- इससे बड़ा या इसके बराबर
- से कम
- से कम या बराबर
- विभाजित (समान रूप से)
- का भाग
तुल्यता संबंध:
- समानता (गणित)
- समानांतर (ज्यामिति) के साथ (एफ़िन रिक्त स्थान के लिए)
- समतुल्यता या आपत्ति में है
- समरूपता
- संतुलन (ज्यामिति)
टॉलरेंस रिलेशन, एक रिफ्लेक्सिव और सिमेट्रिक रिलेशन:
- निर्भरता संबंध, एक परिमित सहिष्णुता संबंध
- स्वतंत्रता संबंध, कुछ निर्भरता संबंध का पूरक
रिश्तेदारी#संबंधों की संरचना

सामान्यीकरण

सामान्य रूप से एक द्विआधारी संबंध को सजातीय होने की आवश्यकता नहीं है, इसे मनमाने सेट X और Y के लिए एक उपसमुच्चय R ⊆ X × Y के रूप में परिभाषित किया गया है।
एक परिमित संबंध एक उपसमुच्चय R ⊆ X है₁ × ... × एक्स_n कुछ प्राकृतिक संख्या n और मनमाना सेट X के लिए₁, ..., एक्स_n, इसे n-ary संबंध भी कहते हैं।

संदर्भ

↑ Michael Winter (2007). Goguen Categories: A Categorical Approach to L-fuzzy Relations. Springer. pp. x–xi. ISBN 978-1-4020-6164-6.
↑ M. E. Müller (2012). संबंधपरक ज्ञान की खोज. Cambridge University Press. p. 22. ISBN 978-0-521-19021-3.
↑ Peter J. Pahl; Rudolf Damrath (2001). Mathematical Foundations of Computational Engineering: A Handbook. Springer Science & Business Media. p. 496. ISBN 978-3-540-67995-0.
↑ Mordeson, John N.; Nair, Premchand S. (8 November 2012). Fuzzy Mathematics: An Introduction for Engineers and Scientists. Physica. p. 2. ISBN 978-3-7908-1808-6.
↑ Tanaev, V.; Gordon, W.; Shafransky, Yakov M. (6 December 2012). समयबद्धन सिद्धांत। सिंगल-स्टेज सिस्टम. Springer Science & Business Media. p. 41. ISBN 978-94-011-1190-4.
↑ Meyer, Bertrand (29 June 2009). Touch of Class: Learning to Program Well with Objects and Contracts. Springer Science & Business Media. p. 509. ISBN 978-3-540-92145-5.
↑ Fonseca de Oliveira, J. N., & Pereira Cunha Rodrigues, C. D. J. (2004). Transposing Relations: From Maybe Functions to Hash Tables. In Mathematics of Program Construction (p. 337).
↑ Smith, Douglas; Eggen, Maurice; St. Andre, Richard (2006), A Transition to Advanced Mathematics (6th ed.), Brooks/Cole, p. 160, ISBN 0-534-39900-2
↑ Nievergelt, Yves (2002), Foundations of Logic and Mathematics: Applications to Computer Science and Cryptography, Springer-Verlag, p. 158.
↑ Flaška, V.; Ježek, J.; Kepka, T.; Kortelainen, J. (2007). बाइनरी रिलेशंस का सकर्मक क्लोजर I (PDF). Prague: School of Mathematics – Physics Charles University. p. 1. Archived from the original (PDF) on 2013-11-02. Lemma 1.1 (iv). This source refers to asymmetric relations as "strictly antisymmetric".
↑ Since neither 5 divides 3, nor 3 divides 5, nor 3=5.
↑ "अच्छी तरह से स्थापित होने की स्थिति". ProofWiki. Archived from the original on 20 February 2019. Retrieved 20 February 2019.
↑ Fraisse, R. (15 December 2000). Theory of Relations, Volume 145 - 1st Edition (1st ed.). Elsevier. p. 46. ISBN 9780444505422. Retrieved 20 February 2019.
↑ Gunther Schmidt & Thomas Strohlein (2012)[1987] Relations and Graphs, p. 54, at Google Books
↑ Joseph G. Rosenstein, Linear orderings, Academic Press, 1982, ISBN 0-12-597680-1, p. 4
↑ Schmidt, Gunther; Ströhlein, Thomas (1993). "Homogeneous Relations". Relations and Graphs: Discrete Mathematics for Computer Scientists. Berlin, Heidelberg: Springer. p. 14. doi:10.1007/978-3-642-77968-8_2. ISBN 978-3-642-77968-8.

[Winter2007-1] Michael Winter (2007). Goguen Categories: A Categorical Approach to L-fuzzy Relations. Springer. pp. x–xi. ISBN 978-1-4020-6164-6.

[M.C3.BCller2012-2] M. E. Müller (2012). संबंधपरक ज्ञान की खोज. Cambridge University Press. p. 22. ISBN 978-0-521-19021-3.

[PahlDamrath2001-p496-3] Peter J. Pahl; Rudolf Damrath (2001). Mathematical Foundations of Computational Engineering: A Handbook. Springer Science & Business Media. p. 496. ISBN 978-3-540-67995-0.

[4] Mordeson, John N.; Nair, Premchand S. (8 November 2012). Fuzzy Mathematics: An Introduction for Engineers and Scientists. Physica. p. 2. ISBN 978-3-7908-1808-6.

[5] Tanaev, V.; Gordon, W.; Shafransky, Yakov M. (6 December 2012). समयबद्धन सिद्धांत। सिंगल-स्टेज सिस्टम. Springer Science & Business Media. p. 41. ISBN 978-94-011-1190-4.

[6] Meyer, Bertrand (29 June 2009). Touch of Class: Learning to Program Well with Objects and Contracts. Springer Science & Business Media. p. 509. ISBN 978-3-540-92145-5.

[7] Fonseca de Oliveira, J. N., & Pereira Cunha Rodrigues, C. D. J. (2004). Transposing Relations: From Maybe Functions to Hash Tables. In Mathematics of Program Construction (p. 337).

[8] Smith, Douglas; Eggen, Maurice; St. Andre, Richard (2006), A Transition to Advanced Mathematics (6th ed.), Brooks/Cole, p. 160, ISBN 0-534-39900-2

[9] Nievergelt, Yves (2002), Foundations of Logic and Mathematics: Applications to Computer Science and Cryptography, Springer-Verlag, p. 158.

[10] Flaška, V.; Ježek, J.; Kepka, T.; Kortelainen, J. (2007). बाइनरी रिलेशंस का सकर्मक क्लोजर I (PDF). Prague: School of Mathematics – Physics Charles University. p. 1. Archived from the original (PDF) on 2013-11-02. Lemma 1.1 (iv). This source refers to asymmetric relations as "strictly antisymmetric".

[11] Since neither 5 divides 3, nor 3 divides 5, nor 3=5.

[12] "अच्छी तरह से स्थापित होने की स्थिति". ProofWiki. Archived from the original on 20 February 2019. Retrieved 20 February 2019.

[13] Fraisse, R. (15 December 2000). Theory of Relations, Volume 145 - 1st Edition (1st ed.). Elsevier. p. 46. ISBN 9780444505422. Retrieved 20 February 2019.

[14] Gunther Schmidt & Thomas Strohlein (2012)[1987] Relations and Graphs, p. 54, at Google Books

[15] Joseph G. Rosenstein, Linear orderings, Academic Press, 1982, ISBN 0-12-597680-1, p. 4

[16] Schmidt, Gunther; Ströhlein, Thomas (1993). "Homogeneous Relations". Relations and Graphs: Discrete Mathematics for Computer Scientists. Berlin, Heidelberg: Springer. p. 14. doi:10.1007/978-3-642-77968-8_2. ISBN 978-3-642-77968-8.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

सजातीय संबंध

Contents

विशेष सजातीय संबंध

उदाहरण

गुण

संचालन

गणना

उदाहरण

सामान्यीकरण

संदर्भ

Navigation menu

Search