हाइजेनबर्ग समूह

गणित में, हाइजेनबर्ग समूह $H$, वर्नर हाइजेनबर्ग के नाम पर, फॉर्म के 3 × 3 त्रिकोणीय मैट्रिक्स का समूह (गणित) है

${\begin{pmatrix}1&a&c\\0&1&b\\0&0&1\\\end{pmatrix}}$

मैट्रिक्स गुणा के संचालन के तहत। तत्व ए, बी और सी को पहचान के साथ किसी भी क्रमविनिमेय अंगूठी से लिया जा सकता है, जिसे अक्सर वास्तविक संख्याओं की अंगूठी (जिसके परिणामस्वरूप निरंतर हाइजेनबर्ग समूह होता है) या पूर्णांक की अंगूठी (जिसके परिणामस्वरूप असतत हाइजेनबर्ग समूह होता है) के रूप में लिया जाता है।

निरंतर हाइजेनबर्ग समूह एक आयामी क्वांटम यांत्रिक सिस्टम के विवरण में उत्पन्न होता है, विशेष रूप से स्टोन-वॉन न्यूमैन प्रमेय के संदर्भ में। अधिक आम तौर पर, हाइजेनबर्ग समूहों को एन-डायमेंशनल सिस्टम से जुड़ा माना जा सकता है, और सबसे आम तौर पर, किसी भी सहानुभूतिपूर्ण वेक्टर स्पेस के लिए।

त्रि-आयामी मामला

त्रि-आयामी मामले में, दो हाइजेनबर्ग मैट्रिक्स का उत्पाद निम्न द्वारा दिया जाता है:

${\begin{pmatrix}1&a&c\\0&1&b\\0&0&1\\\end{pmatrix}}{\begin{pmatrix}1&a'&c'\\0&1&b'\\0&0&1\\\end{pmatrix}}={\begin{pmatrix}1&a+a'&c+ab'+c'\\0&1&b+b'\\0&0&1\\\end{pmatrix}}\,.$

जैसा कि शब्द से देखा जा सकता है ab', समूह गैर-अबेलियन समूह|गैर-अबेलियन है।

हाइजेनबर्ग समूह का तटस्थ तत्व पहचान मैट्रिक्स है, और व्युत्क्रम द्वारा दिया जाता है

${\begin{pmatrix}1&a&c\\0&1&b\\0&0&1\\\end{pmatrix}}^{-1}={\begin{pmatrix}1&-a&ab-c\\0&1&-b\\0&0&1\\\end{pmatrix}}\,.$

समूह द्वि-आयामी संबंध समूह Aff(2) का एक उपसमूह है: ${\begin{pmatrix}1&a&c\\0&1&b\\0&0&1\\\end{pmatrix}}$ अभिनय कर रहे $({\vec {x}},1)$ affine परिवर्तन के अनुरूप है ${\begin{pmatrix}1&a\\0&1\end{pmatrix}}{\vec {x}}+{\begin{pmatrix}c\\b\end{pmatrix}}$.

त्रि-आयामी मामले के कई प्रमुख उदाहरण हैं।

सतत हाइजेनबर्ग समूह

अगर a, b, c, वास्तविक संख्याएँ हैं (रिंग R में) तो किसी के पास निरंतर हाइजेनबर्ग समूह H है₃(आर)।

यह डायमेंशन 3 का एक निलपोटेंट समूह रियल झूठ समूह है।

वास्तविक 3×3 मैट्रिसेस के रूप में प्रतिनिधित्व के अलावा, निरंतर हाइजेनबर्ग समूह में कार्य स्थान के संदर्भ में कई अलग-अलग समूह प्रतिनिधित्व भी हैं। स्टोन-वॉन न्यूमैन प्रमेय द्वारा, आइसोमोर्फिज्म तक, एच का एक अनूठा इरेड्यूसेबल एकात्मक प्रतिनिधित्व है जिसमें एक समूह का केंद्र एक दिए गए गैर-तुच्छ चरित्र सिद्धांत द्वारा कार्य करता है। इस प्रतिनिधित्व में कई महत्वपूर्ण अहसास या मॉडल हैं। श्रोडिंगर मॉडल में, हाइजेनबर्ग समूह वर्ग समाकलनीय कार्यों के स्थान पर कार्य करता है। थीटा प्रतिनिधित्व में, यह ऊपरी अर्ध-तल पर होलोमॉर्फिक फ़ंक्शन के स्थान पर कार्य करता है; थीटा प्रकार्यों के साथ इसके संबंध के कारण इसे यह नाम दिया गया है।

असतत हाइजेनबर्ग समूह

असतत हाइजेनबर्ग समूह के केली ग्राफ का एक हिस्सा, जेनरेटर x, y, z जैसा कि पाठ में है। (रंग केवल दृश्य सहायता के लिए है।)

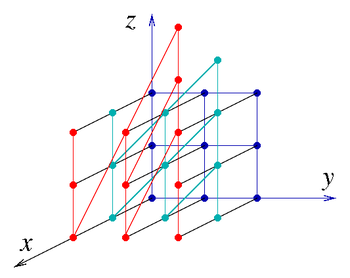
अगर a, b, c, पूर्णांक हैं (रिंग Z में) तो किसी के पास असतत हाइजेनबर्ग समूह H है₃(जेड)। यह एक गैर-अबेलियन समूह|नॉन-एबेलियन निलपोटेंट ग्रुप है। इसके दो जनरेटर हैं,

$x={\begin{pmatrix}1&1&0\\0&1&0\\0&0&1\\\end{pmatrix}},\ \ y={\begin{pmatrix}1&0&0\\0&1&1\\0&0&1\\\end{pmatrix}}$

और संबंध

$z_{}^{}=xyx^{-1}y^{-1},\ xz=zx,\ yz=zy$,

कहाँ

$z={\begin{pmatrix}1&0&1\\0&1&0\\0&0&1\\\end{pmatrix}}$

एच के समूह के केंद्र का जनरेटर है₃. (ध्यान दें कि x, y, और z के व्युत्क्रम विकर्ण के ऊपर 1 को −1 से बदल देते हैं।)

बास के प्रमेय के अनुसार, इसकी क्रम 4 की बहुपद विकास दर (समूह सिद्धांत) है।

के माध्यम से कोई भी तत्व उत्पन्न कर सकता है

${\begin{pmatrix}1&a&c\\0&1&b\\0&0&1\\\end{pmatrix}}=y^{b}z^{c}x^{a}\,.$

हाइजेनबर्ग समूह सापेक्ष एक विषम अभाज्य p

यदि कोई मॉड्यूलर अंकगणित में a, b, c लेता है | 'Z'/p 'Z' एक विषम अभाज्य संख्या p के लिए है, तो उसके पास 'हाइजेनबर्ग समूह मॉड्यूलो' 'p' है। यह आदेश का एक समूह है (समूह सिद्धांत) पी³ जनरेटर x, y और संबंधों के साथ:

$z_{}^{}=xyx^{-1}y^{-1},\ x^{p}=y^{p}=z^{p}=1,\ xz=zx,\ yz=zy.$

विषम प्राइम ऑर्डर पी के परिमित क्षेत्रों पर हाइजेनबर्ग समूहों के एनालॉग को अतिरिक्त विशेष समूह कहा जाता है, या अधिक ठीक से, प्रतिपादक के अतिरिक्त विशेष समूह (समूह सिद्धांत) पी। अधिक आम तौर पर, यदि समूह G का व्युत्पन्न उपसमूह G के केंद्र Z में समाहित है, तो G/Z × G/Z → Z से मानचित्र एबेलियन समूहों पर एक तिरछा-सममित बिलिनियर ऑपरेटर है।

हालाँकि, यह आवश्यक है कि G/Z एक परिमित सदिश स्थान हो, इसके लिए G के फ्रैटिनी उपसमूह को केंद्र में समाहित करने की आवश्यकता है, और यह आवश्यक है कि Z 'Z'/p 'Z' पर एक-आयामी वेक्टर स्थान हो, जिसके लिए Z की आवश्यकता है ऑर्डर पी, इसलिए यदि जी एबेलियन नहीं है, तो जी अतिरिक्त विशेष है। यदि जी अतिरिक्त विशेष है लेकिन इसमें एक्सपोनेंट पी नहीं है, तो नीचे दिए गए सामान्य निर्माण को सिम्पलेक्टिक सदिश स्थल जी/जेड पर लागू किया जाता है जो जी के लिए समूह आइसोमोर्फिक उत्पन्न नहीं करता है।

हाइजेनबर्ग समूह मॉड्यूल 2

हाइजेनबर्ग समूह मॉड्यूलो 2 ऑर्डर 8 का है और डायहेड्रल समूह डी के लिए आइसोमोर्फिक है₄ (एक वर्ग की समरूपता)। गौर करें कि अगर

$x={\begin{pmatrix}1&1&0\\0&1&0\\0&0&1\\\end{pmatrix}},\ \ y={\begin{pmatrix}1&0&0\\0&1&1\\0&0&1\\\end{pmatrix}}$.

तब

$xy={\begin{pmatrix}1&1&1\\0&1&1\\0&0&1\\\end{pmatrix}},$

और

$yx={\begin{pmatrix}1&1&0\\0&1&1\\0&0&1\\\end{pmatrix}}.$

तत्व x और y परावर्तन के संगत हैं (उनके बीच 45° के साथ), जबकि xy और yx 90° के घूर्णन के अनुरूप हैं। अन्य प्रतिबिंब xyx और yxy हैं, और 180 डिग्री रोटेशन xyxy (=yxyx) है।

हाइजेनबर्ग बीजगणित

झूठ बीजगणित ${\mathfrak {h}}$ हाइजेनबर्ग समूह के $H$ (वास्तविक संख्याओं पर) हाइजेनबर्ग बीजगणित के रूप में जाना जाता है। इसे फॉर्म के 3×3 मैट्रिक्स के स्थान का उपयोग करके प्रदर्शित किया जा सकता है

${\begin{pmatrix}0&a&c\\0&0&b\\0&0&0\\\end{pmatrix}},$

साथ $a,b,c\in \mathbb {R}$.

निम्नलिखित तीन तत्व आधार बनाते हैं ${\mathfrak {h}}$,

$X={\begin{pmatrix}0&1&0\\0&0&0\\0&0&0\\\end{pmatrix}};\quad Y={\begin{pmatrix}0&0&0\\0&0&1\\0&0&0\\\end{pmatrix}};\quad Z={\begin{pmatrix}0&0&1\\0&0&0\\0&0&0\\\end{pmatrix}}.$

ये आधार तत्व रूपांतरण संबंधों को संतुष्ट करते हैं,

$[X,Y]=Z;\quad [X,Z]=0;\quad [Y,Z]=0$.

हाइजेनबर्ग समूह का नाम पूर्ववर्ती संबंधों से प्रेरित है, जो क्वांटम यांत्रिकी विहित रूपान्तरण संबंध संबंधों के समान रूप है,

$\left[{\hat {x}},{\hat {p}}\right]=i\hbar I;\quad \left[{\hat {x}},i\hbar I\right]=0;\quad \left[{\hat {p}},i\hbar I\right]=0,$

कहाँ ${\hat {x}}$ स्थिति संचालिका है, ${\hat {p}}$ संवेग संचालक है, और $\hbar$ प्लैंक नियतांक है।

हाइजेनबर्ग समूह H में विशेष संपत्ति है कि घातीय मानचित्र एक-से-एक है और लाई बीजगणित से मानचित्र पर है ${\mathfrak {h}}$ समूह को H,

$\exp {\begin{pmatrix}0&a&c\\0&0&b\\0&0&0\\\end{pmatrix}}={\begin{pmatrix}1&a&c+{\frac {ab}{2}}\\0&1&b\\0&0&1\\\end{pmatrix}}.$

अनुरूप क्षेत्र सिद्धांत में

अनुरूप क्षेत्र सिद्धांत में, हाइजेनबर्ग बीजगणित शब्द का प्रयोग उपरोक्त बीजगणित के अनंत-आयामी सामान्यीकरण के संदर्भ में किया जाता है। यह तत्वों द्वारा फैला हुआ है $a_{n},n\in \mathbb {Z}$, रूपान्तरण संबंधों के साथ

$[a_{n},a_{m}]=n\delta _{n+m,0}.$

एक पुनर्विक्रय के तहत, यह उपरोक्त बीजगणित की प्रतियों की एक अनगिनत-अनंत संख्या है।

उच्च आयाम

अधिक सामान्य हाइजेनबर्ग समूह $H_{2n+1}$ यूक्लिडियन अंतरिक्ष में उच्च आयामों के लिए परिभाषित किया जा सकता है, और आमतौर पर सहानुभूतिपूर्ण वेक्टर रिक्त स्थान पर। सबसे सरल सामान्य मामला आयाम का वास्तविक हाइजेनबर्ग समूह है $2n+1$, किसी भी पूर्णांक के लिए $n\geq 1$. मेट्रिसेस के समूह के रूप में, $H_{2n+1}$ (या $H_{2n+1}(\mathbb {R} )$ यह इंगित करने के लिए कि यह क्षेत्र के ऊपर हाइजेनबर्ग समूह है $\mathbb {R}$ वास्तविक संख्याओं का) समूह के रूप में परिभाषित किया गया है $(n+2)\times (n+2)$ में प्रविष्टियों के साथ मैट्रिसेस $\mathbb {R}$ और फॉर्म होना:

${\begin{bmatrix}1&\mathbf {a} &c\\\mathbf {0} &I_{n}&\mathbf {b} \\0&\mathbf {0} &1\end{bmatrix}}$

कहाँ

a लंबाई n का एक पंक्ति सदिश है,

b लंबाई n का एक स्तंभ सदिश है,

मैं_n आकार n की पहचान मैट्रिक्स है।

समूह संरचना

यह वास्तव में एक समूह है, जैसा कि गुणन द्वारा दिखाया गया है:

${\begin{bmatrix}1&\mathbf {a} &c\\0&I_{n}&\mathbf {b} \\0&0&1\end{bmatrix}}\cdot {\begin{bmatrix}1&\mathbf {a} '&c'\\0&I_{n}&\mathbf {b} '\\0&0&1\end{bmatrix}}={\begin{bmatrix}1&\mathbf {a} +\mathbf {a} '&c+c'+\mathbf {a} \cdot \mathbf {b} '\\0&I_{n}&\mathbf {b} +\mathbf {b} '\\0&0&1\end{bmatrix}}$

और

${\begin{bmatrix}1&\mathbf {a} &c\\0&I_{n}&\mathbf {b} \\0&0&1\end{bmatrix}}\cdot {\begin{bmatrix}1&-\mathbf {a} &-c+\mathbf {a} \cdot \mathbf {b} \\0&I_{n}&-\mathbf {b} \\0&0&1\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&I_{n}&0\\0&0&1\end{bmatrix}}.$

झूठ बीजगणित

हाइजेनबर्ग समूह एक सरलता से जुड़ा हुआ झूठ ​​समूह है जिसका झूठ बीजगणित मेट्रिसेस के होते हैं

${\begin{bmatrix}0&\mathbf {a} &c\\0&0_{n}&\mathbf {b} \\0&0&0\end{bmatrix}},$

कहाँ

a लंबाई n का एक पंक्ति सदिश है,

b लंबाई n का एक स्तंभ सदिश है,

0_n आकार n का शून्य मैट्रिक्स है।

इ देकर₁, ..., यह है_n R का विहित आधार होⁿ, और सेटिंग

${\begin{aligned}p_{i}&={\begin{bmatrix}0&\operatorname {e} _{i}^{\mathrm {T} }&0\\0&0_{n}&0\\0&0&0\end{bmatrix}},\\q_{j}&={\begin{bmatrix}0&0&0\\0&0_{n}&\operatorname {e} _{j}\\0&0&0\end{bmatrix}},\\z&={\begin{bmatrix}0&0&1\\0&0_{n}&0\\0&0&0\end{bmatrix}},\end{aligned}}$

संबद्ध झूठ बीजगणित को विहित रूपान्तरण संबंधों द्वारा चित्रित किया जा सकता है,

${\begin{bmatrix}p_{i},q_{j}\end{bmatrix}}=\delta _{ij}z,\qquad {\begin{bmatrix}p_{i},z\end{bmatrix}}=0,\qquad {\begin{bmatrix}q_{j},z\end{bmatrix}}=0~,$

(1)

जहां प₁, ..., पी_n, क्यू₁, ..., क्यू_n, z बीजगणित जनक हैं।

विशेष रूप से, z हाइजेनबर्ग लाइ बीजगणित का एक केंद्रीय तत्व है। ध्यान दें कि हाइजेनबर्ग समूह का लाई बीजगणित शून्य है।

घातीय मानचित्र

होने देना

$u={\begin{bmatrix}0&\mathbf {a} &c\\0&0_{n}&\mathbf {b} \\0&0&0\end{bmatrix}},$

जो पूरा करता है $u^{3}=0_{n+2}$. एक्सपोनेंशियल मैप (लेट थ्योरी) का मूल्यांकन करता है

$\exp(u)=\sum _{k=0}^{\infty }{\frac {1}{k!}}u^{k}=I_{n+2}+u+{\tfrac {1}{2}}u^{2}={\begin{bmatrix}1&\mathbf {a} &c+{1 \over 2}\mathbf {a} \cdot \mathbf {b} \\0&I_{n}&\mathbf {b} \\0&0&1\end{bmatrix}}.$

किसी भी नीलपोटेंट लाई बीजगणित का घातीय मानचित्र लाई बीजगणित और अद्वितीय संबद्ध जुड़े स्थान, बस-जुड़े झूठ समूह के बीच एक भिन्नता है।

यह चर्चा (आयाम और लाई समूह से संबंधित कथनों को छोड़कर) आगे लागू होती है यदि हम R को किसी क्रमविनिमेय वलय A से प्रतिस्थापित करते हैं। संबंधित समूह को एच से निरूपित किया जाता है_n(ए )।

अतिरिक्त धारणा के तहत कि अभाज्य 2 वलय A में व्युत्क्रमणीय है, चरघातांकी मानचित्र को भी परिभाषित किया गया है, क्योंकि यह एक परिमित योग में घटता है और ऊपर का रूप है (उदाहरण के लिए A एक वलय 'Z'/p 'Z' हो सकता है जिसमें एक विषम अभाज्य p या विशेषता (बीजगणित) 0 का कोई क्षेत्र (गणित)।

प्रतिनिधित्व सिद्धांत

Main article: Stone–von Neumann theorem

हाइजेनबर्ग समूह का एकात्मक लाइ समूह प्रतिनिधित्व काफी सरल है - बाद में मैके सिद्धांत द्वारा सामान्यीकृत - और क्वांटम भौतिकी में इसकी शुरुआत के लिए प्रेरणा थी, जैसा कि नीचे चर्चा की गई है।

प्रत्येक अशून्य वास्तविक संख्या के लिए $\hbar$, हम एक अलघुकरणीय एकात्मक प्रतिनिधित्व को परिभाषित कर सकते हैं $\Pi _{\hbar }$ का $H_{2n+1}$ हिल्बर्ट अंतरिक्ष पर अभिनय $L^{2}(\mathbb {R} ^{n})$ सूत्र द्वारा:

$\left[\Pi _{\hbar }{\begin{pmatrix}1&\mathbf {a} &c\\0&I_{n}&\mathbf {b} \\0&0&1\end{pmatrix}}\psi \right](x)=e^{i\hbar c}e^{ib\cdot x}\psi (x+\hbar a)$

इस प्रतिनिधित्व को थरथरानवाला प्रतिनिधित्व के रूप में जाना जाता है # हाइजेनबर्ग और वेइल के कम्यूटेशन संबंध | श्रोडिंगर प्रतिनिधित्व। इस प्रतिनिधित्व के लिए प्रेरणा क्वांटम यांत्रिकी में प्रतिपादक स्थिति ऑपरेटर और संवेग ऑपरेटरों की कार्रवाई है। पैरामीटर $a$ स्थिति स्थान, पैरामीटर में अनुवाद का वर्णन करता है $b$ गति स्थान और पैरामीटर में अनुवाद का वर्णन करता है $c$ एक समग्र चरण कारक देता है। ऑपरेटरों के एक समूह को प्राप्त करने के लिए चरण कारक की आवश्यकता होती है, क्योंकि स्थिति स्थान में अनुवाद और गति स्थान में अनुवाद कम्यूट नहीं करते हैं।

मुख्य परिणाम स्टोन-वॉन न्यूमैन प्रमेय है, जिसमें कहा गया है कि हाइजेनबर्ग समूह का प्रत्येक (दृढ़ता से निरंतर) अप्रासंगिक एकात्मक प्रतिनिधित्व जिसमें केंद्र गैर-तुच्छ रूप से कार्य करता है, के बराबर है $\Pi _{\hbar }$ कुछ के लिए $\hbar$. वैकल्पिक रूप से, कि वे सभी आयाम 2n के एक सहानुभूतिपूर्ण स्थान पर वेइल बीजगणित (या CCR बीजगणित) के समतुल्य हैं।

चूंकि हाइजेनबर्ग समूह का एक आयामी केंद्रीय विस्तार है $\mathbb {R} ^{2n}$, इसके अप्रासंगिक एकात्मक अभ्यावेदन को अप्रासंगिक एकात्मक प्रक्षेप्य अभ्यावेदन के रूप में देखा जा सकता है $\mathbb {R} ^{2n}$. संकल्पनात्मक रूप से, ऊपर दिया गया प्रतिनिधित्व शास्त्रीय चरण स्थान पर ट्रांसलेशनल समरूपता के समूह के लिए क्वांटम मैकेनिकल समकक्ष का गठन करता है, $\mathbb {R} ^{2n}$. तथ्य यह है कि क्वांटम संस्करण का केवल एक अनुमानित प्रतिनिधित्व है $\mathbb {R} ^{2n}$ शास्त्रीय स्तर पर पहले से ही सुझाव दिया गया है। चरण स्थान में अनुवाद के हैमिल्टनियन जनरेटर स्थिति और संवेग कार्य हैं। हालांकि, इन कार्यों की अवधि पॉइसन ब्रैकेट के तहत झूठ बीजगणित नहीं बनाती है, क्योंकि $\{x_{i},p_{j}\}=\delta _{i,j}.$ बल्कि, स्थिति और संवेग कार्यों की अवधि और स्थिरांक पॉसॉन ब्रैकेट के तहत एक झूठ बीजगणित बनाते हैं। यह लाई बीजगणित क्रमविनिमेय लाई बीजगणित का एक आयामी केंद्रीय विस्तार है $\mathbb {R} ^{2n}$, हाइजेनबर्ग समूह के लाइ बीजगणित के लिए समरूप।

सहानुभूतिपूर्ण वेक्टर रिक्त स्थान पर

हाइजेनबर्ग समूह का सामान्य अमूर्तन किसी भी सहानुभूति सदिश स्थान से निर्मित होता है। उदाहरण के लिए, मान लीजिए (V, ω) एक परिमित-आयामी वास्तविक सिम्पलेक्टिक सदिश स्थान है (इसलिए ω V पर तिरछा सममित द्विरेखीय रूप है)। हाइजेनबर्ग समूह एच (वी) पर (वी, ω) (या संक्षिप्तता के लिए बस वी) समूह कानून के साथ संपन्न सेट वी × 'आर' है

$(v,t)\cdot \left(v',t'\right)=\left(v+v',t+t'+{\frac {1}{2}}\omega \left(v,v'\right)\right).$

हाइजेनबर्ग समूह योगात्मक समूह V का एक समूह विस्तार#केंद्रीय विस्तार है। इस प्रकार एक सटीक अनुक्रम है

$0\to \mathbf {R} \to H(V)\to V\to 0.$

कोई भी सिम्प्लेक्टिक वेक्टर स्पेस एक सिम्प्लेक्टिक वेक्टर स्पेस को स्वीकार करता है#मानक सिम्पलेक्टिक स्पेस {e_j, एफ^{कश्मीर}}_{1 ≤ j,k ≤ n} संतोषजनक ω (ई_j, एफ^{के </सुप>) = डी_jk और जहां 2n V का आयाम है (V का आयाम आवश्यक रूप से सम है)। इस आधार के संदर्भ में, प्रत्येक सदिश इस रूप में विघटित होता है}

$v=q^{a}\mathbf {e} _{a}+p_{a}\mathbf {f} ^{a}.$

एकसवाल^ए और पी_a कैनोनिक रूप से संयुग्म निर्देशांक हैं।

यदि {ई_j, एफ^{कश्मीर}}_{1 ≤ j,k ≤ n} V के लिए एक Darboux आधार है, तो {E} को 'R' के लिए एक आधार होने दें, और {'e'_j, एफ^{के</सुप>, ई}_{1 ≤ j,k ≤ n} V×'R' के लिए संगत आधार है। H(V) में एक सदिश इसके द्वारा दिया जाता है}

$v=q^{a}\mathbf {e} _{a}+p_{a}\mathbf {f} ^{a}+tE$

और समूह कानून बन जाता है

$(p,q,t)\cdot \left(p',q',t'\right)=\left(p+p',q+q',t+t'+{\frac {1}{2}}(pq'-p'q)\right).$

क्योंकि हाइजेनबर्ग समूह का अंतर्निहित कई गुना एक रेखीय स्थान है, लाई बीजगणित में वैक्टर को समूह में वैक्टर के साथ प्रामाणिक रूप से पहचाना जा सकता है। हाइजेनबर्ग समूह का लाइ बीजगणित कम्यूटेशन रिलेशन द्वारा दिया गया है

${\begin{bmatrix}(v_{1},t_{1}),(v_{2},t_{2})\end{bmatrix}}=\omega (v_{1},v_{2})$

या डार्बौक्स आधार के संदर्भ में लिखा गया है

$\left[\mathbf {e} _{a},\mathbf {f} ^{b}\right]=\delta _{a}^{b}$

और अन्य सभी कम्यूटेटर गायब हो जाते हैं।

समूह कानून को एक अलग तरीके से परिभाषित करना भी संभव है, लेकिन जो समूह को हमने अभी-अभी परिभाषित किया है, उसके लिए एक समूह समरूपता पैदा करता है। भ्रम से बचने के लिए, हम t के बजाय u का उपयोग करेंगे, इसलिए एक सदिश दिया जाता है

$v=q^{a}\mathbf {e} _{a}+p_{a}\mathbf {f} ^{a}+uE$

और समूह कानून है

$(p,q,u)\cdot \left(p',q',u'\right)=\left(p+p',q+q',u+u'+pq'\right).$

समूह का एक तत्व

$v=q^{a}\mathbf {e} _{a}+p_{a}\mathbf {f} ^{a}+uE$ फिर एक मैट्रिक्स के रूप में व्यक्त किया जा सकता है

${\begin{bmatrix}1&p&u\\0&I_{n}&q\\0&0&1\end{bmatrix}}$ ,

जो एच (वी) का एक वफादार मैट्रिक्स प्रतिनिधित्व देता है। इस फॉर्मूलेशन में यू हमारे पिछले फॉर्मूलेशन में टी से संबंधित है $u=t+{\tfrac {1}{2}}pq$, ताकि उत्पाद का t मान आ जाए

${\begin{aligned}&u+u'+pq'-{\frac {1}{2}}\left(p+p'\right)\left(q+q'\right)\\={}&t+{\frac {1}{2}}pq+t'+{\frac {1}{2}}p'q'+pq'-{\frac {1}{2}}\left(p+p'\right)\left(q+q'\right)\\={}&t+t'+{\frac {1}{2}}\left(pq'-p'q\right)\end{aligned}}$ ,

पहले जैसा।

ऊपरी त्रिकोणीय मैट्रिक्स का उपयोग करने वाले समूह के लिए आइसोमोर्फिज्म वी के अपघटन पर एक डार्बौक्स आधार पर निर्भर करता है, जो आइसोमोर्फिज्म वी ≅ यू ⊕ यू * की पसंद के बराबर होता है। हालांकि नया समूह कानून ऊपर दिए गए समूह के लिए एक समूह आइसोमोर्फिक उत्पन्न करता है, इस कानून वाले समूह को कभी-कभी 'ध्रुवीकृत हाइजेनबर्ग समूह' के रूप में संदर्भित किया जाता है, यह याद दिलाने के लिए कि यह समूह कानून आधार के विकल्प पर निर्भर करता है। V का Lagrangian उपस्थान एक एबेलियन किस्म #Polarisations है)।

किसी भी लाई बीजगणित के लिए, एक अद्वितीय कनेक्टेड स्पेस है, बस जुड़ा हुआ लाई ग्रुप जी है। जी के समान लाई बीजगणित वाले अन्य सभी जुड़े हुए लाई समूह जी / एन के रूप में हैं जहां एन जी में एक केंद्रीय असतत समूह है। इस मामले में , H(V) का केंद्र 'R' है और केवल असतत उपसमूह Z के लिए आइसोमॉर्फिक हैं। इस प्रकार H(V)/'Z' एक अन्य झूठ समूह है जो इस झूठे बीजगणित को साझा करता है। इस झूठ समूह के बारे में ध्यान देने योग्य बात यह है कि यह कोई विश्वसनीय परिमित-आयामी निरूपण स्वीकार नहीं करता है; यह किसी भी मैट्रिक्स समूह के लिए आइसोमोर्फिक नहीं है। हालाँकि इसमें अनंत-आयामी एकात्मक अभ्यावेदन का एक प्रसिद्ध परिवार है।

== वेइल बीजगणित == के साथ संबंध

Main article: Weyl algebra

झूठ बीजगणित ${\mathfrak {h}}_{n}$ हाइजेनबर्ग समूह का ऊपर वर्णित किया गया था, (1), मेट्रिसेस के झूठ बीजगणित के रूप में। पॉइनकेयर-बिरखॉफ-विट प्रमेय सार्वभौमिक लिफाफा बीजगणित निर्धारित करने के लिए लागू होता है $U({\mathfrak {h}}_{n})$. अन्य गुणों में, सार्वभौमिक आवरण बीजगणित एक साहचर्य बीजगणित है जिसमें ${\mathfrak {h}}_{n}$ इंजेक्शन से लगाया जाता है।

पोंकारे-बिरखॉफ-विट प्रमेय द्वारा, यह इस प्रकार मोनोमियल्स द्वारा उत्पन्न मुक्त मॉड्यूल है

$z^{j}p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{n}^{k_{n}}q_{1}^{\ell _{1}}q_{2}^{\ell _{2}}\cdots q_{n}^{\ell _{n}}~,$

जहां प्रतिपादक सभी गैर-नकारात्मक हैं।

फलस्वरूप, $U({\mathfrak {h}}_{n})$ वास्तविक बहुपदों से मिलकर बनता है

$\sum _{j,{\vec {k}},{\vec {\ell }}}c_{j{\vec {k}}{\vec {\ell }}}\,\,z^{j}p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{n}^{k_{n}}q_{1}^{\ell _{1}}q_{2}^{\ell _{2}}\cdots q_{n}^{\ell _{n}}~,$

रूपांतरण संबंधों के साथ

$p_{k}p_{\ell }=p_{\ell }p_{k},\quad q_{k}q_{\ell }=q_{\ell }q_{k},\quad p_{k}q_{\ell }-q_{\ell }p_{k}=\delta _{k\ell }z,\quad zp_{k}-p_{k}z=0,\quad zq_{k}-q_{k}z=0~.$

बीजगणित $U({\mathfrak {h}}_{n})$ ℝ पर डिफरेंशियल ऑपरेटर्स के बीजगणित से निकटता से संबंधित हैⁿ बहुपद गुणांकों के साथ, क्योंकि ऐसे किसी भी संकारक का रूप में अद्वितीय प्रतिनिधित्व होता है

$P=\sum _{{\vec {k}},{\vec {\ell }}}c_{{\vec {k}}{\vec {\ell }}}\,\,\partial _{x_{1}}^{k_{1}}\partial _{x_{2}}^{k_{2}}\cdots \partial _{x_{n}}^{k_{n}}x_{1}^{\ell _{1}}x_{2}^{\ell _{2}}\cdots x_{n}^{\ell _{n}}~.$

इस बीजगणित को वेइल बीजगणित कहा जाता है। अमूर्त बकवास से यह अनुसरण करता है कि वेइल बीजगणित डब्ल्यू_nका अंश है $U({\mathfrak {h}}_{n})$. हालाँकि, यह उपरोक्त अभ्यावेदन से सीधे देखना भी आसान है; अर्थात मैपिंग द्वारा

$z^{j}p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{n}^{k_{n}}q_{1}^{\ell _{1}}q_{2}^{\ell _{2}}\cdots q_{n}^{\ell _{n}}\,\mapsto \,\partial _{x_{1}}^{k_{1}}\partial _{x_{2}}^{k_{2}}\cdots \partial _{x_{n}}^{k_{n}}x_{1}^{\ell _{1}}x_{2}^{\ell _{2}}\cdots x_{n}^{\ell _{n}}~.$

अनुप्रयोग

क्वांटम यांत्रिकी का वेइल का मानकीकरण

Main article: Wigner–Weyl transform

हाइजेनबर्ग समूह के एक स्पष्ट अहसास के लिए हरमन वेइल का नेतृत्व करने वाला आवेदन यह सवाल था कि श्रोडिंगर तस्वीर और हाइजेनबर्ग तस्वीर भौतिक रूप से समकक्ष क्यों हैं। संक्षेप में, इसका कारण स्टोन-वॉन न्यूमैन प्रमेय है: केंद्रीय लाई बीजगणित तत्व z की दी गई क्रिया के साथ एक अद्वितीय एकात्मक प्रतिनिधित्व है, एकात्मक तुल्यता तक: बीजगणित के गैर-तुच्छ तत्व सामान्य स्थिति और गति के बराबर हैं ऑपरेटरों।

इस प्रकार, श्रोडिंगर चित्र और हाइजेनबर्ग चित्र समतुल्य हैं - वे इस अनिवार्य रूप से अद्वितीय प्रतिनिधित्व को साकार करने के अलग-अलग तरीके हैं।

थीटा प्रतिनिधित्व

Main article: theta representation

एबेलियन किस्मों को परिभाषित करने वाले समीकरणों के अपने सिद्धांत में असतत हाइजेनबर्ग समूहों के लिए डेविड ममफोर्ड द्वारा समान विशिष्टता परिणाम का उपयोग किया गया था। यह जैकोबी के अण्डाकार कार्यों में उपयोग किए जाने वाले दृष्टिकोण का एक बड़ा सामान्यीकरण है, जो मोडुलो 2 हाइजेनबर्ग समूह का मामला है, क्रम 8 का। सबसे सरल मामला हाइजेनबर्ग समूह का थीटा प्रतिनिधित्व है, जिसमें से असतत मामला थीटा फ़ंक्शन देता है। .

फूरियर विश्लेषण

हाइजेनबर्ग समूह फूरियर विश्लेषण में भी होता है, जहां इसका उपयोग स्टोन-वॉन न्यूमैन प्रमेय के कुछ योगों में किया जाता है। इस मामले में, हाइजेनबर्ग समूह को वर्ग समाकलनीय कार्यों के स्थान पर कार्य करने के लिए समझा जा सकता है; परिणाम हाइजेनबर्ग समूहों का प्रतिनिधित्व है जिसे कभी-कभी वेइल प्रतिनिधित्व कहा जाता है।

== उप-रिमानियन मैनिफोल्ड == के रूप में

हाइजेनबर्ग समूह में एक जियोडेसिक का एनिमेशन।

त्रि-आयामी हाइजेनबर्ग समूह एच₃(आर) वास्तविक पर भी एक चिकनी कई गुना समझा जा सकता है, और विशेष रूप से, उप-रिमेंनियन कई गुना का एक सरल उदाहरण। 'R' में एक बिंदु p=(x,y,z) दिया गया है³, इस बिंदु पर एक अंतर 1-रूप Θ परिभाषित करें

$\Theta _{p}=dz-{\frac {1}{2}}\left(xdy-ydx\right).$

यह एक-रूप R के स्पर्शरेखा बंडल से संबंधित है³; वह है,

$\Theta _{p}:T_{p}\mathbf {R} ^{3}\to \mathbf {R}$

स्पर्शरेखा बंडल पर एक नक्शा है। होने देना

$H_{p}=\left\{v\in T_{p}\mathbf {R} ^{3}\mid \Theta _{p}(v)=0\right\}.$

यह देखा जा सकता है कि H स्पर्शरेखा उपबंडल T'R' का एक उपसमूह है^{3</उप>। एक्स और वाई दिशा में वैक्टर द्वारा फैले द्वि-आयामी अंतरिक्ष में वैक्टर को प्रोजेक्ट करके एच पर एक कोमेट दिया जाता है। यानी दिए गए वैक्टर $v=(v_{1},v_{2},v_{3})$ और $w=(w_{1},w_{2},w_{3})$ टीआर में3, आंतरिक उत्पाद द्वारा दिया गया है}

$\langle v,w\rangle =v_{1}w_{1}+v_{2}w_{2}.$

परिणामी संरचना एच को हाइजेनबर्ग समूह के कई गुना में बदल देती है। मैनिफोल्ड पर एक ऑर्थोनॉर्मल फ्रेम लाइ वेक्टर क्षेत्र ्स द्वारा दिया गया है

${\begin{aligned}X&={\frac {\partial }{\partial x}}-{\frac {1}{2}}y{\frac {\partial }{\partial z}},\\Y&={\frac {\partial }{\partial y}}+{\frac {1}{2}}x{\frac {\partial }{\partial z}},\\Z&={\frac {\partial }{\partial z}},\end{aligned}}$

जो संबंधों [X, Y] = Z और [X, Z] = [Y, Z] = 0 का पालन करते हैं। सदिश क्षेत्र होने के नाते, ये समूह कार्रवाई के लिए एक बाएं-अपरिवर्तनीय आधार बनाते हैं। मैनिफोल्ड पर geodesic ्स सर्पिल हैं, जो दो आयामों में मंडलियों के नीचे पेश करते हैं। यानी अगर

$\gamma (t)=(x(t),y(t),z(t))$

एक जियोडेसिक वक्र है, फिर वक्र $c(t)=(x(t),y(t))$ एक वृत्त का चाप है, और

$z(t)={\frac {1}{2}}\int _{c}xdy-ydx$

दो-आयामी विमान तक सीमित अभिन्न अंग के साथ। अर्थात्, वक्र की ऊँचाई वृत्ताकार चाप द्वारा अंतरित वृत्त के क्षेत्रफल के समानुपाती होती है, जो स्टोक्स के प्रमेय के अनुसार होती है।

एक स्थानीय रूप से कॉम्पैक्ट एबेलियन समूह का हाइजेनबर्ग समूह

स्थानीय रूप से कॉम्पैक्ट एबेलियन समूह K के हाइजेनबर्ग समूह को परिभाषित करना आम तौर पर अधिक संभव है, जो हार माप से सुसज्जित है। इस तरह के एक समूह में पोंट्रजगिन दोहरी है ${\hat {K}}$, सभी निरंतर से मिलकर $U(1)$K पर मूल्यवान वर्ण, जो कॉम्पैक्ट-ओपन टोपोलॉजी के साथ संपन्न होने पर स्थानीय रूप से कॉम्पैक्ट एबेलियन समूह भी है। स्थानीय रूप से कॉम्पैक्ट एबेलियन समूह K से जुड़ा हाइजेनबर्ग समूह एकात्मक समूह का उपसमूह है $L^{2}(K)$ K से अनुवाद द्वारा उत्पन्न और के तत्वों द्वारा गुणन ${\hat {K}}$.

अधिक विस्तार से, हिल्बर्ट अंतरिक्ष $L^{2}(K)$ स्क्वायर-इंटीग्रेबल कॉम्प्लेक्स-वैल्यू फ़ंक्शंस शामिल हैं $f$ K पर। K में अनुवाद K पर ऑपरेटरों के रूप में K का एकात्मक प्रतिनिधित्व करता है $L^{2}(K)$:

$(T_{x}f)(y)=f(x+y)$

के लिए $x,y\in K$. इसलिए वर्णों द्वारा गुणन भी करें:

$(M_{\chi }f)(y)=\chi (y)f(y)$

के लिए $\chi \in {\hat {K}}$. ये ऑपरेटर कम्यूट नहीं करते, बल्कि संतुष्ट रहते हैं

$\left(T_{x}M_{\chi }T_{x}^{-1}M_{\chi }^{-1}f\right)(y)={\overline {\chi (x)}}f(y)$

एक निश्चित इकाई मापांक जटिल संख्या से गुणा।

तो हाइजेनबर्ग समूह $H(K)$ K से जुड़ा एक प्रकार का केंद्रीय विस्तार (गणित) है $K\times {\hat {K}}$, समूहों के एक सटीक अनुक्रम के माध्यम से:

$1\to U(1)\to H(K)\to K\times {\hat {K}}\to 0.$

समूह कोहोलॉजी में अधिक सामान्य हाइजेनबर्ग समूहों को 2-cocyles द्वारा वर्णित किया गया है $H^{2}(K,U(1))$. के बीच एक द्वैत का अस्तित्व $K$ और ${\hat {K}}$ एक कैनोनिकल कोसायकल को जन्म देता है, लेकिन आम तौर पर अन्य भी होते हैं।

हाइजेनबर्ग समूह अलघुकरणीय रूप से कार्य करता है $L^{2}(K)$. दरअसल, निरंतर वर्ण अलग-अलग बिंदु हैं तो कोई भी एकात्मक संचालिका $L^{2}(K)$ जो उनके साथ यात्रा करता है वह एक है $L^{\infty }$ फूरियर गुणक। लेकिन अनुवाद के साथ आने का तात्पर्य है कि गुणक स्थिर है। जॉर्ज मैके द्वारा सिद्ध स्टोन-वॉन न्यूमैन प्रमेय का एक संस्करण हाइजेनबर्ग समूह के लिए मान्य है $H(K)$. फूरियर रूपांतरण के अभ्यावेदन के बीच अद्वितीय इंटरविनर है $L^{2}(K)$ और $L^{2}\left({\hat {K}}\right)$. विवरण के लिए स्टोन–वॉन न्यूमैन प्रमेय#रिलेशन टू द फूरियर रूपांतरण पर चर्चा देखें।

यह भी देखें

• कैनोनिकल कम्यूटेशन संबंध
• विग्नर-वेइल रूपांतरण
• स्टोन-वॉन न्यूमैन प्रमेय
• अनुमानित प्रतिनिधित्व

संदर्भ

• Binz, Ernst; Pods, Sonja (2008). Geometry of Heisenberg Groups. American Mathematical Society. ISBN 978-0-8218-4495-3.
• Hall, Brian C. (2013), Quantum Theory for Mathematicians, Graduate Texts in Mathematics, vol. 267, Springer, ISBN 978-1461471158
• Hall, Brian C. (2015). Lie Groups, Lie Algebras, and Representations: An Elementary Introduction. Graduate Texts in Mathematics. Vol. 222 (second ed.). Springer. ISBN 978-3319134666.
• Howe, Roger (1980). "On the role of the Heisenberg group in harmonic analysis". Bulletin of the American Mathematical Society. 3 (2): 821–843. doi:10.1090/s0273-0979-1980-14825-9. MR 0578375.
• Kirillov, Alexandre A. (2004). "Ch. 2: "Representations and Orbits of the Heisenberg Group". Lectures on the Orbit Method. American Mathematical Society. ISBN 0-8218-3530-0.
• Mackey, George (1976). The theory of Unitary Group Representations. Chicago Lectures in Mathematics. University of Chicago Press. ISBN 978-0226500522.

बाहरी संबंध

• Groupprops, The Group Properties Wiki Unitriangular matrix group UT(3,p)