Difference between revisions of "सातत्य समीकरण"
(Created page with "{{Short description|Equation describing the transport of some quantity}} {{continuum mechanics}} एक निरंतरता समीकरण या परिवह...") |
Radhamishra (talk | contribs) |
||
| Line 2: | Line 2: | ||
{{continuum mechanics}} | {{continuum mechanics}} | ||
सांतत्य समीकरण या अभिगमन समीकरण एक समीकरण है जो कुछ राशि के अभिगमन का वर्णन करता है। संरक्षित राशि पर प्रयुक्त होने पर यह विशेष रूप से सरल और प्रभावशाली होता है, लेकिन इसे किसी भी व्यापक राशि पर प्रयुक्त करने के लिए सामान्यीकृत किया जा सकता है। चूँकि द्रव्यमान, ऊर्जा, संवेग, विद्युत आवेश और अन्य प्राकृतिक राशि उनकी संबंधित उपयुक्त परिस्थितियों में संरक्षित होती हैं, इसलिए सांतत्य समीकरणों का उपयोग करके विभिन्न प्रकार की भौतिक घटनाओं का वर्णन किया जा सकता है। | |||
सांतत्य समीकरण [[संरक्षण कानून (भौतिकी)|संरक्षण नियम (भौतिकी)]] का एक प्रबल, स्थानीय रूप है। उदाहरण के लिए, ऊर्जा संरक्षण के नियम का एक दुर्बल संस्करण बताता है कि ऊर्जा को न तो बनाया जा सकता है और न ही नष्ट किया जा सकता है - अर्थात, ब्रह्मांड में ऊर्जा की कुल राशि निश्चित है। यह कथन इस संभावना से अस्वीकृत नहीं करता है कि ऊर्जा की एक राशि एक बिंदु से नष्ट हो सकती है जबकि एक साथ दूसरे बिंदु पर दिखाई दे सकती है। एक प्रबल कथन यह है कि ऊर्जा स्थानीय रूप से संरक्षित होती है: ऊर्जा को न तो बनाया जा सकता है और न ही नष्ट किया जा सकता है, न ही इसे एक स्थान से दूसरे स्थान पर "स्थानांतरण" किया जा सकता है - यह केवल निरंतर अभिवाह (फ्लक्स) द्वारा स्थानांतरित हो सकती है। सांतत्य समीकरण इस प्रकार के कथन को व्यक्त करने का गणितीय तरीका है। उदाहरण के लिए, विद्युत आवेश के लिए सांतत्य समीकरण बताता है कि स्थान के किसी भी आयतन में विद्युत आवेश की मात्रा केवल उस आयतन की सीमाओं के माध्यम से उसके अंदर या बाहर प्रवाहित होने वाली विद्युत धारा की राशि से बदल सकती है। | |||
सांतत्य समीकरणों में सामान्य रूप से स्रोत और मंद शब्द सम्मिलित हो सकते हैं, जो उन्हें उन राशियों का वर्णन करने की अनुमति देते हैं जो प्रायः होती हैं लेकिन सदैव संरक्षित नहीं होती हैं, जैसे आणविक प्रजातियों का घनत्व जो रासायनिक प्रतिक्रियाओं द्वारा बनाया या नष्ट किया जा सकता है। दैनिक जीवन के उदाहरण में, जीवित लोगों की संख्या के लिए एक सांतत्य समीकरण है; इसमें जन्म लेने वाले लोगों के लिए एक स्रोत शब्द है, और मरने वाले लोगों के लिए एक मंद शब्द है। | |||
किकिसी भी सांतत्य समीकरण को "समाकल रूप" (अभिवाह समाकल के संदर्भ में) में व्यक्त किया जा सकता है, जो किसी भी परिमित क्षेत्र पर प्रयुक्त होता है, या "अवकल रूप" (विचलन संचालिका के संदर्भ में) में व्यक्त किया जा सकता है जो एक बिंदु पर प्रयुक्त होता है। | |||
सांतत्य समीकरण अधिक विशिष्ट अभिगमन समीकरणों जैसे कि संवहन-प्रसार समीकरण, बोल्ट्ज़मैन अभिगमन समीकरण और नेवियर-स्टोक्स समीकरणों के अंतर्गत आते हैं। | |||
सांतत्य समीकरणों द्वारा नियंत्रित अभिवाह को सैंकी आरेख का उपयोग करके देखा जा सकता है। | |||
== सामान्य समीकरण == | == सामान्य समीकरण == | ||
=== | === अभिवाह की परिभाषा === | ||
{{main| | {{main|प्रवाह}} | ||
जब अभिवाह को परिभाषित किया जा सकता है तो सांतत्य समीकरण उपयोगी होता है। अभिवाह को परिभाषित करने के लिए सबसे पहले एक मात्रा q होनी चाहिए जो प्रवाहित या गति कर सके, जैसे द्रव्यमान, ऊर्जा, विद्युत आवेश, संवेग, अणुओं की संख्या, आदि सम्मिलित है। मान लीजिए ρ इस राशि का आयतन घनत्व है जो प्रति इकाई आयतन q की मात्रा है। | |||
जिस तरह से यह मात्रा | जिस तरह से यह मात्रा q प्रवाहित हो रही है उसका वर्णन इसके अभिवाह द्वारा किया जाता है। q का अभिवाह एक सदिश क्षेत्र है, जिसे हम j के रूप में दर्शाते हैं। यहां अभिवाह के कुछ उदाहरण और गुण दिए गए हैं: | ||
* | * अभिवाह का आयाम "एक इकाई क्षेत्र के माध्यम से प्रति इकाई समय में प्रवाहित q की मात्रा" है। उदाहरण के लिए, प्रवाहित पानी के लिए द्रव्यमान सांतत्य समीकरण में, यदि 1 cm<sup>2</sup> प्रतिनिध्यात्मक क्षेत्र वाले पाइप के माध्यम से 1 ग्राम प्रति सेकंड पानी प्रवाहित हो रहा है, तो पाइप के अंदर औसत द्रव्यमान अभिवाह '''j''' (1 g/s)/cm<sup>2</sup> है। और इसकी दिशा पाइप के साथ उस दिशा में होती है जिस दिशा में पानी प्रवाहित हो रहा है। पाइप के बाहर, जहां पानी नहीं है, अभिवाह शून्य है। | ||
* यदि कोई | *यदि कोई वेग क्षेत्र '''u''' है जो प्रासंगिक अभिवाह का वर्णन करता है - दूसरे शब्दों में, यदि बिंदु '''x''' पर सभी मात्रा q वेग '''u(x)''' के साथ घूम रही है - तो परिभाषा के अनुसार अभिवाह वेग क्षेत्र के घनत्व गुना के बराबर है : | ||
: <math display="block">\mathbf{j} = \rho \mathbf{u}</math> | : <math display="block">\mathbf{j} = \rho \mathbf{u}</math> | ||
: उदाहरण के लिए, यदि | : उदाहरण के लिए, यदि प्रवाहित पानी के द्रव्यमान सांतत्य समीकरण में, {{math|'''u'''}} प्रत्येक बिंदु पर पानी का वेग है, और {{math|''ρ''}} प्रत्येक बिंदु पर पानी का घनत्व है, तब {{math|'''j'''}} द्रव्यमान अभिवाह होगा। | ||
* एक | * एक प्रचलित उदाहरण में, विद्युत आवेश का अभिवाह [[विद्युत प्रवाह घनत्व|विद्युत अभिवाह घनत्व]] है। | ||
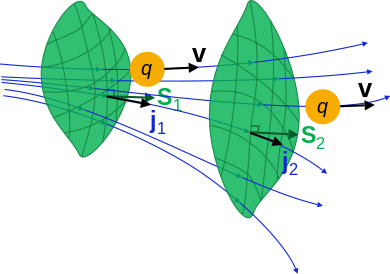
[[File:Continuity eqn open surface.svg|390px|right|thumb| | [[File:Continuity eqn open surface.svg|390px|right|thumb|एक मात्रा q का अभिवाह '''j''' एक विवृत सतह S से कैसे गुजरता है इसका (''d'''''S''' अवकल सदिश क्षेत्र है) चित्रण है।]] | ||
* यदि कोई काल्पनिक सतह S है, तो S पर अभिवाह का सतह समाकल q की मात्रा के बराबर है जो प्रति इकाई समय में सतह S से गुजर रहा है: | |||
{{Equation box 1 | {{Equation box 1 | ||
|indent=: | |indent=: | ||
| Line 36: | Line 38: | ||
|background colour = #ECFCF4 | |background colour = #ECFCF4 | ||
}} | }} | ||
: जिसमें <math display="inline">\iint_S d\mathbf{S}</math> एक सतह | : जिसमें <math display="inline">\iint_S d\mathbf{S}</math> एक सतह समाकल है। | ||
ध्यान दें कि जिस अवधारणा को यहां <nowiki>''अभिवाह'' कहा गया है, उसे कुछ साहित्य में वैकल्पिक रूप से "अभिवाह घनत्व" कहा जाता है, जिसके संदर्भ में ''अभिवाह''</nowiki> या अभिवाह घनत्व के सतह समाकल को दर्शाता है। विवरण के लिए अभिवाह पर मुख्य लेख देखें। | |||
=== | ===समाकल रूप === | ||
सांतत्य समीकरण का समाकल रूप बताता है कि: | |||
* | * किसी क्षेत्र में q की मात्रा तब बढ़ती है जब अतिरिक्त q क्षेत्र की सतह से अंदर की ओर प्रवाहित है, और जब यह बाहर की ओर प्रवाहित है तो घट जाती है; | ||
* | * किसी क्षेत्र में q की मात्रा तब बढ़ती है जब क्षेत्र के अंदर नया q बनाया जाता है, और q नष्ट होने पर घट जाती है; | ||
*इन | *इन दो प्रक्रियाओं के अतिरिक्त, किसी क्षेत्र में q की मात्रा को बदलने का कोई अन्य तरीका नहीं है। | ||
गणितीय रूप से, | गणितीय रूप से, आयतन V के अंदर q की वृद्धि की दर को व्यक्त करने वाले सांतत्य समीकरण का समाकल रूप है: | ||
{{Equation box 1 | {{Equation box 1 | ||
|indent=: | |indent=: | ||
| Line 57: | Line 59: | ||
}} | }} | ||
[[File:SurfacesWithAndWithoutBoundary.svg|right|thumb|250px| | [[File:SurfacesWithAndWithoutBoundary.svg|right|thumb|250px|सांतत्य समीकरण के समाकल रूप में, {{math|''S''}} कोई भी [[बंद सतह|संवृत सतह]] है जो पूरी तरह से राशि {{math|''V''}} बाईं ओर की किसी भी सतह को घेरती है। {{math|''S''}} सीमाओं वाली सतह नहीं हो सकती, जैसे कि दाईं ओरस्थित है। (सतहें नीली हैं, सीमाएँ लाल हैं।)]]जहां | ||
* | * S कोई काल्पनिक संवृत सतह है, जो आयतन V को घेरती है, | ||
* {{oiint | preintegral = | intsubscpt = {{math|''S''}} | integrand={{math|''d'''''S'''}}}} उस | * {{oiint | preintegral = | intsubscpt = {{math|''S''}} | integrand={{math|''d'''''S'''}}}} उस संवृत सतह पर सतह समाकल को दर्शाता है, | ||
* | * q आयतन V में मात्रा की कुल राशि है, | ||
* {{math|'''j'''}} | * {{math|'''j'''}}, {{math|''q''}} का प्रवाह है | ||
* {{math|''t''}} | * {{math|''t''}} समय है, '''edit''' | ||
* {{math|Σ}} शुद्ध दर है कि {{math|''q''}} वॉल्यूम के अंदर उत्पन्न हो रहा है {{math|''V''}} प्रति यूनिट समय। कब {{math|''q''}} उत्पन्न हो रहा है, इसे का स्रोत कहते हैं {{math|''q''}}, और यह बनाता है {{math|Σ}} अधिक सकारात्मक। कब {{math|''q''}} नष्ट हो रहा है, इसे | * {{math|Σ}} शुद्ध दर है कि {{math|''q''}} वॉल्यूम के अंदर उत्पन्न हो रहा है {{math|''V''}} प्रति यूनिट समय। कब {{math|''q''}} उत्पन्न हो रहा है, इसे का स्रोत कहते हैं {{math|''q''}}, और यह बनाता है {{math|Σ}} अधिक सकारात्मक। कब {{math|''q''}} नष्ट हो रहा है, इसे मंद कहा जाता है {{math|''q''}}, और यह बनाता है {{math|Σ}} अधिक नकारात्मक। यह शब्द कभी-कभी लिखा जाता है <math>dq/dt|_\text{gen}</math> या नियंत्रण आयतन के अंदर इसकी उत्पत्ति या विनाश से क्यू का कुल परिवर्तन। | ||
एक साधारण उदाहरण में, {{math|''V''}} एक इमारत हो सकती है, और {{math|''q''}} इमारत में लोगों की संख्या हो सकती है। सतह {{math|''S''}} में भवन की दीवारें, दरवाजे, छत और नींव | एक साधारण उदाहरण में, {{math|''V''}} एक इमारत हो सकती है, और {{math|''q''}} इमारत में लोगों की संख्या हो सकती है। सतह {{math|''S''}} में भवन की दीवारें, दरवाजे, छत और नींव सम्मिलित होगी। फिर सांतत्य समीकरण बताता है कि जब लोग इमारत में प्रवेश करते हैं तो लोगों की संख्या बढ़ जाती है (सतह के माध्यम से एक आवक प्रवाह), जब लोग इमारत से बाहर निकलते हैं (सतह के माध्यम से एक बाहरी प्रवाह), घट जाती है जब इमारत में कोई व्यक्ति देता है जन्म (एक स्रोत, {{math|Σ > 0}}), और घटता है जब इमारत में किसी की मृत्यु हो जाती है (एक मंद, {{math|Σ < 0}}). | ||
=== | === अवकल रूप === | ||
{{see also|Conservation law|conservation form}} | {{see also|Conservation law|conservation form}} | ||
[[विचलन प्रमेय]] द्वारा, एक सामान्य | [[विचलन प्रमेय]] द्वारा, एक सामान्य सांतत्य समीकरण को अंतर रूप में भी लिखा जा सकता है: | ||
{{Equation box 1 | {{Equation box 1 | ||
|indent=: | |indent=: | ||
| Line 80: | Line 82: | ||
कहाँ | कहाँ | ||
* {{math|∇⋅}} विचलन है, | * {{math|∇⋅}} विचलन है, | ||
* {{math|''ρ''}} | * {{math|''ρ''}} राशि की राशि है {{math|''q''}} प्रति इकाई आयतन, | ||
* {{math|'''j'''}} का | * {{math|'''j'''}} का अभिवाह घनत्व है {{math|''q''}}, | ||
* {{math|''t''}} यह समय है, | * {{math|''t''}} यह समय है, | ||
* {{math|''σ''}} की पीढ़ी है {{math|''q''}} प्रति इकाई आयतन प्रति इकाई समय। उत्पन्न करने वाली शर्तें {{math|''q''}} (अर्थात।, {{math|''σ'' > 0}}) या हटा दें {{math|''q''}} (अर्थात।, {{math|''σ'' < 0}}) को क्रमशः स्रोत और | * {{math|''σ''}} की पीढ़ी है {{math|''q''}} प्रति इकाई आयतन प्रति इकाई समय। उत्पन्न करने वाली शर्तें {{math|''q''}} (अर्थात।, {{math|''σ'' > 0}}) या हटा दें {{math|''q''}} (अर्थात।, {{math|''σ'' < 0}}) को क्रमशः स्रोत और मंद कहा जाता है। | ||
इस सामान्य समीकरण का उपयोग किसी भी | इस सामान्य समीकरण का उपयोग किसी भी सांतत्य समीकरण को प्राप्त करने के लिए किया जा सकता है, जो वॉल्यूम सांतत्य समीकरण के रूप में सरल से लेकर नेवियर-स्टोक्स समीकरण के रूप में जटिल है। यह समीकरण [[संवहन समीकरण]] का भी सामान्यीकरण करता है। भौतिकी में अन्य समीकरण, जैसे कि गॉस का नियम | विद्युत क्षेत्र का गॉस का नियम और गुरुत्वाकर्षण के लिए गॉस का नियम, सांतत्य समीकरण के समान गणितीय रूप है, लेकिन सामान्य रूप से शब्द सांतत्य समीकरण द्वारा संदर्भित नहीं किया जाता है, क्योंकि {{math|'''j'''}} उन मामलों में वास्तविक भौतिक राशि के अभिवाह का प्रतिनिधित्व नहीं करता है। | ||
उस मामले में {{math|''q''}} एक संरक्षण | उस मामले में {{math|''q''}} एक संरक्षण नियम (भौतिकी) है जिसे बनाया या नष्ट नहीं किया जा सकता (जैसे ऊर्जा), {{math|1=''σ'' = 0}} और समीकरण बन जाते हैं: | ||
<math display="block">\frac{\partial \rho}{\partial t} + \nabla \cdot \mathbf{j} = 0</math> | <math display="block">\frac{\partial \rho}{\partial t} + \nabla \cdot \mathbf{j} = 0</math> | ||
| Line 95: | Line 97: | ||
{{Main|Charge conservation}} | {{Main|Charge conservation}} | ||
[[विद्युत चुम्बकीय सिद्धांत]] में, | [[विद्युत चुम्बकीय सिद्धांत]] में, सांतत्य समीकरण एक अनुभवजन्य नियम है जो [[चार्ज संरक्षण]] (स्थानीय) व्यक्त करता है। गणितीय रूप से यह मैक्सवेल के समीकरणों का स्वत: परिणाम है, हालांकि चार्ज संरक्षण मैक्सवेल के समीकरणों की तुलना में अधिक मौलिक है। यह बताता है कि [[वर्तमान घनत्व]] का विचलन {{math|'''J'''}} ([[एम्पीयर]] प्रति वर्ग मीटर में) आवेश घनत्व के परिवर्तन की ऋणात्मक दर के बराबर है {{math|''ρ''}} ([[कूलम्ब]] प्रति घन मीटर में), | ||
<math display="block"> \nabla \cdot \mathbf{J} = - \frac{\partial \rho}{\partial t} </math> | <math display="block"> \nabla \cdot \mathbf{J} = - \frac{\partial \rho}{\partial t} </math> | ||
| Line 113: | Line 115: | ||
}} | }} | ||
करंट आवेश की गति है। | करंट आवेश की गति है। सांतत्य समीकरण कहता है कि यदि आवेश एक अवकल आयतन से बाहर निकल रहा है (अर्थात, वर्तमान घनत्व का विचलन धनात्मक है) तो उस आयतन के भीतर आवेश की मात्रा घटने वाली है, इसलिए आवेश घनत्व के परिवर्तन की दर ऋणात्मक है। इसलिए, सांतत्य समीकरण आवेश के संरक्षण के बराबर है। | ||
यदि [[चुंबकीय मोनोपोल]] मौजूद हैं, तो मोनोपोल धाराओं के लिए | यदि [[चुंबकीय मोनोपोल]] मौजूद हैं, तो मोनोपोल धाराओं के लिए सांतत्य समीकरण भी होगा, पृष्ठभूमि के लिए मोनोपोल आलेख और विद्युत और चुंबकीय धाराओं के बीच द्वंद्व देखें। | ||
== द्रव गतिकी == | == द्रव गतिकी == | ||
| Line 121: | Line 123: | ||
{{see also|Mass flux|Mass flow rate|Vorticity equation}} | {{see also|Mass flux|Mass flow rate|Vorticity equation}} | ||
द्रव गतिकी में, | द्रव गतिकी में, सांतत्य समीकरण बताता है कि जिस दर पर द्रव्यमान एक प्रणाली में प्रवेश करता है वह उस दर के बराबर होता है जिस पर द्रव्यमान प्रणाली को छोड़ देता है और साथ ही प्रणाली के भीतर द्रव्यमान का संचय होता है।<ref name=Pedlosky>{{Cite book | publisher = [[Springer Science+Business Media|Springer]] | isbn = 978-0-387-96387-7 | last = Pedlosky | first = Joseph | title = भूभौतिकीय द्रव गतिकी| year = 1987 | pages = [https://archive.org/details/geophysicalfluid00jose/page/10 10–13] | url = https://archive.org/details/geophysicalfluid00jose/page/10 }}</ref><ref>Clancy, L.J.(1975), ''Aerodynamics'', Section 3.3, Pitman Publishing Limited, London</ref> | ||
सांतत्य समीकरण का अंतर रूप है:<ref name=Pedlosky/> | |||
<math display="block"> \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{u}) = 0</math> | <math display="block"> \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{u}) = 0</math> | ||
कहाँ | कहाँ | ||
* {{math|''ρ''}} द्रव घनत्व है, | * {{math|''ρ''}} द्रव घनत्व है, | ||
* {{math|''t''}} यह समय है, | * {{math|''t''}} यह समय है, | ||
* {{math|'''u'''}} [[प्रवाह वेग]] सदिश क्षेत्र है। | * {{math|'''u'''}} [[प्रवाह वेग|अभिवाह वेग]] सदिश क्षेत्र है। | ||
समय व्युत्पन्न को प्रणाली में द्रव्यमान के संचय (या हानि) के रूप में समझा जा सकता है, जबकि विचलन शब्द | समय व्युत्पन्न को प्रणाली में द्रव्यमान के संचय (या हानि) के रूप में समझा जा सकता है, जबकि विचलन शब्द अभिवाह बनाम अभिवाह में अंतर का प्रतिनिधित्व करता है। इस संदर्भ में, यह समीकरण भी यूलर समीकरणों (द्रव गतिकी) में से एक है। नेवियर-स्टोक्स समीकरण रैखिक गति के संरक्षण का वर्णन करते हुए एक सदिश सांतत्य समीकरण बनाते हैं। | ||
यदि तरल [[असंपीड्य प्रवाह]] है (वॉल्यूमेट्रिक तनाव दर शून्य है), द्रव्यमान | यदि तरल [[असंपीड्य प्रवाह|असंपीड्य]] अभिवाह है (वॉल्यूमेट्रिक तनाव दर शून्य है), द्रव्यमान सांतत्य समीकरण वॉल्यूम सांतत्य समीकरण को सरल बनाता है:<ref name="Fielding">{{cite web |last1=Fielding |first1=Suzanne |title=द्रव गतिकी की मूल बातें|url=https://community.dur.ac.uk/suzanne.fielding/teaching/BLT/sec1.pdf |website=Durham University |access-date=22 December 2019}}</ref> | ||
<math display="block">\nabla \cdot \mathbf{u} = 0,</math> | <math display="block">\nabla \cdot \mathbf{u} = 0,</math> | ||
जिसका अर्थ है कि वेग क्षेत्र का विचलन हर जगह शून्य है। शारीरिक रूप से, यह कहने के बराबर है कि स्थानीय आयतन फैलाव दर शून्य है, इसलिए एक अभिसरण पाइप के माध्यम से पानी का | जिसका अर्थ है कि वेग क्षेत्र का विचलन हर जगह शून्य है। शारीरिक रूप से, यह कहने के बराबर है कि स्थानीय आयतन फैलाव दर शून्य है, इसलिए एक अभिसरण पाइप के माध्यम से पानी का अभिवाह पूरी तरह से इसके वेग को बढ़ाकर समायोजित करेगा क्योंकि पानी काफी हद तक असम्पीडित है। | ||
== कंप्यूटर दृष्टि == | == कंप्यूटर दृष्टि == | ||
| Line 139: | Line 141: | ||
{{Main|Optical flow}} | {{Main|Optical flow}} | ||
[[कंप्यूटर दृष्टि]] में, ऑप्टिकल | [[कंप्यूटर दृष्टि]] में, ऑप्टिकल अभिवाह दृश्य दृश्य में वस्तुओं की स्पष्ट गति का पैटर्न है। इस धारणा के तहत कि गतिमान वस्तु की चमक दो छवि फ़्रेमों के बीच नहीं बदली, कोई ऑप्टिकल अभिवाह समीकरण को इस प्रकार प्राप्त कर सकता है: | ||
<math display="block">\frac{\partial I}{\partial x}V_x + \frac{\partial I}{\partial y}V_y + \frac{\partial I}{\partial t} | <math display="block">\frac{\partial I}{\partial x}V_x + \frac{\partial I}{\partial y}V_y + \frac{\partial I}{\partial t} | ||
= \nabla I\cdot\mathbf{V} + \frac{\partial I}{\partial t} | = \nabla I\cdot\mathbf{V} + \frac{\partial I}{\partial t} | ||
| Line 147: | Line 149: | ||
* {{math|''x'', ''y''}} छवि में निर्देशांक करता है, | * {{math|''x'', ''y''}} छवि में निर्देशांक करता है, | ||
* {{math|''I''}} छवि निर्देशांक पर छवि तीव्रता है {{math|(''x'', ''y'')}} और समय {{mvar|t}}, | * {{math|''I''}} छवि निर्देशांक पर छवि तीव्रता है {{math|(''x'', ''y'')}} और समय {{mvar|t}}, | ||
* {{math|'''V'''}} ऑप्टिकल | * {{math|'''V'''}} ऑप्टिकल अभिवाह वेग सदिश है <math>(V_x, V_y)</math> छवि समन्वय पर {{math|(''x'', ''y'')}} और समय {{mvar|t}} | ||
== ऊर्जा और ताप == | == ऊर्जा और ताप == | ||
ऊर्जा का संरक्षण कहता है कि ऊर्जा को न तो बनाया जा सकता है और न ही नष्ट किया जा सकता है। (सामान्य सापेक्षता से जुड़ी बारीकियों के लिए #सामान्य सापेक्षता देखें।) इसलिए, ऊर्जा | ऊर्जा का संरक्षण कहता है कि ऊर्जा को न तो बनाया जा सकता है और न ही नष्ट किया जा सकता है। (सामान्य सापेक्षता से जुड़ी बारीकियों के लिए #सामान्य सापेक्षता देखें।) इसलिए, ऊर्जा अभिवाह के लिए एक सांतत्य समीकरण है: | ||
<math display="block">\frac{ \partial u}{\partial t} + \nabla \cdot \mathbf{q} = 0</math> | <math display="block">\frac{ \partial u}{\partial t} + \nabla \cdot \mathbf{q} = 0</math> | ||
कहाँ | कहाँ | ||
* {{math|''u''}}, स्थानीय [[ऊर्जा घनत्व]] (ऊर्जा प्रति इकाई आयतन), | * {{math|''u''}}, स्थानीय [[ऊर्जा घनत्व]] (ऊर्जा प्रति इकाई आयतन), | ||
* {{math|'''q'''}}, एक | * {{math|'''q'''}}, एक सदिश के रूप में [[ऊर्जा प्रवाह|ऊर्जा]] अभिवाह (प्रति यूनिट क्रॉस-अनुभागीय क्षेत्र प्रति यूनिट समय में ऊर्जा का हस्तांतरण), | ||
एक महत्वपूर्ण व्यावहारिक उदाहरण [[ गर्मी का हस्तांतरण ]] है। जब गर्मी एक ठोस के अंदर प्रवाहित होती है, तो ऊष्मा समीकरण पर पहुंचने के लिए | एक महत्वपूर्ण व्यावहारिक उदाहरण [[ गर्मी का हस्तांतरण ]] है। जब गर्मी एक ठोस के अंदर प्रवाहित होती है, तो ऊष्मा समीकरण पर पहुंचने के लिए सांतत्य समीकरण को तापीय चालन # फूरियर के नियम | फूरियर के नियम (ताप अभिवाह तापमान प्रवणता के समानुपाती होता है) के साथ जोड़ा जा सकता है। ऊष्मा अभिवाह के समीकरण में स्रोत की शर्तें भी हो सकती हैं: हालांकि ऊर्जा को बनाया या नष्ट नहीं किया जा सकता है, गर्मी को अन्य प्रकार की ऊर्जा से बनाया जा सकता है, उदाहरण के लिए घर्षण या [[जूल हीटिंग]] के माध्यम से। | ||
== संभाव्यता वितरण == | == संभाव्यता वितरण == | ||
यदि कोई ऐसी | यदि कोई ऐसी राशि है जो स्टोचैस्टिक (यादृच्छिक) प्रक्रिया के अनुसार लगातार चलती है, जैसे कि [[एक प्रकार कि गति]] के साथ एकल विघटित अणु का स्थान, तो इसके संभाव्यता वितरण के लिए एक सांतत्य समीकरण है। इस मामले में अभिवाह प्रति इकाई क्षेत्र प्रति इकाई समय की संभावना है कि कण एक सतह से गुजरता है। सांतत्य समीकरण के अनुसार, इस अभिवाह का नकारात्मक विचलन संभाव्यता घनत्व के परिवर्तन की दर के बराबर है। सांतत्य समीकरण इस तथ्य को दर्शाता है कि अणु सदैव कहीं होता है - इसकी संभावना वितरण का समाकल अंग सदैव 1 के बराबर होता है - और यह एक निरंतर गति (कोई स्थानांतरणेशन) से चलता है। | ||
== क्वांटम यांत्रिकी == | == क्वांटम यांत्रिकी == | ||
<!-- This section is linked from [[Conservation law (physics)|Conservation law]] --> | <!-- This section is linked from [[Conservation law (physics)|Conservation law]] --> | ||
[[क्वांटम यांत्रिकी]] एक अन्य डोमेन है जहां संभाव्यता के संरक्षण से संबंधित एक | [[क्वांटम यांत्रिकी]] एक अन्य डोमेन है जहां संभाव्यता के संरक्षण से संबंधित एक सांतत्य समीकरण है। समीकरण में शर्तों के लिए निम्नलिखित परिभाषाओं की आवश्यकता होती है, और उपरोक्त अन्य उदाहरणों की तुलना में थोड़ा कम स्पष्ट है, इसलिए उन्हें यहां रेखांकित किया गया है: | ||
* तरंग समारोह {{math|Ψ}} स्थिति और संवेग स्थान (बजाय स्थिति और संवेग स्थान) में एक [[कण]] के लिए, | * तरंग समारोह {{math|Ψ}} स्थिति और संवेग स्थान (बजाय स्थिति और संवेग स्थान) में एक [[कण]] के लिए, अर्थात स्थिति का एक कार्य {{math|'''r'''}} और समय {{math|''t''}}, {{math|1=Ψ = Ψ('''r''', ''t'')}}. | ||
* प्रायिकता घनत्व फलन है <math display="block">\rho(\mathbf{r}, t) = \Psi^{*}(\mathbf{r}, t)\Psi(\mathbf{r}, t) = |\Psi(\mathbf{r}, t)|^2. </math> | * प्रायिकता घनत्व फलन है <math display="block">\rho(\mathbf{r}, t) = \Psi^{*}(\mathbf{r}, t)\Psi(\mathbf{r}, t) = |\Psi(\mathbf{r}, t)|^2. </math> | ||
* कण के भीतर खोजने की [[संभावना]] {{mvar|V}} पर {{mvar|t}} द्वारा दर्शाया और परिभाषित किया गया है <math display="block">P = P_{\mathbf{r} \in V}(t) = \int_V \Psi^*\Psi dV = \int_V |\Psi|^2 dV.</math> | * कण के भीतर खोजने की [[संभावना]] {{mvar|V}} पर {{mvar|t}} द्वारा दर्शाया और परिभाषित किया गया है <math display="block">P = P_{\mathbf{r} \in V}(t) = \int_V \Psi^*\Psi dV = \int_V |\Psi|^2 dV.</math> | ||
* [[संभाव्यता वर्तमान]] (उर्फ संभाव्यता प्रवाह) है <math display="block">\mathbf{j}(\mathbf{r}, t) = \frac{\hbar}{2mi} \left[ \Psi^{*} \left( \nabla\Psi \right) - \Psi \left( \nabla\Psi^{*} \right) \right].</math> | * [[संभाव्यता वर्तमान]] (उर्फ संभाव्यता प्रवाह) है <math display="block">\mathbf{j}(\mathbf{r}, t) = \frac{\hbar}{2mi} \left[ \Psi^{*} \left( \nabla\Psi \right) - \Psi \left( \nabla\Psi^{*} \right) \right].</math> | ||
इन परिभाषाओं के साथ | इन परिभाषाओं के साथ सांतत्य समीकरण पढ़ता है: | ||
<math display="block">\nabla \cdot \mathbf{j} + \frac{\partial\rho}{\partial t} = 0 \mathrel{\rightleftharpoons} \nabla \cdot \mathbf{j} + \frac{\partial |\Psi|^2}{\partial t} = 0.</math> | <math display="block">\nabla \cdot \mathbf{j} + \frac{\partial\rho}{\partial t} = 0 \mathrel{\rightleftharpoons} \nabla \cdot \mathbf{j} + \frac{\partial |\Psi|^2}{\partial t} = 0.</math> | ||
कोई भी प्रपत्र उद्धृत किया जा सकता है। सहज रूप से, उपरोक्त | कोई भी प्रपत्र उद्धृत किया जा सकता है। सहज रूप से, उपरोक्त राशि इंगित करती हैं कि यह संभाव्यता के अभिवाह का प्रतिनिधित्व करता है। कण को किसी स्थान पर खोजने की संभावना {{math|'''r'''}} और समय {{mvar|t}} द्रव की तरह प्रवाहित होता है; इसलिए पद प्रायिकता धारा, एक सदिश क्षेत्र। कण ही इस सदिश क्षेत्र में [[नियतात्मक प्रणाली]] को प्रवाहित नहीं करता है। | ||
{{math proof|title=Consistency with Schrödinger equation|proof= | {{math proof|title=Consistency with Schrödinger equation|proof= | ||
| Line 221: | Line 223: | ||
== सेमीकंडक्टर == | == सेमीकंडक्टर == | ||
सेमीकंडक्टर में कुल करंट | सेमीकंडक्टर में कुल करंट अभिवाह में प्रवाहकत्त्व बैंड और वैलेंस बैंड में छेद दोनों इलेक्ट्रॉनों के प्रवाहित होाव अभिवाह और प्रसार अभिवाह होते हैं। | ||
एक आयाम में इलेक्ट्रॉनों के लिए सामान्य रूप: | एक आयाम में इलेक्ट्रॉनों के लिए सामान्य रूप: | ||
| Line 247: | Line 249: | ||
यह खंड इलेक्ट्रॉनों के लिए उपरोक्त समीकरण की व्युत्पत्ति प्रस्तुत करता है। छिद्रों के समीकरण के लिए एक समान व्युत्पत्ति पाई जा सकती है। | यह खंड इलेक्ट्रॉनों के लिए उपरोक्त समीकरण की व्युत्पत्ति प्रस्तुत करता है। छिद्रों के समीकरण के लिए एक समान व्युत्पत्ति पाई जा सकती है। | ||
इस तथ्य पर विचार करें कि एक्स-अक्ष के साथ क्रॉस-अनुभागीय क्षेत्र, ए, और लंबाई, डीएक्स के साथ अर्धचालक सामग्री की | इस तथ्य पर विचार करें कि एक्स-अक्ष के साथ क्रॉस-अनुभागीय क्षेत्र, ए, और लंबाई, डीएक्स के साथ अर्धचालक सामग्री की राशि में इलेक्ट्रॉनों की संख्या संरक्षित है। अधिक सटीक, कोई कह सकता है: | ||
<math display="block">\text{Rate of change of electron density} = (\text{Electron flux in} - \text{Electron flux out}) + \text{Net generation inside a volume}</math> | <math display="block">\text{Rate of change of electron density} = (\text{Electron flux in} - \text{Electron flux out}) + \text{Net generation inside a volume}</math> | ||
गणितीय रूप से, इस समानता को लिखा जा सकता है: | गणितीय रूप से, इस समानता को लिखा जा सकता है: | ||
| Line 254: | Line 256: | ||
\frac{dn}{dt} A \, dx &= [J(x)+\frac{dJ}{dx}dx-J(x)]\frac{A}{e} + (G_n - R_n)A \, dx \\[3pt] | \frac{dn}{dt} A \, dx &= [J(x)+\frac{dJ}{dx}dx-J(x)]\frac{A}{e} + (G_n - R_n)A \, dx \\[3pt] | ||
\frac{dn}{dt} &= \frac{1}{e}\frac{dJ}{dx} + (G_n - R_n) | \frac{dn}{dt} &= \frac{1}{e}\frac{dJ}{dx} + (G_n - R_n) | ||
\end{align}</math>यहाँ J सेमीकंडक्टर के विचारित आयतन के भीतर इलेक्ट्रॉन | \end{align}</math>यहाँ J सेमीकंडक्टर के विचारित आयतन के भीतर इलेक्ट्रॉन अभिवाह के कारण वर्तमान घनत्व (जिसकी दिशा परिपाटी द्वारा इलेक्ट्रॉन अभिवाह के विरुद्ध है) को दर्शाता है। इसे इलेक्ट्रॉन धारा घनत्व भी कहते हैं। | ||
कुल इलेक्ट्रॉन वर्तमान घनत्व | कुल इलेक्ट्रॉन वर्तमान घनत्व प्रवाहित होाव वर्तमान और प्रसार वर्तमान घनत्व का योग है: | ||
<math display="block">J_n = en\mu_nE + eD_n\frac{dn}{dx}</math> | <math display="block">J_n = en\mu_nE + eD_n\frac{dn}{dx}</math> | ||
इसलिए, हमारे पास है | इसलिए, हमारे पास है | ||
<math display="block">\frac{dn}{dt} = \frac{1}{e}\frac{d}{dx}\left(en\mu_n E + eD_n\frac{dn}{dx}\right) + (G_n - R_n)</math> | <math display="block">\frac{dn}{dt} = \frac{1}{e}\frac{d}{dx}\left(en\mu_n E + eD_n\frac{dn}{dx}\right) + (G_n - R_n)</math> | ||
उत्पाद नियम को | उत्पाद नियम को प्रयुक्त करने से अंतिम अभिव्यक्ति होती है: | ||
<math display="block">\frac{dn}{dt} = \mu_n E\frac{dn}{dx} + \mu_n n\frac{dE}{dx} + D_n\frac{d^2 n}{dx^2} + (G_n - R_n)</math> | <math display="block">\frac{dn}{dt} = \mu_n E\frac{dn}{dx} + \mu_n n\frac{dE}{dx} + D_n\frac{d^2 n}{dx^2} + (G_n - R_n)</math> | ||
=== समाधान === | === समाधान === | ||
इन समीकरणों को वास्तविक उपकरणों में हल करने की कुंजी जब भी संभव हो ऐसे क्षेत्रों का चयन करना है जिनमें अधिकांश तंत्र नगण्य हैं ताकि समीकरण | इन समीकरणों को वास्तविक उपकरणों में हल करने की कुंजी जब भी संभव हो ऐसे क्षेत्रों का चयन करना है जिनमें अधिकांश तंत्र नगण्य हैं ताकि समीकरण प्रवाहित होुत सरल रूप में कम हो जाएं। | ||
== सापेक्षतावादी संस्करण == | == सापेक्षतावादी संस्करण == | ||
| Line 272: | Line 274: | ||
{{see also|4-vector}} | {{see also|4-vector}} | ||
[[विशेष सापेक्षता]] के अंकन और उपकरण, विशेष रूप से [[4-वेक्टर]] और [[4-ढाल]], किसी भी | [[विशेष सापेक्षता]] के अंकन और उपकरण, विशेष रूप से [[4-वेक्टर|4-सदिश]] और [[4-ढाल]], किसी भी सांतत्य समीकरण को लिखने का एक सुविधाजनक तरीका प्रदान करते हैं। | ||
किसी | किसी राशि का घनत्व {{math|''ρ''}} और इसका करंट {{math|'''j'''}} को 4-सदिश में जोड़ा जा सकता है जिसे [[4-वर्तमान]] कहा जाता है: | ||
<math display="block">J = \left(c \rho, j_x, j_y, j_z \right)</math> | <math display="block">J = \left(c \rho, j_x, j_y, j_z \right)</math> | ||
कहाँ {{math|''c''}} [[प्रकाश की गति]] है। इस धारा का 4-विचलन है: | कहाँ {{math|''c''}} [[प्रकाश की गति]] है। इस धारा का 4-विचलन है: | ||
<math display="block"> \partial_\mu J^\mu = c \frac{ \partial \rho}{\partial ct} + \nabla \cdot \mathbf{j}</math> | <math display="block"> \partial_\mu J^\mu = c \frac{ \partial \rho}{\partial ct} + \nabla \cdot \mathbf{j}</math> | ||
कहाँ {{math|∂<sub>''μ''</sub>}} 4-ढाल है और {{math|''μ''}} [[ अंतरिक्ष समय ]] [[आयाम]] को लेबल करने वाला एक [[ सूचकांक अंकन ]] है। फिर | कहाँ {{math|∂<sub>''μ''</sub>}} 4-ढाल है और {{math|''μ''}} [[ अंतरिक्ष समय | स्थान समय]] [[आयाम]] को लेबल करने वाला एक [[ सूचकांक अंकन ]] है। फिर सांतत्य समीकरण है: | ||
<math display="block">\partial_\mu J^\mu = 0</math> | <math display="block">\partial_\mu J^\mu = 0</math> | ||
सामान्य मामले में जहां कोई स्रोत या | सामान्य मामले में जहां कोई स्रोत या मंद नहीं हैं, अर्थात ऊर्जा या चार्ज जैसी पूरी तरह से संरक्षित राशि के लिए। यह सांतत्य समीकरण प्रकट रूप से (स्पष्ट रूप से) [[लोरेंत्ज़ अपरिवर्तनीय]] है। | ||
इस रूप में | इस रूप में प्रायः लिखे जाने वाले सांतत्य समीकरणों के उदाहरणों में विद्युत आवेश संरक्षण सम्मिलित है | ||
<math display="block">\partial_\mu J^\mu = 0</math> | <math display="block">\partial_\mu J^\mu = 0</math> | ||
कहाँ {{math|''J''}} विद्युत 4-धारा है; और ऊर्जा-संवेग संरक्षण | कहाँ {{math|''J''}} विद्युत 4-धारा है; और ऊर्जा-संवेग संरक्षण | ||
| Line 289: | Line 291: | ||
=== [[सामान्य सापेक्षता]] === | === [[सामान्य सापेक्षता]] === | ||
सामान्य सापेक्षता में, जहां | सामान्य सापेक्षता में, जहां स्थान-समय घुमावदार होता है, ऊर्जा, आवेश या अन्य संरक्षित राशियों के लिए सांतत्य समीकरण (अंतर रूप में) में साधारण विचलन के बजाय सहसंयोजक व्युत्पन्न सम्मिलित होता है। | ||
उदाहरण के लिए, तनाव-ऊर्जा टेंसर एक दूसरे क्रम का [[टेंसर क्षेत्र]] है जिसमें द्रव्यमान-ऊर्जा वितरण के ऊर्जा-संवेग घनत्व, ऊर्जा-संवेग | उदाहरण के लिए, तनाव-ऊर्जा टेंसर एक दूसरे क्रम का [[टेंसर क्षेत्र]] है जिसमें द्रव्यमान-ऊर्जा वितरण के ऊर्जा-संवेग घनत्व, ऊर्जा-संवेग अभिवाह और कतरनी तनाव होते हैं। सामान्य सापेक्षता में ऊर्जा-संवेग संरक्षण का अंतर रूप बताता है कि तनाव-ऊर्जा टेंसर का सहसंयोजक विचलन शून्य है: | ||
<math display="block">{T^\mu}_{\nu; \mu} = 0.</math> | <math display="block">{T^\mu}_{\nu; \mu} = 0.</math> | ||
सामान्य सापेक्षता में आइंस्टीन क्षेत्र समीकरणों के रूप में यह एक महत्वपूर्ण बाधा है।<ref>{{cite book |title=रिलेटिविटी डीमिस्टीफाइड|author=D. McMahon|publisher=McGraw Hill (USA)|year=2006|isbn=0-07-145545-0}}</ref> | सामान्य सापेक्षता में आइंस्टीन क्षेत्र समीकरणों के रूप में यह एक महत्वपूर्ण बाधा है।<ref>{{cite book |title=रिलेटिविटी डीमिस्टीफाइड|author=D. McMahon|publisher=McGraw Hill (USA)|year=2006|isbn=0-07-145545-0}}</ref> | ||
हालांकि, वक्रीय निर्देशांक में साधारण टेन्सर # तनाव-ऊर्जा टेंसर के दूसरे क्रम के टेन्सर क्षेत्र आवश्यक रूप से | हालांकि, वक्रीय निर्देशांक में साधारण टेन्सर # तनाव-ऊर्जा टेंसर के दूसरे क्रम के टेन्सर क्षेत्र आवश्यक रूप से नष्ट नहीं होते हैं:<ref>{{cite book |title=आकर्षण-शक्ति|author=C.W. Misner |last2=K.S. Thorne |last3=J.A. Wheeler | publisher=W.H. Freeman & Co |year=1973 |isbn=0-7167-0344-0}}</ref> | ||
<math display="block">\partial_{\mu} T^{\mu\nu} = - \Gamma^{\mu}_{\mu \lambda} T^{\lambda \nu} - \Gamma^{\nu}_{\mu \lambda} T^{\mu \lambda},</math> | <math display="block">\partial_{\mu} T^{\mu\nu} = - \Gamma^{\mu}_{\mu \lambda} T^{\lambda \nu} - \Gamma^{\nu}_{\mu \lambda} T^{\mu \lambda},</math> | ||
केवल समतल ज्यामिति के लिए दाहिना भाग पूरी तरह से | केवल समतल ज्यामिति के लिए दाहिना भाग पूरी तरह से नष्ट हो जाता है। | ||
परिणामस्वरूप, | परिणामस्वरूप, सांतत्य समीकरण के समाकल रूप को परिभाषित करना मुश्किल है और जरूरी नहीं कि उस क्षेत्र के लिए मान्य हो, जिसके भीतर स्पेसटाइम महत्वपूर्ण रूप से वक्रित हो (उदाहरण के लिए एक ब्लैक होल के आसपास, या पूरे ब्रह्मांड में)।<ref>{{cite web |url=http://math.ucr.edu/home/baez/physics/Relativity/GR/energy_gr.html |title=Is Energy Conserved in General Relativity? |access-date=2014-04-25 |author1=Michael Weiss |author2=John Baez }}</ref> | ||
== कण भौतिकी == | == कण भौतिकी == | ||
[[क्वार्क]] और ग्लून्स का रंग आवेश होता है, जो | [[क्वार्क]] और ग्लून्स का रंग आवेश होता है, जो सदैव विद्युत आवेश की तरह संरक्षित होता है, और ऐसे रंग आवेश धाराओं के लिए एक सांतत्य समीकरण होता है (धाराओं के लिए स्पष्ट अभिव्यक्तियाँ ग्लूऑन क्षेत्र शक्ति टेंसर # गति के समीकरण में दी गई हैं)। | ||
कण भौतिकी में कई अन्य | कण भौतिकी में कई अन्य राशि हैं जो प्रायः या सदैव संरक्षित होती हैं: बेरिऑन संख्या (क्वार्क की संख्या के अनुपात में प्रतिक्वार्क की संख्या को घटाकर), लेप्टान संख्या|इलेक्ट्रॉन संख्या, एमयू संख्या, ताऊ संख्या, [[ समभारिक प्रचक्रण ]], और अन्य।<ref>{{Cite book|title=आकर्षण-शक्ति|author1=J.A. Wheeler |author2=C. Misner |author3=K.S. Thorne |publisher=W.H. Freeman & Co | year=1973| pages=558–559 | isbn=0-7167-0344-0}}</ref> इनमें से प्रत्येक का संगत सांतत्य समीकरण है, संभवतः स्रोत/मंद शर्तों सहित। | ||
== नोएदर का प्रमेय == | == नोएदर का प्रमेय == | ||
| Line 311: | Line 313: | ||
{{for|more detailed explanations and derivations|Noether's theorem}} | {{for|more detailed explanations and derivations|Noether's theorem}} | ||
भौतिकी में | भौतिकी में प्रायः संरक्षण समीकरणों के होने का एक कारण नोएदर का प्रमेय है। यह बताता है कि जब भी भौतिकी के नियमों में [[निरंतर समरूपता]] होती है, तो कुछ संरक्षित भौतिक राशि के लिए एक सांतत्य समीकरण होता है। तीन सबसे प्रचलित उदाहरण हैं: | ||
* [[ समय अनुवाद ]] के संबंध में भौतिकी के नियम अपरिवर्तनीय हैं | टाइम-ट्रांसलेशन- उदाहरण के लिए, भौतिकी के नियम आज भी वैसे ही हैं जैसे कल थे। यह समरूपता ऊर्जा के संरक्षण के लिए | * [[ समय अनुवाद ]] के संबंध में भौतिकी के नियम अपरिवर्तनीय हैं | टाइम-ट्रांसलेशन- उदाहरण के लिए, भौतिकी के नियम आज भी वैसे ही हैं जैसे कल थे। यह समरूपता ऊर्जा के संरक्षण के लिए सांतत्य समीकरण की ओर ले जाती है। | ||
* भौतिकी के नियम | * भौतिकी के नियम स्थान-अनुवाद के संबंध में अपरिवर्तनीय हैं- उदाहरण के लिए, ब्राजील में भौतिकी के नियम अर्जेंटीना में भौतिकी के नियमों के समान हैं। यह समरूपता गति के संरक्षण के लिए सांतत्य समीकरण की ओर ले जाती है। | ||
* अभिविन्यास के संबंध में भौतिकी के नियम अपरिवर्तनीय हैं—उदाहरण के लिए, बाह्य | * अभिविन्यास के संबंध में भौतिकी के नियम अपरिवर्तनीय हैं—उदाहरण के लिए, बाह्य स्थान में तैरते हुए, ऐसा कोई माप नहीं है जिससे आप यह कह सकें कि कौन सा मार्ग ऊपर की ओर है; आप कैसे उन्मुख हैं, भौतिकी के नियम समान हैं। यह समरूपता कोणीय गति के संरक्षण के लिए सांतत्य समीकरण की ओर ले जाती है। | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[वन-वे वेव समीकरण]] | * [[वन-वे वेव समीकरण]] | ||
* संरक्षण | * संरक्षण नियम (भौतिकी) | ||
* [[संरक्षण प्रपत्र]] | * [[संरक्षण प्रपत्र]] | ||
* अपव्यय प्रणाली | * अपव्यय प्रणाली | ||
Revision as of 13:27, 27 June 2023
| Part of a series on |
| सातत्यक यांत्रिकी |
|---|
सांतत्य समीकरण या अभिगमन समीकरण एक समीकरण है जो कुछ राशि के अभिगमन का वर्णन करता है। संरक्षित राशि पर प्रयुक्त होने पर यह विशेष रूप से सरल और प्रभावशाली होता है, लेकिन इसे किसी भी व्यापक राशि पर प्रयुक्त करने के लिए सामान्यीकृत किया जा सकता है। चूँकि द्रव्यमान, ऊर्जा, संवेग, विद्युत आवेश और अन्य प्राकृतिक राशि उनकी संबंधित उपयुक्त परिस्थितियों में संरक्षित होती हैं, इसलिए सांतत्य समीकरणों का उपयोग करके विभिन्न प्रकार की भौतिक घटनाओं का वर्णन किया जा सकता है।
सांतत्य समीकरण संरक्षण नियम (भौतिकी) का एक प्रबल, स्थानीय रूप है। उदाहरण के लिए, ऊर्जा संरक्षण के नियम का एक दुर्बल संस्करण बताता है कि ऊर्जा को न तो बनाया जा सकता है और न ही नष्ट किया जा सकता है - अर्थात, ब्रह्मांड में ऊर्जा की कुल राशि निश्चित है। यह कथन इस संभावना से अस्वीकृत नहीं करता है कि ऊर्जा की एक राशि एक बिंदु से नष्ट हो सकती है जबकि एक साथ दूसरे बिंदु पर दिखाई दे सकती है। एक प्रबल कथन यह है कि ऊर्जा स्थानीय रूप से संरक्षित होती है: ऊर्जा को न तो बनाया जा सकता है और न ही नष्ट किया जा सकता है, न ही इसे एक स्थान से दूसरे स्थान पर "स्थानांतरण" किया जा सकता है - यह केवल निरंतर अभिवाह (फ्लक्स) द्वारा स्थानांतरित हो सकती है। सांतत्य समीकरण इस प्रकार के कथन को व्यक्त करने का गणितीय तरीका है। उदाहरण के लिए, विद्युत आवेश के लिए सांतत्य समीकरण बताता है कि स्थान के किसी भी आयतन में विद्युत आवेश की मात्रा केवल उस आयतन की सीमाओं के माध्यम से उसके अंदर या बाहर प्रवाहित होने वाली विद्युत धारा की राशि से बदल सकती है।
सांतत्य समीकरणों में सामान्य रूप से स्रोत और मंद शब्द सम्मिलित हो सकते हैं, जो उन्हें उन राशियों का वर्णन करने की अनुमति देते हैं जो प्रायः होती हैं लेकिन सदैव संरक्षित नहीं होती हैं, जैसे आणविक प्रजातियों का घनत्व जो रासायनिक प्रतिक्रियाओं द्वारा बनाया या नष्ट किया जा सकता है। दैनिक जीवन के उदाहरण में, जीवित लोगों की संख्या के लिए एक सांतत्य समीकरण है; इसमें जन्म लेने वाले लोगों के लिए एक स्रोत शब्द है, और मरने वाले लोगों के लिए एक मंद शब्द है।
किकिसी भी सांतत्य समीकरण को "समाकल रूप" (अभिवाह समाकल के संदर्भ में) में व्यक्त किया जा सकता है, जो किसी भी परिमित क्षेत्र पर प्रयुक्त होता है, या "अवकल रूप" (विचलन संचालिका के संदर्भ में) में व्यक्त किया जा सकता है जो एक बिंदु पर प्रयुक्त होता है।
सांतत्य समीकरण अधिक विशिष्ट अभिगमन समीकरणों जैसे कि संवहन-प्रसार समीकरण, बोल्ट्ज़मैन अभिगमन समीकरण और नेवियर-स्टोक्स समीकरणों के अंतर्गत आते हैं।
सांतत्य समीकरणों द्वारा नियंत्रित अभिवाह को सैंकी आरेख का उपयोग करके देखा जा सकता है।
सामान्य समीकरण
अभिवाह की परिभाषा
जब अभिवाह को परिभाषित किया जा सकता है तो सांतत्य समीकरण उपयोगी होता है। अभिवाह को परिभाषित करने के लिए सबसे पहले एक मात्रा q होनी चाहिए जो प्रवाहित या गति कर सके, जैसे द्रव्यमान, ऊर्जा, विद्युत आवेश, संवेग, अणुओं की संख्या, आदि सम्मिलित है। मान लीजिए ρ इस राशि का आयतन घनत्व है जो प्रति इकाई आयतन q की मात्रा है।
जिस तरह से यह मात्रा q प्रवाहित हो रही है उसका वर्णन इसके अभिवाह द्वारा किया जाता है। q का अभिवाह एक सदिश क्षेत्र है, जिसे हम j के रूप में दर्शाते हैं। यहां अभिवाह के कुछ उदाहरण और गुण दिए गए हैं:
- अभिवाह का आयाम "एक इकाई क्षेत्र के माध्यम से प्रति इकाई समय में प्रवाहित q की मात्रा" है। उदाहरण के लिए, प्रवाहित पानी के लिए द्रव्यमान सांतत्य समीकरण में, यदि 1 cm2 प्रतिनिध्यात्मक क्षेत्र वाले पाइप के माध्यम से 1 ग्राम प्रति सेकंड पानी प्रवाहित हो रहा है, तो पाइप के अंदर औसत द्रव्यमान अभिवाह j (1 g/s)/cm2 है। और इसकी दिशा पाइप के साथ उस दिशा में होती है जिस दिशा में पानी प्रवाहित हो रहा है। पाइप के बाहर, जहां पानी नहीं है, अभिवाह शून्य है।
- यदि कोई वेग क्षेत्र u है जो प्रासंगिक अभिवाह का वर्णन करता है - दूसरे शब्दों में, यदि बिंदु x पर सभी मात्रा q वेग u(x) के साथ घूम रही है - तो परिभाषा के अनुसार अभिवाह वेग क्षेत्र के घनत्व गुना के बराबर है :
- उदाहरण के लिए, यदि प्रवाहित पानी के द्रव्यमान सांतत्य समीकरण में, u प्रत्येक बिंदु पर पानी का वेग है, और ρ प्रत्येक बिंदु पर पानी का घनत्व है, तब j द्रव्यमान अभिवाह होगा।
- एक प्रचलित उदाहरण में, विद्युत आवेश का अभिवाह विद्युत अभिवाह घनत्व है।
- यदि कोई काल्पनिक सतह S है, तो S पर अभिवाह का सतह समाकल q की मात्रा के बराबर है जो प्रति इकाई समय में सतह S से गुजर रहा है:
- जिसमें एक सतह समाकल है।
ध्यान दें कि जिस अवधारणा को यहां ''अभिवाह'' कहा गया है, उसे कुछ साहित्य में वैकल्पिक रूप से "अभिवाह घनत्व" कहा जाता है, जिसके संदर्भ में ''अभिवाह'' या अभिवाह घनत्व के सतह समाकल को दर्शाता है। विवरण के लिए अभिवाह पर मुख्य लेख देखें।
समाकल रूप
सांतत्य समीकरण का समाकल रूप बताता है कि:
- किसी क्षेत्र में q की मात्रा तब बढ़ती है जब अतिरिक्त q क्षेत्र की सतह से अंदर की ओर प्रवाहित है, और जब यह बाहर की ओर प्रवाहित है तो घट जाती है;
- किसी क्षेत्र में q की मात्रा तब बढ़ती है जब क्षेत्र के अंदर नया q बनाया जाता है, और q नष्ट होने पर घट जाती है;
- इन दो प्रक्रियाओं के अतिरिक्त, किसी क्षेत्र में q की मात्रा को बदलने का कोई अन्य तरीका नहीं है।
गणितीय रूप से, आयतन V के अंदर q की वृद्धि की दर को व्यक्त करने वाले सांतत्य समीकरण का समाकल रूप है:
![]()

जहां
- S कोई काल्पनिक संवृत सतह है, जो आयतन V को घेरती है,
-
 S dS उस संवृत सतह पर सतह समाकल को दर्शाता है,
S dS उस संवृत सतह पर सतह समाकल को दर्शाता है, - q आयतन V में मात्रा की कुल राशि है,
- j, q का प्रवाह है
- t समय है, edit
- Σ शुद्ध दर है कि q वॉल्यूम के अंदर उत्पन्न हो रहा है V प्रति यूनिट समय। कब q उत्पन्न हो रहा है, इसे का स्रोत कहते हैं q, और यह बनाता है Σ अधिक सकारात्मक। कब q नष्ट हो रहा है, इसे मंद कहा जाता है q, और यह बनाता है Σ अधिक नकारात्मक। यह शब्द कभी-कभी लिखा जाता है या नियंत्रण आयतन के अंदर इसकी उत्पत्ति या विनाश से क्यू का कुल परिवर्तन।
एक साधारण उदाहरण में, V एक इमारत हो सकती है, और q इमारत में लोगों की संख्या हो सकती है। सतह S में भवन की दीवारें, दरवाजे, छत और नींव सम्मिलित होगी। फिर सांतत्य समीकरण बताता है कि जब लोग इमारत में प्रवेश करते हैं तो लोगों की संख्या बढ़ जाती है (सतह के माध्यम से एक आवक प्रवाह), जब लोग इमारत से बाहर निकलते हैं (सतह के माध्यम से एक बाहरी प्रवाह), घट जाती है जब इमारत में कोई व्यक्ति देता है जन्म (एक स्रोत, Σ > 0), और घटता है जब इमारत में किसी की मृत्यु हो जाती है (एक मंद, Σ < 0).
अवकल रूप
विचलन प्रमेय द्वारा, एक सामान्य सांतत्य समीकरण को अंतर रूप में भी लिखा जा सकता है:
कहाँ
- ∇⋅ विचलन है,
- ρ राशि की राशि है q प्रति इकाई आयतन,
- j का अभिवाह घनत्व है q,
- t यह समय है,
- σ की पीढ़ी है q प्रति इकाई आयतन प्रति इकाई समय। उत्पन्न करने वाली शर्तें q (अर्थात।, σ > 0) या हटा दें q (अर्थात।, σ < 0) को क्रमशः स्रोत और मंद कहा जाता है।
इस सामान्य समीकरण का उपयोग किसी भी सांतत्य समीकरण को प्राप्त करने के लिए किया जा सकता है, जो वॉल्यूम सांतत्य समीकरण के रूप में सरल से लेकर नेवियर-स्टोक्स समीकरण के रूप में जटिल है। यह समीकरण संवहन समीकरण का भी सामान्यीकरण करता है। भौतिकी में अन्य समीकरण, जैसे कि गॉस का नियम | विद्युत क्षेत्र का गॉस का नियम और गुरुत्वाकर्षण के लिए गॉस का नियम, सांतत्य समीकरण के समान गणितीय रूप है, लेकिन सामान्य रूप से शब्द सांतत्य समीकरण द्वारा संदर्भित नहीं किया जाता है, क्योंकि j उन मामलों में वास्तविक भौतिक राशि के अभिवाह का प्रतिनिधित्व नहीं करता है।
उस मामले में q एक संरक्षण नियम (भौतिकी) है जिसे बनाया या नष्ट नहीं किया जा सकता (जैसे ऊर्जा), σ = 0 और समीकरण बन जाते हैं:
विद्युत चुंबकत्व
विद्युत चुम्बकीय सिद्धांत में, सांतत्य समीकरण एक अनुभवजन्य नियम है जो चार्ज संरक्षण (स्थानीय) व्यक्त करता है। गणितीय रूप से यह मैक्सवेल के समीकरणों का स्वत: परिणाम है, हालांकि चार्ज संरक्षण मैक्सवेल के समीकरणों की तुलना में अधिक मौलिक है। यह बताता है कि वर्तमान घनत्व का विचलन J (एम्पीयर प्रति वर्ग मीटर में) आवेश घनत्व के परिवर्तन की ऋणात्मक दर के बराबर है ρ (कूलम्ब प्रति घन मीटर में),
One of Maxwell's equations, Ampère's law (with Maxwell's correction), states that
Taking the divergence of both sides (the divergence and partial derivative in time commute) results in
But Gauss's law (another Maxwell equation), states that
करंट आवेश की गति है। सांतत्य समीकरण कहता है कि यदि आवेश एक अवकल आयतन से बाहर निकल रहा है (अर्थात, वर्तमान घनत्व का विचलन धनात्मक है) तो उस आयतन के भीतर आवेश की मात्रा घटने वाली है, इसलिए आवेश घनत्व के परिवर्तन की दर ऋणात्मक है। इसलिए, सांतत्य समीकरण आवेश के संरक्षण के बराबर है।
यदि चुंबकीय मोनोपोल मौजूद हैं, तो मोनोपोल धाराओं के लिए सांतत्य समीकरण भी होगा, पृष्ठभूमि के लिए मोनोपोल आलेख और विद्युत और चुंबकीय धाराओं के बीच द्वंद्व देखें।
द्रव गतिकी
द्रव गतिकी में, सांतत्य समीकरण बताता है कि जिस दर पर द्रव्यमान एक प्रणाली में प्रवेश करता है वह उस दर के बराबर होता है जिस पर द्रव्यमान प्रणाली को छोड़ देता है और साथ ही प्रणाली के भीतर द्रव्यमान का संचय होता है।[1][2] सांतत्य समीकरण का अंतर रूप है:[1]
- ρ द्रव घनत्व है,
- t यह समय है,
- u अभिवाह वेग सदिश क्षेत्र है।
समय व्युत्पन्न को प्रणाली में द्रव्यमान के संचय (या हानि) के रूप में समझा जा सकता है, जबकि विचलन शब्द अभिवाह बनाम अभिवाह में अंतर का प्रतिनिधित्व करता है। इस संदर्भ में, यह समीकरण भी यूलर समीकरणों (द्रव गतिकी) में से एक है। नेवियर-स्टोक्स समीकरण रैखिक गति के संरक्षण का वर्णन करते हुए एक सदिश सांतत्य समीकरण बनाते हैं।
यदि तरल असंपीड्य अभिवाह है (वॉल्यूमेट्रिक तनाव दर शून्य है), द्रव्यमान सांतत्य समीकरण वॉल्यूम सांतत्य समीकरण को सरल बनाता है:[3]
कंप्यूटर दृष्टि
कंप्यूटर दृष्टि में, ऑप्टिकल अभिवाह दृश्य दृश्य में वस्तुओं की स्पष्ट गति का पैटर्न है। इस धारणा के तहत कि गतिमान वस्तु की चमक दो छवि फ़्रेमों के बीच नहीं बदली, कोई ऑप्टिकल अभिवाह समीकरण को इस प्रकार प्राप्त कर सकता है:
- t यह समय है,
- x, y छवि में निर्देशांक करता है,
- I छवि निर्देशांक पर छवि तीव्रता है (x, y) और समय t,
- V ऑप्टिकल अभिवाह वेग सदिश है छवि समन्वय पर (x, y) और समय t
ऊर्जा और ताप
ऊर्जा का संरक्षण कहता है कि ऊर्जा को न तो बनाया जा सकता है और न ही नष्ट किया जा सकता है। (सामान्य सापेक्षता से जुड़ी बारीकियों के लिए #सामान्य सापेक्षता देखें।) इसलिए, ऊर्जा अभिवाह के लिए एक सांतत्य समीकरण है:
- u, स्थानीय ऊर्जा घनत्व (ऊर्जा प्रति इकाई आयतन),
- q, एक सदिश के रूप में ऊर्जा अभिवाह (प्रति यूनिट क्रॉस-अनुभागीय क्षेत्र प्रति यूनिट समय में ऊर्जा का हस्तांतरण),
एक महत्वपूर्ण व्यावहारिक उदाहरण गर्मी का हस्तांतरण है। जब गर्मी एक ठोस के अंदर प्रवाहित होती है, तो ऊष्मा समीकरण पर पहुंचने के लिए सांतत्य समीकरण को तापीय चालन # फूरियर के नियम | फूरियर के नियम (ताप अभिवाह तापमान प्रवणता के समानुपाती होता है) के साथ जोड़ा जा सकता है। ऊष्मा अभिवाह के समीकरण में स्रोत की शर्तें भी हो सकती हैं: हालांकि ऊर्जा को बनाया या नष्ट नहीं किया जा सकता है, गर्मी को अन्य प्रकार की ऊर्जा से बनाया जा सकता है, उदाहरण के लिए घर्षण या जूल हीटिंग के माध्यम से।
संभाव्यता वितरण
यदि कोई ऐसी राशि है जो स्टोचैस्टिक (यादृच्छिक) प्रक्रिया के अनुसार लगातार चलती है, जैसे कि एक प्रकार कि गति के साथ एकल विघटित अणु का स्थान, तो इसके संभाव्यता वितरण के लिए एक सांतत्य समीकरण है। इस मामले में अभिवाह प्रति इकाई क्षेत्र प्रति इकाई समय की संभावना है कि कण एक सतह से गुजरता है। सांतत्य समीकरण के अनुसार, इस अभिवाह का नकारात्मक विचलन संभाव्यता घनत्व के परिवर्तन की दर के बराबर है। सांतत्य समीकरण इस तथ्य को दर्शाता है कि अणु सदैव कहीं होता है - इसकी संभावना वितरण का समाकल अंग सदैव 1 के बराबर होता है - और यह एक निरंतर गति (कोई स्थानांतरणेशन) से चलता है।
क्वांटम यांत्रिकी
क्वांटम यांत्रिकी एक अन्य डोमेन है जहां संभाव्यता के संरक्षण से संबंधित एक सांतत्य समीकरण है। समीकरण में शर्तों के लिए निम्नलिखित परिभाषाओं की आवश्यकता होती है, और उपरोक्त अन्य उदाहरणों की तुलना में थोड़ा कम स्पष्ट है, इसलिए उन्हें यहां रेखांकित किया गया है:
- तरंग समारोह Ψ स्थिति और संवेग स्थान (बजाय स्थिति और संवेग स्थान) में एक कण के लिए, अर्थात स्थिति का एक कार्य r और समय t, Ψ = Ψ(r, t).
- प्रायिकता घनत्व फलन है
- कण के भीतर खोजने की संभावना V पर t द्वारा दर्शाया और परिभाषित किया गया है
- संभाव्यता वर्तमान (उर्फ संभाव्यता प्रवाह) है
इन परिभाषाओं के साथ सांतत्य समीकरण पढ़ता है:
The 3-d time dependent Schrödinger equation and its complex conjugate (i → −i throughout) are respectively:[4]
Multiplying the Schrödinger equation by Ψ* then solving for Ψ* ∂Ψ/∂t, and similarly multiplying the complex conjugated Schrödinger equation by Ψ then solving for Ψ ∂Ψ*/∂t;
substituting into the time derivative of ρ:
The Laplacian operators (∇2) in the above result suggest that the right hand side is the divergence of j, and the reversed order of terms imply this is the negative of j, altogether:
The integral form follows as for the general equation.
सेमीकंडक्टर
सेमीकंडक्टर में कुल करंट अभिवाह में प्रवाहकत्त्व बैंड और वैलेंस बैंड में छेद दोनों इलेक्ट्रॉनों के प्रवाहित होाव अभिवाह और प्रसार अभिवाह होते हैं।
एक आयाम में इलेक्ट्रॉनों के लिए सामान्य रूप:
- n इलेक्ट्रॉनों की स्थानीय सांद्रता है
- इलेक्ट्रॉन गतिशीलता है
- E रिक्तीकरण क्षेत्र में विद्युत क्षेत्र है
- डीnइलेक्ट्रॉनों के लिए प्रसार गुणांक है
- जीnइलेक्ट्रॉनों की पीढ़ी की दर है
- आरnइलेक्ट्रॉनों के पुनर्संयोजन की दर है
इसी तरह, छिद्रों के लिए:
- पी छिद्रों की स्थानीय सांद्रता है
- छिद्र गतिशीलता है
- E रिक्तीकरण क्षेत्र में विद्युत क्षेत्र है
- डीpछिद्रों के लिए प्रसार गुणांक है
- जीpछिद्रों के निर्माण की दर है
- आरpछिद्रों के पुनर्संयोजन की दर है
व्युत्पत्ति
यह खंड इलेक्ट्रॉनों के लिए उपरोक्त समीकरण की व्युत्पत्ति प्रस्तुत करता है। छिद्रों के समीकरण के लिए एक समान व्युत्पत्ति पाई जा सकती है।
इस तथ्य पर विचार करें कि एक्स-अक्ष के साथ क्रॉस-अनुभागीय क्षेत्र, ए, और लंबाई, डीएक्स के साथ अर्धचालक सामग्री की राशि में इलेक्ट्रॉनों की संख्या संरक्षित है। अधिक सटीक, कोई कह सकता है:
कुल इलेक्ट्रॉन वर्तमान घनत्व प्रवाहित होाव वर्तमान और प्रसार वर्तमान घनत्व का योग है:
समाधान
इन समीकरणों को वास्तविक उपकरणों में हल करने की कुंजी जब भी संभव हो ऐसे क्षेत्रों का चयन करना है जिनमें अधिकांश तंत्र नगण्य हैं ताकि समीकरण प्रवाहित होुत सरल रूप में कम हो जाएं।
सापेक्षतावादी संस्करण
विशेष सापेक्षता
विशेष सापेक्षता के अंकन और उपकरण, विशेष रूप से 4-सदिश और 4-ढाल, किसी भी सांतत्य समीकरण को लिखने का एक सुविधाजनक तरीका प्रदान करते हैं।
किसी राशि का घनत्व ρ और इसका करंट j को 4-सदिश में जोड़ा जा सकता है जिसे 4-वर्तमान कहा जाता है:
इस रूप में प्रायः लिखे जाने वाले सांतत्य समीकरणों के उदाहरणों में विद्युत आवेश संरक्षण सम्मिलित है
सामान्य सापेक्षता
सामान्य सापेक्षता में, जहां स्थान-समय घुमावदार होता है, ऊर्जा, आवेश या अन्य संरक्षित राशियों के लिए सांतत्य समीकरण (अंतर रूप में) में साधारण विचलन के बजाय सहसंयोजक व्युत्पन्न सम्मिलित होता है।
उदाहरण के लिए, तनाव-ऊर्जा टेंसर एक दूसरे क्रम का टेंसर क्षेत्र है जिसमें द्रव्यमान-ऊर्जा वितरण के ऊर्जा-संवेग घनत्व, ऊर्जा-संवेग अभिवाह और कतरनी तनाव होते हैं। सामान्य सापेक्षता में ऊर्जा-संवेग संरक्षण का अंतर रूप बताता है कि तनाव-ऊर्जा टेंसर का सहसंयोजक विचलन शून्य है:
परिणामस्वरूप, सांतत्य समीकरण के समाकल रूप को परिभाषित करना मुश्किल है और जरूरी नहीं कि उस क्षेत्र के लिए मान्य हो, जिसके भीतर स्पेसटाइम महत्वपूर्ण रूप से वक्रित हो (उदाहरण के लिए एक ब्लैक होल के आसपास, या पूरे ब्रह्मांड में)।[7]
कण भौतिकी
क्वार्क और ग्लून्स का रंग आवेश होता है, जो सदैव विद्युत आवेश की तरह संरक्षित होता है, और ऐसे रंग आवेश धाराओं के लिए एक सांतत्य समीकरण होता है (धाराओं के लिए स्पष्ट अभिव्यक्तियाँ ग्लूऑन क्षेत्र शक्ति टेंसर # गति के समीकरण में दी गई हैं)।
कण भौतिकी में कई अन्य राशि हैं जो प्रायः या सदैव संरक्षित होती हैं: बेरिऑन संख्या (क्वार्क की संख्या के अनुपात में प्रतिक्वार्क की संख्या को घटाकर), लेप्टान संख्या|इलेक्ट्रॉन संख्या, एमयू संख्या, ताऊ संख्या, समभारिक प्रचक्रण , और अन्य।[8] इनमें से प्रत्येक का संगत सांतत्य समीकरण है, संभवतः स्रोत/मंद शर्तों सहित।
नोएदर का प्रमेय
भौतिकी में प्रायः संरक्षण समीकरणों के होने का एक कारण नोएदर का प्रमेय है। यह बताता है कि जब भी भौतिकी के नियमों में निरंतर समरूपता होती है, तो कुछ संरक्षित भौतिक राशि के लिए एक सांतत्य समीकरण होता है। तीन सबसे प्रचलित उदाहरण हैं:
- समय अनुवाद के संबंध में भौतिकी के नियम अपरिवर्तनीय हैं | टाइम-ट्रांसलेशन- उदाहरण के लिए, भौतिकी के नियम आज भी वैसे ही हैं जैसे कल थे। यह समरूपता ऊर्जा के संरक्षण के लिए सांतत्य समीकरण की ओर ले जाती है।
- भौतिकी के नियम स्थान-अनुवाद के संबंध में अपरिवर्तनीय हैं- उदाहरण के लिए, ब्राजील में भौतिकी के नियम अर्जेंटीना में भौतिकी के नियमों के समान हैं। यह समरूपता गति के संरक्षण के लिए सांतत्य समीकरण की ओर ले जाती है।
- अभिविन्यास के संबंध में भौतिकी के नियम अपरिवर्तनीय हैं—उदाहरण के लिए, बाह्य स्थान में तैरते हुए, ऐसा कोई माप नहीं है जिससे आप यह कह सकें कि कौन सा मार्ग ऊपर की ओर है; आप कैसे उन्मुख हैं, भौतिकी के नियम समान हैं। यह समरूपता कोणीय गति के संरक्षण के लिए सांतत्य समीकरण की ओर ले जाती है।
यह भी देखें
- वन-वे वेव समीकरण
- संरक्षण नियम (भौतिकी)
- संरक्षण प्रपत्र
- अपव्यय प्रणाली
संदर्भ
- ↑ 1.0 1.1 Pedlosky, Joseph (1987). भूभौतिकीय द्रव गतिकी. Springer. pp. 10–13. ISBN 978-0-387-96387-7.
- ↑ Clancy, L.J.(1975), Aerodynamics, Section 3.3, Pitman Publishing Limited, London
- ↑ Fielding, Suzanne. "द्रव गतिकी की मूल बातें" (PDF). Durham University. Retrieved 22 December 2019.
- ↑ For this derivation see for example McMahon, D. (2006). Quantum Mechanics Demystified. McGraw Hill. ISBN 0-07-145546-9.
- ↑ D. McMahon (2006). रिलेटिविटी डीमिस्टीफाइड. McGraw Hill (USA). ISBN 0-07-145545-0.
- ↑ C.W. Misner; K.S. Thorne; J.A. Wheeler (1973). आकर्षण-शक्ति. W.H. Freeman & Co. ISBN 0-7167-0344-0.
- ↑ Michael Weiss; John Baez. "Is Energy Conserved in General Relativity?". Retrieved 2014-04-25.
- ↑ J.A. Wheeler; C. Misner; K.S. Thorne (1973). आकर्षण-शक्ति. W.H. Freeman & Co. pp. 558–559. ISBN 0-7167-0344-0.
अग्रिम पठन
- Hydrodynamics, H. Lamb, Cambridge University Press, (2006 digitalization of 1932 6th edition) ISBN 978-0-521-45868-9
- Introduction to Electrodynamics (3rd Edition), D.J. Griffiths, Pearson Education Inc, 1999, ISBN 81-7758-293-3
- Electromagnetism (2nd edition), I.S. Grant, W.R. Phillips, Manchester Physics Series, 2008 ISBN 0-471-92712-0
- Gravitation, J.A. Wheeler, C. Misner, K.S. Thorne, W.H. Freeman & Co, 1973, ISBN 0-7167-0344-0