गोलाई

परिणाम के एक समारोह का ग्राफ, y, गोलाई का x विभिन्न विधियों का उपयोग करना। स्पष्टता के लिए, रेखांकन को पूर्णांक से विस्थापित दिखाया गया है y मान। एसवीजी फ़ाइल में, इसे हाइलाइट करने के लिए एक विधि पर होवर करें और सिंक्रनाइज़ मल्टीमीडिया एकीकरण भाषा ब्राउज़र में, इसे चुनने या अचयनित करने के लिए क्लिक करें।

राउंडिंग का अर्थ है किसी संख्या को सन्निकटन मान से बदलना जिसका छोटा, सरल या अधिक स्पष्ट प्रतिनिधित्व हो। उदाहरण के लिए, $ की जगह23.4476 $ के साथ23.45, अंश 312/937 के साथ 1/3, या व्यंजक √2 साथ 1.414.

राउंडिंग अक्सर एक मूल्य प्राप्त करने के लिए किया जाता है जो मूल की तुलना में रिपोर्ट करना और संचार करना आसान होता है। गणना संख्या, माप, या अनुमान की झूठी सटीक रिपोर्टिंग से बचने के लिए गोलाई भी महत्वपूर्ण हो सकती है; उदाहरण के लिए, एक मात्रा जिसकी गणना की गई थी 123,456 लेकिन केवल कुछ सौ इकाइयों के भीतर सटीकता और सटीकता के लिए जाना जाता है, आमतौर पर इसके बारे में बेहतर कहा जाता है 123,500 .

दूसरी ओर, सटीक संख्याओं की राउंडिंग रिपोर्ट किए गए परिणाम में कुछ राउंड-ऑफ़ त्रुटि पेश करेगी। कई संगणनाओं की रिपोर्ट करते समय गोलाई लगभग अपरिहार्य है - विशेषकर जब दो संख्याओं को पूर्णांक या निश्चित-बिंदु अंकगणित में विभाजित किया जाता है; गणितीय कार्यों जैसे कि वर्गमूल, लघुगणक और साइन की गणना करते समय; या फ़्लोटिंग-पॉइंट अंकगणित का उपयोग करते समय | फ़्लोटिंग-पॉइंट प्रतिनिधित्व एक निश्चित संख्या में महत्वपूर्ण अंकों के साथ। गणनाओं के एक क्रम में, ये राउंडिंग त्रुटियां आम तौर पर अनिश्चितता का प्रसार करती हैं, और कुछ बीमार स्थितियों में वे परिणाम को अर्थहीन बना सकती हैं।

पारलौकिक समारोह का सटीक राउंडिंग मुश्किल है क्योंकि अतिरिक्त अंकों की संख्या को हल करने के लिए गणना करने की आवश्यकता है कि क्या ऊपर या नीचे राउंड करना है या नहीं, पहले से ज्ञात नहीं किया जा सकता है। इस समस्या को #टेबल-मेकर की दुविधा|टेबल-मेकर की दुविधा के रूप में जाना जाता है।

राउंडिंग में क्वांटिज़ेशन (सिग्नल प्रोसेसिंग) के लिए कई समानताएं होती हैं जो तब होती हैं जब भौतिक मात्रा को संख्याओं या डिजिटल सिग्नल (सिग्नल प्रोसेसिंग) द्वारा एन्कोड किया जाना चाहिए।

A लगभग बराबर का चिह्न (<बड़ा>≈</बड़ा>: लगभग बराबर) का उपयोग कभी-कभी सटीक संख्याओं के पूर्णांकन को इंगित करने के लिए किया जाता है, उदाहरण के लिए, 9.98 ≈ 10. यह चिन्ह 1892 में अल्फ्रेड जॉर्ज ग्रीनहिल द्वारा पेश किया गया था।^[1] राउंडिंग विधियों की आदर्श विशेषताओं में शामिल हैं:

राउंडिंग एक फंक्शन (गणित) द्वारा की जानी चाहिए। इस तरह, जब एक ही इनपुट को अलग-अलग उदाहरणों में गोल किया जाता है, तो आउटपुट अपरिवर्तित रहता है।
राउंडिंग के साथ की गई गणना राउंडिंग के बिना की गई गणनाओं के करीब होनी चाहिए।
- (1) और (2) के परिणामस्वरूप, राउंडिंग से आउटपुट इसके इनपुट के करीब होना चाहिए, अक्सर कुछ मीट्रिक (गणित) द्वारा जितना संभव हो उतना करीब।
राउंडिंग पर विचार करने के लिए, फ़ंक्शन की श्रेणी सामान्य असतत सेट में फ़ंक्शन के डोमेन का सबसेट होगी। एक शास्त्रीय सीमा पूर्णांक, पूर्णांक है।
राउंडिंग को गणित में समरूपता को बनाए रखना चाहिए जो पहले से ही डोमेन और रेंज के बीच मौजूद है। परिमित परिशुद्धता (या असतत डोमेन) के साथ, यह पूर्वाग्रह (सांख्यिकी) को हटाने के लिए अनुवाद करता है।
राउंडिंग विधि की कंप्यूटर विज्ञान या मानव अंकगणित में उपयोगिता होनी चाहिए जहां परिमित सटीकता का उपयोग किया जाता है, और गति एक विचार है।

क्योंकि सभी आदर्श विशेषताओं को पूरा करने के लिए एक विधि के लिए आम तौर पर संभव नहीं है, कई अलग-अलग राउंडिंग विधियां मौजूद हैं।

एक सामान्य नियम के रूप में, गोलाई करना आलस्य है;^[2] यानी, एक बार किसी संख्या को गोल करने के बाद, उसे फिर से गोल करने से उसका मान नहीं बदलेगा। राउंडिंग फ़ंक्शन भी मोनोटोनिक फ़ंक्शन हैं; अर्थात।, rounding a larger number gives a larger or equal result than rounding a smaller number^{[clarification needed]}. असतत श्रेणी के सामान्य मामले में, वे टुकड़े-टुकड़े स्थिर कार्य होते हैं।

गोलाई के प्रकार

विशिष्ट गोलाई समस्याओं में शामिल हैं:

Rounding problem	Example input	Result	Rounding criterion
Approximating an irrational number by a fraction	[[pi\| $π$ ]]	22 / 7	1-digit-denominator
Approximating a rational number by another fraction with smaller numerator and denominator	399 / 941	3 / 7	1-digit-denominator
Approximating a fraction, which have periodic decimal expansion, by a finite decimal fraction	5 / 3	1.6667	4 decimal places
Approximating a fractional decimal number by one with fewer digits	2.1784	2.18	2 decimal places
Approximating a decimal integer by an integer with more trailing zeros	23,217	23,200	3 significant figures
Approximating a large decimal integer using scientific notation	300,999,999	3.01 × 10⁸	3 significant figures
Approximating a value by a multiple of a specified amount	48.2	45	Multiple of 15
Rounding each one of a finite set of real numbers (mostly fractions) to an integer (sometimes the second-nearest integer) so that the sum of the rounded numbers equals the rounded sum of the numbers (needed e.g. [1] for the apportionment of seats, implemented e.g. by the largest remainder method, see Mathematics of apportionment, and [2] for distributing the total VAT of an invoice to its items)	{3/12, 4/12, 5/12}	{0, 0, 1}	Sum of rounded elements equals rounded sum of elements

पूर्णांक के लिए गोलाई

राउंडिंग का सबसे बुनियादी रूप एक मनमानी संख्या को पूर्णांक से बदलना है। निम्नलिखित सभी राउंडिंग मोड एक सार एकल-तर्क राउंड () प्रक्रिया के ठोस कार्यान्वयन हैं। ये सच्चे कार्य हैं (उन लोगों के अपवाद के साथ जो यादृच्छिकता का उपयोग करते हैं)।

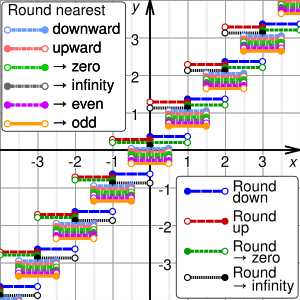
एक पूर्णांक पर निर्देशित गोलाई

मूल संख्या से विस्थापन के रूप में इन चार विधियों को निर्देशित गोलाई कहा जाता है x गोल मान के लिए y सभी एक ही सीमित मान (0, विस्तारित वास्तविक संख्या रेखा|+∞, या −∞) की ओर या उससे दूर निर्देशित हैं। डायरेक्टेड राउंडिंग का उपयोग अंतराल अंकगणित में किया जाता है और अक्सर वित्तीय गणनाओं में इसकी आवश्यकता होती है।

अगर x पॉजिटिव है, राउंड-डाउन राउंड-टू-जीरो के समान है, और राउंड-अप राउंड-अवे-फ्रॉम-जीरो के समान है। अगर x नेगेटिव है, राउंड-डाउन शून्य से राउंड-अवे के समान है, और राउंड-अप राउंड-टू-जीरो के समान है। किसी भी मामले में, अगर x एक पूर्णांक है, y बस है x.

जहां कई गणनाएं क्रम में की जाती हैं, वहां राउंडिंग पद्धति का चुनाव परिणाम पर बहुत महत्वपूर्ण प्रभाव डाल सकता है। एक प्रसिद्ध उदाहरण में 1982 में वैंकूवर स्टॉक एक्सचेंज द्वारा स्थापित एक नया स्टॉक सूची शामिल था। इसे शुरू में 1000.000 (सटीकता के तीन दशमलव स्थान) पर सेट किया गया था, और 22 महीनों के बाद लगभग 520 तक गिर गया था - जबकि स्टॉक की कीमतें आम तौर पर 1982 में बढ़ी थीं। अवधि। समस्या का कारण यह था कि सूचकांक को प्रतिदिन हजारों बार पुनर्गणना किया जाता था, और हमेशा 3 दशमलव स्थानों तक गोल किया जाता था, इस तरह से गोल करने वाली त्रुटियां जमा हो जाती थीं। बेहतर राउंडिंग के साथ पुनर्गणना करने पर इसी अवधि के अंत में 1098.892 का इंडेक्स वैल्यू मिला।^[3] नीचे दिए गए उदाहरणों के लिए, $sgn(x)$ मूल संख्या पर लागू साइन समारोह को संदर्भित करता है, $x$ .

नीचे घूमना

राउंड डाउन (या फर्श और छत के कार्य लें, या नेगेटिव इनफिनिटी की ओर राउंड करें): y सबसे बड़ा पूर्णांक है जो इससे अधिक नहीं है x.
$y=\mathrm {floor} (x)=\left\lfloor x\right\rfloor =-\left\lceil -x\right\rceil$

उदाहरण के लिए, 23.7 को 23 में बदल दिया जाता है, और -23.2 को -24 में बदल दिया जाता है।

राउंडिंग अप

गोल करें (या फर्श और छत के कार्यों को लें, या सकारात्मक अनंतता की ओर गोल करें): y सबसे छोटा पूर्णांक है जो इससे कम नहीं है x.
$y=\operatorname {ceil} (x)=\left\lceil x\right\rceil =-\left\lfloor -x\right\rfloor$

उदाहरण के लिए, 23.2 को 24 में बदल दिया जाता है, और -23.7 को -23 में बदल दिया जाता है।

शून्य की ओर घूमना

शून्य की ओर गोल (या काट-छांट , या अनंत से दूर गोल): y वह पूर्णांक है जो निकटतम है x जैसे कि यह 0 और के बीच है x (शामिल); अर्थात। y का पूर्णांक भाग है x, इसके अंश अंकों के बिना।
$y=\operatorname {truncate} (x)=\operatorname {sgn}(x)\left\lfloor \left|x\right|\right\rfloor =-\operatorname {sgn}(x)\left\lceil -\left|x\right|\right\rceil ={\begin{cases}\left\lfloor x\right\rfloor &x\geq 0\\\left\lceil x\right\rceil &x<0\\\end{cases}}$

उदाहरण के लिए, 23.7 को 23 में बदल दिया जाता है, और -23.7 को -23 में बदल दिया जाता है।

शून्य से दूर घूमना

शून्य से दूर (या अनंत की ओर गोल): y वह पूर्णांक है जो 0 के सबसे निकट है (या समतुल्य, to x) ऐसा है कि x 0 और के बीच है y (शामिल)।
$y=\operatorname {sgn}(x)\left\lceil \left|x\right|\right\rceil =-\operatorname {sgn}(x)\left\lfloor -\left|x\right|\right\rfloor ={\begin{cases}\left\lceil x\right\rceil &x\geq 0\\\left\lfloor x\right\rfloor &x<0\\\end{cases}}$

उदाहरण के लिए, 23.2 को 24 में बदल दिया जाता है, और -23.2 को -24 में बदल दिया जाता है।

निकटतम पूर्णांक तक पूर्णांक बनाना

किसी संख्या को गोल करना x निकटतम पूर्णांक के लिए उन मामलों के लिए कुछ टाई-ब्रेकिंग नियम की आवश्यकता होती है जब x दो पूर्णांकों के बीच बिल्कुल आधा-अधूरा है - यानी, जब का अंश भाग x ठीक 0.5 है।

यदि यह 0.5 भिन्नात्मक भागों के लिए नहीं था, तो राउंड-ऑफ़ त्रुटियों को राउंड टू निकटतम विधि द्वारा पेश किया गया सममित होगा: प्रत्येक अंश के लिए जो नीचे गोल हो जाता है (जैसे 0.268), एक पूरक अंश होता है (अर्थात्, 0.732) समान राशि से पूर्णांकित हो जाता है।

असतत समान वितरण आंशिक भागों के साथ निश्चित-बिंदु अंकगणित के एक बड़े सेट को गोल करते समय, सभी मानों द्वारा गोल करने वाली त्रुटियां, 0.5 भिन्नात्मक भाग वाले लोगों की चूक के साथ, सांख्यिकीय रूप से एक-दूसरे की भरपाई करेंगे। इसका मतलब यह है कि राउंडेड नंबरों का अपेक्षित मूल्य | अनुमानित (औसत) मूल्य मूल संख्याओं के अपेक्षित मूल्य के बराबर होता है जब सेट से आंशिक भाग 0.5 वाली संख्या हटा दी जाती है।

व्यवहार में, फ़्लोटिंग-पॉइंट अंकगणित | फ़्लोटिंग-पॉइंट नंबर आमतौर पर उपयोग किए जाते हैं, जिनमें और भी अधिक कम्प्यूटेशनल बारीकियाँ होती हैं क्योंकि वे समान दूरी पर नहीं होते हैं।

आधा चक्कर लगाना

निम्नलिखित टाई-ब्रेकिंग नियम, जिसे राउंड हाफ अप (या राउंड हाफ पॉजिटिव इन्फिनिटी की ओर) कहा जाता है, कई विषयों में व्यापक रूप से उपयोग किया जाता है।^{[citation needed]} अर्थात्, के आधे-अधूरे मान x हमेशा गोलाकार होते हैं।

यदि का भिन्नात्मक भाग x ठीक 0.5 है, तो y = x + 0.5
$y=\left\lfloor x+0.5\right\rfloor =-\left\lceil -x-0.5\right\rceil =\left\lceil {\frac {\lfloor 2x\rfloor }{2}}\right\rceil$

उदाहरण के लिए, 23.5 को 24 में बदल दिया जाता है, और -23.5 को -23 में बदल दिया जाता है।

हालाँकि, कुछ प्रोग्रामिंग लैंग्वेज (जैसे कि जावा, पायथन) अपने हाफ अप को शून्य से आधे दूर #Rounding के रूप में परिभाषित करती हैं।^[4]^[5] इस पद्धति में दो के पूरक और समान अभ्यावेदन में गोल करने की दिशा निर्धारित करने के लिए केवल एक अंक की जाँच की आवश्यकता होती है।

आधा नीचे चक्कर लगाना

अधिक सामान्य 'राउंड हाफ अप' के विपरीत कोई भी राउंड हाफ डाउन (या नेगेटिव इनफिनिटी की ओर राउंड हाफ) का उपयोग कर सकता है।

यदि का भिन्नात्मक भाग x ठीक 0.5 है, तो y = x − 0.5
$y=\left\lceil x-0.5\right\rceil =-\left\lfloor -x+0.5\right\rfloor =\left\lfloor {\frac {\lceil 2x\rceil }{2}}\right\rfloor$

उदाहरण के लिए, 23.5 को 23 में बदल दिया जाता है, और -23.5 को -24 में बदल दिया जाता है।

हालाँकि, कुछ प्रोग्रामिंग लैंग्वेज (जैसे जावा, पायथन) ने अपने हाफ डाउन को #Rounding half को शून्य की ओर परिभाषित किया है।^[4]^[5]

आधे को शून्य की ओर घुमाना

परंपरागत शून्य से आधा दूर गोल के विपरीत आधा शून्य की ओर (या अनंत से आधा दूर गोल) भी गोल हो सकता है।

यदि का भिन्नात्मक भाग x ठीक 0.5 है, तो y = x − 0.5 अगर x सकारात्मक है, और y = x + 0.5 अगर x ऋणात्मक है।
$y=\operatorname {sgn}(x)\left\lceil \left|x\right|-0.5\right\rceil =-\operatorname {sgn}(x)\left\lfloor -\left|x\right|+0.5\right\rfloor$

उदाहरण के लिए, 23.5 को 23 में बदल दिया जाता है, और -23.5 को -23 में बदल दिया जाता है।

यह विधि सकारात्मक और नकारात्मक मानों को सममित रूप से व्यवहार करती है, और इसलिए समग्र सकारात्मक / नकारात्मक पूर्वाग्रह से मुक्त होती है यदि मूल संख्या समान संभावना के साथ सकारात्मक या नकारात्मक हो। हालाँकि, यह अभी भी शून्य की ओर पूर्वाग्रह रखता है।

शून्य से आधा चक्कर लगाना

अन्य टाई-ब्रेकिंग विधि जो आमतौर पर सिखाई और उपयोग की जाती है, वह शून्य से आधी दूरी पर गोल (या अनंत की ओर आधा चक्कर) है, अर्थात्:

यदि का भिन्नात्मक भाग x ठीक 0.5 है, तो y = x + 0.5 अगर x सकारात्मक है, और y = x − 0.5 अगर x ऋणात्मक है।
$y=\operatorname {sgn}(x)\left\lfloor \left|x\right|+0.5\right\rfloor =-\operatorname {sgn}(x)\left\lceil -\left|x\right|-0.5\right\rceil$

उदाहरण के लिए, 23.5 को 24 में बदल दिया जाता है, और -23.5 को -24 में बदल दिया जाता है।

यह बाइनरी कंप्यूटर पर अधिक कुशल हो सकता है क्योंकि यह निर्धारित करने के लिए कि क्या यह ऊपर (1 पर) या नीचे (0 पर) राउंड करता है, केवल पहले छोड़े गए बिट पर विचार करने की आवश्यकता है। यह एक ऐसी विधि है जिसका उपयोग इसकी सरलता के कारण सार्थक अंकों तक सन्निकटित करते समय किया जाता है।

यह विधि, जिसे कमर्शियल राउंडिंग के रूप में भी जाना जाता है,^{[citation needed]} सकारात्मक और नकारात्मक मानों को सममित रूप से व्यवहार करता है, और इसलिए समग्र सकारात्मक/नकारात्मक पूर्वाग्रह से मुक्त होता है यदि मूल संख्या समान संभावना के साथ सकारात्मक या नकारात्मक हो। हालाँकि, यह अभी भी शून्य से पूर्वाग्रह दूर है।

इसका उपयोग अक्सर मुद्रा रूपांतरण और मूल्य राउंडिंग के लिए किया जाता है (जब राशि को पहली बार मुद्रा के सबसे छोटे महत्वपूर्ण उपखंड में परिवर्तित किया जाता है, जैसे कि यूरो के सेंट) क्योंकि पूरक के स्वतंत्र रूप से केवल पहले भिन्नात्मक अंक पर विचार करके व्याख्या करना आसान है। सटीक अंक या राशि का संकेत (राशि के भुगतान और प्राप्तकर्ता के बीच सख्त समानता के लिए)।

आधा से सम तक चक्कर लगाना

सकारात्मक/नकारात्मक पूर्वाग्रह के बिना और शून्य से आगे/दूर पूर्वाग्रह के बिना एक टाई-ब्रेकिंग नियम 'राउंड हाफ टू ईवन' है। इस परिपाटी द्वारा, यदि का भिन्नात्मक भाग x 0.5 है, तो y निकटतम सम पूर्णांक है x. इस प्रकार, उदाहरण के लिए, +23.5 +24 बन जाता है, जैसा कि +24.5 होता है; हालांकि, -23.5 -24 बन जाता है, जैसा कि -24.5 होता है। यह फ़ंक्शन अनुमानित त्रुटि को कम करता है जब गोल आंकड़ों का योग करते हैं, तब भी जब इनपुट अधिकतर सकारात्मक या अधिकतर नकारात्मक होते हैं, बशर्ते वे न तो अधिकतर और न ही अधिकतर विषम हों।

राउंड-टू-निकटतम विधि के इस संस्करण को अभिसारी राउंडिंग, सांख्यिकीविद की राउंडिंग, डच राउंडिंग, गॉसियन राउंडिंग, ऑड-ईवन राउंडिंग भी कहा जाता है।^[6] या बैंकरों की गोलाई।

यह बाइनरी फ़्लोटिंग-पॉइंट स्वरूपों में परिणामों के लिए IEEE 754 संचालन में उपयोग किया जाने वाला डिफ़ॉल्ट राउंडिंग मोड है, और the more sophisticated mode^{[clarification needed]} सार्थक अंकों तक राउंडिंग करते समय उपयोग किया जाता है।

पूर्वाग्रह को समाप्त करके, स्वतंत्र संख्याओं का बार-बार जोड़ या घटाव, जैसा कि रैंडम वॉक#वन-डायमेंशनल रैंडम वॉक|वन-डायमेंशनल रैंडम वॉक में होता है, एक त्रुटि के साथ एक गोल परिणाम देगा जो वर्गमूल के अनुपात में बढ़ने की प्रवृत्ति रखता है रैखिक के बजाय संचालन की संख्या।

हालाँकि, यह नियम ऑड्स के सापेक्ष ईवन्स की संभावना को बढ़ाकर वितरण को विकृत करता है। आमतौर पर यह कम महत्वपूर्ण होता है^{[citation needed]} इस पद्धति से समाप्त होने वाले पूर्वाग्रहों की तुलना में।

आधा को विषम में सन्निकटित करना

राउंड हाफ टू ईवन के लिए समान टाई-ब्रेकिंग नियम राउंड हाफ टू ऑड है। इस दृष्टिकोण में, यदि का भिन्नात्मक भाग x 0.5 है, तो y निकटतम विषम पूर्णांक है x. इस प्रकार, उदाहरण के लिए, +23.5 +23 बन जाता है, जैसा कि +22.5 करता है; जबकि -23.5 -23 बन जाता है, जैसा कि -22.5 होता है।

यह विधि सकारात्मक/नकारात्मक पूर्वाग्रह और शून्य से दूर/दूर पूर्वाग्रह से भी मुक्त है, बशर्ते कि गोल की जाने वाली संख्या न तो अधिकतर और न ही अधिकतर विषम हो। यह मूल वितरण को विकृत करने के लिए गोल आधे से सम गुण को भी साझा करता है, क्योंकि यह सम के सापेक्ष बाधाओं की संभावना को बढ़ाता है।

इस संस्करण का लगभग कभी भी संगणना में उपयोग नहीं किया जाता है, सिवाय उन स्थितियों के जहां कोई फ़्लोटिंग-पॉइंट नंबरों के पैमाने को बढ़ाने से बचना चाहता है, जिसकी एक सीमित घातांक सीमा होती है। गोल आधे से सम तक, एक गैर-अनंत संख्या अनंत के लिए गोल होगी, और एक छोटी denormal मान सामान्य गैर-शून्य मान पर होगा। प्रभावी रूप से, यह मोड समान मूलांक (जैसे बाइनरी और दशमलव) के अंक प्रणालियों के लिए संभव होने पर आउट-ऑफ़-रेंज परिणामों से बचने के लिए टाई नंबरों के मौजूदा पैमाने को संरक्षित करना पसंद करता है।^{[clarification needed (see talk)]}

कम परिशुद्धता के लिए तैयार करने के लिए गोलाई

राउंडिंग मोड (इस अध्याय में आरपीएसपी) का उपयोग #डबल राउंडिंग (मल्टीपल सहित) राउंडिंग के साथ गलत परिणाम प्राप्त करने से बचने के लिए किया जाता है। इस राउंडिंग मोड के साथ, डबल राउंडिंग के बाद गलत परिणाम से बचा जा सकता है, यदि फाइनल राउंडिंग को छोड़कर सभी राउंडिंग RPSP का उपयोग करके की जाती हैं, और केवल फाइनल राउंडिंग बाहरी रूप से अनुरोधित मोड का उपयोग करती है।

दशमलव अंकगणित के साथ, यदि सबसे छोटे महत्वपूर्ण अंक 0 या 1, 4 या 5, 5 या 6, 9 या 0 के बीच कोई विकल्प है, तो 0 या 5 से भिन्न अंक का चयन किया जाएगा; अन्यथा, चुनाव मनमाना है। आईबीएम परिभाषित करता है ^[7] बाद वाले मामले में, छोटे परिमाण वाले अंक का चयन किया जाएगा। RPSP को दो परिणामी राउंडिंग के बीच एक अंक के रूप में छोटा किया जा सकता है (उदाहरण के लिए, 1/10 तक राउंडिंग को 1/100 तक राउंडिंग के बाद लागू किया जा सकता है)। उदाहरण के लिए, जब पूर्णांक में गोल किया जाता है,

20.0 को 20 में बदल दिया गया है;
20.01, 20.1, 20.9, 20.99, 21, 21.01, 21.9, 21.99 को 21 में बदल दिया गया है;
22.0, 22.1, 22.9, 22.99 को 22 में बदल दिया गया है;
24.0, 24.1, 24.9, 24.99 को 24 में बदल दिया गया है;
25.0 को 25 में बदल दिया गया है;
25.01, 25.1 को 26 में बदल दिया गया है।

डबल राउंडिंग सेक्शन के उदाहरण में, 9.46 को एक दशमलव तक राउंड करने पर 9.4 मिलता है, जो बदले में पूर्णांक तक राउंडिंग 9 देता है।

बाइनरी अंकगणित के साथ, राउंडिंग को राउंड टू ऑड के रूप में बनाया जाता है (#Rounding हाफ से ऑड के साथ मिश्रित नहीं किया जाना चाहिए।) उदाहरण के लिए, जब 1/4 पर राउंडिंग किया जाता है:

x == 2.0 => परिणाम 2 है
2.0 < x < 2.5 => परिणाम 2.25 है
x == 2.5 => परिणाम 2.5 है
2.5 < x < 3.0 => परिणाम 2.75 है
x == 3.0 => परिणाम 3.0 है

सही परिणामों के लिए, RPSP को कम से कम 2 बाइनरी अंकों के चरण के साथ लागू किया जाएगा, अन्यथा गलत परिणाम दिखाई दे सकता है। उदाहरण के लिए,

3.125 आरपीएसपी से 1/4 => परिणाम 3.25 है
3.25 आरपीएसपी से 1/2 => परिणाम 3.5 है
3.5 राउंड-हाफ-टू-ईवन टू 1 => परिणाम 4 (गलत) है

यदि चरण 2 बिट या अधिक है, तो RPSP 3.25 देता है, जो बदले में, 3 में पूर्णांक परिणाम के लिए राउंड-हाफ-टू-ईवन देता है।

RPSP को IBM zSeries और pSeries में हार्डवेयर में लागू किया गया है।

एक पूर्णांक के लिए रैंडम राउंडिंग

वैकल्पिक टाई-ब्रेकिंग

एक विधि, सबसे अधिक अस्पष्ट, 0.5 भिन्नात्मक भाग के साथ एक संख्या को गोल करते समय वैकल्पिक दिशा है। अन्य सभी को निकटतम पूर्णांक तक गोल किया गया है।

जब भी भिन्नात्मक भाग 0.5 हो, बारी-बारी से ऊपर या नीचे घुमाएँ: 0.5 भिन्नात्मक भाग की पहली घटना के लिए, गोल ऊपर, दूसरी घटना के लिए, गोल नीचे, और इसी तरह। वैकल्पिक रूप से, पहले 0.5 भिन्नात्मक भाग की गोलाई को एक यादृच्छिक बीज द्वारा निर्धारित किया जा सकता है। ऊपर और नीचे कोई भी दो राउंडिंग विधियां हो सकती हैं जो एक दूसरे का विरोध करती हैं - सकारात्मक अनंतता की ओर और दूर या शून्य से दूर और दूर।

यदि 0.5 भिन्नात्मक भागों की घटनाएँ घटना की गिनती के पुनः आरंभ होने की तुलना में महत्वपूर्ण रूप से अधिक होती हैं, तो यह प्रभावी रूप से पूर्वाग्रह मुक्त है। गारंटीकृत शून्य पूर्वाग्रह के साथ, यह उपयोगी है यदि संख्याओं का योग या औसत किया जाए।

रैंडम टाई-ब्रेकिंग

यदि का भिन्नात्मक भाग x 0.5 है, चुनें y बेतरतीब ढंग से के बीच x + 0.5 और x − 0.5, समान संभावना के साथ। अन्य सभी को निकटतम पूर्णांक तक गोल किया गया है।

राउंड-हाफ-टू-ईवन और राउंड-हाफ-टू-ऑड की तरह, यह नियम अनिवार्य रूप से समग्र पूर्वाग्रह से मुक्त है, लेकिन यह सम और विषम के बीच भी उचित है y मान। वैकल्पिक टाई-ब्रेकिंग पर एक फायदा यह है कि 0.5 भिन्नात्मक भाग पर गोलाई की अंतिम दिशा को याद नहीं रखना पड़ता है।

स्टोकेस्टिक राउंडिंग

नकारात्मक अनंत की ओर निकटतम पूर्णांक में से एक के रूप में और सकारात्मक अनंत की ओर निकटतम पूर्णांक के रूप में, निकटता पर निर्भर संभाव्यता के साथ राउंडिंग को स्टोचैस्टिक राउंडिंग कहा जाता है और यह औसत पर एक निष्पक्ष परिणाम देगा।^[8]

\operatorname {Round} (x)={\begin{cases}\lfloor x\rfloor &{\text{ with probability }}1-(x-\lfloor x\rfloor )=\lfloor x\rfloor -x+1\\\lfloor x\rfloor +1&{\text{ with probability }}{x-\lfloor x\rfloor }\end{cases}}

उदाहरण के लिए, 1.6 को प्रायिकता 0.4 के साथ 1 और प्रायिकता 0.6 के साथ 2 तक राउंड किया जाएगा।

स्टोचैस्टिक राउंडिंग एक तरह से सटीक हो सकती है कि राउंडिंग फ़ंक्शन (गणित) कभी नहीं हो सकता। उदाहरण के लिए, मान लीजिए कि किसी ने 0 से शुरू किया और प्रत्येक जोड़ के बीच रनिंग टोटल को गोल करते हुए उसमें 0.3 को एक सौ बार जोड़ दिया। परिणाम नियमित राउंडिंग के साथ 0 होगा, लेकिन स्टोकेस्टिक राउंडिंग के साथ, अपेक्षित परिणाम 30 होगा, जो बिना राउंडिंग के प्राप्त समान मूल्य है। यह यंत्र अधिगम में उपयोगी हो सकता है जहां प्रशिक्षण कम सटीक अंकगणित का पुनरावृत्त रूप से उपयोग कर सकता है।^[8]स्टोचैस्टिक राउंडिंग भी 1-आयामी कटौती प्राप्त करने का एक तरीका है।

एक पूर्णांक तक पूर्णांक बनाने के लिए दृष्टिकोणों की तुलना

Value	Functional methods											Randomized methods
	Directed rounding				Round to nearest						Round to prepare for shorter precision	Alternating tie-break		Random tie-break		Stochastic
	Down (toward −∞)	Up (toward +∞)	Toward 0	Away From 0	Half Down (toward −∞)	Half Up (toward +∞)	Half Toward 0	Half Away From 0	Half to Even	Half to Odd	Round to prepare for shorter precision	Average	SD	Average	SD	Average	SD
+1.8	+1	+2	+1	+2	+2	+2	+2	+2	+2	+2	+1	+2	0	+2	0	+1.8	0.04
+1.5					+1	+2	+1	+2	+2	+1		+1.505	0	+1.5	0.05	+1.5	0.05
+1.2						+1		+1	+1			+1	0	+1	0	+1.2	0.04
+0.8	0	+1	0	+1					+1			+1	0	+1	0	+0.8	0.04
+0.5					0		0		0			+0.505	0	+0.5	0.05	+0.5	0.05
+0.2						0		0		0		0	0	0	0	+0.2	0.04
−0.2	−1	0		−1				0		0	−1	0	0	0	0	−0.2	0.04
−0.5					−1			−1		−1		−0.495	0	−0.5	0.05	−0.5	0.05
−0.8						−1	−1		−1			−1	0	−1	0	−0.8	0.04
−1.2	−2	−1	−1	−2					−1			−1	0	−1	0	−1.2	0.04
−1.5					−2			−2	−2			−1.495	0	−1.5	0.05	−1.5	0.05
−1.8					−2	−2	−2	−2	−2	−2		−2	0	−2	0	−1.8	0.04

अन्य मूल्यों के लिए चक्कर लगाना

एक निर्दिष्ट गुणक में पूर्णांक बनाना

राउंडिंग का सबसे सामान्य प्रकार एक पूर्णांक तक राउंड करना है; या, अधिक आम तौर पर, कुछ वेतन वृद्धि के एक पूर्णांक गुणक के लिए - जैसे कि सेकंड के पूरे दसवें हिस्से में, डॉलर के सौवें हिस्से में, 1/2 या 1/8 इंच के पूरे गुणकों में, पूरे दर्जनों या हजारों में, आदि।

सामान्य तौर पर, एक संख्या को गोल करना x कुछ निर्दिष्ट धनात्मक मान के गुणज में m में निम्नलिखित चरण शामिल हैं:

\mathrm {roundToMultiple} (x,m)=\mathrm {round} (x/m)\times m

उदाहरण के लिए, गोलाई x = 2.1784 डॉलर पूरे सेंट (यानी, 0.01 के गुणक के लिए) में 2.1784/0.01=217.84 की गणना की जाती है, फिर इसे 218 तक गोल किया जाता है, और अंत में 218×0.01=2.18 की गणना की जाती है।

जब महत्वपूर्ण अंकों की पूर्व निर्धारित संख्या में पूर्णांकन किया जाता है, तो वृद्धि m गोल की जाने वाली संख्या (या गोल परिणाम) के परिमाण पर निर्भर करता है।

वृद्धि m संख्याओं का प्रतिनिधित्व करने के लिए जो भी अंक प्रणाली का उपयोग किया जाता है, उसमें सामान्य रूप से एक परिमित अंश होता है। मनुष्यों को प्रदर्शित करने के लिए, आमतौर पर इसका अर्थ दशमलव (अर्थात, m 10 की एक शक्ति (गणित) का पूर्णांक गुणा है, जैसे 1/1000 या 25/100)। डिजिटल कंप्यूटरों में संग्रहीत मध्यवर्ती मानों के लिए, इसका अर्थ अक्सर बाइनरी संख्या (m एक पूर्णांक गुणा 2 की शक्ति है)।

सार एकल-तर्क राउंड () फ़ंक्शन जो एक मनमाना वास्तविक मान से एक पूर्णांक देता है, में कम से कम एक दर्जन विशिष्ट ठोस परिभाषाएँ #Rounding से पूर्णांक अनुभाग में प्रस्तुत की गई हैं। अमूर्त दो-तर्क राउंडटूमल्टीपल () फ़ंक्शन को औपचारिक रूप से यहां परिभाषित किया गया है, लेकिन कई मामलों में इसका उपयोग निहित मूल्य के साथ किया जाता है m = 1 वेतन वृद्धि के लिए और फिर समान दर्जन विशिष्ट ठोस परिभाषाओं के साथ समकक्ष सार एकल-तर्क फ़ंक्शन को कम करता है।

लॉगरिदमिक राउंडिंग

एक निर्दिष्ट शक्ति तक चक्कर लगाना

निर्दिष्ट घात पर पूर्णांकन करना निर्दिष्ट गुणज में पूर्णांकन करने से बहुत भिन्न होता है; उदाहरण के लिए, किसी संख्या को 2 की पूर्ण शक्ति तक सन्निकट करने की आवश्यकता की गणना करने में यह सामान्य है। सामान्य रूप से, एक धनात्मक संख्या को पूर्णांक बनाने के चरण x कुछ सकारात्मक संख्या की शक्ति के लिए b 1 के अलावा, हैं:

\mathrm {roundToPower} (x,b)=b^{\mathrm {round} (\log _{b}x)},x>0,b>0,b\neq 1

गुणज में पूर्णांकन करने के लिए लागू कई चेतावनियाँ किसी घात के पूर्णांकन पर लागू होती हैं।

स्केल्ड राउंडिंग

इस प्रकार की गोलाई, जिसे लघुगणकीय पैमाने पर गोल करने का नाम भी दिया जाता है, एक निर्दिष्ट शक्ति के लिए #Rounding का एक प्रकार है। लॉगरिदमिक स्केल पर राउंडिंग राशि का लॉग लेकर और लॉग स्केल पर निकटतम मान पर सामान्य राउंडिंग करके पूरा किया जाता है।

उदाहरण के लिए, प्रतिरोधों को लघुगणकीय पैमाने पर पसंदीदा संख्याओं के साथ आपूर्ति की जाती है। विशेष रूप से, 10% सटीकता वाले प्रतिरोधों के लिए, उन्हें नाममात्र मान 100, 120, 150, 180, 220, आदि के साथ 10 (E12 श्रृंखला) के गुणकों में दिया जाता है। यदि एक गणना इंगित करती है कि 165 ओम के प्रतिरोधक की आवश्यकता है तो log(150)=2.176, log(165)=2.217 और log(180)=2.255। 165 का लघुगणक 180 के लघुगणक के करीब है इसलिए कोई अन्य विचार नहीं होने पर 180 ओम अवरोधक पहली पसंद होगा।

चाहे मान हो $x \in (a, b)$ राउंड टू a या b चुकता मान पर निर्भर करता है $x 2$ उत्पाद से अधिक या कम है $ab$ . प्रतिरोधों के उदाहरण में मान 165 राउंड से 180 तक है क्योंकि $1652 = 27225$ से बड़ा है $150 \times 180 = 27000$ .

फ़्लोटिंग-पॉइंट राउंडिंग

फ़्लोटिंग-पॉइंट अंकगणित में, राउंडिंग का उद्देश्य किसी दिए गए मान को चालू करना है x एक मूल्य में y की निर्दिष्ट संख्या के साथ significant अंक। दूसरे शब्दों में, y किसी संख्या का गुणज होना चाहिए m के परिमाण पर निर्भर करता है x. जो नंबर m फ़्लोटिंग-पॉइंट प्रतिनिधित्व के रेडिक्स (आमतौर पर 2 या 10) की शक्ति है।

इस विवरण के अलावा, ऊपर बताए गए राउंडिंग के सभी वेरिएंट फ्लोटिंग-पॉइंट नंबरों की राउंडिंग पर भी लागू होते हैं। इस तरह के राउंडिंग के लिए एल्गोरिथ्म ऊपर #Scaled राउंडिंग सेक्शन में प्रस्तुत किया गया है, लेकिन एक निरंतर स्केलिंग फैक्टर के साथ s = 1, और एक पूर्णांक आधार b > 1.

जहां राउंडेड परिणाम एक निर्देशित राउंडिंग के परिणाम को ओवरफ्लो कर देगा, या तो शून्य से दूर राउंडिंग करते समय उपयुक्त हस्ताक्षरित अनंत है, या उच्चतम प्रतिनिधित्व योग्य सकारात्मक परिमित संख्या (या सबसे कम प्रतिनिधित्व योग्य नकारात्मक परिमित संख्या यदि x ऋणात्मक है), जब शून्य की ओर गोल होता है। राउंड टू नियरेस्ट के सामान्य मामले के लिए अतिप्रवाह का परिणाम हमेशा उपयुक्त अनंत होता है।

एक साधारण अंश के लिए गोलाई

कुछ संदर्भों में किसी दी गई संख्या को गोल करना वांछनीय है x एक साफ अंश के लिए — यानी, निकटतम भिन्न y = m/n जिसका अंश m और भाजक n दिए गए अधिकतम से अधिक न हो। यह समस्या किसी मान को दशमलव या बाइनरी अंकों की एक निश्चित संख्या में, या किसी दी गई इकाई के गुणक में गोल करने से काफी अलग है m. यह समस्या फेरी अनुक्रमों, स्टर्न-ब्रोकॉट ट्री और निरंतर अंशों से संबंधित है।

उपलब्ध मान पर पूर्णांक बनाना

तैयार लकड़ी, लेखन पत्र, कैपेसिटर और कई अन्य उत्पाद आमतौर पर केवल कुछ मानक आकारों में बेचे जाते हैं।

कई डिज़ाइन प्रक्रियाएं वर्णन करती हैं कि अनुमानित मूल्य की गणना कैसे करें, और फिर वाक्यांशों का उपयोग करके कुछ मानक आकार के लिए गोल करें जैसे निकटतम मानक मान तक गोल करें, निकटतम मानक मान तक गोल करें, या निकटतम मानक मान पर गोल करें।^[9]^[10] जब पसंदीदा मानों का एक सेट लॉगरिदमिक पैमाने पर समान रूप से स्थान दिया जाता है, तो किसी भी दिए गए मान के निकटतम पसंदीदा मान को चुनना #स्केल राउंडिंग के रूप में देखा जा सकता है। ऐसे गोल मूल्यों की सीधे गणना की जा सकती है।^[11]

अन्य संदर्भों में पूर्णांकन

डिथरिंग और त्रुटि प्रसार

ध्वनि तरंगों जैसे निरंतर संकेतों को डिजिटाइज़ करते समय, प्रत्येक माप की सटीकता की तुलना में कई मापों का समग्र प्रभाव अधिक महत्वपूर्ण होता है। इन परिस्थितियों में, डिथरिंग और एक संबंधित तकनीक, त्रुटि प्रसार, का सामान्य रूप से उपयोग किया जाता है। पल्स-चौड़ाई मॉडुलन नामक एक संबंधित तकनीक का उपयोग चर कर्तव्य चक्र के साथ शक्ति को तेजी से स्पंदित करके एक जड़त्वीय उपकरण से एनालॉग प्रकार के आउटपुट को प्राप्त करने के लिए किया जाता है।

त्रुटि प्रसार त्रुटि को सुनिश्चित करने की कोशिश करता है, औसतन, कम से कम है। एक से शून्य तक एक कोमल ढलान के साथ काम करते समय, पहले कुछ शब्दों के लिए आउटपुट शून्य होगा जब तक कि त्रुटि का योग और वर्तमान मान 0.5 से अधिक नहीं हो जाता है, इस मामले में 1 आउटपुट होता है और अंतर को त्रुटि से घटाया जाता है। अब तक। फ्लोयड-स्टाइनबर्ग डिथरिंग छवियों को डिजिटाइज़ करते समय एक लोकप्रिय त्रुटि प्रसार प्रक्रिया है।

एक आयामी उदाहरण के रूप में, संख्याओं को मान लीजिए 0.9677, 0.9204, 0.7451, और 0.3091 क्रम में होता है और प्रत्येक को एक से अधिक में गोल किया जाना है 0.01. इस मामले में संचयी रकम, 0.9677, 1.8881 = 0.9677 + 0.9204, 2.6332 = 0.9677 + 0.9204 + 0.7451, और 2.9423 = 0.9677 + 0.9204 + 0.7451 + 0.3091, प्रत्येक को के गुणज में पूर्णांकित किया जाता है 0.01: 0.97, 1.89, 2.63, और 2.94. इनमें से पहला और आसन्न मूल्यों के अंतर वांछित गोल मान देते हैं: 0.97, 0.92 = 1.89 − 0.97, 0.74 = 2.63 − 1.89, और 0.31 = 2.94 − 2.63.

मोंटे कार्लो अंकगणित

मोंटे कार्लो अंकगणित मोंटे कार्लो विधियों में एक तकनीक है जहां गोलाई बेतरतीब ढंग से ऊपर या नीचे होती है। मोंटे कार्लो अंकगणित के लिए स्टोचैस्टिक राउंडिंग का उपयोग किया जा सकता है, लेकिन सामान्य तौर पर, समान संभावना के साथ बस ऊपर या नीचे गोल करना अधिक बार उपयोग किया जाता है। बार-बार चलने से परिणामों का एक यादृच्छिक वितरण होगा जो गणना की स्थिरता का संकेत दे सकता है।^[12]

=== गोलाकार अंकगणित === के साथ सटीक गणना पूर्णांक डोमेन और श्रेणी वाले फ़ंक्शन के सटीक मान का मूल्यांकन करने के लिए गोलाकार अंकगणितीय का उपयोग करना संभव है। उदाहरण के लिए, यदि एक पूर्णांक n को एक पूर्ण वर्ग के रूप में जाना जाता है, इसके वर्गमूल की गणना परिवर्तित करके की जा सकती है n फ़्लोटिंग-पॉइंट मान पर z, अनुमानित वर्गमूल की गणना करना x का z फ्लोटिंग पॉइंट के साथ, और फिर राउंडिंग x निकटतम पूर्णांक तक y. अगर n बहुत बड़ा नहीं है, फ़्लोटिंग-पॉइंट राउंड-ऑफ त्रुटि x 0.5 से कम होगा, इसलिए गोल मान y का सटीक वर्गमूल होगा n. यही कारण है कि सटीक अंकगणित के लिए स्लाइड नियमों का उपयोग किया जा सकता है।

डबल राउंडिंग

सटीकता के विभिन्न स्तरों के क्रम में किसी संख्या को दो बार राउंड करना, बाद की सटीकता मोटे होने के साथ, निर्देशित राउंडिंग के मामले को छोड़कर अंतिम सटीकता के लिए एक बार राउंडिंग के समान परिणाम देने की गारंटी नहीं है।^{[nb 1]}उदाहरण के लिए 9.46 को एक दशमलव तक राउंड करने पर 9.5 मिलता है, और फिर 10 को राउंडिंग हाफ का उपयोग करके पूर्णांक तक राउंडिंग करते समय 10 देता है, लेकिन सीधे पूर्णांक में राउंड करने पर 9 देता है। बोरमैन और चैटफील्ड^[13] पूर्णांकों का उपयोग करके व्यक्त की गई विनिर्देश सीमाओं के लिए एक दशमलव स्थान पर राउंडेड डेटा की तुलना करते समय डबल राउंडिंग के निहितार्थों पर चर्चा करें।

1995 और 1997 के बीच मार्टिनेज बनाम ऑलस्टेट और सेंडेजो बनाम किसान मुकदमेबाजी में, बीमा कंपनियों ने तर्क दिया कि प्रीमियम को दोगुना करने की अनुमति थी और वास्तव में इसकी आवश्यकता थी। अमेरिकी अदालतों ने बीमा कंपनियों के खिलाफ फैसला सुनाया और उन्हें सिंगल राउंडिंग सुनिश्चित करने के लिए नियम अपनाने का आदेश दिया।^[14] कुछ कंप्यूटर भाषाएँ और IEEE 754-2008 संशोधन|IEEE 754-2008 मानक निर्धारित करते हैं कि सीधी गणनाओं में परिणाम को दो बार गोल नहीं किया जाना चाहिए। यह जावा के साथ एक विशेष समस्या रही है क्योंकि इसे अलग-अलग मशीनों पर समान रूप से चलाने के लिए डिज़ाइन किया गया है, x87 फ़्लोटिंग पॉइंट के साथ इसे प्राप्त करने के लिए विशेष प्रोग्रामिंग ट्रिक्स का उपयोग किया जाना है।^[15]^[16] जावा भाषा को अलग-अलग परिणामों की अनुमति देने के लिए बदल दिया गया था जहां अंतर मायने नहीं रखता था और जब परिणामों को सटीक रूप से अनुरूप बनाना होता है तो सख्त एफपी क्वालीफायर का उपयोग करने की आवश्यकता होती है; जावा 17 में सख्त फ़्लोटिंग पॉइंट को पुनर्स्थापित कर दिया गया है।^[17] कुछ एल्गोरिदम में, एक मध्यवर्ती परिणाम की गणना एक बड़ी सटीकता में की जाती है, फिर इसे अंतिम सटीकता के लिए गोल किया जाना चाहिए। मध्यवर्ती संगणना के लिए पर्याप्त पूर्णांकन चुनकर दोहरी गोलाई से बचा जा सकता है। इसमें अंतिम राउंडिंग के लिए मिडपॉइंट पर राउंड करने से बचना शामिल है (सिवाय इसके कि जब मिडपॉइंट सटीक हो)। बाइनरी अंकगणित में, परिणाम को शून्य की ओर गोल करने का विचार है, और यदि गोल परिणाम गलत है तो कम से कम महत्वपूर्ण बिट को 1 पर सेट करें; इस गोलाई को स्टिकी गोलाई कहा जाता है।^[18] समतुल्य रूप से, यह मध्यवर्ती परिणाम को वापस करने में शामिल होता है जब यह बिल्कुल प्रतिनिधित्व योग्य होता है, और एक विषम महत्व के साथ निकटतम फ़्लोटिंग-पॉइंट संख्या और अन्यथा; यही कारण है कि इसे राउंडिंग टू ऑड भी कहा जाता है।^[19]^[20] बाइनरी और दशमलव अंकगणित के लिए इस दृष्टिकोण का एक ठोस कार्यान्वयन, छोटी सटीकता के लिए तैयार करने के लिए #Rounding के रूप में लागू किया गया है।

टेबल-मेकर की दुविधा

विलियम एम. कहन ने पारलौकिक कार्यों को पूरा करने की अज्ञात लागत के लिए द टेबल-मेकर्स डिलेमा शब्द गढ़ा:

Nobody knows how much it would cost to compute y^w correctly rounded for every two floating-point arguments at which it does not over/underflow. Instead, reputable math libraries compute elementary transcendental functions mostly within slightly more than half an ulp and almost always well within one ulp. Why can't y^w be rounded within half an ulp like SQRT? Because nobody knows how much computation it would cost... No general way exists to predict how many extra digits will have to be carried to compute a transcendental expression and round it correctly to some preassigned number of digits. Even the fact (if true) that a finite number of extra digits will ultimately suffice may be a deep theorem.^[21]

IEEE 754 फ़्लोटिंग-प्वाइंट मानक गारंटी देता है कि जोड़, घटाव, गुणा, भाग, फ़्यूज्ड गुणा-जोड़, वर्गमूल और फ़्लोटिंग-पॉइंट शेष अनंत-परिशुद्धता ऑपरेशन का सही ढंग से गोल परिणाम देगा। अधिक जटिल कार्यों के लिए 1985 के मानक में ऐसी कोई गारंटी नहीं दी गई थी और वे आम तौर पर केवल अंतिम बिट के भीतर ही सटीक होते हैं। हालांकि, 2008 मानक गारंटी देता है कि अनुरूप कार्यान्वयन सही ढंग से गोल परिणाम देगा जो सक्रिय राउंडिंग मोड का सम्मान करते हैं; हालाँकि, कार्यों का कार्यान्वयन वैकल्पिक है।

गेल्फ़ोंड-श्नाइडर प्रमेय और लिंडमैन-वीयरस्ट्रास प्रमेय का उपयोग करके, कुछ प्रसिद्ध तर्कों को छोड़कर, मानक प्राथमिक कार्यों में से कई को पारलौकिक संख्या परिणाम वापस करने के लिए सिद्ध किया जा सकता है; इसलिए, सैद्धांतिक दृष्टिकोण से, ऐसे कार्यों को सही ढंग से गोल करना हमेशा संभव होता है। हालांकि, इस तरह के एक समारोह के कार्यान्वयन के लिए, सटीक परिणामों की गणना करने की आवश्यकता के बारे में एक निश्चित सटीकता के लिए एक सीमा निर्धारित करने से पहले, एक सही ढंग से गोल परिणाम की गारंटी दी जा सकती है, बहुत अधिक गणना समय की मांग कर सकते हैं या पहुंच से बाहर हो सकते हैं।^[22] व्यवहार में, जब यह सीमा ज्ञात नहीं है (या केवल एक बहुत बड़ी सीमा ज्ञात है), कार्यान्वयन में कुछ निर्णय लिया जाना है (नीचे देखें); लेकिन एक संभाव्य मॉडल के अनुसार, लक्ष्य प्रारूप के अंकों की संख्या के दोगुने तक की मध्यवर्ती सटीकता और कुछ छोटे स्थिरांक (विशेष मामलों को ध्यान में रखने के बाद) का उपयोग करते समय सही गोलाई को बहुत अधिक संभावना से संतुष्ट किया जा सकता है।

कुछ प्रोग्रामिंग पैकेज सही गोलाई प्रदान करते हैं। जीएनयू एमपीएफआर पैकेज सही ढंग से गोलाकार मनमाना सटीक परिणाम देता है। कुछ अन्य पुस्तकालय दोहरी परिशुद्धता में सही गोलाई के साथ प्राथमिक कार्यों को लागू करते हैं:

IBM का ml4j, जो 1999 में अब्राहम ज़िव और मोशे ओलशनस्की द्वारा लिखित जावा के लिए गणितीय पुस्तकालय के लिए खड़ा है, सही ढंग से केवल निकटतम तक गोल है। रेफरी>"एनए डाइजेस्ट संडे, अप्रैल 18, 1999 वॉल्यूम 99 : अंक 16". 1999-04-18. Retrieved 2022-08-29.</ref>^[23] इस पुस्तकालय के पोर्टेबल होने का दावा किया गया था, लेकिन केवल PowerPC/IBM AIX, SPARC/Oracle Solaris और x86/Windows NT के लिए बायनेरिज़ प्रदान किए गए थे। इसके प्रलेखन के अनुसार, यह लाइब्रेरी पहले चरण का उपयोग सटीकता के साथ दोगुनी सटीकता से थोड़ी बड़ी है, दूसरा चरण डबल-डबल अंकगणित पर आधारित है, और आईईईई 754 डबल-परिशुद्धता के सरणियों के आधार पर 768-बिट परिशुद्धता के साथ तीसरा चरण है। दशमलव संख्याएं।
आईबीएम की सटीक पोर्टेबल गणितीय लाइब्रेरी (एपीमैथलिब या सिर्फ मैथलिब के रूप में संक्षिप्त),^[24]^[25] लिबुल्टिम भी कहा जाता है,^[26] केवल निकटतम तक गोलाई में। यह लाइब्रेरी 768 बिट्स तक कार्य करने की सटीकता का उपयोग करती है। इसे 2001 में GNU C लाइब्रेरी में शामिल किया गया था,^[27] लेकिन 2018 से 2021 तक धीमे रास्तों (सही गोलाई प्रदान करने वाले) को हटा दिया गया।
सन माइक्रोसिस्टम्स का libmcr, 4 राउंडिंग मोड में।^[28] कठिन मामलों के लिए, यह पुस्तकालय कई सटीकता का भी उपयोग करता है, और हर बार टेबल-मेकर की दुविधा होने पर शब्दों की संख्या 2 से बढ़ जाती है (मशीन की कुछ सीमा तक पहुंचने की बहुत ही असंभव घटना में अपरिभाषित व्यवहार के साथ)।
CRlibm, पुरानी Arénaire टीम (LIP, ENS Lyon) में लिखा गया है। यह 4 राउंडिंग मोड का समर्थन करता है और सबसे कठिन-टू-राउंड मामलों के ज्ञान का उपयोग करके सिद्ध होता है।^[29]^[30]
कोर-मैथ प्रोजेक्ट 4 राउंडिंग मोड में कुछ सही ढंग से राउंडेड फ़ंक्शन प्रदान करता है, सबसे कठिन-टू-राउंड मामलों के ज्ञान का उपयोग करके।^[31]^[32]

ऐसी संगणनीय संख्याएँ मौजूद हैं जिनके लिए एक गोल मान कभी भी निर्धारित नहीं किया जा सकता है चाहे कितने ही अंकों की गणना की जाए। विशिष्ट उदाहरण नहीं दिए जा सकते हैं, लेकिन यह हॉल्टिंग समस्या की अनिश्चयता के कारण होता है। उदाहरण के लिए, यदि गोल्डबैक का अनुमान सही है लेकिन सिद्ध नहीं किया जा सकता है, तो निम्न मान को राउंड अप करने का परिणाम #राउंडिंग अप निर्धारित नहीं किया जा सकता है: या तो 1+10⁻ⁿ कहाँ n 4 से बड़ी पहली सम संख्या है जो दो अभाज्य संख्याओं का योग नहीं है, या 1 यदि ऐसी कोई संख्या नहीं है। ऐसी संख्या होने पर गोल परिणाम 2 होता है n मौजूद है और 1 अन्यथा। राउंडिंग से पहले के मान को किसी भी सटीक सटीकता के साथ अनुमानित किया जा सकता है, भले ही अनुमान अप्राप्य हो।

स्ट्रिंग खोजों के साथ सहभागिता

राउंडिंग किसी संख्या के लिए स्ट्रिंग खोज पर प्रतिकूल प्रभाव डाल सकती है। उदाहरण के लिए, $π$ को चार अंकों में बदलना 3.1416 है लेकिन इस स्ट्रिंग के लिए एक साधारण खोज 3.14159 या किसी अन्य मूल्य की खोज नहीं करेगी $π$ को चार से अधिक अंकों में गोल किया गया। इसके विपरीत, ट्रंकेशन इस समस्या से पीड़ित नहीं होता है; उदाहरण के लिए, 3.1415 के लिए एक साधारण स्ट्रिंग खोज, जो है $π$ को चार अंकों तक छोटा किया गया है, के मानों की खोज करेगा $π$ चार से अधिक अंकों तक छोटा किया गया।

इतिहास

गोलाई की अवधारणा बहुत पुरानी है, शायद विभाजन की अवधारणा से भी पुरानी है। मेसोपोटामिया में पाई जाने वाली कुछ प्राचीन मिट्टी की गोलियों में बेस 60 में गुणक व्युत्क्रम और वर्गमूल के गोल मान वाली तालिकाएँ होती हैं।^[33] पाई के लिए गोल सन्निकटन $π$ , वर्ष की लंबाई, और महीने की लंबाई भी प्राचीन हैं—सेक्सेजिमल#उदाहरण देखें।

राउंड-टू-ईवन विधि ने 1940 से ASTM (E-29) मानक के रूप में कार्य किया है। निष्पक्ष राउंडिंग और स्टेटिस्टिशियन्स राउंडिंग शब्दों की उत्पत्ति काफी आत्म-व्याख्यात्मक है। 1906 में प्रोबेबिलिटी एंड थ्योरी ऑफ एरर्स का चौथा संस्करण^[34] रॉबर्ट सिम्पसन वुडवर्ड ने इसे कंप्यूटर का नियम कहा जो दर्शाता है कि यह तब मानव कंप्यूटरों द्वारा सामान्य उपयोग में था जो गणितीय तालिकाओं की गणना करते थे। चर्चिल आइजनहार्ट ने संकेत दिया कि यह अभ्यास 1940 के दशक तक डेटा विश्लेषण में अच्छी तरह से स्थापित हो चुका था।^[35] बैंकर्स राउंडिंग शब्द की उत्पत्ति अधिक अस्पष्ट बनी हुई है। यदि यह राउंडिंग विधि कभी बैंकिंग में एक मानक थी, तो साक्ष्य खोजना अत्यंत कठिन साबित हुआ है। इसके विपरीत, यूरोपीय आयोग की धारा 2 रिपोर्ट यूरो का परिचय और मुद्रा राशियों का पूर्णांकन^[36] सुझाव देता है कि पहले बैंकिंग में राउंडिंग के लिए कोई मानक दृष्टिकोण नहीं था; और यह निर्दिष्ट करता है कि आधी-अधूरी मात्रा को राउंड अप किया जाना चाहिए।

1980 के दशक तक, फ्लोटिंग-पॉइंट कंप्यूटर अंकगणित में उपयोग की जाने वाली राउंडिंग विधि आमतौर पर हार्डवेयर द्वारा तय की जाती थी, खराब प्रलेखित, असंगत और प्रत्येक ब्रांड और कंप्यूटर के मॉडल के लिए अलग होती थी। अधिकांश कंप्यूटर निर्माताओं द्वारा IEEE 754 फ़्लोटिंग-पॉइंट मानक को अपनाने के बाद यह स्थिति बदल गई। मानक उपयोगकर्ता को कई राउंडिंग मोड्स में से चुनने की अनुमति देता है, और प्रत्येक मामले में सटीक रूप से निर्दिष्ट करता है कि परिणाम कैसे राउंड किए जाने चाहिए। इन विशेषताओं ने संख्यात्मक संगणनाओं को अधिक अनुमानित और मशीन-स्वतंत्र बना दिया, और अंतराल अंकगणित के कुशल और सुसंगत कार्यान्वयन को संभव बनाया।

वर्तमान में, बहुत से शोध 5 या 2 के गुणकों में गोल हो जाते हैं। उदाहरण के लिए, जॉर्ग बैटन ने प्राचीन आबादी के संख्यात्मक स्तर का मूल्यांकन करने के लिए कई अध्ययनों में उम्र के ढेर का इस्तेमाल किया। वह व्हिपल के इंडेक्स#एबीसीसी इंडेक्स के साथ आया, जो किसी भी ऐतिहासिक स्रोत के बिना संभावित क्षेत्रों के बीच संख्यात्मकता की तुलना करने में सक्षम बनाता है जहां जनसंख्या साक्षरता को मापा गया था।^[37]

प्रोग्रामिंग भाषाओं में राउंडिंग फ़ंक्शंस

अधिकांश प्रोग्रामिंग भाषाएं भिन्नात्मक संख्याओं को विभिन्न तरीकों से गोल करने के लिए फ़ंक्शन या विशेष सिंटैक्स प्रदान करती हैं। शुरुआती अंकीय भाषाएं, जैसे फोरट्रान और सी (प्रोग्रामिंग भाषा), केवल एक विधि प्रदान करती हैं, आमतौर पर ट्रंकेशन (शून्य की ओर)। यह डिफ़ॉल्ट विधि कुछ संदर्भों में निहित हो सकती है, जैसे कि एक पूर्णांक (कंप्यूटर विज्ञान) चर (प्रोग्रामिंग) के लिए एक भिन्नात्मक संख्या निर्दिष्ट करते समय, या किसी सरणी डेटा प्रकार के सूचकांक के रूप में एक भिन्नात्मक संख्या का उपयोग करना। अन्य प्रकार की गोलाई को स्पष्ट रूप से प्रोग्राम किया जाना था; उदाहरण के लिए, किसी धनात्मक संख्या को निकटतम पूर्णांक तक पूर्णांक बनाना 0.5 जोड़कर और काट-छाँट करके लागू किया जा सकता है।

हालांकि, पिछले दशकों में, अधिकांश भाषाओं के सिंटैक्स और मानक पुस्तकालय (कंप्यूटिंग) ने आमतौर पर कम से कम चार बुनियादी राउंडिंग फ़ंक्शन (ऊपर, नीचे, निकटतम और शून्य की ओर) प्रदान किए हैं। टाई-ब्रेकिंग विधि भाषा और संस्करण के आधार पर भिन्न हो सकती है या प्रोग्रामर द्वारा चयन योग्य हो सकती है। कई भाषाएँ IEEE 754 फ़्लोटिंग-पॉइंट मानक का पालन करती हैं, और इन कार्यों को एक डबल-परिशुद्धता फ़्लोटिंग-पॉइंट प्रारूप | डबल-परिशुद्धता फ़्लोट तर्क लेने और उसी प्रकार के परिणाम को वापस करने के रूप में परिभाषित करती हैं, जिसे तब परिवर्तित किया जा सकता है। यदि आवश्यक हो तो पूर्णांक। यह दृष्टिकोण नकली पूर्णांक अतिप्रवाह से बच सकता है क्योंकि फ़्लोटिंग-पॉइंट प्रकारों में पूर्णांक प्रकारों की तुलना में बड़ी सीमा होती है। कुछ भाषाएँ, जैसे कि PHP, ऐसे कार्य प्रदान करती हैं जो किसी मान को दशमलव अंकों की निर्दिष्ट संख्या तक ले जाते हैं (उदाहरण के लिए, 4321.5678 से 4321.57 या 4300 तक)। इसके अलावा, कई भाषाएँ एक printf ़ या समान स्ट्रिंग स्वरूपण फ़ंक्शन प्रदान करती हैं, जो एक भिन्नात्मक संख्या को एक स्ट्रिंग में बदलने की अनुमति देती है, जो उपयोगकर्ता द्वारा निर्दिष्ट दशमलव स्थानों की संख्या (परिशुद्धता) के लिए गोल होती है। दूसरी ओर, ट्रंकेशन (राउंड टू जीरो) अभी भी कई भाषाओं द्वारा उपयोग की जाने वाली डिफ़ॉल्ट राउंडिंग विधि है, विशेष रूप से दो पूर्णांक मानों के विभाजन के लिए।

इसके विपरीत, व्यापक शैली पत्रक और स्केलेबल वेक्टर ग्राफिक्स संख्याओं और मापों के लिए किसी विशिष्ट अधिकतम सटीकता को परिभाषित नहीं करते हैं, जिसे वे अपने दस्तावेज़ ऑब्जेक्ट मॉडल में और उनके इंटरफ़ेस विवरण भाषा इंटरफ़ेस में स्ट्रिंग्स के रूप में मानते हैं और प्रकट करते हैं जैसे कि उनके पास वास्तविक रैम है, और करते हैं पूर्णांक और फ़्लोटिंग-पॉइंट मानों के बीच भेदभाव नहीं; हालांकि, इन भाषाओं का कार्यान्वयन सीमित सटीकता के साथ गणना किए गए अंकों को उजागर करने से पहले इन संख्याओं को आम तौर पर IEEE 754 डबल-परिशुद्धता फ़्लोटिंग-पॉइंट मानों में परिवर्तित कर देगा (विशेष रूप से मानक जावास्क्रिप्ट या ECMAScript के भीतर)^[38] इंटरफ़ेस बाइंडिंग)।

अन्य राउंडिंग मानक

कुछ विषयों या संस्थानों ने पूर्णांकन के लिए मानक या निर्देश जारी किए हैं।

अमेरिकी मौसम अवलोकन

1966 के मध्य में जारी एक दिशानिर्देश में,^[39] युनाइटेड स्टेट्स|यू.एस. मौसम विज्ञान के लिए संघीय समन्वयक के कार्यालय ने निर्धारित किया है कि मौसम डेटा को निकटतम गोल संख्या में राउंड हाफ अप टाई-ब्रेकिंग नियम के साथ राउंड किया जाना चाहिए। उदाहरण के लिए, 1.5 को पूर्णांक बनाने के लिए 2 होना चाहिए, और −1.5 को −1 होना चाहिए। उस तिथि से पहले, टाई-ब्रेकिंग नियम शून्य से लगभग आधा दूर था।

मौसम विज्ञान में नकारात्मक शून्य

कुछ मौसम विज्ञानी -0 को 0.0 और -0.5 डिग्री (अनन्य) के बीच के तापमान को इंगित करने के लिए लिख सकते हैं जो एक पूर्णांक के लिए गोल था। इस अंकन का उपयोग तब किया जाता है जब ऋणात्मक चिह्न को महत्वपूर्ण माना जाता है, चाहे परिमाण कितना भी छोटा क्यों न हो; उदाहरण के लिए, जब तापमान को सेल्सीयस पैमाने पर गोल किया जाता है, जहां शून्य से नीचे जमने का संकेत मिलता है।^{[citation needed]}

यह भी देखें

कैश राउंडिंग, बेहद कम मूल्य के सिक्कों की अनुपस्थिति से निपटना
डेटा बिनिंग, एक समान ऑपरेशन
गैल की सटीक टेबल
अंतराल अंकगणित
आईएसओ / आईईसी 80000
कहान योग एल्गोरिथम
पार्टी-सूची आनुपातिक प्रतिनिधित्व, पूर्णांकों को पूर्णांक बनाने का एक अनुप्रयोग जिसकी पूरी तरह से जांच की गई है
हस्ताक्षरित अंकों का प्रतिनिधित्व
छंटनी

संदर्भ

↑ Isaiah Lankham, Bruno Nachtergaele, Anne Schilling: Linear Algebra as an Introduction to Abstract Mathematics. World Scientific, Singapur 2016, ISBN 978-981-4730-35-8, p. 186.
↑ Kulisch, Ulrich W. (July 1977). "कंप्यूटर अंकगणित का गणितीय आधार". IEEE Transactions on Computers. C-26 (7): 610–621. doi:10.1109/TC.1977.1674893. S2CID 35883481.
↑ Higham, Nicholas John (2002). संख्यात्मक एल्गोरिदम की सटीकता और स्थिरता. p. 54. ISBN 978-0-89871-521-7.
↑ ^4.0 ^4.1 "java.math.RoundingMode". Oracle.
↑ ^5.0 ^5.1 "decimal — Decimal fixed point and floating point arithmetic". Python Software Foundation.
↑ Engineering Drafting Standards Manual (NASA), X-673-64-1F, p90
↑ IBM z/Architecture Principles of Operation
↑ ^8.0 ^8.1 Gupta, Suyog; Angrawl, Ankur; Gopalakrishnan, Kailash; Narayanan, Pritish (2016-02-09). "डीप लर्निंग लिमिटेड न्यूमेरिकल प्रिसिजन के साथ". p. 3. arXiv:1502.02551 [cs.LG].
↑ "जेनर डायोड वोल्टेज नियामक" (PDF). Archived (PDF) from the original on 2011-07-13. Retrieved 2010-11-24.
↑ "Build a Mirror Tester"
↑ Bruce Trump, Christine Schneider. "Excel Formula Calculates Standard 1%-Resistor Values". Electronic Design, 2002-01-21. [1]
↑ Parker, D. Stott; Eggert, Paul R.; Pierce, Brad (2000-03-28). "Monte Carlo Arithmetic: a framework for the statistical analysis of roundoff errors". IEEE Computation in Science and Engineering.
↑ Borman, Phil; Chatfield, Marion (2015-11-10). "गोल डेटा का उपयोग करने के खतरों से बचें". Journal of Pharmaceutical and Biomedical Analysis. 115: 506–507. doi:10.1016/j.jpba.2015.07.021. PMID 26299526.
↑ Deborah R. Hensler (2000). Class Action Dilemmas: Pursuing Public Goals for Private Gain. RAND. pp. 255–293. ISBN 0-8330-2601-1.
↑ Samuel A. Figueroa (July 1995). "When is double rounding innocuous?". ACM SIGNUM Newsletter. ACM. 30 (3): 21–25. doi:10.1145/221332.221334. S2CID 14829295.
↑ Roger Golliver (October 1998). "विस्तारित आईईईई हार्डवेयर का उपयोग करके डिफ़ॉल्ट ऑर्थोगोनल आईईईई डबल परिणाम कुशलता से तैयार करना" (PDF). Intel.
↑ Darcy, Joseph D. "JEP 306: Restore Always-Strict Floating-Point Semantics". Retrieved 2021-09-12.
↑ Moore, J. Strother; Lynch, Tom; Kaufmann, Matt (1996). "A mechanically checked proof of the correctness of the kernel of the AMD5K86 floating-point division algorithm" (PDF). IEEE Transactions on Computers. 47. CiteSeerX 10.1.1.43.3309. doi:10.1109/12.713311. Retrieved 2016-08-02.
↑ Boldo, Sylvie; Melquiond, Guillaume (2008). "Emulation of a FMA and correctly-rounded sums: proved algorithms using rounding to odd" (PDF). IEEE Transactions on Computers. 57 (4): 462–471. doi:10.1109/TC.2007.70819. S2CID 1850330. Retrieved 2016-08-02.
↑ "21718 – real.c rounding not perfect". gcc.gnu.org.
↑ Kahan, William Morton. "A Logarithm Too Clever by Half". Retrieved 2008-11-14.
↑ {{cite book |author-last1=Muller |author-first1=Jean-Michel |author-last2=Brisebarre |author-first2=Nicolas |author-last3=de Dinechin |author-first3=Florent |author-last4=Jeannerod |author-first4=Claude-Pierre |author-last5=Lefèvre |author-first5=Vincent |author-last6=Melquiond |author-first6=Guillaume |author-last7=Revol |author-first7=Nathalie |author7-link=Nathalie Revol |author-last8=Stehlé |author-first8=Damien |author-last9=Torres |author-first9=Serge |title=फ़्लोटिंग-प्वाइंट अंकगणित की पुस्तिका|date=2010 |publisher=Birkhäuser |edition=1 |isbn=978-0-8176-4704-9 |doi=10.1007/978-0-8176-4705-6 |lccn=2009939668|chapter=Chapter 12: Solving the Table Maker's Dilemma|chapter-url=http://cds.cern.ch/record/1315760}
↑ "जावा के लिए गणित पुस्तकालय". Archived from the original on 1999-05-08.
↑ "सटीक पोर्टेबल गणितीय पुस्तकालय". Archived from the original on 2005-02-07.
↑ mathlib on GitHub.
↑ "libultim – ultimate correctly-rounded elementary-function library". Archived from the original on 2021-03-01.
↑ "Git - glibc.git/commit". Sourceware.org. Retrieved 2022-07-18.
↑ "libmcr – correctly-rounded elementary-function library".
↑ "CRlibm – Correctly Rounded mathematical library". Archived from the original on 2016-10-27.
↑ crlibm on GitHub
↑ "कोर-मैथ प्रोजेक्ट". Retrieved 2022-08-30.
↑ Sibidanov, Alexei; Zimmermann, Paul; Glondu, Stéphane (2022). कोर-मैथ प्रोजेक्ट. 29th IEEE Symposium on Computer Arithmetic (ARITH 2022). Retrieved 2022-08-30.
↑ Duncan J. Melville. "YBC 7289 clay tablet". 2006
↑ त्रुटियों की संभावना और सिद्धांत. historical.library.cornell.edu. Mathematical monographs, no. 7. J. Wiley & Son. 1906.
↑ Churchill Eisenhart (1947). "Effects of Rounding or Grouping Data". In Eisenhart; Hastay; Wallis (eds.). वैज्ञानिक और औद्योगिक अनुसंधान, और उत्पादन और प्रबंधन इंजीनियरिंग के लिए सांख्यिकीय विश्लेषण की चयनित तकनीकें. New York: McGraw-Hill. pp. 187–223. Retrieved 2014-01-30.
↑ "यूरो का परिचय और मुद्रा राशियों का पूर्णांकन" (PDF). Archived (PDF) from the original on 2010-10-09. Retrieved 2011-08-19.
↑ Baten, Jörg (2009). "Quantifying Quantitative Literacy: Age Heaping and the History of Human Capital" (PDF). Journal of Economic History. 69 (3): 783–808. doi:10.1017/S0022050709001120. hdl:10230/481. S2CID 35494384.
↑ "ECMA-262 ECMAScript Language Specification" (PDF). ecma-international.org.
↑ OFCM, 2005: Federal Meteorological Handbook No. 1 Archived 1999-04-20 at the Wayback Machine, Washington, DC., 104 pp.

बाहरी संबंध

Weisstein, Eric W. "गोलाई". MathWorld.
An introduction to different rounding algorithms that is accessible to a general audience but especially useful to those studying computer science and electronics.
How To Implement Custom Rounding Procedures by Microsoft (broken)

[NB_Double-13] A case where double rounding always leads to the same value as directly rounding to the final precision is when the radix is odd.

[1] Isaiah Lankham, Bruno Nachtergaele, Anne Schilling: Linear Algebra as an Introduction to Abstract Mathematics. World Scientific, Singapur 2016, ISBN 978-981-4730-35-8, p. 186.

[2] Kulisch, Ulrich W. (July 1977). "कंप्यूटर अंकगणित का गणितीय आधार". IEEE Transactions on Computers. C-26 (7): 610–621. doi:10.1109/TC.1977.1674893. S2CID 35883481.

[3] Higham, Nicholas John (2002). संख्यात्मक एल्गोरिदम की सटीकता और स्थिरता. p. 54. ISBN 978-0-89871-521-7.

[java-4] 4.0 ^4.1 "java.math.RoundingMode". Oracle.

[python-5] 5.0 ^5.1 "decimal — Decimal fixed point and floating point arithmetic". Python Software Foundation.

[6] Engineering Drafting Standards Manual (NASA), X-673-64-1F, p90

[7] IBM z/Architecture Principles of Operation

[stochastic-8] 8.0 ^8.1 Gupta, Suyog; Angrawl, Ankur; Gopalakrishnan, Kailash; Narayanan, Pritish (2016-02-09). "डीप लर्निंग लिमिटेड न्यूमेरिकल प्रिसिजन के साथ". p. 3. arXiv:1502.02551 [cs.LG].

[9] "जेनर डायोड वोल्टेज नियामक" (PDF). Archived (PDF) from the original on 2011-07-13. Retrieved 2010-11-24.

[10] "Build a Mirror Tester"

[11] Bruce Trump, Christine Schneider. "Excel Formula Calculates Standard 1%-Resistor Values". Electronic Design, 2002-01-21. [1]

[12] Parker, D. Stott; Eggert, Paul R.; Pierce, Brad (2000-03-28). "Monte Carlo Arithmetic: a framework for the statistical analysis of roundoff errors". IEEE Computation in Science and Engineering.

[14] Borman, Phil; Chatfield, Marion (2015-11-10). "गोल डेटा का उपयोग करने के खतरों से बचें". Journal of Pharmaceutical and Biomedical Analysis. 115: 506–507. doi:10.1016/j.jpba.2015.07.021. PMID 26299526.

[15] Deborah R. Hensler (2000). Class Action Dilemmas: Pursuing Public Goals for Private Gain. RAND. pp. 255–293. ISBN 0-8330-2601-1.

[16] Samuel A. Figueroa (July 1995). "When is double rounding innocuous?". ACM SIGNUM Newsletter. ACM. 30 (3): 21–25. doi:10.1145/221332.221334. S2CID 14829295.

[17] Roger Golliver (October 1998). "विस्तारित आईईईई हार्डवेयर का उपयोग करके डिफ़ॉल्ट ऑर्थोगोनल आईईईई डबल परिणाम कुशलता से तैयार करना" (PDF). Intel.

[18] Darcy, Joseph D. "JEP 306: Restore Always-Strict Floating-Point Semantics". Retrieved 2021-09-12.

[19] Moore, J. Strother; Lynch, Tom; Kaufmann, Matt (1996). "A mechanically checked proof of the correctness of the kernel of the AMD5K86 floating-point division algorithm" (PDF). IEEE Transactions on Computers. 47. CiteSeerX 10.1.1.43.3309. doi:10.1109/12.713311. Retrieved 2016-08-02.

[20] Boldo, Sylvie; Melquiond, Guillaume (2008). "Emulation of a FMA and correctly-rounded sums: proved algorithms using rounding to odd" (PDF). IEEE Transactions on Computers. 57 (4): 462–471. doi:10.1109/TC.2007.70819. S2CID 1850330. Retrieved 2016-08-02.

[21] "21718 – real.c rounding not perfect". gcc.gnu.org.

[22] Kahan, William Morton. "A Logarithm Too Clever by Half". Retrieved 2008-11-14.

[Muller_2010-23] {{cite book |author-last1=Muller |author-first1=Jean-Michel |author-last2=Brisebarre |author-first2=Nicolas |author-last3=de Dinechin |author-first3=Florent |author-last4=Jeannerod |author-first4=Claude-Pierre |author-last5=Lefèvre |author-first5=Vincent |author-last6=Melquiond |author-first6=Guillaume |author-last7=Revol |author-first7=Nathalie |author7-link=Nathalie Revol |author-last8=Stehlé |author-first8=Damien |author-last9=Torres |author-first9=Serge |title=फ़्लोटिंग-प्वाइंट अंकगणित की पुस्तिका|date=2010 |publisher=Birkhäuser |edition=1 |isbn=978-0-8176-4704-9 |doi=10.1007/978-0-8176-4705-6 |lccn=2009939668|chapter=Chapter 12: Solving the Table Maker's Dilemma|chapter-url=http://cds.cern.ch/record/1315760}

[24] "जावा के लिए गणित पुस्तकालय". Archived from the original on 1999-05-08.

[25] "सटीक पोर्टेबल गणितीय पुस्तकालय". Archived from the original on 2005-02-07.

[26] thlib on GitHub.

[27] "libultim – ultimate correctly-rounded elementary-function library". Archived from the original on 2021-03-01.

[28] "Git - glibc.git/commit". Sourceware.org. Retrieved 2022-07-18.

[29] "libmcr – correctly-rounded elementary-function library".

[30] "CRlibm – Correctly Rounded mathematical library". Archived from the original on 2016-10-27.

[31] rlibm on GitHub

[32] "कोर-मैथ प्रोजेक्ट". Retrieved 2022-08-30.

[33] Sibidanov, Alexei; Zimmermann, Paul; Glondu, Stéphane (2022). कोर-मैथ प्रोजेक्ट. 29th IEEE Symposium on Computer Arithmetic (ARITH 2022). Retrieved 2022-08-30.

[34] Duncan J. Melville. "YBC 7289 clay tablet". 2006

[35] त्रुटियों की संभावना और सिद्धांत. historical.library.cornell.edu. Mathematical monographs, no. 7. J. Wiley & Son. 1906.

[36] Churchill Eisenhart (1947). "Effects of Rounding or Grouping Data". In Eisenhart; Hastay; Wallis (eds.). वैज्ञानिक और औद्योगिक अनुसंधान, और उत्पादन और प्रबंधन इंजीनियरिंग के लिए सांख्यिकीय विश्लेषण की चयनित तकनीकें. New York: McGraw-Hill. pp. 187–223. Retrieved 2014-01-30.

[37] "यूरो का परिचय और मुद्रा राशियों का पूर्णांकन" (PDF). Archived (PDF) from the original on 2010-10-09. Retrieved 2011-08-19.

[38] Baten, Jörg (2009). "Quantifying Quantitative Literacy: Age Heaping and the History of Human Capital" (PDF). Journal of Economic History. 69 (3): 783–808. doi:10.1017/S0022050709001120. hdl:10230/481. S2CID 35494384.

[39] "ECMA-262 ECMAScript Language Specification" (PDF). ecma-international.org.

[40] OFCM, 2005: Federal Meteorological Handbook No. 1 Archived 1999-04-20 at the Wayback Machine, Washington, DC., 104 pp.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[nb 1]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]