हेविसाइड स्टेप फ़ंक्शन

Heaviside step
The Heaviside step function, using the half-maximum convention
General information
सामान्य परिभाषा	$$H(x):={\begin{cases}1,&x>0\\0,&x<0\end{cases}}$$
आवेदन के क्षेत्र	Operational calculus

हेविसाइड स्टेप फ़ंक्शन, या यूनिट स्टेप फ़ंक्शन, आमतौर पर इसके द्वारा दर्शाया जाता है H या θ (लेकिन कभी कभी u, 1 या 𝟙), ओलिवर हेविसाइड के नाम पर एक समारोह की ओर कदम बढ़ाएं है, जिसका मान नकारात्मक तर्कों के लिए 0 (संख्या) और सकारात्मक तर्कों के लिए 1 (संख्या) है।Zhang, Weihong; Zhou, Ying (2021). "Level-set functions and parametric functions". संरचनात्मक अनुकूलन के लिए फ़ीचर-संचालित विधि. Elsevier. pp. 9–46. doi:10.1016/b978-0-12-821330-8.00002-x. हेविसाइड फ़ंक्शन, जिसे हेविसाइड स्टेप फ़ंक्शन भी कहा जाता है, एक असंतत फ़ंक्शन है। जैसा कि चित्र 2.13 में दिखाया गया है, यह नकारात्मक इनपुट के लिए शून्य और गैर-नकारात्मक इनपुट के लिए एक मान देता है।</ref> यह स्टेप फ़ंक्शंस के सामान्य वर्ग का एक उदाहरण है, जिनमें से सभी को इसके अनुवादों के रैखिक संयोजन के रूप में दर्शाया जा सकता है।

फ़ंक्शन को मूल रूप से अंतर समीकरणों के समाधान के लिए परिचालन कैलकुलस में विकसित किया गया था, जहां यह एक सिग्नल का प्रतिनिधित्व करता है जो एक निर्दिष्ट समय पर स्विच करता है और अनिश्चित काल तक स्विच ऑन रहता है। ओलिवर हेविसाइड, जिन्होंने टेलीग्राफिक संचार के विश्लेषण में एक उपकरण के रूप में परिचालन गणना विकसित किया, ने इस फ़ंक्शन का प्रतिनिधित्व किया 1.

हेविसाइड फ़ंक्शन को इस प्रकार परिभाषित किया जा सकता है:

• एक टुकड़ावार कार्य:
  $$H(x):={\begin{cases}1,&x\geq 0\\0,&x<0\end{cases}}$$
• इवरसन ब्रैकेट नोटेशन का उपयोग करना:
  $$H(x):=[x>0]$$
• एक सूचक कार्य:
  $$H(x):=\mathbf {1} _{x>0}=\mathbf {1} _{\mathbb {R} _{+}}(x)$$
• रैंप समारोह का व्युत्पन्न:
  $$H(x):={\frac {d}{dx}}\max\{x,0\}\quad {\mbox{for }}x\neq 0$$

डिराक डेल्टा फ़ंक्शन हेविसाइड फ़ंक्शन का व्युत्पन्न है

$$\delta (x)={\frac {d}{dx}}H(x)$$

इसलिए हेविसाइड फ़ंक्शन को डिराक डेल्टा फ़ंक्शन का अभिन्न अंग माना जा सकता है। इसे कभी-कभी इस प्रकार लिखा जाता है

$$H(x):=\int _{-\infty }^{x}\delta (s)\,ds$$

हालाँकि यह विस्तार उपयुक्त नहीं हो सकता है (या इसका कोई मतलब भी नहीं है)। x = 0, यह इस पर निर्भर करता है कि कोई किस औपचारिकता का उपयोग सम्मिलित अभिन्नों को अर्थ देने के लिए करता है δ. इस संदर्भ में, हेविसाइड फ़ंक्शन एक यादृच्छिक चर का संचयी वितरण फ़ंक्शन है जो लगभग निश्चित रूप से 0 है। (स्थिर यादृच्छिक चर देखें।)

परिचालन गणना में, उपयोगी उत्तर शायद ही कभी इस पर निर्भर करते हैं कि किस मूल्य का उपयोग किया जाता है H(0), तब से H का प्रयोग अधिकतर वितरण (गणित) के रूप में किया जाता है। हालाँकि, इस विकल्प के कार्यात्मक विश्लेषण और गेम सिद्धांत में कुछ महत्वपूर्ण परिणाम हो सकते हैं, जहाँ निरंतरता के अधिक सामान्य रूपों पर विचार किया जाता है। कुछ सामान्य विकल्प #शून्य तर्क देखे जा सकते हैं।

हेविसाइड स्टेप फ़ंक्शन के सन्निकटन का उपयोग जैव रसायन और तंत्रिका विज्ञान में किया जाता है, जहां स्टेप फ़ंक्शंस (जैसे कि हिल समीकरण (जैव रसायन) और माइकलिस-मेंटेन कैनेटीक्स | माइकलिस-मेंटेन समीकरण) के लॉजिस्टिक फ़ंक्शन सन्निकटन का उपयोग बाइनरी सेलुलर स्विच को अनुमानित करने के लिए किया जा सकता है। रासायनिक संकेतों के जवाब में.

विश्लेषणात्मक अनुमान

${\tfrac {1}{2}}+{\tfrac {1}{2}}\tanh(kx)={\frac {1}{1+e^{-2kx}}}$
स्टेप फ़ंक्शन तक इस प्रकार पहुंचता है k → ∞.

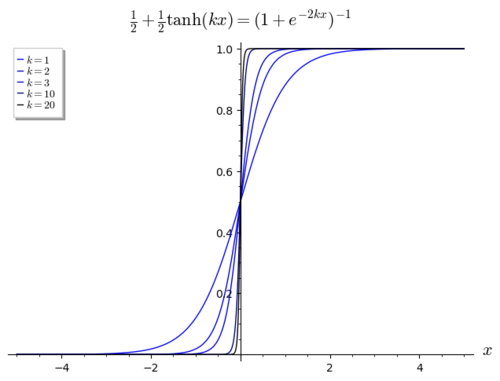
स्टेप फ़ंक्शन के सुचारू कार्य सन्निकटन के लिए, कोई लॉजिस्टिक फ़ंक्शन का उपयोग कर सकता है

$$H(x)\approx {\tfrac {1}{2}}+{\tfrac {1}{2}}\tanh kx={\frac {1}{1+e^{-2kx}}},$$

जहां एक बड़ा k एक तीव्र संक्रमण से मेल खाता है x = 0. अगर हम लेते हैं H(0) = 1/2, समानता सीमा में है:

$$H(x)=\lim _{k\to \infty }{\tfrac {1}{2}}(1+\tanh kx)=\lim _{k\to \infty }{\frac {1}{1+e^{-2kx}}}.$$

सिग्मॉइड फ़ंक्शन#उदाहरण|स्टेप फ़ंक्शन के कई अन्य सहज, विश्लेषणात्मक अनुमान हैं। संभावनाओं में से हैं:

$${\begin{aligned}H(x)&=\lim _{k\to \infty }\left({\tfrac {1}{2}}+{\tfrac {1}{\pi }}\arctan kx\right)\\H(x)&=\lim _{k\to \infty }\left({\tfrac {1}{2}}+{\tfrac {1}{2}}\operatorname {erf} kx\right)\end{aligned}}$$

ये सीमाएँ बिंदुवार और वितरण (गणित) के अर्थ में लागू होती हैं। हालाँकि, सामान्य तौर पर, बिंदुवार अभिसरण को वितरणात्मक अभिसरण की आवश्यकता नहीं होती है, और इसके विपरीत वितरणात्मक अभिसरण को बिंदुवार अभिसरण की आवश्यकता नहीं होती है। (हालाँकि, यदि कार्यों के बिंदुवार अभिसरण अनुक्रम के सभी सदस्य समान रूप से किसी अच्छे फ़ंक्शन से बंधे होते हैं, तो लेबेसेग अभिसरण प्रमेय पर हावी हो जाता है।)

सामान्य तौर पर, निरंतर वितरण संभाव्यता वितरण का कोई भी संचयी वितरण फ़ंक्शन जो शून्य के आसपास चरम पर होता है और इसमें एक पैरामीटर होता है जो विचरण के लिए नियंत्रण करता है, सीमा में एक अनुमान के रूप में काम कर सकता है क्योंकि विचरण शून्य के करीब पहुंचता है। उदाहरण के लिए, उपरोक्त तीनों सन्निकटन सामान्य संभाव्यता वितरण के संचयी वितरण कार्य हैं: क्रमशः लॉजिस्टिक वितरण, कॉची वितरण और सामान्य वितरण वितरण।

अभिन्न प्रतिनिधित्व

अक्सर हेविसाइड स्टेप फ़ंक्शन का एकीकरण (गणित) प्रतिनिधित्व उपयोगी होता है:

$${\begin{aligned}H(x)&=\lim _{\varepsilon \to 0^{+}}-{\frac {1}{2\pi i}}\int _{-\infty }^{\infty }{\frac {1}{\tau +i\varepsilon }}e^{-ix\tau }d\tau \\&=\lim _{\varepsilon \to 0^{+}}{\frac {1}{2\pi i}}\int _{-\infty }^{\infty }{\frac {1}{\tau -i\varepsilon }}e^{ix\tau }d\tau .\end{aligned}}$$

जहां दूसरा प्रतिनिधित्व पहले से निकालना आसान है, यह देखते हुए कि चरण फ़ंक्शन वास्तविक है और इस प्रकार इसका अपना जटिल संयुग्म है।

शून्य तर्क

तब से H आमतौर पर एकीकरण में उपयोग किया जाता है, और एक बिंदु पर किसी फ़ंक्शन का मान उसके अभिन्न अंग को प्रभावित नहीं करता है, यह शायद ही कभी मायने रखता है कि कौन सा विशेष मान चुना गया है H(0). सचमुच जब H को एक वितरण (गणित) या एक तत्व के रूप में माना जाता है L^∞ (एलपी स्पेस देखें|L^pस्पेस) शून्य पर मान की बात करने का भी कोई मतलब नहीं है, क्योंकि ऐसी वस्तुएं लगभग हर जगह ही परिभाषित की जाती हैं। यदि कुछ विश्लेषणात्मक सन्निकटन का उपयोग किया जाता है (जैसा कि #विश्लेषणात्मक सन्निकटन में है) तो अक्सर शून्य पर जो भी प्रासंगिक सीमा होती है उसका उपयोग किया जाता है।

किसी विशेष मान को चुनने के विभिन्न कारण मौजूद हैं।

• H(0) = 1/2 का उपयोग अक्सर किया जाता है क्योंकि किसी फ़ंक्शन के ग्राफ़ में घूर्णी समरूपता होती है; दूसरे तरीके से रखें, H − 1/2 तो एक अजीब कार्य है। इस मामले में साइन फ़ंक्शन के साथ निम्नलिखित संबंध सभी के लिए लागू होता है x:
  $$H(x)={\tfrac {1}{2}}(1+\operatorname {sgn} x).$$
• H(0) = 1 का प्रयोग कब किया जाता है H सही-निरंतर होने की आवश्यकता है। उदाहरण के लिए, संचयी वितरण कार्यों को आम तौर पर सही निरंतर माना जाता है, जैसे कि लेब्सग्यू-स्टिल्टजेस एकीकरण में कार्यों को एकीकृत किया जाता है। इस मामले में H एक बंद सेट अर्ध-अनंत अंतराल का सूचक कार्य है:
  $$H(x)=\mathbf {1} _{[0,\infty )}(x).$$
  संगत संभाव्यता वितरण विकृत वितरण है।
• H(0) = 0 का प्रयोग कब किया जाता है Hबाएं-निरंतर रहने की जरूरत है। इस मामले में H एक खुले सेट अर्ध-अनंत अंतराल का एक संकेतक कार्य है:
  $$H(x)=\mathbf {1} _{(0,\infty )}(x).$$
• अनुकूलन और गेम सिद्धांत से कार्यात्मक-विश्लेषण संदर्भों में, सीमित कार्यों की निरंतरता को संरक्षित करने और कुछ समाधानों के अस्तित्व को सुनिश्चित करने के लिए हेविसाइड फ़ंक्शन को बहुमूल्यांकित कार्य | सेट-वैल्यू फ़ंक्शन के रूप में परिभाषित करना अक्सर उपयोगी होता है। इन मामलों में, हेविसाइड फ़ंक्शन संभावित समाधानों का एक संपूर्ण अंतराल लौटाता है, H(0) = [0,1].

अलग रूप

इकाई चरण का एक वैकल्पिक रूप, जिसे एक फ़ंक्शन के रूप में परिभाषित किया गया है H : ℤ → ℝ (अर्थात, एक अलग चर लेना n), है:

$$H[n]={\begin{cases}0,&n<0,\\1,&n\geq 0,\end{cases}}$$

या आधे-अधिकतम सम्मेलन का उपयोग करना:

$$H[n]={\begin{cases}0,&n<0,\\{\tfrac {1}{2}},&n=0,\\1,&n>0,\end{cases}}$$

कहाँ n एक पूर्णांक है. अगर n तो फिर एक पूर्णांक है n < 0 इसका तात्पर्य यह होना चाहिए n ≤ −1, जबकि n > 0 इसका तात्पर्य यह होना चाहिए कि फ़ंक्शन एकता प्राप्त करता है n = 1. इसलिए स्टेप फ़ंक्शन के डोमेन पर रैंप जैसा व्यवहार प्रदर्शित करता है [−1, 1], और आधे-अधिकतम सम्मेलन का उपयोग करते हुए प्रामाणिक रूप से एक चरण फ़ंक्शन नहीं हो सकता है।

निरंतर मामले के विपरीत, की परिभाषा H[0]महत्वपूर्ण है.

असतत-समय इकाई आवेग, असतत-समय चरण का पहला अंतर है

$$\delta [n]=H[n]-H[n-1].$$

यह फ़ंक्शन क्रोनकर डेल्टा का संचयी योग है:

$$H[n]=\sum _{k=-\infty }^{n}\delta [k]$$

कहाँ

$$\delta [k]=\delta _{k,0}$$

पतित वितरण है.

प्रतिअवकलन और व्युत्पन्न

रैंप फ़ंक्शन हेविसाइड स्टेप फ़ंक्शन का एक प्रतिव्युत्पन्न है:

$$\int _{-\infty }^{x}H(\xi )\,d\xi =xH(x)=\max\{0,x\}\,.$$

हेविसाइड स्टेप फ़ंक्शन का वितरणात्मक व्युत्पन्न डिराक डेल्टा फ़ंक्शन है:

$${\frac {dH(x)}{dx}}=\delta (x)\,.$$

फूरियर रूपांतरण

हेविसाइड स्टेप फ़ंक्शन का फूरियर रूपांतरण एक वितरण है। हमारे पास फूरियर रूपांतरण की परिभाषा के लिए स्थिरांकों की एक पसंद का उपयोग करना है

$${\hat {H}}(s)=\lim _{N\to \infty }\int _{-N}^{N}e^{-2\pi ixs}H(x)\,dx={\frac {1}{2}}\left(\delta (s)-{\frac {i}{\pi }}\operatorname {p.v.} {\frac {1}{s}}\right).$$

यहाँ p.v.1/s वह वितरण (गणित) है जो एक परीक्षण कार्य करता है φ के कॉची प्रमुख मूल्य के लिए $\textstyle \int _{-\infty }^{\infty }{\frac {\varphi (s)}{s}}\,ds$. इंटीग्रल में दिखने वाली सीमा को (टेम्पर्ड) वितरण के अर्थ में भी लिया जाता है।

एकतरफ़ा लाप्लास परिवर्तन

हेविसाइड स्टेप फ़ंक्शन का लाप्लास ट्रांसफॉर्म एक मेरोमोर्फिक फ़ंक्शन है। एकतरफा लाप्लास परिवर्तन का उपयोग करते हुए हमारे पास:

$${\begin{aligned}{\hat {H}}(s)&=\lim _{N\to \infty }\int _{0}^{N}e^{-sx}H(x)\,dx\\&=\lim _{N\to \infty }\int _{0}^{N}e^{-sx}\,dx\\&={\frac {1}{s}}\end{aligned}}$$

जब द्विपक्षीय परिवर्तन का उपयोग किया जाता है, तो अभिन्न को दो भागों में विभाजित किया जा सकता है और परिणाम समान होगा।

अन्य भाव

हेविसाइड स्टेप फ़ंक्शन को हाइपरफ़ंक्शन के रूप में दर्शाया जा सकता है

$$H(x)=\left(1-{\frac {1}{2\pi i}}\log z,\ -{\frac {1}{2\pi i}}\log z\right).$$

कहाँ log z का जटिल लघुगणक#प्रधान मान है z.

इसके लिए भी व्यक्त किया जा सकता है x ≠ 0 निरपेक्ष मान फ़ंक्शन के संदर्भ में

$$H(x)={\frac {x+|x|}{2x}}\,.$$

यह भी देखें

• डिराक डेल्टा फ़ंक्शन
• सूचक कार्य
• इवरसन ब्रैकेट
• लाप्लास परिवर्तन
• सूचक का लाप्लासियन
• गणितीय कार्यों की सूची
• मैकाले कोष्ठक
• ऋणात्मक संख्या
• आयताकार कार्य
• साइन फ़ंक्शन
• साइन इंटीग्रल
• कदम की प्रतिक्रिया

बाहरी संबंध

• Digital Library of Mathematical Functions, NIST, [1].
• Berg, Ernst Julius (1936). "Unit function". Heaviside's Operational Calculus, as applied to Engineering and Physics. McGraw-Hill Education. p. 5.
• Calvert, James B. (2002). "Heaviside, Laplace, and the Inversion Integral". University of Denver.
• Davies, Brian (2002). "Heaviside step function". Integral Transforms and their Applications (3rd ed.). Springer. p. 28.
• Duff, George F. D.; Naylor, D. (1966). "Heaviside unit function". Differential Equations of Applied Mathematics. John Wiley & Sons. p. 42.