वितरणात्मक जाली

गणित में, एक वितरणात्मक जाली एक जाली (क्रम) है जिसमें जुड़ने और मिलने की संक्रियाएं एक दूसरे पर वितरण करती हैं। ऐसी संरचनाओं के प्रोटोटाइप उदाहरण सेटों का संग्रह हैं जिनके लिए जाली संचालन सेट यूनियन (सेट सिद्धांत) और चौराहे (सेट सिद्धांत) द्वारा दिया जा सकता है। वास्तव में, सेट की ये जाली पूरी तरह से दृश्यों का वर्णन करती हैं: प्रत्येक वितरण जाली - समरूपता के क्रम में - सेट की ऐसी जाली के रूप में दी गई है।

परिभाषा

जैसा कि मनमाने ढंग से जाली के मामले में, कोई वितरणात्मक जाली एल पर विचार करना चुन सकता है या तो आदेश सिद्धांत या सार्वभौमिक बीजगणित की संरचना के रूप में। जाली (आदेश) पर लेख में दोनों विचारों और उनके पारस्परिक पत्राचार पर चर्चा की गई है। वर्तमान स्थिति में बीजगणितीय विवरण अधिक सुविधाजनक प्रतीत होता है।

एक जाली (L,∨,∧) 'वितरणात्मक' है यदि निम्नलिखित अतिरिक्त पहचान L में सभी x, y और z के लिए है:

x ∧ (y ∨ z) = (x ∧ y) ∨ (x ∧ z).

जाली को आंशिक रूप से ऑर्डर किए गए सेट के रूप में देखते हुए, यह कहता है कि मीट ऑपरेशन सीमा-संरक्षण फ़ंक्शन (ऑर्डर सिद्धांत) गैर-खाली परिमित जुड़ता है। यह जाली सिद्धांत का एक बुनियादी तथ्य है कि उपरोक्त स्थिति इसके द्वंद्व (आदेश सिद्धांत) के बराबर है:

x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z)   L में सभी x, y और z के लिए।

प्रत्येक जाली में, p≤q को हमेशा की तरह p∧q=p के रूप में परिभाषित करते हुए, असमानता x ∧ (y ∨ z) ≥ (x ∧ y) ∨ (x ∧ z) अपनी दोहरी असमानता x ∨ (y) के साथ-साथ रखती है ∧ z) ≤ (x ∨ y) ∧ (x ∨ z). यदि विपरीत असमानताओं में से एक भी कायम रहती है तो एक जाली वितरणात्मक होती है। आदेश सिद्धांत की अन्य वितरण स्थितियों के साथ इस स्थिति के संबंध पर अधिक जानकारी वितरण (आदेश सिद्धांत) पर लेख में पाई जा सकती है।

रूपवाद

वितरणात्मक जालकों का एक रूपवाद केवल एक जालक समरूपता है जैसा कि जाली (आदेश) पर लेख में दिया गया है, अर्थात एक फ़ंक्शन जो दो जाली संचालन के साथ संगत है। चूँकि जालकों का ऐसा रूपवाद जाली संरचना को सुरक्षित रखता है, परिणामस्वरूप यह वितरणशीलता को भी संरक्षित करेगा (और इस प्रकार वितरणात्मक जालकों का एक रूपवाद होगा)।

उदाहरण

यंग की जाली

वितरणात्मक जाली सर्वव्यापी हैं, बल्कि विशिष्ट संरचनाएं भी हैं। जैसा कि पहले ही उल्लेख किया गया है कि वितरणात्मक जालकों का मुख्य उदाहरण सेटों के जालक हैं, जहां जुड़ना और मिलना सामान्य सेट-सैद्धांतिक संचालन द्वारा दिया जाता है। आगे के उदाहरणों में शामिल हैं:

• अधिकांश तर्कों का लिंडेनबाम-टार्स्की बीजगणित जो तार्किक संयोजन और तार्किक विच्छेदन का समर्थन करता है, एक वितरणात्मक जाली है, अर्थात और ऊपर या और इसके विपरीत वितरित करता है।
• प्रत्येक बूलियन बीजगणित (संरचना) एक वितरणात्मक जाली है।
• प्रत्येक हेयटिंग बीजगणित एक वितरणात्मक जालक है। विशेष रूप से इसमें सभी पूर्ण हेयटिंग बीजगणित और इसलिए टोपोलॉजिकल स्पेस स्थान के सभी खुले सेट लैटिस शामिल हैं। यह भी ध्यान दें कि हेयटिंग बीजगणित को अंतर्ज्ञानवादी तर्क के लिंडेनबाम बीजगणित के रूप में देखा जा सकता है, जो उन्हें पहले उदाहरण का एक विशेष मामला बनाता है।
• प्रत्येक कुल ऑर्डर एक वितरणात्मक जाली है जिसमें अधिकतम जोड़ और न्यूनतम पूरा होता है।
• प्राकृतिक संख्याएँ सबसे बड़े सामान्य भाजक को मिलन के रूप में और सबसे छोटे सामान्य गुणज को जोड़ के रूप में लेकर एक (सशर्त रूप से पूर्ण) वितरणात्मक जाली बनाती हैं। इस जाली में न्यूनतम तत्व भी है, अर्थात् 1, जो इसलिए जुड़ने के लिए पहचान तत्व के रूप में कार्य करता है।
• एक धनात्मक पूर्णांक n दिया गया है, n के सभी धनात्मक विभाजकों का समुच्चय एक वितरणात्मक जालक बनाता है, जिसमें फिर से सबसे बड़ा सामान्य भाजक मिलन के रूप में और सबसे छोटा सामान्य गुणज जोड़ के रूप में होता है। यह एक बूलियन बीजगणित है यदि और केवल यदि n वर्ग-मुक्त पूर्णांक|वर्ग-मुक्त है।
• एक रिज़्ज़ स्थान|जाली-क्रमित वेक्टर स्पेस एक वितरणात्मक जाली है।
• यंग आरेख के समावेशन क्रम द्वारा दी गई यंग की जाली#विभाजन (संख्या सिद्धांत) का प्रतिनिधित्व करने वाले आरेख एक वितरणात्मक जाली है।
• एक वितरणात्मक पॉलीटोप के बिंदु (एक उत्तल पॉलीटोप जो समन्वय के अनुसार न्यूनतम और समन्वय के अनुसार अधिकतम संचालन के तहत बंद होता है), इन दो संचालन के साथ जाली के जुड़ने और मिलने के संचालन के रूप में।

जाली सिद्धांत के विकास के आरंभ में चार्ल्स एस. पीयर्स का मानना ​​था कि सभी जाली वितरणात्मक हैं, यानी, वितरण बाकी जाली सिद्धांतों से चलता है। हालाँकि, स्वतंत्रता गणितीय प्रमाण अर्न्स्ट श्रोडर (गणितज्ञ) द्वारा दिए गए थे|श्रोडर, वोइगट,^{(:de:एंड्रियास हेनरिक वोइगट)} जैकब लुरोथ|लुरोथ, एल्विन कोर्सेल्ट, और रिचर्ड डेडेकाइंड।

विशेष गुण

उपरोक्त परिभाषा के विभिन्न समकक्ष सूत्र मौजूद हैं। उदाहरण के लिए, L वितरणात्मक है यदि और केवल यदि निम्नलिखित L में सभी तत्वों x, y, z के लिए मान्य हो:

(एक्स$\wedge$और)$\vee$(और$\wedge$साथ)$\vee$(साथ$\wedge$एक्स) = (एक्स$\vee$और)$\wedge$(और$\vee$साथ)$\wedge$(साथ$\vee$एक्स)।

इसी प्रकार, L वितरणात्मक है यदि और केवल यदि

एक्स$\wedge$z = y$\wedge$जेड और एक्स$\vee$z = y$\vee$z सदैव x=y दर्शाता है।

<गैलरी कैप्शन= दो प्रोटोटाइप गैर-वितरणात्मक जालकों के हस्से आरेख संरेखित=केंद्र > Image:M3 1xyz0.svg|हीरे की जाली एम₃ गैर-वितरणात्मक है: x ∧ (y ∨ z) = x ∧ 1 = x ≠ 0 = 0 ∨ 0 = (x ∧ y) ∨ (x ∧ z). Image:N5 1xyz0.svg|पंचकोणीय जाली एन₅ गैर-वितरणात्मक है: x ∧ (y ∨ z) = x ∧ 1 = x ≠ z = 0 ∨ z = (x ∧ y) ∨ (x ∧ z). </गैलरी>

वितरणात्मक जाली जिसमें उपसमुच्चय के रूप में N5 (ठोस रेखाएँ, बाएँ) और M3 (दाएँ) शामिल हैं, लेकिन उप-जाल के रूप में नहीं

सबसे सरल गैर-वितरणात्मक जालक M हैं₃, हीरे की जाली, और एन₅, पंचकोणीय जाली . एक जाली वितरणात्मक होती है यदि और केवल तभी जब इसका कोई भी उप-जाल एम के समरूपी न हो₃ या एन₅; एक सबलैटिस एक उपसमुच्चय है जो मूल जाली के मिलने और जुड़ने के संचालन के तहत बंद होता है। ध्यान दें कि यह एक उपसमुच्चय के समान नहीं है जो मूल क्रम के तहत एक जाली है (लेकिन संभवतः अलग-अलग जुड़ने और मिलने के संचालन के साथ)। आगे के लक्षण अगले भाग में प्रतिनिधित्व सिद्धांत से प्राप्त होते हैं।

इसी तथ्य को बताने का एक वैकल्पिक तरीका यह है कि प्रत्येक वितरणात्मक जाली दो-तत्व बूलियन बीजगणित | दो-तत्व श्रृंखला की प्रतियों का एक उप-प्रत्यक्ष उत्पाद है, या वितरणात्मक जाली के वर्ग का एकमात्र उप-प्रत्यक्ष रूप से अघुलनशील बीजगणित सदस्य दो- तत्व श्रृंखला. परिणाम के रूप में, प्रत्येक बूलियन बीजगणित (संरचना) में भी यह गुण होता है। अंततः वितरण में कई अन्य सुखद गुण शामिल होते हैं। उदाहरण के लिए, एक वितरणात्मक जाली का एक तत्व है लैटिस (ऑर्डर)#महत्वपूर्ण लैटिस-सैद्धांतिक धारणाएं|मीट-प्राइम यदि और केवल यदि यह लैटिस (ऑर्डर)#महत्वपूर्ण जाली-सैद्धांतिक धारणाएं|मीट-इरेड्यूसिबल है, हालांकि उत्तरार्द्ध में है सामान्यतः एक कमज़ोर संपत्ति। द्वंद्व के अनुसार, लैटिस (ऑर्डर)#महत्वपूर्ण लैटिस-सैद्धांतिक धारणाएं|जॉइन-प्राइम और लैटिस (ऑर्डर)#महत्वपूर्ण लैटिस-सैद्धांतिक धारणाएं|जॉइन-इरेड्यूसिबल तत्वों के लिए भी यही सच है। यदि एक जाली वितरणात्मक है, तो इसका आवरण संबंध एक माध्यिका ग्राफ बनाता है। इसके अलावा, प्रत्येक वितरण जाली भी मॉड्यूलर जाली है।

प्रतिनिधित्व सिद्धांत

परिचय ने पहले से ही वितरणात्मक जालकों के लिए सबसे महत्वपूर्ण लक्षण वर्णन पर संकेत दिया है: एक जालक वितरणात्मक है यदि और केवल यदि यह सेट के जालक के लिए आइसोमोर्फिक है (संघ (सेट सिद्धांत) और इंटरसेक्शन (सेट सिद्धांत) के तहत बंद)। (बाद वाली संरचना को कभी-कभी इस संदर्भ में सेटों की अंगूठी कहा जाता है।) उपरोक्त अर्थ में सेट यूनियन और इंटरसेक्शन वास्तव में वितरणात्मक हैं, यह एक प्राथमिक तथ्य है। दूसरी दिशा कम तुच्छ है, इसमें नीचे बताए गए प्रतिनिधित्व प्रमेयों की आवश्यकता होती है। इस लक्षण वर्णन से महत्वपूर्ण अंतर्दृष्टि यह है कि जो पहचान (समीकरण) सभी वितरणात्मक अक्षांशों में होती हैं, वे बिल्कुल वही होती हैं जो उपरोक्त अर्थ में सेट के सभी अक्षांशों में होती हैं।

वितरणात्मक जालकों के लिए बिरखॉफ के प्रतिनिधित्व प्रमेय में कहा गया है कि प्रत्येक परिमित वितरण जालक अपने जॉइन-प्राइम (समकक्ष रूप से: जुड़ने-इरेड्यूसिबल) तत्वों के आंशिक रूप से आदेशित सेट के ऊपरी सेट के जाली के लिए आइसोमोर्फिक है। यह सभी परिमित पोसेट्स के वर्ग और सभी परिमित वितरण जालकों के वर्ग के बीच एक आक्षेप (समाकृतिकता तक) स्थापित करता है। इस आक्षेप को परिमित वितरण जालकों की समरूपताओं और परिमित पोसेट्स के मोनोटोनिक कार्यों के बीच श्रेणियों की तुल्यता तक बढ़ाया जा सकता है। हालाँकि, इस परिणाम को अनंत जालकों में सामान्यीकृत करने के लिए और संरचना जोड़ने की आवश्यकता होती है।

एक अन्य प्रारंभिक प्रतिनिधित्व प्रमेय को अब वितरणात्मक जालकों के लिए स्टोन के प्रतिनिधित्व प्रमेय के रूप में जाना जाता है (यह नाम मार्शल हार्वे स्टोन का सम्मान करता है, जिन्होंने पहली बार इसे साबित किया था)। यह कुछ टोपोलॉजिकल स्पेस के सघन स्थान ओपन सेट सेट के लैटिस के रूप में वितरणात्मक लैटिस की विशेषता बताता है। इस परिणाम को बूलियन बीजगणित के लिए स्टोन के प्रसिद्ध स्टोन के प्रतिनिधित्व प्रमेय के सामान्यीकरण और स्टोन द्वैत की सामान्य सेटिंग की विशेषज्ञता के रूप में देखा जा सकता है।

हिलेरी प्रीस्टले द्वारा वितरणात्मक जाली के लिए प्रीस्टले के प्रतिनिधित्व प्रमेय में एक और महत्वपूर्ण प्रतिनिधित्व स्थापित किया गया था। इस सूत्रीकरण में, एक वितरणात्मक जाली का उपयोग इसके बिंदुओं पर एक अतिरिक्त आंशिक क्रम के साथ एक टोपोलॉजिकल स्पेस का निर्माण करने के लिए किया जाता है, जो बूलियन बीजगणित (या प्रीस्टले स्थान ) के लिए (पूरी तरह से ऑर्डर-पृथक) स्टोन के प्रतिनिधित्व प्रमेय का आदेश देता है। मूल जाली को इस स्थान के निचले सेट के क्लोपेन सेट के संग्रह के रूप में पुनर्प्राप्त किया गया है।

स्टोन और प्रीस्टली के प्रमेयों के परिणामस्वरूप, कोई भी आसानी से देख सकता है कि कोई भी वितरणात्मक जाली वास्तव में सेट की जाली के लिए समरूपी है। हालाँकि, दोनों कथनों के प्रमाण के लिए बूलियन प्राइम आदर्श प्रमेय की आवश्यकता होती है, जो पसंद के स्वयंसिद्ध का एक कमजोर रूप है।

निःशुल्क वितरणात्मक जाली

शून्य, एक, दो और तीन जनरेटर पर निःशुल्क वितरण जाली। 0 और 1 लेबल वाले तत्व खाली जुड़ते और मिलते हैं, और बहुमत लेबल वाला तत्व (x ∧ y) ∨ (x ∧ z) ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z) ∧ ( y ∨ z).

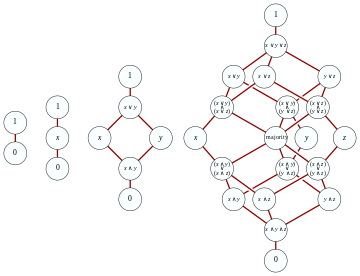
जनरेटर G के एक सेट पर मुक्त वस्तु वितरण जाली का निर्माण सामान्य मुक्त जाली की तुलना में अधिक आसानी से किया जा सकता है। पहला अवलोकन यह है कि, वितरण के नियमों का उपयोग करते हुए, प्रत्येक पद द्विआधारी संक्रियाओं द्वारा बनता है $\lor$ और $\land$ जनरेटर के एक सेट को निम्नलिखित समतुल्य सामान्य रूप में परिवर्तित किया जा सकता है:

$M_{1}\lor M_{2}\lor \cdots \lor M_{n},$

कहाँ $M_{i}$ जी के तत्वों के परिमित मिलन हैं। इसके अलावा, चूँकि मिलना और जुड़ना दोनों साहचर्य, क्रमपरिवर्तनशीलता और नपुंसकता हैं, कोई डुप्लिकेट और ऑर्डर को अनदेखा कर सकता है, और सेट के सेट के रूप में उपरोक्त की तरह मीट के जुड़ाव का प्रतिनिधित्व कर सकता है:

$\{N_{1},N_{2},\ldots ,N_{n}\},$

जहां $N_{i}$ जी के परिमित उपसमुच्चय हैं। हालाँकि, यह अभी भी संभव है कि ऐसे दो शब्द वितरण जालक के एक ही तत्व को दर्शाते हैं। ऐसा तब होता है जब सूचकांक j और k ऐसे होते हैं $N_{j}$ का एक उपसमुच्चय है $N_{k}.$ इस मामले में की मुलाकात $N_{k}$ की मुलाकात से नीचे होगा $N_{j},$ और इसलिए कोई भी अनावश्यक सेट को सुरक्षित रूप से हटा सकता है $N_{k}$ पूरे शब्द की व्याख्या बदले बिना। परिणामस्वरूप, G के परिमित उपसमुच्चय के एक समुच्चय को उसके सभी तत्वों को निरर्थक कहा जाएगा $N_{i}$ परस्पर अतुलनीय हैं (उपसमुच्चय क्रम के संबंध में); अर्थात्, जब यह एक स्पर्नर परिवार बनाता है।

अब जेनरेटर जी के एक सेट पर मुफ्त वितरण जाली को जी के परिमित उपसमुच्चय के सभी परिमित अप्रासंगिक सेटों के सेट पर परिभाषित किया गया है। दो परिमित अप्रासंगिक सेटों का जोड़ सभी अनावश्यक सेटों को हटाकर उनके संघ से प्राप्त किया जाता है। इसी प्रकार दो समुच्चयों S और T का मिलन इसका अप्रासंगिक संस्करण है $\{N\cup M\mid N\in S,M\in T\}.$ यह सत्यापन कि यह संरचना आवश्यक सार्वभौमिक संपत्ति के साथ एक वितरणात्मक जाली है, नियमित है।

एन जनरेटर के साथ मुक्त वितरण जाली में तत्वों की संख्या डेडेकाइंड संख्याओं द्वारा दी गई है। ये संख्याएँ तेज़ी से बढ़ती हैं, और केवल n≤9 के लिए जानी जाती हैं; वे हैं

2, 3, 6, 20, 168, 7581, 7828354, 2414682040998, 56130437228687557907788, 286386577668298411128469151667598498812366 (sequence A000372 in the OEIS).

उपरोक्त संख्याएँ मुक्त वितरण जालकों में तत्वों की संख्या की गणना करती हैं जिनमें जाली संचालन खाली सेट सहित तत्वों के परिमित सेटों से जुड़ते और मिलते हैं। यदि खाली जोड़ और खाली मिलन की अनुमति नहीं है, तो परिणामी मुक्त वितरण जालक में दो कम तत्व होते हैं; उनके तत्वों की संख्या अनुक्रम बनाती है

0, 1, 4, 18, 166, 7579, 7828352, 2414682040996, 56130437228687557907786, 286386577668298411128469151667598498812364 (sequence A007153 in the OEIS).

यह भी देखें

• पूर्णतः वितरणात्मक जाली - एक जाली जिसमें अनंत जोड़ अनंत मिलन पर वितरित होते हैं
• वितरणात्मक जालकों के लिए द्वैत सिद्धांत
• वर्णक्रमीय स्थान

अग्रिम पठन

• Burris, Stanley N.; Sankappanavar, H.P. (1981). A Course in Universal Algebra. Springer-Verlag. ISBN 3-540-90578-2.
• OEIS sequence A006982 (Number of unlabeled distributive lattices with n elements)