Difference between revisions of "समीकरण"

From alpha
Jump to navigation Jump to search
(Index created)
 
(45 intermediate revisions by 5 users not shown)
Line 1: Line 1:
== समीकरण बनाना ==
{{Short description|Mathematical formula expressing equality}}
किसी भी प्रकार के समीकरण([[Equations]]) के वास्तविक समाधान की ओर बढ़ने से पहले, इसे हल के लिए तैयार करने के लिए कुछ प्रारंभिक संक्रियाओं को करना आवश्यक है।
{{other uses}}
{{Multiple issues|
{{Lead too long|date=July 2022}}
{{More citations needed|date=July 2022}}
}}
[[File:First Equation Ever.png|thumb|right|300px|आधुनिक अंकन में 14x + 15 = 71 के समतुल्य एक बराबर चिह्न का पहला उपयोग। वेल्स के रॉबर्ट रिकॉर्डे द्वारा द वेटस्टोन ऑफ़ विट से (1557)।<ref name="Whetstone"/>]]गणित में, एक समीकरण एक [[सूत्र]] है जो दो व्यंजकों (गणित) की [[समानता (गणित)]] को बराबर के चिह्न {{char|1==}} से जोड़कर व्यक्त करता है। <ref name=":1">{{Cite web|title=समीकरण - गणित खुला संदर्भ|url=https://www.mathopenref.com/equation.html|access-date=2020-09-01|website=www.mathopenref.com}}</ref><ref>{{Cite web|title=समीकरण और सूत्र|url=https://www.mathsisfun.com/algebra/equation-formula.html|access-date=2020-09-01|website=www.mathsisfun.com}}</ref> अन्य भाषाओं में शब्द समीकरण और इसके सजातीय अर्थों में सूक्ष्म रूप से भिन्न अर्थ हो सकते हैं; उदाहरण के लिए, फ्रांसीसी भाषा में एक समीकरण को एक या एक से अधिक [[चर (गणित)]] के रूप में परिभाषित किया जाता है, जबकि [[अंग्रेजी भाषा]] में, बराबर चिह्न से संबंधित दो अभिव्यक्तियों से युक्त कोई भी अच्छी तरह से तैयार सूत्र एक समीकरण है।<ref>{{cite web |last1=Marcus |first1=Solomon |last2=Watt |first2=Stephen M. |title=एक समीकरण क्या है?|url=https://www.academia.edu/3287674 |access-date=2019-02-27 }}</ref>
चर वाले समीकरण को हल करने में यह निर्धारित करना सम्मिलित है कि चर के कौन से मान समानता को सत्य बनाते हैं। वे चर जिनके लिए समीकरण को हल करना होता है, 'अज्ञात' भी कहलाते हैं, और अज्ञात के वे मान जो समानता को संतुष्ट करते हैं, समीकरण के हल (समीकरण) कहलाते हैं। समीकरण दो प्रकार के होते हैं: [[पहचान (गणित)|सर्वसमिका (गणित)]] और सशर्त समीकरण। चर के सभी मूल्यों के लिए एक सर्वसमिका सत्य है। सशर्त समीकरण केवल चरों के विशेष मानों के लिए सत्य होता है।<ref>{{cite book
|chapter-url=http://www.universalis.fr/encyclopedie/NT01240/EQUATION_mathematique.htm
|chapter=Équation, mathématique
|first=Gilles|last=Lachaud
|title=यूनिवर्सल एनसाइक्लोपीडिया|language=fr
}}</ref><ref>"A statement of equality between two expressions. Equations are of two types, '''identities''' and '''conditional equations''' (or usually simply "equations")". « ''Equation'' », in ''{{Lang|en|Mathematics Dictionary}}'', {{ill|Glenn James (mathematician)|lt=Glenn James|de|Glenn James}} et [[Robert C. James]] (éd.), Van Nostrand, 1968, 3 ed. 1st ed. 1948, {{p.|131}}.</ref>


अभी भी अधिक प्रारंभिक कार्य प्रस्तावित समस्या की स्थितियों से समीकरण (''समी-करण, समी-करा या समी-क्रिया''; ''समा, बराबर'' और ''कर्''  से करना; इसलिए शाब्दिक रूप से, समान बनाना) बनाने का है। इस तरह के प्रारंभिक कार्य के लिए बीजगणित या अंकगणित के एक या एक से अधिक मौलिक संचालन के आवेदन की आवश्यकता हो सकती है।
एक समीकरण को दो व्यंजकों (गणित) के रूप में लिखा जाता है, जो बराबर चिह्न (=) से जुड़ा होता है।<ref name=":1" /> बराबर के चिह्न वाले समीकरण के दोनों पक्षों के व्यंजक समीकरण के बाएँ पक्ष और दाएँ पक्ष कहलाते हैं। बहुत बार किसी समीकरण के दाहिने पक्ष को शून्य मान लिया जाता है। यह मानने से व्यापकता कम नहीं होती है, क्योंकि इसे दोनों पक्षों से दाहिनी ओर घटाकर महसूस किया जा सकता है।


भास्कर द्वितीय कहते हैं: "''यावत्-तावत्'' " को अज्ञात मात्रा के मूल्य के रूप में माना जाता है। फिर जैसा कि विशेष रूप से बताया गया है-एक समीकरण के दो बराबर पक्षों को घटाना, जोड़ना, गुणा करना या विभाजित करना बहुत सावधानी से बनाया जाना चाहिए।
सबसे सामान्य प्रकार का समीकरण एक [[[[बहुपद]] समीकरण]] है (सामान्यतः इसे बीजगणितीय समीकरण भी कहा जाता है) जिसमें दो पक्ष बहुपद होते हैं। एक बहुपद समीकरण के पक्षों में एक या एक से अधिक योग संकेत और शब्दावली होती है। उदाहरण के लिए, समीकरण


== बीजीय व्यंजक और बीजीय समीकरण ==
:<math> Ax^2 +Bx + C - y = 0 </math>
बीजीय व्यंजक को निम्न उदाहरण <ref>''A Primer to Bhāratīya Gaṇitam , Bhāratīya-Gaṇita-Praveśa- Part-1''. Samskrit Promotion Foundation. 2021. [[ISBN (identifier)|ISBN]] [[Special:BookSources/978-81-951757-2-7|<bdi>978-81-951757-2-7</bdi>]].</ref>से समझा जा सकता है।
बाईं ओर <math> Ax^2 +Bx + C - y </math> है, जिसमें चार पद हैं, और दाहिनी ओर, केवल एक शब्द से मिलकर <math> 0 </math> है। चर (गणित) के नाम बताते हैं कि {{math|''x''}} और {{math|''y''}} अज्ञात हैं, और वह  {{math|''A''}}, {{math|''B''}}, और {{math|''C''}} मापदण्ड हैं, लेकिन यह सामान्य रूप से संदर्भ द्वारा तय किया जाता है (कुछ संदर्भों में, {{mvar|y}} एक मापदण्ड हो सकता है, या {{math|''A''}}, {{math|''B''}}, और {{math|''C''}} साधारण चर हो सकते हैं)।


राम कहता  है कि उसके पास 10 सिक्के श्याम से ज्यादा हैं। हम ठीक से नहीं जानते कि श्याम के पास कितने सिक्के  हैं। उसके पास कितने भी सिक्के हो सकते हैं। लेकिन हम जानते हैं कि राम के सिक्कों  की संख्या = श्याम  के कंचों की संख्या + 10
एक समीकरण उस पैमाने के अनुरूप होता है जिसमें वजन रखा जाता है। जब किसी चीज़ के बराबर वज़न (जैसे, अनाज) को दो पलड़ों में रखा जाता है, तो दो वज़न तराजू को संतुलन में रखते हैं और उन्हें बराबर कहा जाता है। यदि पलड़े के एक पलड़े में से अन्न की गिनती निकाली जाए, तो पलड़े को सन्तुलित रखने के लिथे दूसरे पलड़े में से भी उतना ही अन्न निकाला जाए। अधिक सामान्यतः, एक समीकरण संतुलन में रहता है यदि इसके दोनों पक्षों पर एक ही संचालन किया जाता है।


हम 'श्याम  के सिक्कों की संख्या' को अक्षर x से निरूपित करेंगे। यहाँ x अज्ञात है जो 1, 2, 3, 4 आदि हो सकता है।
कार्तीय ज्यामिति में, ज्यामितीय आकृतियों का वर्णन करने के लिए समीकरणों का उपयोग किया जाता है। जैसा कि जिन समीकरणों पर विचार किया जाता है, जैसे [[निहित समीकरण]] या [[पैरामीट्रिक समीकरण|प्राचलिक समीकरण]], के असीम रूप से कई समाधान होते हैं, उद्देश्य अब अलग है: समाधानों को स्पष्ट रूप से देने या उन्हें गिनने के बजाय, जो असंभव है, आंकड़ों के गुणों का अध्ययन करने के लिए समीकरणों का उपयोग किया जाता है। यह बीजगणितीय ज्यामिति का प्रारंभिक विचार है, जो गणित का एक महत्वपूर्ण क्षेत्र है।


x का प्रयोग करके हम लिखते हैं,
बीजगणित समीकरणों के दो मुख्य परिवारों का अध्ययन करता है: [[बहुपद समीकरण]] और उनमें से, रैखिक समीकरणों का विशेष मामला। चूंकि जिन समीकरणों पर विचार किया जाता है, जैसे अंतर्निहित समीकरण या प्राचलिक समीकरण, उनके असीम रूप से कई समाधान होते हैं, उद्देश्य अब अलग है: समाधानों को स्पष्ट रूप से देने या उन्हें गिनने के बजाय, जो असंभव है, आंकड़ों के गुणों का अध्ययन करने के लिए समीकरणों का उपयोग किया जाता है। बीजगणित [[डायोफैंटाइन समीकरण|डायोफैंटाइन]] समीकरणों का भी अध्ययन करता है जहां गुणांक और समाधान पूर्णांक होते हैं। उपयोग की जाने वाली तकनीकें भिन्न हैं और [[संख्या सिद्धांत]] से आती हैं। ये समीकरण सामान्य तौर पर कठिन होते हैं; कोई प्रायः समाधान के अस्तित्व या अनुपस्थिति को खोजने के लिए खोज करता है, और यदि वे मौजूद हैं, तो समाधानों की संख्या गिनने के लिए मौजूद हैं।


राम के सिक्कों की संख्या = x+10
[[विभेदक समीकरण]] ऐसे समीकरण होते हैं जिनमें एक या अधिक कार्य और उनके व्युत्पादित सम्मिलित होते हैं। वे उस फलन के लिए एक व्यंजक खोज कर हल किए जाते हैं जिसमें अवकलज सम्मिलित नहीं है। विभेदक समीकरणों का उपयोग  प्रतिरूप प्रक्रियाओं के लिए किया जाता है जिसमें चर के परिवर्तन की दर सम्मिलित होती है, और भौतिकी, रसायन विज्ञान, जीव विज्ञान और अर्थशास्त्र जैसे क्षेत्रों में उपयोग किया जाता है।


अत: 'x + 10' एक बीजीय व्यंजक है।
= प्रतीक, जो हर समीकरण में प्रकट होता है, का आविष्कार 1557 में रॉबर्ट रिकॉर्डे द्वारा किया गया था, जिन्होंने माना था कि समान लंबाई वाली समानांतर सीधी रेखाओं से अधिक समान कुछ भी नहीं हो सकता है।<ref name="Whetstone">Recorde, Robert, ''The Whetstone of Witte'' ... (London, England: {{not a typo|Jhon}} Kyngstone, 1557), [https://archive.org/stream/TheWhetstoneOfWitte#page/n237/mode/2up the third page of the chapter "The rule of equation, commonly called Algebers Rule."]</ref>


प्रतीकों के प्रयोग में बीजगणित प्रचुर मात्रा में है। ये प्रतीक अज्ञात मात्राओं और उनके साथ किए गए कार्यों का प्रतिनिधित्व करते हैं। निम्नलिखित तालिका में वे प्रतीक दिए गए हैं जिनका उपयोग प्राचीन भारतीय गणितज्ञों द्वारा कुछ बुनियादी कार्यों के लिए किया गया था।
{| class="wikitable"
|+
!क्रमांक
!बीजीय व्यंजक का संघटक
! संस्कृत शब्द
!प्रतीक/चिह्न
!उदाहरण
!
|-
| 1
|अज्ञात
|यावत्तावत्
कालकः


नीलकः , ......
== परिचय ==
|या
का


नी , ........
=== अनुरूप चित्रण ===
|या ३
का ४


नी ८
[[File:Equation illustration colour.svg|thumb|एक साधारण समीकरण का चित्रण; x, y, z वास्तविक संख्याएँ हैं, जो वज़न के समान हैं।]]एक समीकरण एक वजनी पैमाने, तराजू या झूले के समान होता है।
|3x
4y


8z
समीकरण का प्रत्येक पक्ष संतुलन के एक पक्ष से मेल खाता है। प्रत्येक पक्ष पर अलग-अलग मात्राएँ रखी जा सकती हैं: यदि दोनों पक्षों पर भार समान हैं, तो तराजू संतुलित करता है, और सादृश्यता में, संतुलन का प्रतिनिधित्व करने वाली समानता भी संतुलित होती है (यदि नहीं, तो संतुलन की कमी एक [[असमानता]] से मेल खाती है ( गणित) एक असमिका द्वारा दर्शाया गया है)।
|-
|2
|योगफल
|योगः
|<nowiki>-</nowiki>
|या का
या ३ का ४
|x + y
3x + 4y
|-
|3
|गुणनफल
|भावितम्
|भा
|याकाभा
याकाभा ३
|xy
3xy
|-
| 4
|वर्ग
| वर्गः
|व
|याव
|x<sup>2</sup>
|-
|5
| घनक्षेत्र
|घनः
|घ
|याघ
|x<sup>3</sup>
|-
|6
|चौथी शक्ति
|वर्ग​-वर्गः
|वव
|यावव
|x<sup>4</sup>
|-
|7
|स्थायी अवधि
|रूपम्
|रू
|रू ३
|3
|-
|8
|ऋणात्मक
|ऋणम्
| मात्रा के ऊपर बिंदु  (.)
|'''.'''
रू ४
|<nowiki>-4</nowiki>
|}


उदाहरण में, x, y और z सभी अलग-अलग मात्राएँ हैं (इस मामले में वास्तविक संख्याएँ) जिन्हें गोलाकार भार के रूप में दर्शाया गया है, और x, y और z में से प्रत्येक का अलग-अलग वज़न है। योग वजन जोड़ने के अनुरूप है, जबकि घटाव पहले से मौजूद वजन को हटाने से मेल खाता है। जब समानता धारण करती है, तो प्रत्येक पक्ष का कुल भार समान होता है।


===मापदण्ड एवं अपरिचित ===
{{see also|अभिव्यक्ति (गणित)}}


अक्षर ''या'' (''यावत्-तावत्'' का संक्षिप्त रूप) अज्ञात मात्रा का सबसे लोकप्रिय प्रतिनिधित्व था। इसके वर्ग को यव कहा जाता था, जो ''यावत्-तावत्-वर्ग'' (वर्ग का अर्थ वर्ग) का संक्षिप्त नाम था। समीकरण लिखते समय, अचर पद को ''रू'' अक्षर से निरूपित किया जाता था, जो रूपा  का एक संक्षिप्त नाम है जैसा कि ऊपर दी गई तालिका में देखा गया है। समीकरण में किसी भी ऋणात्मक चिह्न को पद के ऊपर एक बिंदु द्वारा दर्शाया जाता है।
समीकरणों में प्रायः अज्ञात के अतिरिक्त अन्य पद होते हैं। ये अन्य शब्द, जिन्हें ज्ञात माना जाता है, सामान्यतः स्थिरांक, गुणांक या मापदण्ड कहलाते हैं।


x और y को अज्ञात के रूप में सम्मिलित करने वाले समीकरण का एक उदाहरण और मापदण्ड R है


:<math> x^2 +y^2 = R^2 .</math>
जब R को 2 (R = 2) के मान के लिए चुना जाता है, तो इस समीकरण को कार्तीय निर्देशांक में मूल के चारों ओर 2 के त्रिज्या के चक्र के समीकरण के रूप में सर्वसमिकाा जाएगा। इसलिए, R अनिर्दिष्ट के साथ समीकरण चक्र के लिए सामान्य समीकरण है।


यदि किसी व्यंजक में तीन अज्ञात मात्राएँ हैं, तो प्रयुक्त चिह्न ''या'' , ''का'', और ''नी''   हैं। ये ''यावत्-तावत्,'' ''कालका'' और ''नीलका''  के संक्षिप्त रूप हैं। पहली दो अज्ञात मात्राओं के उत्पाद को ''याकाभा'' के रूप में दर्शाया जाता है जहाँ ''या'' और ''का'' दो अज्ञात हैं और ''भा''  उनके उत्पाद के लिए है।
सामान्यतः, अज्ञात को वर्णमाला के अंत में अक्षरों द्वारा दर्शाया जाता है, x, y, z, w, ..., जबकि गुणांक (मापदण्ड) शुरुआत में अक्षरों द्वारा दर्शाए जाते हैं, a, b, c, d, .. ... उदाहरण के लिए, सामान्य [[द्विघात समीकरण]] को सामान्यतः ax<sup>2</sup>+ bx+ c = 0  लिखा जाता है.


निम्नलिखित तालिका प्राचीन भारतीय गणितज्ञों द्वारा प्रयुक्त कुछ बीजीय व्यंजकों का निरूपण करती है।
समाधान खोजने की प्रक्रिया, या, मापदंडों के मामले में, अज्ञात को मापदंडों के संदर्भ में व्यक्त करना, [[समीकरण हल करना]] कहलाता है। मापदंडों के संदर्भ में समाधानों की ऐसी अभिव्यक्तियाँ भी समाधान कहलाती हैं।
{| class="wikitable"
|+
!क्रमांक
!आधुनिक संकेतन
!प्राचीन भारतीय संकेतन
|-
|1
|x + 1
|या १ रू १
|-
|2
|3x - 7
|या ३ रू ७<sup>'''.'''</sup>
|-
|3
|2x – 8
|या २ रू ८<sup>'''.'''</sup>
|-
|4
|15x<sup>2</sup> + 7x - 2
|याव १५ या ७ रू २<sup>'''.'''</sup>
|-
|5
|1x<sup>4</sup> + 6x<sup>3</sup> + 25x<sup>2</sup> + 48x + 64
|यावव १ याघ ६ याव २५ या ४८ रू ६४
|-
|6
|18x<sup>2</sup> + 12xy - 6xz -6x
|याव १८ याकाभा १२ यानीभा ६<sup>'''.'''</sup> या ६<sup>'''.'''</sup>
|}


 
समीकरणों की एक प्रणाली एक साथ समीकरणों का एक सम्मुच्चय है, सामान्यतः कई अविदित में जिसके लिए सामान्य समाधान मांगे जाते हैं। इस प्रकार, प्रणाली का समाधान प्रत्येक अज्ञात के लिए मूल्यों का एक सम्मुच्चय है, जो एक साथ प्रणाली में प्रत्येक समीकरण का समाधान बनाते हैं। उदाहरण के लिए, प्रणाली
 
:<math>\begin{align}
हम देखेंगे कि प्राचीन भारतीय गणितज्ञों द्वारा बीजीय व्यंजक कैसे लिखे जाते हैं।
3x+5y&=2\\
 
5x+8y&=3
समीकरण 10x - 8 = x<sup>2</sup> +1 पर विचार करें
\end{align}
 
इसे इस प्रकार लिखा जा सकता है,
 
0x<sup>2</sup> + 10x - 8 = 1x<sup>2</sup> + 0x + 1
 
x<sup>2</sup>, x<sup>1</sup>, x<sup>0</sup> (स्थिर पद/अवधि) की स्थितियों का निरीक्षण करें। क्या आप कोई प्रतिरूप नोटिस कर सकते हैं? समीकरण लिखने का मानक तरीका x की उच्चतम घात से प्रारंभ होता है। तब x की घातों को उसके निम्नतम घात तक अवरोही क्रम में लिखा गया था। समीकरण लिखने के इस प्रारूप का अनुसरण प्राचीन काल से गणितज्ञों द्वारा किया जाता रहा है।
 
ब्रह्मगुप्त ने समीकरण को समकरण या संकरण कहा। इसका अर्थ है 'समान बनाना'। एक समीकरण के दो पक्षों (LHS और RHS) को एक के नीचे एक लिखा जाता है। प्रतीक '=' का प्रयोग नहीं किया गया था। एक समीकरण के दोनों पक्षों को अज्ञात के लिए उपयुक्त मान (मानों) को खोजने के द्वारा समान बनाया गया था।
 
हम देखेंगे कि यह समीकरण चतुर्वेद पृथूदकस्वामिन् (864 ईस्वी) ने ब्रह्म-स्फूट-सिद्धांत पर अपने भाष्य में कैसे लिखा था। वह समीकरण लिखते  हैं।
 
10x - 8 = x<sup>2</sup> + 1 इस प्रकार है:
{| class="wikitable"
|+
!देवनागरी
!लिप्यंतरण
!
!आधुनिक संकेतन
|-
|याव ०  या १०  रू ८'''<sup>.</sup>'''
याव १  या ०    रू १
|याव  0 या  10 rū 8'''<sup>.</sup>'''
याव  1 या  0 rū 1
|⇒
|0x<sup>2</sup> + 10 x - 8 = 1x<sup>2</sup> + 0x + 1
|}
भास्कर द्वितीय  के बीजगणित से समीकरण का एक और उदाहरण है:
 
x<sup>4</sup> - 2x<sup>2</sup> - 400x = 9999
 
इसे इस प्रकार दर्शाया गया है,
 
यावव १ याव २'''<sup>.</sup>'''   या  ४<sup>'''.'''</sup>०० रू ०
 
यावव ० याव ०   या  ०       रू ९९९९
 
== बीजीय व्यंजकों के साथ संक्रिया ==
 
 
 
भास्कर द्वितीय बीजगणितीय शब्दों का उपयोग करते हुए संक्रियाएँ इस प्रकार देते  हैं :
 
''स्याद्रूपवर्णाभिहतौ तु वर्णो द्वित्र्यादिकानां समजातिकानाम् ॥''
 
''वधे तु तद्वर्गघनादयः स्युस्तद्भावितं चासमजातिघाते।''
 
''भागादिकं रूपवदेव शेषं व्यक्ते यदुक्तं गणिते तदत्र ॥''<ref>Bījagaṇita, ch. Avyaktādi-guṇana, vs.6,7, p.8</ref>
 
"एक संख्यात्मक स्थिरांक और एक अज्ञात मात्रा का गुणनफल एक अज्ञात मात्रा है। दो या तीन समान पदों के गुणनफल उनके वर्ग या घन (क्रमशः) होते हैं। विषम पदों का गुणनफल भाविता है। भिन्न आदि ज्ञात के मामले में हैं। अन्य (प्रक्रियाएं) अंकगणित में वर्णित समान हैं।"
 
=== बीजीय व्यंजकों का जोड़ और घटाव ===
भास्कर  द्वितीय अज्ञात राशियों के जोड़ और घटाव का नियम इस प्रकार देते  हैं:
 
''योगोऽन्तरं तेषु समानजात्योर्विभिन्नजात्योश्च पृथक् स्थितिश्च।''<ref>Bījagaṇita ch. Avyakta-saṅkalana-vyavakalana, vs.6, p.7</ref>
 
"जोड़ और घटाव समान पदों के बीच किया जाता है। विपरीत शब्दों को अलग रखा जाना चाहिए।"
 
'''व्याख्या:'''
 
यह सर्वविदित है कि जोड़ और घटाव केवल समान पदों में ही किया जा सकता है और विपरीत पदों को अलग-अलग रखा जाना है। समान शब्द वे शब्द हैं जिनमें समान अक्षर चर होते हैं जो समान शक्तियों के लिए उठाए जाते हैं। उदा., या ३, या ४, या ५ समान पद हैं। याव २, याव ५, याव ७ भी समान पद  हैं। का ३, का ७, का १५ भी समान पद  हैं।आजकल हम कहते हैं कि 3x, 4x, 5x समान पद हैं। इसी प्रकार 2x<sup>2</sup>, 5x<sup>2</sup>, 7x<sup>2</sup> समान पद हैं। और 3y, 7y, 15y भी समान पद हैं। जब हमारे पास समान पद होते हैं, तो योग और अंतर को सरल बनाया जा सकता है। उदा. 3x + 5x को 8x के रूप में सरल बनाया जा सकता है। 10x<sup>2</sup> - 4x<sup>2</sup> को 6x<sup>2</sup> के रूप में सरल बनाया जा सकता है।
 
विपरीत पद वे पद हैं जिनमें भिन्न-भिन्न चर या भिन्न-भिन्न घात वाले चर होते हैं। उदा.या ३, याव ३, याघ ४, का ५, काव, याकाभा । आधुनिक संकेतन में, इन्हें 3x, 3x<sup>2</sup>, 4x<sup>3</sup>, 5y, y<sup>2</sup>, xy के रूप में दर्शाया जाता है।
 
=== बीजीय व्यंजकों का गुणन ===
बीजगणित गुणन का नियम देता है -
 
''गुण्यः पृथग्गुणकखण्डसमो निवेश्यस्तैः खण्डकैः क्रमहतः सहितो यथोक्त्या।''
 
''अव्यक्तवर्गकरणीगणनास चिन्त्यो व्यक्तोक्तखण्डगुणनाविधिरेवमत्र॥''<ref>Bījagaṇita ch. Avyaktādi-guṇana, vs.8, p.8</ref>
 
"गुणक को गुणक के पदों के रूप में कई स्थानों पर रखें। गुणक के पदों को अलग-अलग क्रम से गुणा करें और समस्या में निर्देशानुसार परिणाम जोड़ें। यह अज्ञात संख्याओं और सर्ड के वर्गों के मामले में भी लागू होता है। अंकगणितीय संख्याओं के मामले में बताई गई आंशिक उत्पादों की विधि यहां भी लागू होती है।"
 
'''व्याख्या'''
{| class="wikitable"
!प्राचीन भारतीय संकेतन
!आधुनिक संकेतन
|-
|यदि या ३ रू ५ और या ४ रू ७ क्रमशः गुणक और गुणक हैं,
उनका उत्पाद निम्नानुसार प्राप्त किया जा सकता है:
|यदि 3x + 5 और 4x + 7 क्रमशः गुणक और गुणक हैं,
 
उनका उत्पाद निम्नानुसार प्राप्त किया जा सकता है:
|-
|गुणक के दो पद होते हैं, अर्थात् या ४ and रू ७
|गुणक के दो पद हैं, अर्थात् 4x और 7
|-
|गुणक को दो स्थानों पर रखें। उन्हें गुणक के पदों से अलग से गुणा करें जैसा कि दिखाया गया है।
(या ३ रू ५) X या ४ = याव १२ या २०
 
(या ३ रू ५) X रू ७ = या २१ रू ३५
|गुणक को दो स्थानों पर रखें। उन्हें गुणक के पदों से अलग से गुणा करें जैसा कि दिखाया गया है।
(3x + 5) X 4x = 12x<sup>2</sup> + 20x
 
(3x + 5) X 7 = 21x + 35
|-
|परिणाम जोड़ें।
गुणन परिणाम है:: याव् १२ या ४१ रू ३५
|परिणाम जोड़ें।
 
गुणन परिणाम है: 12x<sup>2</sup> + 41x + 35
|}
 
 
 
यदि <math>ax + b</math> और <math>cx+d</math> क्रमशः गुणक और गुणक हैं, तो उनका गुणनफल निम्नानुसार प्राप्त किया जा सकता है:
 
गुणक के दो पद हैं, अर्थात् cx और d। गुणक को दो स्थानों पर रखें। उन्हें गुणक के पदों से अलग से गुणा करें जैसा कि दिखाया गया है।
 
<math>(ax+b) cx = acx^2+bcx</math>
 
<math>(ax+b)d = adx+bd</math>
 
परिणाम जोड़ें।
 
गुणन परिणाम है: <math>acx^2+(bc+ad)x+bd</math>
 
== समीकरणों का वर्गीकरण ==
ऐसा लगता है कि समीकरणों का सबसे पहला हिंदू वर्गीकरण उनकी डिग्री के अनुसार हुआ है, जैसे कि सरल (तकनीकी रूप से ''यावत्-तावत्''  (जितना या उतना ही, अर्थात् एक मनमानी  मात्रा) कहा जाता है), द्विघात ''(वर्ग)'', घन और द्विघात (''वर्ग-वर्ग'')। इसका संदर्भ लगभग 300 ईसा पूर्व के एक विहित कार्य में मिलता है। लेकिन आगे की प्रमाण के अभाव में, हम इसके बारे में सुनिश्चित नहीं हो सकते। ब्रह्मगुप्त (628) ने समीकरणों को इस प्रकार वर्गीकृत किया है: (I) एक अज्ञात में समीकरण (''एक-वर्ण-समीकरण''), (2) कई अज्ञात में समीकरण (''अनेक-वर्ण-समीकरण''), और (3) अज्ञात के उत्पादों से जुड़े समीकरण (''भैविता)'' )
 
प्रथम वर्ग को फिर से दो उप वर्गों में विभाजित किया गया है, अर्थात, (i) रैखिक समीकरण, और (ii) द्विघात समीकरण (''अव्यक्त-वर्ग-समीकरण'')। यहाँ से हमारे पास समीकरणों को उनकी डिग्री के अनुसार वर्गीकृत करने की हमारी वर्तमान पद्धति की शुरुआत है। चतुर्वेद पृथुदका स्वामी (860) द्वारा अपनाई गई वर्गीकरण पद्धति थोड़ी भिन्न है। उनके चार वर्ग हैं: (1) एक अज्ञात के साथ रैखिक समीकरण, (2) अधिक अज्ञात के साथ रैखिक समीकरण, (3) अपनी दूसरी और उच्च शक्तियों में एक, दो या अधिक अज्ञात के साथ समीकरण, और (4) अज्ञात के उत्पादों को शामिल करने वाले समीकरण . चूँकि तृतीय वर्ग के समीकरण को हल करने की विधि मध्य पद के उन्मूलन के सिद्धांत पर आधारित है, इसलिए उस वर्ग को ''मध्यमाहारण'' (मध्यम से-"मध्य", अहारण से -"उन्मूलन", इसलिए अर्थ "उन्मूलन मध्य अवधि का" कहा जाता है। )। अन्य वर्गों के लिए, ब्रह्मगुप्त द्वारा दिए गए पुराने नामों को बरकरार रखा गया है। वर्गीकरण की इस पद्धति का अनुसरण बाद के लेखकों ने किया है।
 
भास्कर द्वितीय तीसरे वर्ग में दो प्रकारों को अलग करता है, अर्थात (i) अपनी दूसरी और उच्च शक्तियों में एक अज्ञात में समीकरण और (ii) दूसरी और उच्च शक्तियों में दो या दो से अधिक अज्ञात वाले समीकरण।' कृष्ण के अनुसार (1580) समीकरण मुख्य रूप से दो वर्गों के होते हैं: (1) एक अज्ञात में समीकरण और (2) दो या दो से अधिक अज्ञात में समीकरण। वर्ग (1) में फिर से दो उपवर्ग होते हैं: (i) सरल समीकरण और ( ii) द्विघात और उच्च समीकरण। वर्ग (2) में तीन उपवर्ग हैं: (i) एक साथ रैखिक समीकरण, (ii) अज्ञात की दूसरी और उच्च शक्तियों वाले समीकरण, और (iii) अज्ञात के उत्पादों को शामिल करने वाले समीकरण। फिर वह देखता है कि इन पांच वर्गों को कक्षा (1) और (2) के दूसरे उपवर्गों को ''मध्यमाहारन''  के रूप में एक वर्ग में शामिल करके चार तक कम किया जा सकता है।
 
== एक अज्ञात में रैखिक समीकरण ==
एक रैखिक समीकरण एक समीकरण है जिसमें चर, गुणांक और स्थिरांक की केवल पहली शक्ति होती है। उदाहरण के लिए, समीकरण 2x + 4 = 5 एक चर में एक रैखिक समीकरण है। इसे प्रथम-क्रम समीकरण कहा जाता है क्योंकि चर (x) की घात एक है। यदि समीकरण में x की उच्चतम शक्ति दो के रूप में है, अर्थात x2 , तो यह एक द्विघात (द्वितीय क्रम) समीकरण होगा।
 
==== प्रारंभिक समाधान: ====
जैसा कि पहले ही कहा गया है, एक अज्ञात में एक रैखिक समीकरण का ज्यामितीय समाधान ''शुल्बसूत्र''; ''śulba'' में पाया जाता है, जिसमें से सबसे पहला 800 ईसा पूर्व के बाद का नहीं है। ''स्थानांग-सूत्र'' (सी। 300 ईसा पूर्व) में इसके नाम (''यावत्-तावत्'') से एक रैखिक समीकरण का संदर्भ है जो समाधान की विधि का सूचक है! उस समय अनुसरण किया गया । हालांकि, हमारे पास इसके बारे में और कोई प्रमाण नहीं है। सरल बीजगणितीय समीकरणों और उनके समाधान के लिए एक विधि से संबंधित समस्याओं के निस्संदेह मूल्य का सबसे पहला हिंदू रिकॉर्ड बख्शाली ग्रंथ में मिलता है, जो संभवतया ईसाई युग की शुरुआत के बारे में लिखा गया था।
 
एक समस्या यह है कि "पहले को दी गई राशि ज्ञात नहीं है। दूसरी को पहले की तुलना में दोगुना दिया जाता है, तीसरे को दूसरे से तीन गुना और चौथे को तीसरे से चार गुना अधिक दिया जाता है। वितरित की गई कुल राशि है 132. पहले की राशि क्या है?"
 
यदि x पहले को दी गई राशि हो, तो समस्या के अनुसार,
 
x + 2X + 6x + 24X = 132
 
==== असत्य स्थिति का नियम: ====
इस समीकरण का हल इस प्रकार दिया गया है:
 
"'किसी भी वांछित मात्रा को रिक्त स्थान पर रखना'; कोई भी वांछित मात्रा 1 है; 'फिर श्रृंखला का निर्माण करें।
{| class="wikitable"
|+
|1
|2
|2 3
|6 4
|-
|1
|1
|1 1
|1 1
|}
'गुणा किया हुआ'
{| class="wikitable"
|+
|1
|2
|6
|24
|}
जोड़ा गया' 33. "दृश्यमान मात्रा को विभाजित करें'
{| class="wikitable"
|+
|132
33
|}
(जो) कमी करने पर बन जाता है
{| class="wikitable"
|+
|4
1
|}
(यह है) दी गई राशि (पहले को)।"
 
बख्शाली ग्रंथ में समस्याओं के एक और सेट का समाधान अंततः ax+ b=p प्रकार के समीकरण की ओर ले जाता है। इसके समाधान के लिए दी गई विधि यह है कि x के लिए कोई मनमाना मान g रखा जाए, ताकि
 
ag+ b =p'  कहा जाए ।
 
तब सही मान होगा
 
<math>{\displaystyle x = {\frac{(p - p')}{a}} + g}</math>
 
==== रैखिक समीकरणों का हल ====
आर्यभट्ट (499) कहते हैं:
 
"दो व्यक्तियों से संबंधित ज्ञात "राशि" के अंतर को अज्ञात के गुणांकों के अंतर से विभाजित किया जाना चाहिए। यदि उनकी संपत्ति समान है, तो भागफल अज्ञात का मान होगा।"
 
यह नियम इस प्रकार की समस्या पर विचार करता है: दो व्यक्ति, जो समान रूप से समृद्ध हैं, के पास क्रमशः a, b एक निश्चित अज्ञात राशि का c, d के साथ एक साथ है।
 
नकद में पैसे की इकाइयों। वह राशि क्या है?
 
यदि x अज्ञात राशि हो, तो समस्या से
 
ax + c = bx+ d
 
इसलिए  <math>{\displaystyle x = {\frac{(d - c)}{(a- b)}}}</math>
 
जिस वजह से  नियम।
 
bx + c = dx + e के रूप के रैखिक समीकरण को हल करने का नियम जहाँ b, c, d और e दिए गए हैं, ब्रह्मगुप्त द्वारा निम्नानुसार दिया गया है।
 
 
 
''अव्यक्तान्तरभक्तं व्यस्ततां समानऽव्यक्तं।''
 
''कक्षा व्यक्ताः शोध यशद्रूपाणी तदधस्तात II ''<ref>Brāhma-sphuṭa-siddhānta, Ch 18, vs.43,p.314</ref>
 
 
 
"अज्ञात के अंतर से उल्टे और विभाजित निरपेक्ष संख्याओं का अंतर, एक समीकरण में अज्ञात का [मान] है।"
 
'''व्याख्या''': समीकरण पर विचार करें, bx + c = dx + e
 
यहाँ x अज्ञात राशि है जिसका मान ज्ञात करना है। अक्षर b और d इसके गुणांक हैं। शेष अक्षर c और e संख्यात्मक स्थिरांक हैं।
 
निरपेक्ष संख्याओं का अंतर = c-e
 
उल्टे पूर्ण संख्याओं का अंतर = e-c
 
अज्ञात के गुणांकों का अंतर = b - d
 
x के रूप में पाया जाता है
 
<math>{\displaystyle x  = {\frac {(e-c)}{(b-d)} }}</math>
 
 
भास्कर  द्वितीय  बताते हैं कि उपरोक्त सूत्र कैसे प्राप्त किया जाता है।
 
''यावत्तावत् कल्प्यमव्यक्तराशेर्मानं तस्मिन् कुर्वतोद्दिष्टमेव ।''
 
''तुल्यौ पक्षौ साधनीयौ प्रयत्नात्त्यक्त्वा क्षिप्त्वा वाऽपि संगुण्य भक्त्वा ॥''
 
''एकाव्यक्तं शोधयेदन्यपक्षाद्रूपाण्यन्यस्येतरस्माच्च पक्षात्''
 
''शेषाव्यक्तेनोद्धरेद्रूपशेषं व्यक्तं मानं जायतेऽव्यक्तराशेः''॥<ref>(Bijagaṇita, ch. Ekavarṇa-samīkaraṇa, vs.1, 2, pp.43,44)</ref>
 
"अज्ञात मात्रा (x) मान लें। रद्द करने या कम करने या गुणा करने या विभाजित करने के बाद अज्ञात शब्दों से जुड़े कारकों को एक तरफ और स्थिर शब्दों को दूसरी तरफ स्थानांतरित करके वांछित प्रक्रिया करें। अज्ञात के गुणांक से पदों को विभाजित करें और अज्ञात कारक के मान की गणना करें।"
 
'''व्याख्या''': उदाहरण के लिए, आइए हम निम्नलिखित समीकरण पर विचार करें:
 
6x - 5 = 2x + 3
 
(i) अज्ञात पदों वाले कारकों को एक तरफ और अचरों को दूसरी तरफ स्थानांतरित करने पर, हम प्राप्त करते हैं,
 
6x - 2x = 3 + 5
 
इसलिए, 4x = 8
 
ii) अज्ञात के गुणांक द्वारा पदों को विभाजित करने पर, हम प्राप्त करते हैं
 
x = 2
 
<s>ब्रह्मगुप्त कहते हैं:</s>
 
<s>"एक (रैखिक) समीकरण में एक अज्ञात में, ज्ञात शब्दों का अंतर उल्टे क्रम में लिया जाता है, अज्ञात के गुणांक के अंतर से विभाजित होता है</s>
 
<s>(अज्ञात का मूल्य है)।</s>
 
श्रीपति लिखते हैं:
 
"पहले ज्ञात पद को छोड़कर किसी भी पक्ष (समीकरण के) से अज्ञात को हटा दें; दूसरी तरफ उल्टा (किया जाना चाहिए)। गुणांक के अंतर से विभाजित उल्टे क्रम में लिए गए निरपेक्ष शब्दों का अंतर अज्ञात का मान अज्ञात का होगा।
 
<s>भास्कर द्वितीय कहते हैं:</s>
 
<s>"अज्ञात को एक तरफ से दूसरी तरफ से और दूसरी तरफ निरपेक्ष पद को पहली तरफ से घटाएं। अवशिष्ट निरपेक्ष संख्या को अज्ञात के अवशिष्ट गुणांक से विभाजित किया जाना चाहिए; इस प्रकार अज्ञात का मूल्य ज्ञात हो जाता है।</s>
 
नारायण लिखते हैं:
 
"एक तरफ से 'अज्ञात' और दूसरी तरफ से ज्ञात मात्रा को साफ़ करें, फिर अज्ञात के अवशिष्ट गुणांक द्वारा ज्ञात अवशिष्ट को विभाजित करें। इस प्रकार निश्चित रूप से अज्ञात का मूल्य ज्ञात हो जाएगा।"
 
उदाहरण के लिए हम ब्रह्मगुप्त द्वारा प्रस्तावित एक समस्या लेते हैं:
 
"उस समय के लिए बीते हुए दिनों की संख्या बताएं जब अवशिष्ट डिग्री के बारहवें भाग में एक से चार गुना वृद्धि हुई हो, जमा आठ शेष के बराबर होगा
 
डिग्री प्लस वन।"
 
इसे चतुर्वेद पृथुदका स्वामी ने इस प्रकार हल किया है:
 
"यहाँ अवशिष्ट अंश ''यावत्-तावत्''  हैं,
 
''या''  एक की वृद्धि हुई, ''या'' 1 ''रु'' 1; इसका बारहवाँ भाग, (''या'' 1 ''रु'' 1) / 12
 
इसका चार गुना, ''(या'' 1 ''रु'' 1) / 3 ; प्लस निरपेक्ष मात्रा आठ, (''या'' 1 ''रु'' 25) / 3।
 
यह अवशिष्ट डिग्री प्लस एकता के बराबर है।
 
दोनों पक्षों का बयान इस प्रकार
 
तिगुना है
 
''या''  1 ''रु'' 25
 
''या''  3 ''रु'' 3
 
अज्ञात के गुणांकों के बीच का अंतर 2 है। इससे निरपेक्ष पदों का अंतर, अर्थात् 22, विभाजित किया जा रहा है, सूर्य की डिग्री के अवशिष्ट का उत्पादन किया जाता है। 11. इन अवशिष्ट डिग्री को अलघुकरणीय के रूप में जाना चाहिए। बीते हुए दिनों को पहले की तरह (आगे बढ़ते हुए) घटाया जा सकता है।"
 
दूसरे शब्दों में, हमें समीकरण को हल करना होगा
 
<math>{\displaystyle {\frac{4}{12}(x+1)+8 = x+1}}</math>
 
जो देता है x + 25 = 3x + 3
 
2x = 22
 
इसलिए x= 11
 
निम्नलिखित समस्या और उसका समाधान भास्कर द्वितीय के बीजगणित से हैं:
 
"एक व्यक्ति के पास तीन सौ सिक्के और छह घोड़े हैं। दूसरे के पास समान मूल्य के दस घोड़े (प्रत्येक) हैं और उस पर सौ सिक्कों का और कर्ज है। लेकिन वे
 
समान मूल्य के हैं। घोड़े की कीमत क्या है?
 
"यहाँ सम-निकासी के लिए कथन है:
 
6x + 300 = 10x - 100
 
अब, नियम के अनुसार, 'एक तरफ से अज्ञात को दूसरी तरफ से घटाएं', पहली तरफ अज्ञात को दूसरी तरफ से घटाया जा रहा है,
 
शेष 4x है। दूसरी तरफ का निरपेक्ष पद पहली तरफ के निरपेक्ष पद से घटाया जाता है, तो शेष 400 होता है। शेष ज्ञात
 
संख्या 400 को अवशिष्ट अज्ञात 4x के गुणांक से विभाजित किया जा रहा है, भागफल को x, (अर्थात् 100) के मान के रूप में पहचाना जाता है।"
 
== दो अज्ञात के साथ रैखिक समीकरण ==
 
==== सहमति का नियम ====
आमतौर पर लगभग सभी हिंदू लेखकों द्वारा चर्चा का एक विषय ''सन्निपतन/संक्रमण'' (सहमति) के विशेष नाम से जाना जाता है। नारायण (1350) के अनुसार इसे ''संक्रम''  भी कहा जाता है। ब्रह्मगुप्त (628) ने इसे बीजगणित में शामिल किया है जबकि अन्य इसे अंकगणित के दायरे में आने के रूप में मानते हैं। जैसा कि समीक्षक गंगा-धार (1420) द्वारा समझाया गया है, यहां चर्चा का विषय "दो राशियों की जांच समवर्ती या उनके योग और अंतर के रूप में एक साथ उगाई गई है।"
 
दूसरे शब्दों में संक्रमण समकालिक समीकरणों का समाधान है
 
x+ y= a, x-y= b
 
समाधान के लिए ब्रह्मगुप्त का नियम है: "योग को अंतर से बढ़ाया और घटाया जाता है और दो से विभाजित किया जाता है; (परिणाम दो अज्ञात मात्रा होगी): (यह है) सहमति। उसी नियम को उनके द्वारा एक अलग अवसर पर पुन: स्थापित किया गया है समस्या का रूप और उसका समाधान।
 
"दो (स्वर्गीय पिंडों) के अवशेषों का योग और अंतर डिग्री और मिनटों में जाना जाता है। अवशेष क्या हैं? अंतर को योग से जोड़ा और घटाया जाता है, और आधा किया जाता है; (परिणाम हैं) अवशेष।
 
==== रेखीय समीकरण ====
महावीर निम्नलिखित उदाहरण देते हैं जो प्रत्येक के समाधान के नियमों के साथ-साथ एक साथ रैखिक समीकरण बनाते हैं।
 
उदाहरण। "9 सिट्रन और 7 सुगंधित लकड़ी-सेब की एक साथ कीमत 107 है, फिर से 7 साइट्रॉन और 9 सुगंधित लकड़ी-सेब की कीमत एक साथ ली गई है
 
101 है। हे गणितज्ञ, मुझे जल्दी से एक साइट्रोन और एक सुगंधित लकड़ी-सेब की कीमत अलग-अलग बताओ।"
 
यदि x, y क्रमशः एक साइट्रोन और एक सुगंधित लकड़ी-सेब की कीमतें हों, तो
 
9x+7y= 107,
 
7x+9y = 101.
 
या, सामान्य तौर पर,
 
ax+ by = m
 
bx + ay = n
 
समाधान। "बड़ी मात्रा में (संबंधित) चीजों की बड़ी संख्या से गुणा की गई बड़ी संख्या में चीजों की संख्या के वर्गों के अंतर से विभाजित (संबंधित) छोटी संख्या से गुणा की गई कीमत की छोटी राशि घटाएं। (शेष) चीजों की संख्या के वर्गों के अंतर से विभाजित बड़ी संख्या में प्रत्येक वस्तु की कीमत होगी दूसरे की कीमत गुणक को उलटने से प्राप्त होगी।
 
इस प्रकार  <math>{\displaystyle x = {\frac{(am - bn)}{(a^2 -b^2)}} }</math> , <math>{\displaystyle y = {\frac{(an - bm)}{(a^2 -b^2)}} }</math>
 
इसके समाधान के साथ निम्नलिखित उदाहरण भास्कर द्वितीय के बीजगणित से लिया गया है:
 
उदाहरण। "एक कहता है, 'मुझे सौ दो, मित्र, तब मैं तुमसे दुगना धनवान बन जाऊँगा।' दूसरा जवाब देता है, 'यदि आप मुझे दस देते हैं, तो मैं छह गुना अमीर हो जाऊंगा  जैसे आप।' मुझे बताओ कि उनकी (संबंधित) राजधानियों की राशि क्या है?"
 
समीकरण हैं
 
x + 100 = 2(y - 100) (I)
 
y + 10 = 6(x - 10)    (2)
 
भास्कर  द्वितीय इन समीकरणों को हल करने के दो तरीकों को इंगित करता है। वे काफी हद तक इस प्रकार हैं:
 
'''पहली विधि:'''
 
मान लीजिए x = 2z - 100, y = z + 100,
 
ताकि समीकरण (I) समान रूप से संतुष्ट हो। स्थानापन्न
 
दूसरे समीकरण में ये मान, हम प्राप्त करते हैं
 
z + 110 = 12z- 660;
 
इसलिये z =70 , जिसकी  वजह  से - x = 40 , y = 170
 
'''दूसरी विधि:'''
 
समीकरण (I) से, हम प्राप्त करते हैं
 
x =2y - 300,
 
और समीकरण (2) से
 
<math>{\displaystyle x = {\frac{1}{6}}(y+70) }</math>
 
x के इन दो मानों की बराबरी करने पर हमें प्राप्त होता है
 
<math>{\displaystyle 2y -300 = {\frac{1}{6}}(y+70) }</math>
 
<math>{\displaystyle 12y -1800 = y+70 }</math>
 
अत: y= 170. y के इस मान को x के दो व्यंजकों में से किसी में प्रतिस्थापित करने पर, हमें x = 40 प्राप्त होता है।
 
== कई अज्ञात के साथ रैखिक समीकरण ==
 
==== रैखिक समीकरणों का एक प्रकार ====
कई अज्ञातों को शामिल करने वाले रैखिक समीकरणों की प्रणालियों का सबसे पहला हिंदू उपचार बख्शाली ग्रंथ में पाया जाता है। इसमें एक समस्या इस प्रकार है:
 
"[तीन व्यक्तियों में प्रत्येक के पास एक निश्चित मात्रा में धन होता है।] पहले और दूसरे के धन को मिलाकर 13 की राशि; दूसरे की संपत्ति और
 
एक साथ लिया गया तीसरा 14 है; और पहिले और तीसरे मिले जुले लोगों की दौलत 15 मानी गई है।
 
यदि x1, x2, x3 क्रमशः तीन व्यापारियों की संपत्ति हो, तो x1 + x2 = 13, x2 + x3 = 14, x3 + x1 = 15.
 
एक और समस्या यह है कि "पांच व्यक्तियों के पास एक निश्चित मात्रा में धन होता है। पहले और दूसरे के धन को मिलाकर 16 की राशि मिलती है; दूसरे और तीसरे के धन को मिलाकर 17 माना जाता है; तीसरे का धन और चौथे को मिलाकर 18 माना जाता है; चौथे और पांचवें को मिलाकर धन 19 है; और पहले और पांचवें का धन मिलाकर 20 है। मुझे बताओ कि प्रत्येक की राशि क्या है  x₁ x₂ x₃ x₄ x₅
 
x₁ + x₂ = 16, x₂ + x₃ = 17, x₃+ x₄ = 18, x₄ + x₅ = 19, x₅ + x₁ = 20
 
काम में इसी तरह की कुछ और समस्याएं हैं। उनमें से हर एक प्रकार के रैखिक समीकरणों की एक प्रणाली से संबंधित है
 
x₁ + x₂ = a1, x₂ + x₃ = a2 ..., xn + x₁ = an, n विषम होना।
 
==== असत्य स्थिति से समाधान ====
इस प्रकार के रैखिक समीकरणों की एक प्रणाली बख्शाली ग्रंथ में निम्नानुसार हल की गई है:
 
x₁ के लिए एक मनमाना मान p मान लें और फिर उसके संगत x₂, x₃, ... के मानों की गणना करें। अंत में x<sub>n</sub> + x₁ का परिकलित मान b के बराबर होने दें
 
(कहो)।  तब x₁ का सही मान सूत्र द्वारा प्राप्त किया जाता है
 
<math>{\displaystyle x_1 = p +{\frac{1}{2}}(a_n- b)}</math>
 
विशेष मामले में (1) लेखक x के लिए मनमाना मान 5 मानता है; फिर क्रमशः x₂ = 8, x₃ = 6 और x₃ + x₁ = 11 के मानों की गणना की जाती है
 
इसलिए सही मान हैं,
 
x₁= 5 + (15 - 11)/2 = 7, x₂ = 6, x₃= 8
 
तर्क। उन्मूलन की प्रक्रिया से हम प्राप्त करते हैं
 
समीकरण (I)
 
(a<sub>2</sub>-a<sub>1</sub>)+(a<sub>4</sub>-a<sub>3</sub>)+· ... +(a<sub>n-1</sub> - a<sub>n-2</sub>) + 2x<sub>1</sub> = a<sub>n</sub>
 
मान लें x<sub>1</sub> = p; ताकि
 
(a<sub>2</sub>-a<sub>1</sub>)+(a<sub>4</sub>-a<sub>3</sub>)+· ... +(a<sub>n-1</sub> - a<sub>n-2</sub>) + 2p = b कहें।
 
घटाना 2(x<sub>1</sub> - p) = a - b
 
अतः  <math>{\displaystyle x_1 =p + {\frac{1}{2}}(a_n-b) }</math>
 
==== दूसरा प्रकार ====
समीकरणों के प्रकार (I) का एक विशेष मामला जिसके लिए n = 3, को भी रैखिक समीकरणों के एक अलग प्रकार के प्रणाली से संबंधित माना जा सकता है।
 
Σx - x<sub>1</sub> = a<sub>1</sub> , Σx - x<sub>2</sub> = a<sub>2</sub>, Σx - x<sub>n</sub> = a<sub>n</sub>
 
जहाँ Σx का अर्थ है x<sub>1</sub> + x<sub>2</sub> +....+x<sub>n</sub>
 
लेकिन इसके समीकरणों को कहना ठीक नहीं होगा। प्रकार का व्यवहार बख्शिली ग्रंथ में किया गया है। l हालाँकि, आर्यभट्ट (499) और महावीर (850) द्वारा उन्हें हल किया गया है। पहला कहता है: "कुछ (अज्ञात) संख्याओं के (दिए गए) योग, एक क्रम में एक संख्या को छोड़कर, अलग-अलग जोड़े जाते हैं और कम से कम पदों की संख्या से विभाजित होते हैं; वह (भागफल) पूरे का मूल्य होगा।
 
<math>{\displaystyle \sum x = \sum_{r=1}^n a_r/(n-1) }</math>
 
महावीर समाधान इस प्रकार बताते हैं: "एक साथ जोड़ी गई वस्तुओं की बताई गई मात्रा को पुरुषों की संख्या से कम से विभाजित किया जाना चाहिए। भागफल कुल मूल्य (सभी वस्तुओं का) होगा। प्रत्येक बताई गई राशि को उसमें से घटाया जा रहा है, (मूल्य) हाथों में (प्रत्येक का मिल जाएगा)।
 
अपना शासन बनाने में महावीर ने निम्नलिखित उदाहरण को ध्यान में रखा था:
 
"चार व्यापारियों से प्रत्येक को सीमा शुल्क अधिकारी द्वारा उनकी वस्तुओं के कुल मूल्य के बारे में अलग से पूछा गया था।
 
पहले व्यापारी ने अपने स्वयं के निवेश को छोड़कर, इसे 22 बताया; दूसरे ने इसे 23, तीसरे 24 और चौथे 27 को बताया; उनमें से प्रत्येक काटा गया
 
निवेश में अपनी राशि। हे मित्र, प्रत्येक के स्वामित्व वाली वस्तु का (हिस्सा) मूल्य अलग से बताओ।"
 
यहाँ <math>{\displaystyle x_1 + x_2+x_3+x_4 = {\frac{22+23+24+27}{4-1}}=32}</math>
 
इसलिए x<sub>1</sub> = 10, x<sub>2</sub> = 9, x<sub>3</sub> = 8, x<sub>4</sub> = 5.
 
नारायण कहते हैं: "एक से कम व्यक्तियों की संख्या से विभाजित राशि का योग, कुल राशि है। इसमें से बताई गई राशियों को अलग-अलग घटाने पर अलग-अलग राशियाँ मिलेंगी।"
 
==== तीसरा प्रकार ====
रैखिक समीकरणों की एक अधिक सामान्यीकृत प्रणाली होगी
 
<math>{\displaystyle b_1\sum x - c_1x_1=a_1 }</math> , <math>b_2\sum x - c_2x_2=a_2</math> ......,
 
<math>b_n\sum x - c_nx_n=a_n</math> ..........................................(III)
 
इसलिए  <math>{\displaystyle  \sum x  =  {\frac { \sum (a/c)}{ \sum(b/c) -1}}}</math>
 
अतः  <math>{\displaystyle  x_r ={\frac{b_r}{c_r}}  . {\frac { \sum (a/c)}{ \sum(b/c) -1}} - {\frac{a_r}{c_r}}}</math>....................(I)
 
r = I, 2, 3..... n
 
इस प्रकार का एक विशेष मामला महावीर के निम्नलिखित उदाहरण द्वारा प्रस्तुत किया गया है:
 
"तीन व्यापारी आपस में एक-दूसरे से भीख माँगते थे। पहला दूसरे से 4 और तीसरे से 5 भीख माँगने पर दूसरे की तुलना में दुगना धनी हो गया। दूसरा पहले से 4 और तीसरे से 6 होने पर तीन गुना धनी हो गया। तीसरा आदमी भीख मांगने पर पहले से 5 और दूसरे से 6 गुना अमीर बन गया।हे गणितज्ञ, यदि आप चित्रा-कुट्टक-मिश्रा जानते हैं, तो मुझे जल्दी से बताओ कि प्रत्येक के हाथ में कितनी राशि थी। "
 
यानी हमें समीकरण मिलते हैं
 
x + 4 + 5 = 2(y + z - 4 - 5),
 
y + 4 + 6 = 3(z + x - 4 - 6),
 
z + 5 + 6 = 5 (x + y - 5 - 6);
 
or 2(x + y + z) - 3x = 27,
 
3(x + y + z) - 4y = 40 ;
 
5 (x + y +z) - 6z = 66;
 
प्रणाली का एक विशेष मामला (III) में प्रतिस्थापन
 
(I), हम पाते हैं
 
x = 7,  Y = 8, Z = 9
 
'''ब्रह्मगुप्त का नियम''': ब्रह्मगुप्त (628) कई अज्ञात से जुड़े रैखिक समीकरणों को हल करने के लिए निम्नलिखित नियम बताता है:
 
"पहले अज्ञात की तरफ से अन्य अज्ञात को हटाकर और पहले अज्ञात के गुणांक से विभाजित करके, पहले अज्ञात का मान प्राप्त किया जाता है। पहले अज्ञात के अधिक मूल्यों के मामले में, दो और दो (उनमें से) चाहिए उन्हें आम भाजक में कम करने के बाद विचार किया जाना चाहिए। और इसी तरह बार-बार। यदि अंतिम समीकरण में और अधिक अज्ञात रहते हैं, तो पल्वराइज़र की विधि को नियोजित किया जाना चाहिए। फिर विपरीत तरीके से आगे बढ़ने पर अन्य अज्ञात के मान पाए जा सकते हैं।"
 
चतुर्वेद पृथुदका स्वामी  (860) ने इसे इस प्रकार समझाया है: "एक ऐसे उदाहरण में जिसमें दो या अधिक अज्ञात मात्राएँ हों, यवत-तवत, आदि जैसे रंगों को उनके मूल्यों के लिए मान लिया जाना चाहिए। उन पर सभी कार्यों को अनुरूप रूप से किया जाना चाहिए। उदाहरण के बयान और इस प्रकार दो या दो से अधिक पक्षों और समीकरणों को भी ध्यान से तैयार किया जाना चाहिए। समानता-निकासी पहले दो और दो के बीच की जानी चाहिए और इसी तरह अंतिम तक: एक तरफ से एक अज्ञात को साफ किया जाना चाहिए, अन्य अज्ञात को कम किया जाना चाहिए एक आम भाजक के लिए और साथ ही निरपेक्ष संख्या को विपरीत पक्ष से साफ किया जाना चाहिए। अन्य अज्ञात के अवशेषों को पहले अज्ञात के अवशिष्ट गुणांक से विभाजित किया जा रहा है, पहले अज्ञात का मान देगा। यदि ऐसे कई मान प्राप्त होते हैं, तो उनमें से दो और दो के साथ, सामान्य भाजक को घटाकर समीकरण बनाए जाने चाहिए। इस तरह से अंत तक आगे बढ़ते हुए एक अज्ञात का मान ज्ञात करें। यदि वह मान किसी अन्य अज्ञात के संदर्भ में हो तो गुणांक उन दोनों के सायंट परस्पर दो अज्ञातों के मान होंगे। यदि, हालांकि, उस मूल्य में और अधिक अज्ञात मौजूद हैं, तो पल्वराइज़र (चूर्णित) की विधि को नियोजित किया जाना चाहिए। कुछ अज्ञातों के लिए मनमाना मूल्य तब माना जा सकता है।" यह ध्यान दिया जाएगा कि उपरोक्त नियम अनिश्चित के साथ-साथ निर्धारित समीकरणों को भी शामिल करता है। वास्तव में, नियम के चित्रण में ब्रह्मगुप्त द्वारा दिए गए सभी उदाहरण अनिश्चित चरित्र के हैं। हम उनमें से कुछ का उल्लेख बाद में उनके उचित स्थानों पर करेंगे। जहाँ तक एक साथ निर्धारित समीकरणों का संबंध है, उन्हें हल करने के लिए ब्रह्मगुप्त की विधि आसानी से हमारे वर्तमान के समान ही मानी जाएगी।
 
'''भास्कर का नियम:''' भास्कर द्वितीय ने व्यावहारिक रूप से ब्रह्मगुप्त के समान ही नियम दिया है, जिसमें कई अज्ञात को शामिल करते हुए एक साथ रैखिक समीकरणों को हल किया जाता है।
 
हम उनके कार्यों से निम्नलिखित दृष्टांत लेते हैं।
 
उदाहरण 1. "आठ माणिक, दस पन्ने और सौ मोती जो तेरे कान की अंगूठी में हैं, मेरे द्वारा आपके लिए समान मात्रा में खरीदे गए थे; तीन प्रकार के रत्नों की कीमत दरों का योग आधे से तीन कम है सौ का। मुझे बताओ, 0 प्रिय शुभ महिला, यदि आप गणित में कुशल हैं, तो प्रत्येक की कीमत।"
 
यदि x, y, z क्रमशः माणिक, पन्ना और मोती की कीमतें हों, तो 8x = 10y = 100z
 
x+y+z = 47
 
भास्कर II कहते हैं, समान राशि को w मान लें, तो हम प्राप्त करेंगे
 
x = w/8, y = w/10, z = w/100
 
शेष समीकरण में प्रतिस्थापित करने पर, हम आसानी से w = 200 प्राप्त करते हैं। इसलिए
 
x = 25, y = 20, z = 2
 
== द्विघातीय समीकरण ==
सरल द्विघात समीकरण का ज्यामितीय हल[[File:Quadratic equation.gif|alt=समीकरण|thumb|समीकरण ]]
 
<math>4h^2 -4dh =- c^2</math>  जैनों (500- 300 ईसा पूर्व) के प्रारंभिक विहित कार्यों में और उमास्वती (सी। 150 ई.पू.) के ''तत्त्वाधिगमा-सूत्र''  में भी पाया जाता है।
 
<math>{\displaystyle h = {\frac {1}{2}} (d-\sqrt{d^2-c^2})}</math>
 
'''श्रीधर का शासन:'''  श्रीधर (सी। 750) द्विघात समीकरण को हल करने की अपनी विधि को स्पष्ट रूप से इंगित करता है।
 
बीजगणित पर उनका ग्रंथ अब खो गया है। लेकिन इसका प्रासंगिक हिस्सा भास्कर द्वितीय और अन्य के उद्धरणों में संरक्षित है। श्रीधर की विधि है: ।
 
"दोनों पक्षों (एक समीकरण के) को अज्ञात के वर्ग के गुणांक के चार गुणा के बराबर ज्ञात मात्रा से गुणा करें; दोनों पक्षों में एक ज्ञात जोड़ें
 
अज्ञात के (मूल) गुणांक के वर्ग के बराबर मात्रा: फिर मूल निकालें।"
 
अर्थात् <math>ax^2 + bx = c</math>  को हल करने के लिए,
 
दोनों पक्षों में 4a से गुणा करें
 
हमारे पास है  <math>4a^2x^2 + 4abx = 4ac</math>
 
या
 
<math>(2ax+b)^2 = 4ac + b^2</math>
 
<math>2ax+b = \sqrt{4ac + b^2}</math>
 
<math>x= \frac{\sqrt{4ac+b^2} -b}{2a}</math>
 
'''श्रीपति के नियम:'''  श्रीपति (1039) द्विघात को हल करने की दो विधियों को इंगित करता है। पहली विधि का वर्णन करने वाले नियम में हमारी पांडुलिपि में एक कमी/अंतर है, लेकिन इसे आसानी से श्रीधर के समान माना जा सकता है। "अज्ञात के वर्ग के गुणांक से चार गुना गुणा करें और अज्ञात के गुणांक के वर्ग को जोड़ें; फिर अज्ञात के वर्ग के गुणांक के दोगुने से विभाजित वर्गमूल निकालें, का मान कहा जाता है अनजान।" "या अज्ञात के वर्ग के गुणांक से गुणा करके और अज्ञात के गुणांक के आधे के वर्ग को जोड़कर, वर्गमूल निकालें। फिर पहले की तरह आगे बढ़ते हुए, यह अज्ञात के गुणांक के आधे से कम हो जाता है और गुणांक से विभाजित हो जाता है। अज्ञात के वर्ग का। इस भागफल को अज्ञात का मान कहा जाता है।"
 
<math>ax^2 + bx = c</math>
 
or <math>{\displaystyle a^2x^2+ abx  +\left ( \frac{b}{2} \right )^2 =  ac +\left ( \frac{b}{2} \right )^2 }</math>
 
इसलिए  <math>{\displaystyle ax+ \left ( \frac{b}{2} \right ) = \sqrt{ac + \left ( \frac{b}{2} \right ) ^2} }</math>
 
<math>{\displaystyle x=  \frac{\sqrt{ac + \left ( \frac{b}{2} \right ) ^2} - \frac{b}{2}}{a}  }
</math>
</math>
अद्वितीय समाधान x= −1, y=1 है।


'''भास्कर द्वितीय के नियम :'''  भास्कर द्वितीय (1150) कहते  हैं : "जब अज्ञात का वर्ग, आदि रहता है, तो दोनों पक्षों (समीकरण के) को कुछ उपयुक्त मात्राओं से गुणा करके, अन्य उपयुक्त मात्राओं को जोड़ा जाना चाहिए ताकि पक्ष युक्त अज्ञात एक मूल (''पद-प्रद)'' उत्पन्न करने में सक्षम हो जाता है। फिर समीकरण को इस पक्ष की जड़ और ज्ञात पक्ष की जड़ के साथ फिर से बनाया जाना चाहिए। इस प्रकार अज्ञात का मूल्य उस समीकरण से प्राप्त होता है।
=== सर्वसमिका ===
 
इस नियम को लेखक ने आगे इस प्रकार स्पष्ट किया है : .
 
"जब दोनों पक्षों की पूर्ण निकासी के बाद, एक तरफ अज्ञात का वर्ग, आदि रहता है और दूसरी तरफ केवल पूर्ण शब्द होता है, तो, दोनों पक्षों को कुछ उपयुक्त वैकल्पिक मात्रा से गुणा या विभाजित किया जाना चाहिए; कुछ समान मात्राओं को आगे दोनों पक्षों से जोड़ा या घटाया जाना चाहिए ताकि अज्ञात पक्ष एक जड़ पैदा करने में सक्षम हो जाए। उस पक्ष की जड़ दूसरी तरफ के निरपेक्ष पदों के मूल के बराबर होनी चाहिए। के लिए, द्वारा एक साथ समान जोड़, आदि, दो समान पक्षों के लिए समानता बनी हुई है। इसलिए इन जड़ों के साथ फिर से एक समीकरण बनाने से अज्ञात का मान मिल जाता है।"
 
यह ध्यान दिया जा सकता है कि भास्कर द्वितीय के अंकगणित पर अपने ग्रंथ में हमेशा अज्ञात के वर्ग के गुणांक द्वारा विभाजित करने की आधुनिक पद्धति का पालन किया गया है।
 
ज्ञानराज (1503) और गणेश (1545) द्विघात को हल करने के लिए भास्कर द्वितीय के समान सामान्य तरीकों का वर्णन करते हैं।
 
'''मध्य अवधि का उन्मूलन :'''द्विघात को हल करने की विधि हिंदू बीजगणितविदों के बीच तकनीकी पदनाम ''मध्यमहारना''  या "मध्य का उन्मूलन" (''मध्यम'' = मध्य और ''अहारना'' = हटाने, या नष्ट करने, यानी उन्मूलन) से जानी जाती थी। विधि के अंतर्निहित सिद्धांत में नाम की उत्पत्ति आसानी से मिल जाएगी। इसके द्वारा एक द्विघात समीकरण, जिसके सामान्य रूप में, तीन पद होते हैं और इसलिए एक मध्य पद होता है, एक शुद्ध द्विघात समीकरण या एक साधारण समीकरण में कम हो जाता है जिसमें केवल दो पद होते हैं और इसलिए कोई मध्य पद नहीं होता है। इस प्रकार मूल द्विघात के मध्य पद को इसके समाधान के लिए सामान्यतः अपनाई गई विधि द्वारा समाप्त कर दिया जाता है। और इसलिए नाम भास्कर द्वितीय ने देखा है, "यह भी विशेष रूप से विद्वान शिक्षकों द्वारा ''मध्यमहारना''  के रूप में नामित किया गया है। इसके द्वारा, द्विघात के दो शब्दों में से एक को हटा दिया जाता है, मध्य एक, होता है।" हालाँकि, नाम को एक विस्तारित अर्थ में भी नियोजित किया जाता है ताकि घन और द्विघात को हल करने के तरीकों को अपनाया जा सके, जहाँ कुछ शर्तों को भी समाप्त कर दिया जाता है। यह ब्रह्मगुप्त (628) के कार्यों के रूप में जल्दी होता है।


'''द्विघात की दो जड़ें :''' हिंदुओं ने जल्दी ही पहचान लिया कि द्विघात के मूल रूप से दो मूल होते हैं। इस संबंध में भास्कर द्वितीय ने पद्मनाभ नाम के एक प्राचीन लेखक से निम्नलिखित नियम उद्धृत किया है जिसका बीजगणित पर ग्रंथ अब उपलब्ध नहीं है। "यदि मूलों को निकालने के बाद द्विघात की निरपेक्ष भुजा का वर्गमूल दूसरी ओर के ऋणात्मक निरपेक्ष पद से कम हो, तो इसे ऋणात्मक और धनात्मक लेने पर अज्ञात के दो मान मिलते हैं।"
{{main|सर्वसमिका (गणित)|त्रिकोणमितीय सर्वसमिकाओं की सूची}}


भास्कर कुछ विशिष्ट दृष्टांतों की मदद से बताते हैं कि हालांकि द्विघात की ये दोहरी जड़ें सैद्धांतिक रूप से सही हैं, वे कभी-कभी असंगति की ओर ले जाती हैं और इसलिए हमेशा स्वीकार नहीं किया जाना चाहिए। इसलिए वह नियम को इस प्रकार संशोधित करता है: "यदि द्विघात के ज्ञात पक्ष का वर्गमूल अज्ञात पक्ष के वर्गमूल में होने वाले ऋणात्मक निरपेक्ष पद से कम हो, तो इसे ऋणात्मक और सकारात्मक बनाते हुए, दो मान अज्ञात का निर्धारण किया जाना चाहिए। यह कभी-कभी किया जाना चाहिए।"
एक सर्वसमिका एक समीकरण है जो इसमें निहित चर(नों) के सभी संभावित मानों के लिए सत्य है। बीजगणित और कलन में अनेक सर्वसमिकाएँ ज्ञात हैं। एक समीकरण को हल करने की प्रक्रिया में, एक समीकरण को सरल बनाने के लिए प्रायः एक सर्वसमिका का उपयोग किया जाता है, जिससे इसे अधिक आसानी से हल किया जा सकता है।


उदाहरण 1. "चौकोर बंदरों की एक टुकड़ी का आठवां हिस्सा, खुशी-खुशी उससे जुड़कर, जंगल के अंदर कूद रहा था। बारह पहाड़ी पर चिल्लाते और चिल्लाते हुए खुश थे। वे कितने थे?"
बीजगणित में, एक सर्वसमिका का उदाहरण [[दो वर्गों का अंतर]] है:


समाधान। "यहाँ बंदरों का दल x है। इसके आठवें भाग का वर्ग 12 को मिलाकर सेना के बराबर है। तो दोनों भुजाएँ हैं
:<math>x^2 - y^2 = (x+y)(x-y) </math>
जो सभी x और y के लिए सत्य है।


<math>{\displaystyle  {\frac{1}{64}}x^2+0x+12 = 0x^2+x+0}</math>
[[त्रिकोणमिति]] एक ऐसा क्षेत्र है जहां कई सर्वसमिका मौजूद हैं; ये [[त्रिकोणमितीय समीकरण|त्रिकोणमितीय समीकरणों]] में हेरफेर करने या हल करने में उपयोगी होते हैं। कई में से दो जिनमें [[साइन समारोह|द्विज्या]] और [[कोसाइन समारोह|कोटिज्या]] प्रकार्य सम्मिलित हैं:


इन्हें एक सामान्य भाजक में कम करना और फिर हर को हटाना, और निकासी करना भी दोनों पक्ष बन जाते हैं
:<math>\sin^2(\theta)+\cos^2(\theta) = 1 </math>
और


x² - 64x + 0 = 0x2 + 0x - 768
:<math>\sin(2\theta)=2\sin(\theta) \cos(\theta) </math>
जो θ के सभी मानों के लिए सत्य हैं।


दोनों पक्षों में 32 का वर्ग जोड़ने पर और वर्गमूल निकालने पर, हमें प्राप्त होता है
उदाहरण के लिए, समीकरण को संतुष्ट करने वाले θ के मान को हल करने के लिए:


x- 32 = ± (0x + 16)
:<math>3\sin(\theta) \cos(\theta)= 1\,, </math>
जहां θ 0 और 45 डिग्री के बीच सीमित है, कोई उत्पाद देने के लिए उपरोक्त सर्वसमिका का उपयोग कर सकता है:


इस उदाहरण में ज्ञात पक्ष पर निरपेक्ष पद अज्ञात के पक्ष में ऋणात्मक निरपेक्ष पद से छोटा है; इसलिए इसे सकारात्मक के साथ-साथ नकारात्मक भी लिया जाता है; x के दो मान 48, 16 पाए जाते हैं।
:<math>\frac{3}{2}\sin(2 \theta) = 1\,,</math>
θ के लिए निम्नलिखित समाधान प्राप्त करना:


== उच्च डिग्री के समीकरण ==
:<math>\theta = \frac{1}{2} \arcsin\left(\frac{2}{3}\right) \approx 20.9^\circ.</math>
'''घन और द्विघात:''' हिंदुओं ने घन और द्विघात समीकरणों के समाधान में बहुत कुछ हासिल नहीं किया। भास्कर द्वितीय (1150) ने ''मध्यमहारना'' (मध्य का उन्मूलन) की विधि को उन समीकरणों पर भी लागू करने का प्रयास किया ताकि लाभप्रद परिवर्तनों के माध्यम से उन्हें कम किया जा सके और क्रमशः सरल और द्विघात समीकरणों के लिए सहायक मात्राओं का परिचय दिया जा सके। इस प्रकार उन्होंने द्विघात को हल करने के आधुनिक तरीकों में से एक का अनुमान लगाया। "यदि, हालांकि," भास्कर द्वितीय का कहना है, "घन, द्विघात, आदि की उपस्थिति के कारण, अज्ञात पक्ष की जड़ के अभाव में, इस तरह के संचालन के प्रदर्शन के बाद, कमी का कार्य आगे नहीं बढ़ सकता है ( एक समीकरण का), तो अज्ञात का मान सरलता (गणितज्ञ के) द्वारा प्राप्त किया जाना चाहिए।" उन्होंने दो उदाहरण दिए हैं, एक घन का और दूसरा द्विघात का, जिसमें ऐसी कमी संभव है।
चूँकि ज्या फलन एक आवर्ती फलन है, यदि θ पर कोई प्रतिबंध नहीं है तो इसके अपरिमित रूप से अनेक समाधान हैं। इस उदाहरण में, θ को 0 और 45 डिग्री के बीच सीमित करने से समाधान केवल एक संख्या तक सीमित हो जाएगा।


उदाहरण 1. "वह कौन सी संख्या है, जिसे बारह से गुणा करने पर और संख्या के घन से बढ़ाने पर पैंतीस के साथ जोड़ी गई संख्या के वर्ग के छह गुणा के बराबर होती है।
== गुण ==


समाधान। "यहाँ संख्या x है। इसे बारह से गुणा किया जाता है और संख्या के घन से बढ़ाकर x³ + 12x हो जाता है। यह 6x² + 35 के बराबर होता है। निकासी करने पर, पहली तरफ x³ - 6x² + 12x; पर दिखाई देता है। दूसरा पक्ष 35. दोनों पक्षों में ऋणात्मक आठ जोड़ने पर और घनमूल निकालने पर हमें x - 2. = 0x + 3 प्राप्त होता है और इस समीकरण से संख्या 5 मिलती है।
दो समीकरण या समीकरणों की दो प्रणालियाँ समतुल्य होती हैं, यदि उनके हलों का एक ही समुच्चय हो। निम्नलिखित संक्रियाएँ एक समीकरण या समीकरणों की एक प्रणाली को एक समतुल्य में बदल देती हैं - बशर्ते कि संक्रियाएँ उन व्यंजकों के लिए सार्थक हों जिन पर वे लागू होते हैं:
* किसी समीकरण के दोनों पक्षों में समान मात्रा को जोड़ना या घटाना। इससे पता चलता है कि प्रत्येक समीकरण उस समीकरण के तुल्य होता है जिसमें दाहिनी ओर शून्य होता है।
* एक समीकरण के दोनों पक्षों को एक गैर-शून्य मात्रा से गुणा या विभाजित करना।
* समीकरण के एक पक्ष को बदलने के लिए एक सर्वसमिका (गणित) लागू करना। उदाहरण के लिए, [[बहुपद विस्तार]] एक उत्पाद या बहुपदों का गुणन [[योग|योग है]]।
* एक प्रणाली के लिए एक समीकरण के दोनों पक्षों में दूसरे समीकरण के संबंधित पक्ष को जोड़कर, समान मात्रा से [[गुणा]] किया जाता है।


उदाहरण 2. "वह कौन सी संख्या है जिसे 200 से गुणा करके संख्या के वर्ग में जोड़ा जाता है, और फिर 2 से गुणा किया जाता है और संख्या की चौथी शक्ति से घटाया जाता है, तो वह असंख्य कम एकता बन जाएगी? वह संख्या बताएं।
यदि किसी समीकरण के दोनों पक्षों पर कुछ प्रकार्य (गणित) लागू किया जाता है, तो परिणामी समीकरण में इसके समाधानों के बीच प्रारंभिक समीकरण के समाधान होते हैं, लेकिन इसके अतिरिक्त समाधान हो सकते हैं जिन्हें [[बाहरी समाधान]] कहा जाता है। उदाहरण के लिए, समीकरण <math>x=1</math> का समाधान है <math>x=1</math>। दोनों पक्षों को 2 के घातांक तक उठाना (जिसका अर्थ है प्रकार्य को लागू करना <math>f(s)=s^2</math> समीकरण के दोनों ओर) <math>x^2=1</math> समीकरण को बदल देता है , जिसमें न केवल पिछला समाधान है बल्कि बाहरी समाधान <math>x=-1</math> को भी प्रस्तुत करता है, इसके अलावा, यदि प्रकार्य कुछ मानों (जैसे 1/x, जो x = 0 के लिए परिभाषित नहीं है) पर परिभाषित नहीं है, तो उन मानों पर मौजूद समाधान खो सकते हैं। इस प्रकार, इस तरह के परिवर्तन को समीकरण में लागू करते समय सावधानी बरतनी चाहिए।


समाधान। "यहाँ संख्या x है; 200 से गुणा करने पर यह 200x हो जाता है; संख्या के वर्ग में जोड़ने पर x² + 200x हो जाता है; इसे दो से गुणा करने पर, 2x² + 400x; इससे संख्या की चौथी शक्ति कम हो जाती है, अर्थात्, यह x<sup>4</sup> , x<sup>4</sup>- 2x² - 400x हो जाता है। यह असंख्य कम एकता के बराबर है। समानता बनाए जाने के बाद, दोनों पक्ष होंगे,
उपरोक्त परिवर्तन समीकरण हल करने के लिए सबसे प्राथमिक तरीकों का, साथ ही कुछ कम प्राथमिक, जैसे गॉसियन उन्मूलन आधार है।


x<sup>4</sup>- 2x² - 400x = 0x<sup>4</sup> + 0x² + 0x + 9999
== बीजगणित ==


यहाँ पर पहली भुजा में चार सौ x जमा एकता जोड़ने पर जड़ निकाली जा सकती है, लेकिन दूसरी भुजा में समान जोड़ने पर उसकी जड़ नहीं बनेगी। इस प्रकार कार्य (कमी का) आगे नहीं बढ़ता है। इसलिए यहाँ, सरलता (के लिए कहा जाता है)। यहाँ दोनों पक्षों को x के वर्ग के चार गुणा, चार सौ x और एकता में जोड़ने पर और फिर मूल निकालने पर, हम प्राप्त करते हैं
=== बहुपद समीकरण ===
{{main|बहुपद समीकरण}}


x² + 0x+ 1 = 0x² + 2x + 100।
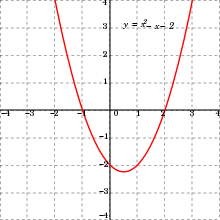
[[File:Polynomialdeg2.svg|thumb|right|220px|बहुपद समीकरण {{nowrap|1=''x''<sup>2</sup> – ''x'' + 2 = 0}} के समाधान -1 और 2 वे बिंदु हैं जहाँ द्विघात  फलन {{nowrap|1=''y'' = ''x''<sup>2</sup> – ''x'' + 2}} का लेखाचित्र x-अक्ष को काटता है।]]सामान्य तौर पर, एक बीजगणितीय समीकरण या बहुपद समीकरण रूप का एक समीकरण है


फिर से इनके साथ समीकरण बनाकर और पहले की तरह आगे बढ़ते हुए, x का मान 11 के रूप में प्राप्त होता है इसी तरह के उदाहरणों में अज्ञात का मान निर्धारित किया जाना चाहिए
:<math>P = 0</math>, या


गणितज्ञ की सरलता से।"
:<math>P = Q</math> {{efn|As such an equation can be rewritten {{math|1=''P'' – ''Q'' = 0}}, many authors do not consider this case explicitly.}}
जहाँ P और Q किसी [[क्षेत्र (गणित)|बीजीय (गणित)]] में गुणांक वाले बहुपद हैं (जैसे, परिमेय संख्या, [[वास्तविक संख्या]], सम्मिश्र संख्या)। एक बीजगणितीय समीकरण एक चर है यदि इसमें केवल एक चर (गणित) सम्मिलित है। दूसरी ओर, एक बहुपद समीकरण में कई चर सम्मिलित हो सकते हैं, जिस स्थिति में इसे बहुभिन्नरूपी (एकाधिक चर, x, y, z, आदि) कहा जाता है।


== समकालिक द्विघात समीकरण ==
उदाहरण के लिए,
'''सामान्य रूप'''  निम्नलिखित रूपों के एक साथ द्विघात समीकरणों से संबंधित विभिन्न समस्याओं का इलाज हिंदू लेखकों द्वारा किया गया है:
:<math>x^5-3x+1=0</math>
पूर्णांक गुणांक और के साथ एक अविभाज्य बीजगणितीय (बहुपद) समीकरण है
:<math>y^4+\frac{xy}{2}=\frac{x^3}{3}-xy^2+y^2-\frac{1}{7}</math>
परिमेय संख्याओं पर एक बहुभिन्नरूपी बहुपद समीकरण है।


x - y = d ; xy = b ......(1)
परिमेय संख्या वाले कुछ बहुपद समीकरणों का एक हल होता है जो एक बीजगणितीय व्यंजक होता है, जिसमें केवल उन गुणांकों को सम्मिलित करने वाली संक्रियाओं की परिमित संख्या होती है (अर्थात, बीजगणितीय हल हो सकता है)। यह बहुपद एक, दो, तीन या चार की घात के ऐसे सभी समीकरणों के लिए किया जा सकता है; लेकिन डिग्री पांच या अधिक के समीकरणों को हमेशा इस तरह से हल नहीं किया जा सकता है, जैसा कि एबेल-रफिनी प्रमेय प्रदर्शित करता है।


x + y = a ; xy = b ......(2
एक अविभिन्न बीजगणितीय समीकरण ([[बहुपदों की मूल खोज]] देखें) और कई बहुभिन्नरूपी बहुपद समीकरणों के सामान्य समाधानों की वास्तविक संख्या या जटिल संख्या समाधानों के कुशलतापूर्वक सटीक अनुमानों की गणना करने के लिए बड़ी मात्रा में अनुसंधान समर्पित किया गया है ([[बहुपद समीकरणों की प्रणाली]] देखें) .


x² + y² = c ; xy = b ......(3)
=== रैखिक समीकरणों की प्रणाली ===
[[File:九章算術.gif|thumb|[[गणितीय कला पर नौ अध्याय]], दूसरी शताब्दी की एक अनामक चीनी पुस्तक है जो रेखीय समीकरणों के समाधान की एक विधि का प्रस्ताव करती है।]]रैखिक समीकरणों की एक प्रणाली (या रैखिक प्रणाली) एक या अधिक [[चर (गणित)]] से जुड़े रैखिक समीकरणों का एक संग्रह है।{{efn|The subject of this article is basic in mathematics, and is treated in a lot of textbooks. Among them, Lay 2005, Meyer 2001, and Strang 2005 contain the material of this article.}} उदाहरण के लिए,
:<math>\begin{alignat}{7}
3x &&\; + \;&& 2y            &&\; - \;&& z  &&\; = \;&& 1 & \\
2x &&\; - \;&& 2y            &&\; + \;&& 4z &&\; = \;&& -2 & \\
-x &&\; + \;&& \tfrac{1}{2} y &&\; - \;&& z  &&\; = \;&& 0 &
\end{alignat}</math>
तीन चरों में तीन समीकरणों की एक प्रणाली {{math|''x'', ''y'', ''z''}} है। एक रैखिक प्रणाली का समाधान चर के लिए संख्याओं का एक समनुदेशन है जिससे कि सभी समीकरण एक साथ संतुष्ट हों। उपरोक्त प्रणाली को हल करने वाला एक समीकरण निम्न द्वारा दिया गया है;
:<math>\begin{alignat}{2}
x &\,=\,& 1 \\
y &\,=\,& -2 \\
z &\,=\,& -2
\end{alignat}</math>
क्योंकि यह तीनों समीकरणों को मान्य बनाता है। प्रणाली शब्द इंगित करता है कि समीकरणों को अलग-अलग के स्थान पर सामूहिक रूप से माना जाना चाहिए।


x² + y² = c ; x + y = a ......(4)
गणित में, रेखीय प्रणालियों का सिद्धांत रेखीय बीजगणित का एक मूलभूत हिस्सा है, एक ऐसा विषय जो आधुनिक गणित के कई भागों में प्रयोग किया जाता है। समाधान खोजने के लिए संगणनात्मक [[कलन विधि]] [[संख्यात्मक रैखिक बीजगणित]] का एक महत्वपूर्ण हिस्सा हैं, और भौतिकी, [[अभियांत्रिकी]], [[रसायन विज्ञान]], [[कंप्यूटर विज्ञान|परिकलक विज्ञान]] और [[अर्थशास्त्र]] में एक प्रमुख भूमिका निभाते हैं। गैर-रैखिक समीकरणों की प्रणाली प्रायः एक रैखिक प्रणाली (रैखिकीकरण देखें) द्वारा अनुमानित हो सकती है, एक अपेक्षाकृत जटिल प्रणाली के गणितीय प्रतिरूप या [[कंप्यूटर सिमुलेशन|परिकलक]]  [[कंप्यूटर सिमुलेशन|अनुकरण]] बनाते समय एक सहायक तकनीक है।


(1) आर्यभट्ट प्रथम (499) के समाधान के लिए निम्नलिखित नियम बताता है:
== ज्यामिति ==


"गुणा के चार गुना (दो मात्राओं का) का वर्गमूल उनके अंतर के वर्ग के साथ जोड़ा जाता है, उनके अंतर से जोड़ा और घटाया जाता है और आधा दो गुणक देता है।"
=== विश्लेषणात्मक ज्यामिति ===
[[File:FunLin 04.svg|thumb|नीली और लाल रेखा सभी बिंदुओं (x,y) का सम्मुच्चय है जैसे क्रमशः x+y=5 और -x+2y=4। उनका [[चौराहा (यूक्लिडियन ज्यामिति)|प्रतिच्छेदन (यूक्लिडीय ज्यामिति)]] बिंदु, (2,3), दोनों समीकरणों को संतुष्ट करता है।]]
[[File:Coniques cone.png|thumb|एक शंक्वाकार खंड एक समतल और परिक्रमण के एक शंकु का प्रतिच्छेदन है।]]<nowiki> </nowiki>[[यूक्लिडियन ज्यामिति|यूक्लिडीय ज्यामिति]], स्थल में प्रत्येक बिंदु के लिए निर्देशांक का एक सम्मुच्चय जोड़ना संभव है, उदाहरण के लिए एक आयतीय संजाल द्वारा। यह विधि किसी को ज्यामितीय आकृतियों को समीकरणों द्वारा चिह्नित करने की अनुमति देती है। त्रि-आयामी अंतरिक्ष में एक विमान को फॉर्म के समीकरण के समाधान सम्मुच्चय के रूप में व्यक्त किया जा सकता है। <math> ax+by+cz+d=0</math>, जहाँ <math>a,b,c</math> और <math>d</math> वास्तविक संख्याएँ हैं और <math>x,y,z</math> अज्ञात हैं जो आयतीय संजाल द्वारा दी गई प्रणाली में एक बिंदु के निर्देशांक के अनुरूप हैं। मूल्य <math>a,b,c</math> समीकरण द्वारा परिभाषित समतल के लम्बवत् सदिश के निर्देशांक हैं। एक रेखा को दो समतलों के प्रतिच्छेदन के रूप में व्यक्त किया जाता है, जो कि मानों के साथ एकल रेखीय समीकरण के समाधान सम्मुच्चय <math>\mathbb{R}^2</math> के रूप में या मूल्यों के साथ दो रैखिक समीकरणों के समाधान सम्मुच्चय <math>\mathbb{R}^3</math> के रूप में होता है। 
एक [[शंकु]] खंड समीकरण <math>x^2+y^2=z^2</math> के साथ एक तल शंकु का प्रतिच्छेदन है। दूसरे शब्दों में, स्थल में, सभी शांकवों को तल के समीकरण और अभी दिए गए शंकु के समीकरण के हल समुच्चय के रूप में परिभाषित किया जाता है। यह औपचारिकता किसी को एक शंकु के केंद्रबिन्दु की स्थिति और गुणों को निर्धारित करने की अनुमति देती है।


यानी,
समीकरणों के उपयोग से ज्यामितीय प्रश्नों को हल करने के लिए गणित के एक बड़े क्षेत्र पर आवाहन करने की अनुमति मिलती है। कार्तीय समन्वय प्रणाली ज्यामितीय समस्या को एक विश्लेषण समस्या में बदल देती है, एक बार जब आंकड़े समीकरणों में परिवर्तित हो जाते हैं तो उनको विश्लेषणात्मक ज्यामिति नाम दिया जाता है। [[डेसकार्टेस]] द्वारा उल्लिखित यह दृष्टिकोण, प्राचीन ग्रीक गणितज्ञों द्वारा कल्पना की गई ज्यामिति के प्रकार को समृद्ध और संशोधित करता है।


<math>{\displaystyle x = {\frac{1}{2}}}({\sqrt{d^2+4b}}+d)</math> , <math>{\displaystyle y = {\frac{1}{2}}}({\sqrt{d^2+4b}}-d)</math>
वर्तमान में, विश्लेषणात्मक ज्यामिति गणित की एक सक्रिय शाखा को निर्दिष्ट करती है। हालांकि यह अभी भी आंकड़ों को चित्रित करने के लिए समीकरणों का उपयोग करता है, यह [[कार्यात्मक विश्लेषण]] और रैखिक बीजगणित जैसी अन्य परिष्कृत तकनीकों का भी उपयोग करता है।


ब्रह्मगुप्त (628) कहते हैं: "अवशेषों के अंतर के वर्ग के योग का वर्गमूल और अवशेषों के उत्पाद का दो वर्ग गुना, अवशेषों के अंतर से जोड़ा और घटाया जाता है, और आधा (देता है) वांछित अवशेष गंभीर रूप से।"
=== कार्तीय समीकरण ===
कार्तीय [[समन्वय प्रणाली]] एक समन्वय प्रणाली है जो प्रत्येक [[बिंदु (ज्यामिति)]] को विशिष्ट रूप से एक तल (ज्यामिति) में [[संख्या]] निर्देशांक की एक जोड़ी द्वारा निर्दिष्ट करती है, जो कि धनात्मक और ऋणात्मक संख्याएँ हैं, जो लंबाई की एक ही इकाई का उपयोग करके चिह्नित किए गए हैं।


नारायण (1357) लिखते हैं: "दो मात्राओं के अंतर के वर्ग का वर्गमूल उनके गुणनफल का चार गुना होता है।"
तीन कार्तीय निर्देशांकों के उपयोग से त्रि-आयामी [[अंतरिक्ष (गणित)|स्थल (गणित)]] में किसी भी बिंदु की स्थिति निर्दिष्ट करने के लिए एक ही सिद्धांत का उपयोग किया जा सकता है, जो तीन परस्पर लंबवत  तल  के लिए हस्ताक्षरित दूरी हैं (या, समतुल्य रूप से, इसके लंबवत प्रक्षेपण द्वारा तीन परस्पर लंबवत रेखाओं पर हस्ताक्षरित है)।


"मात्राओं के अंतर का वर्ग उनके गुणनफल के दुगुने के साथ उनके वर्गों के योग के बराबर होता है। इस परिणाम का वर्गमूल जोड़ गुणन का दोगुना योग होता है।"
[[File:Cartesian-coordinate-system-with-circle.svg|thumb|right|लाल रंग में चिह्नित मूल पर केंद्रित त्रिज्या 2 के एक चक्र के साथ कार्टेशियन समन्वय प्रणाली। एक वृत्त का समीकरण {{nowrap|1=(''x'' − ''a'')<sup>2</sup> + (''y'' − ''b'')<sup>2</sup> = ''r''<sup>2</sup>}} है, जहाँ a और b केंद्र के निर्देशांक हैं {{nowrap|(''a'', ''b'')}} और R त्रिज्या है।]]17 वीं शताब्दी में रेने डेसकार्टेस (लैटिनीकरण (साहित्य) नाम: कार्टेसियस) द्वारा कार्तीय निर्देशांक के आविष्कार ने यूक्लिडियन ज्यामिति और बीजगणित के बीच पहला व्यवस्थित कड़ी प्रदान करके गणित में क्रांति ला दी। कार्तीय समन्वय प्रणाली का उपयोग करते हुए, ज्यामितीय आकृतियों (जैसे घटता) को 'कार्तीय समीकरण' द्वारा वर्णित किया जा सकता है: बीजगणितीय समीकरण जिसमें आकृति पर स्थित बिंदुओं के निर्देशांक सम्मिलित होते हैं। उदाहरण के लिए, एक समतल में त्रिज्या 2 का एक वृत्त, जो एक विशेष बिंदु पर केन्द्रित होता है जिसे मूल कहा जाता है, को उन सभी बिंदुओं के समुच्चय के रूप में वर्णित किया जा सकता है जिनके निर्देशांक x और y समीकरण {{nowrap|1=''x''<sup>2</sup> + ''y''<sup>2</sup> = 4}} को संतुष्ट करते हैं।


(2) के समाधान के लिए महावीर (850) द्वारा निम्नलिखित नियम दिया गया है: "अर्ध-परिधि के वर्ग से क्षेत्रफल (एक आयत का) का चार गुना घटाएँ, फिर उस (शेष) के वर्गमूल के बीच ''संक्रमण'' द्वारा ) और अर्ध-परिधि, आधार और अपराइट प्राप्त होते हैं।"
=== प्राचलिक समीकरण ===
{{main|प्राचलिक समीकरण}}
एक वक्र के लिए एक प्राचलिक समीकरण वक्र के बिंदुओं के निर्देशांक को एक चर (गणित) के कार्यों के रूप में व्यक्त करता है, जिसे एक मापदण्ड कहा जाता है।<ref>Thomas, George B., and Finney, Ross L., ''Calculus and Analytic Geometry'', Addison Wesley Publishing Co., fifth edition, 1979, p. 91.</ref><ref>Weisstein, Eric W. "Parametric Equations." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/ParametricEquations.html</ref> उदाहरण के लिए,
:<math>\begin{align}
x&=\cos t\\
y&=\sin t
\end{align}</math>
[[यूनिट सर्कल|एकक वृत्त]] के लिए प्राचलिक समीकरण हैं, जहां t मापदण्ड है। साथ में, इन समीकरणों को वक्र का 'प्राचलिक प्रतिनिधित्व' कहा जाता है।


<math>{\displaystyle x = {\frac{1}{2}}}(a + {\sqrt{a^2-4b}})</math>
प्राचलिक समीकरण की धारणा को [[सतह (टोपोलॉजी)|सतह (सांस्थिति)]], बहुआयामी और उच्च आयाम के बीजगणितीय [[विविध]]ता के लिए सामान्यीकृत किया गया है, जिसमें  बहुरूपता या विविधता के आयाम के बराबर मापदंडों की संख्या और समीकरणों की संख्या के बराबर है। उस स्थान का आयाम जिसमें बहुरूपता या विविधता पर विचार किया जाता है (वक्र के लिए आयाम एक है और सतहों के आयाम दो और दो मापदण्ड आदि के लिए एक मापदण्ड का उपयोग किया जाता है)।


<math>{\displaystyle y = {\frac{1}{2}}}(a - {\sqrt{a^2-4b}})</math>
== संख्या सिद्धांत ==


नारायण कहते हैं: "योग के वर्ग का वर्गमूल गुणनफल के चार गुना का अंतर है।"
=== डायोफैंटाइन समीकरण ===
{{main|डायोफैंटाइन समीकरण}}


(3) के लिए महावीर नियम देता है: "विकर्ण के वर्ग से (एक आयत के) क्षेत्र में दो बार जोड़ें और घटाएं और वर्गमूल निकालें। इनमें से बड़े और छोटे (मूलों) के बीच संक्रामण द्वारा, पक्ष और सीधे पाए जाते हैं।
एक डायोफैंटाइन समीकरण दो या दो से अधिक अज्ञात में एक बहुपद समीकरण है जिसके लिए केवल पूर्णांक समाधान मांगे जाते हैं (एक पूर्णांक समाधान ऐसा समाधान है कि सभी अज्ञात पूर्णांक मान लेते हैं)। एक रेखीय डायोफैंटाइन समीकरण एक बहुपद शून्य या एक की डिग्री के दो योगों के बीच का समीकरण है। रेखीय डायोफैंटाइन समीकरण का एक उदाहरण {{math|''ax'' + ''by'' {{=}} ''c''}} है, जहाँ a, b और c स्थिरांक हैं। एक 'घातीय डायोफैंटाइन समीकरण' वह है जिसके लिए समीकरण की शर्तों के प्रतिपादक अज्ञात हो सकते हैं।


<math>{\displaystyle x = {\frac{1}{2}}}({\sqrt{c+2b}}  +  {\sqrt{c-2b}})</math>
'डायोफैंटाइन समस्याओं' में अज्ञात चरों की तुलना में कम समीकरण होते हैं और इसमें सभी समीकरणों के लिए सही ढंग से काम करने वाले पूर्णांकों को खोजना सम्मिलित होता है। अधिक तकनीकी भाषा में, वे एक [[बीजगणितीय वक्र]], [[बीजगणितीय सतह]], या अधिक सामान्य वस्तु को परिभाषित करते हैं, और उस पर [[जाली बिंदु|जालक बिंदु]]ओं के बारे में पूछते हैं।


<math>{\displaystyle y = {\frac{1}{2}}}({\sqrt{c+2b}}  -  {\sqrt{c-2b}})</math>
डायोफैंटाइन शब्द तीसरी शताब्दी के हेलेनिस्टिक गणितज्ञ, अलेक्जेंड्रिया के डायोफैंटस को संदर्भित करता है, जिन्होंने इस तरह के समीकरणों का अध्ययन किया और बीजगणित में प्रतीकवाद को प्रस्तुत करने वाले पहले गणितज्ञों में से एक थे।। डायोफैंटाइन समस्याओं का गणितीय अध्ययन जिसे डायोफैंटस ने शुरू किया था, उसे अब 'डायोफैंटाइन विश्लेषण' कहा जाता है।


समीकरणों के लिए (4) आर्यभट्ट I लिखते हैं: "योग के वर्ग से (दो राशियों का) उनके वर्गों का योग घटाएं। शेष का आधा उनका उत्पाद है।"
===बीजगणितीय और पारलौकिक संख्याएं===
{{main|बीजगणितीय संख्या|पारलौकिक संख्या}}


शेष संक्रियाएं समीकरणों (2) के समान होंगी; ताकि
[[बीजगणितीय संख्या]] एक संख्या है जो परिमेय संख्या गुणांकों के साथ चर में एक गैर-शून्य बहुपद समीकरण का एक समाधान है (या समतुल्य - समाशोधन हर द्वारा - पूर्णांक गुणांक के साथ)। π जैसी संख्याएँ जो बीजगणितीय नहीं हैं, उन्हें पारलौकिक कहा जाता है। लगभग सभी वास्तविक और सम्मिश्र संख्याएँ पारलौकिक हैं।


<math>{\displaystyle x = {\frac{1}{2}}}(a + {\sqrt{2c-a^2}})</math>
=== बीजगणितीय ज्यामिति ===
{{main|बीजगणितीय ज्यामिति}}
बीजगणितीय [[ज्यामिति]] गणित की एक शाखा है, जो शास्त्रीय रूप से बहुपद समीकरणों के समाधान का अध्ययन करती है। आधुनिक बीजगणितीय ज्यामिति भाषा और ज्यामिति की समस्याओं के साथ अमूर्त बीजगणित की अधिक अमूर्त तकनीकों, विशेष रूप से [[क्रमविनिमेय बीजगणित]] पर आधारित है।


<math>{\displaystyle y = {\frac{1}{2}}}(a - {\sqrt{2c-a^2}})</math>
बीजगणितीय ज्यामिति में अध्ययन की मूलभूत वस्तुएँ बीजगणितीय विविधता हैं, जो बहुपद समीकरणों के प्रणाली के [[समाधान सेट|समाधान सम्मुच्चय]] की ज्यामितीय अभिव्यक्तियाँ हैं। बीजगणितीय किस्मों के सबसे अधिक अध्ययन किए गए वर्गों के उदाहरण हैं: समतल बीजगणितीय वक्र, जिसमें रेखाएँ, वृत्त, परवलय, दीर्घवृत्त, अतिपरवलय, घनीय वक्र जैसे अण्डाकार वक्र और क्वार्टिक वक्र जैसे लेम्निस्केट्स और कैसिनी अंडाकार सम्मिलित हैं। यदि इसके निर्देशांक दिए गए बहुपद समीकरण को संतुष्ट करते हैं तो समतल का एक बिंदु एक बीजगणितीय वक्र से संबंधित होता है। मूल प्रश्नों में वक्र के एकवचन बिंदु, विभक्ति बिंदु और [[अनंत पर बिंदु]] जैसे विशेष रुचि के बिंदुओं का अध्ययन सम्मिलित है। अधिक उन्नत प्रश्नों में वक्र की [[टोपोलॉजी|सांस्थिति]] और विभिन्न समीकरणों द्वारा दिए गए वक्रों के बीच संबंध सम्मिलित होते हैं।


ब्रह्मगुप्त कहते हैं: "योग के वर्ग को वर्गों के योग के दोगुने से घटाएं; शेष का वर्गमूल योग में जोड़ा और घटाया और आधा किया जाता है, वांछित अवशेष देता है।"
== विभेदक समीकरण ==
{{main|विभेदक समीकरण}}
[[File:Attracteur étrange de Lorenz.png|thumb|एक [[अजीब आकर्षण|असामान्य आकर्षण]], जो एक निश्चित [[अंतर समीकरण]] को हल करते समय उत्पन्न होता है]]अवकल समीकरण एक गणित का समीकरण है जो कुछ फलनों (गणित) को उसके अवकलजों से संबंधित करता है। अनुप्रयोगों में, कार्य सामान्यतः भौतिक मात्रा का प्रतिनिधित्व करते हैं, [[यौगिक]] परिवर्तन की अपनी दरों का प्रतिनिधित्व करते हैं, और समीकरण दोनों के बीच संबंध को परिभाषित करता है। क्योंकि इस तरह के संबंध अत्यंत सामान्य हैं, भौतिक विज्ञान,  अभियान्त्रिकी, अर्थशास्त्र और जीव विज्ञान सहित कई विषयों में अवकल समीकरण प्रमुख भूमिका निभाते हैं।


नारायण ने एक साथ द्विघात समीकरणों के दो अन्य रूप दिए हैं, अर्थात्,
[[शुद्ध गणित]] में, अंतर समीकरणों का कई अलग-अलग दृष्टिकोणों से अध्ययन किया जाता है, जो अधिकतर उनके समीकरण को संतुष्ट करने वाले कार्यों के सम्मुच्चय से संबंधित होते हैं।  स्पष्ट सूत्रों द्वारा केवल सबसे सरल अवकल समीकरणों को हल किया जा सकता है; हालाँकि, किसी दिए गए अवकल समीकरण के समाधान के कुछ गुण उनके सटीक रूप को खोजे बिना निर्धारित किए जा सकते हैं।


<math>x^2+y^2=c </math>      x - y = d.....(5)
यदि समाधान के लिए स्व-निहित सूत्र उपलब्ध नहीं है, तो परिकलक का उपयोग करके समाधान को संख्यात्मक रूप से अनुमानित किया जा सकता है। गतिशील प्रणालियों का सिद्धांत अंतर समीकरणों द्वारा वर्णित प्रणालियों के गुणात्मक विश्लेषण पर जोर देता है, जबकि सटीकता की एक निश्चित डिग्री के साथ समाधान निर्धारित करने के लिए कई [[संख्यात्मक तरीके]] विकसित किए गए हैं।


<math>x^2-y^2=m</math>    xy = b ......(6)
=== साधारण अंतर समीकरण ===
{{main|साधारण विभेदक समीकरण}}
[[साधारण अंतर समीकरण]] या ODE एक समीकरण है जिसमें [[स्वतंत्र चर]] और उसके  व्युत्पादित का एक कार्य होता है। ''साधारण'' शब्द का प्रयोग आंशिक अंतर समीकरण के विपरीत किया जाता है, जो एक स्वतंत्र चर ''से अधिक'' के संबंध में हो सकता है।


(5) के समाधान के लिए वह नियम देता है: "वर्गों के योग के दोगुने का वर्गमूल अंतर के वर्ग द्वारा घटाए गए के बराबर है
रेखीय अवकल समीकरण, जिनके ऐसे हल हैं जिन्हें गुणांकों द्वारा जोड़ा और गुणा किया जा सकता है, अच्छी तरह से परिभाषित और समझा जाता है, और सटीक बंद-रूप समाधान प्राप्त होते हैं। इसके विपरीत, ODE जिनमें योगात्मक समाधानों की कमी होती है, अरैखिक होते हैं, और उन्हें हल करना कहीं अधिक जटिल होता है, क्योंकि बंद रूप में [[प्राथमिक कार्य|प्राथमिक]] कार्यों द्वारा शायद ही कभी उनका प्रतिनिधित्व किया जा सकता है: इसके बजाय, ODE के सटीक और विश्लेषणात्मक समाधान श्रृंखला या अभिन्न रूप में होते हैं। हाथ से या परिकलक द्वारा लागू आलेखीय और [[संख्यात्मक साधारण अंतर समीकरण]] पद्धति, ODE के समाधान का अनुमान लगा सकते हैं और शायद उपयोगी जानकारी प्राप्त कर सकते हैं, जो प्रायः सटीक, विश्लेषणात्मक समाधान के अभाव में पर्याप्त होती है।


योग।"
=== आंशिक अंतर समीकरण ===
{{main|आंशिक अंतर समीकरण}}


<math>{\displaystyle x +y = {\sqrt{2c-d^2}}}</math>
एक आंशिक अंतर समीकरण (PDE) एक अंतर समीकरण है जिसमें अज्ञात बहुभिन्नरूपी कलन और उनके आंशिक  व्युत्पादित सम्मिलित हैं। (यह सामान्य अंतर समीकरणों के विपरीत है, जो एक चर और उनके  व्युत्पादित के कार्यों से निपटते हैं।) PDE का उपयोग कई चर के कार्यों से जुड़ी समस्याओं को तैयार करने के लिए किया जाता है, और या तो हाथ से हल किया जाता है, या एक प्रासंगिक [[कंप्यूटर मॉडल|परिकलक प्रतिरूप]] बनाने के लिए उपयोग किया जाता है। .


इसलिए
PDE का उपयोग विभिन्न प्रकार की घटनाओं जैसे ध्वनि, [[गर्मी]], [[इलेक्ट्रोस्टाटिक्स|स्थिर विद्युतिकी]], [[बिजली का गतिविज्ञान]], द्रव प्रवाह, [[लोच (भौतिकी)]], या [[क्वांटम यांत्रिकी|परिमाण यांत्रिकी]] का वर्णन करने के लिए किया जा सकता है। PDE के संदर्भ में समान रूप से अलग-अलग भौतिक घटनाओं को औपचारिक रूप दिया जा सकता है। जिस तरह साधारण अंतर समीकरण प्रायः एक-आयामी गतिशील प्रणालियों का प्रतिरूप करते हैं, आंशिक अंतर समीकरण प्रायः बहुआयामी प्रणालियों का प्रतिरूप करते हैं। PDE अपने सामान्यीकरण को प्रसंभाव्य आंशिक अंतर समीकरणों में पाते हैं।


<math>{\displaystyle x = {\frac{1}{2}}}({\sqrt{2c-d^2}}+d)</math>
== समीकरणों के प्रकार ==
<!--Linked from [[Simultaneous equations]]-->
समीकरणों को संक्रिया के प्रकार (गणित) और सम्मिलित मात्राओं के अनुसार वर्गीकृत किया जा सकता है। महत्वपूर्ण प्रकारों में सम्मिलित हैं:
* एक [[बीजगणितीय समीकरण]] या बहुपद समीकरण एक समीकरण है जिसमें दोनों पक्ष बहुपद होते हैं  बहुपद समीकरणों की प्रणाली भी देखें)। इन्हें बहुपद की डिग्री द्वारा आगे वर्गीकृत किया गया है:
** डिग्री एक के लिए [[पारलौकिक समारोह]]
** डिग्री दो के लिए द्विघात समीकरण
** डिग्री तीन के लिए [[घन समीकरण]]
** डिग्री चार के लिए क्वार्टिक समीकरण
** डिग्री पांच के लिए क्विंटिक समीकरण
** छह डिग्री के लिए सिस्टिक समीकरण
** डिग्री सात के लिए [[सेप्टिक समीकरण]]
** डिग्री आठ के लिए [[ऑक्टिक समीकरण]]
* एक [[डायोफैंटाइन समीकरण]] एक समीकरण है जहां अज्ञात को पूर्णांक होना आवश्यक है
* एक अनुभवातीत समीकरण एक ऐसा समीकरण है जिसमें इसके अज्ञात का एक [[पारलौकिक समीकरण]] सम्मिलित है
* प्राचलिक समीकरण एक ऐसा समीकरण है जिसमें चरों के समाधान को कुछ अन्य चरों के कार्यों के रूप में व्यक्त किया जाता है, जिन्हें समीकरणों में प्रदर्शित होने वाले मापदण्ड कहा जाता है
* एक [[कार्यात्मक समीकरण]] एक ऐसा
*समीकरण है जिसमें अज्ञात सामान्य मात्रा के बजाय कार्य (गणित) हैं
* व्युत्पादित, संपूर्ण और परिमित अंतर वाले समीकरण:
** एक अंतर समीकरण एक कार्यात्मक समीकरण है जिसमें अज्ञात कार्यों के व्युत्पादित सम्मिलित होते हैं, जहां प्रकार्य और उसके  व्युत्पादित का मूल्यांकन एक ही बिंदु पर किया जाता है, जैसे कि <math>f'(x) = x^2</math>. अवकल समीकरणों को एकल चर वाले फलनों के लिए सामान्य अवकल समीकरणों और अनेक चरों वाले फलनों के लिए आंशिक अवकल समीकरणों में उप-विभाजित किया जाता है।
** एक [[अभिन्न समीकरण]] एक कार्यात्मक समीकरण है जिसमें अज्ञात कार्यों के प्रतिपक्षी सम्मिलित हैं। चर के कार्यों के लिए, ऐसा समीकरण एक अंतर समीकरण से भिन्न होता है, मुख्य रूप से इसके व्युत्पन्न द्वारा प्रकार्य को प्रतिस्थापित करने वाले चर के परिवर्तन के माध्यम से, हालांकि यह मामला नहीं है जब अभिन्न एक खुली सतह पर लिया जाता है
** एक पूर्णांक-अंतर समीकरण एक कार्यात्मक समीकरण है जिसमें अज्ञात कार्यों के  व्युत्पादित और [[antiderivative|एंटीडेरिवेटिव]] दोनों सम्मिलित हैं। एक चर के कार्यों के लिए, ऐसा समीकरण चर के समान परिवर्तन के माध्यम से अभिन्न और अंतर समीकरणों से भिन्न होता है।
** [[देरी अंतर समीकरण]] का एक [[कार्यात्मक अंतर समीकरण]] एक प्रकार्य समीकरण है जिसमें अज्ञात कार्यों के  व्युत्पादित सम्मिलित हैं, जिनका मूल्यांकन कई बिंदुओं पर किया जाता है, जैसे <math>f'(x) = f(x-2)</math>
** एक [[अंतर समीकरण]] एक समीकरण है जहां अज्ञात एक फलन f है जो समीकरण में f(x), f(x−1), ..., f(x−k) के  माध्यम से होता है, कुछ पूर्ण पूर्णांक k के लिए कहा जाता है समीकरण का क्रम। यदि x को एक पूर्णांक के रूप में प्रतिबंधित किया जाता है, तो एक अंतर समीकरण [[पुनरावृत्ति संबंध]] के समान होता है
** एक [[स्टोचैस्टिक अंतर समीकरण]] एक अंतरात्मक समीकरण है जिसमें एक या अधिक शब्द एक प्रसंभाव्य प्रक्रिया है


<math>{\displaystyle y = {\frac{1}{2}}}({\sqrt{2c-d^2}}-d)</math>
== यह भी देखें ==
{{Div col|colwidth=25em}}
* सूत्र
* [[बीजगणित का इतिहास]]
* [[अनिश्चित समीकरण]]
* [[समीकरणों की सूची]]
* [[लोगों के नाम पर वैज्ञानिक समीकरणों की सूची]]
* [[अवधि (तर्क)]]
* [[समीकरणों का सिद्धांत]]
* रद्द करना
{{Div col end}}




(6)  के लिए नारायण लिखते हैं: "-
==टिप्पणियाँ==
{{notelist}}


"मान लीजिए कि गुणनफल का वर्ग गुणनफल (दो मात्राओं का) और वर्गों का अंतर उनके अंतर के रूप में है। उनसे संक्रम द्वारा (वर्ग) मात्राएँ प्राप्त की जाएंगी। उनके वर्गमूल अलग-अलग मात्राएँ (आवश्यक) देंगे। ।"


हमारे पास है
==संदर्भ==
{{reflist}}


x² - y² =m


x² y² = b<sup>2</sup>


ये रूप (1) के हैं। इसलिए
*
== बाहरी कड़ियाँ ==
* [https://web.archive.org/web/20090816161008/http://math.exeter.edu/rparris/winplot.html Winplot]: General Purpose plotter that can draw and animate 2D and 3D mathematical equations.
* [http://www.cs.cornell.edu/w8/~andru/relplot Equation plotter]: A web page for producing and downloading pdf or postscript plots of the solution sets to equations and inequations in two variables (''x'' and ''y'').


<math>{\displaystyle x^2 = {\frac{1}{2}}}({\sqrt{m^2+4b^2}}+m)</math>
{{Authority control}}
[[श्रेणी: प्रारंभिक बीजगणित]]
[[श्रेणी:समीकरण| ]]


<math>{\displaystyle y^2 = {\frac{1}{2}}}({\sqrt{m^2+4b^2}}-m)</math>


अब हम x और y के मान प्राप्त करते हैं।
[[Category: Machine Translated Page]]
[[Category:गणित]]
[[Category:Created On 19/12/2022]]
<references />
[[Category:Vigyan Ready]]

Latest revision as of 16:58, 23 December 2022

For other uses, see समीकरण (disambiguation).
आधुनिक अंकन में 14x + 15 = 71 के समतुल्य एक बराबर चिह्न का पहला उपयोग। वेल्स के रॉबर्ट रिकॉर्डे द्वारा द वेटस्टोन ऑफ़ विट से (1557)।[1]

गणित में, एक समीकरण एक सूत्र है जो दो व्यंजकों (गणित) की समानता (गणित) को बराबर के चिह्न = से जोड़कर व्यक्त करता है। [2][3] अन्य भाषाओं में शब्द समीकरण और इसके सजातीय अर्थों में सूक्ष्म रूप से भिन्न अर्थ हो सकते हैं; उदाहरण के लिए, फ्रांसीसी भाषा में एक समीकरण को एक या एक से अधिक चर (गणित) के रूप में परिभाषित किया जाता है, जबकि अंग्रेजी भाषा में, बराबर चिह्न से संबंधित दो अभिव्यक्तियों से युक्त कोई भी अच्छी तरह से तैयार सूत्र एक समीकरण है।[4]

चर वाले समीकरण को हल करने में यह निर्धारित करना सम्मिलित है कि चर के कौन से मान समानता को सत्य बनाते हैं। वे चर जिनके लिए समीकरण को हल करना होता है, 'अज्ञात' भी कहलाते हैं, और अज्ञात के वे मान जो समानता को संतुष्ट करते हैं, समीकरण के हल (समीकरण) कहलाते हैं। समीकरण दो प्रकार के होते हैं: सर्वसमिका (गणित) और सशर्त समीकरण। चर के सभी मूल्यों के लिए एक सर्वसमिका सत्य है। सशर्त समीकरण केवल चरों के विशेष मानों के लिए सत्य होता है।[5][6]

एक समीकरण को दो व्यंजकों (गणित) के रूप में लिखा जाता है, जो बराबर चिह्न (=) से जुड़ा होता है।[2] बराबर के चिह्न वाले समीकरण के दोनों पक्षों के व्यंजक समीकरण के बाएँ पक्ष और दाएँ पक्ष कहलाते हैं। बहुत बार किसी समीकरण के दाहिने पक्ष को शून्य मान लिया जाता है। यह मानने से व्यापकता कम नहीं होती है, क्योंकि इसे दोनों पक्षों से दाहिनी ओर घटाकर महसूस किया जा सकता है।

सबसे सामान्य प्रकार का समीकरण एक [[बहुपद समीकरण]] है (सामान्यतः इसे बीजगणितीय समीकरण भी कहा जाता है) जिसमें दो पक्ष बहुपद होते हैं। एक बहुपद समीकरण के पक्षों में एक या एक से अधिक योग संकेत और शब्दावली होती है। उदाहरण के लिए, समीकरण

बाईं ओर है, जिसमें चार पद हैं, और दाहिनी ओर, केवल एक शब्द से मिलकर है। चर (गणित) के नाम बताते हैं कि x और y अज्ञात हैं, और वह A, B, और C मापदण्ड हैं, लेकिन यह सामान्य रूप से संदर्भ द्वारा तय किया जाता है (कुछ संदर्भों में, y एक मापदण्ड हो सकता है, या A, B, और C साधारण चर हो सकते हैं)।

एक समीकरण उस पैमाने के अनुरूप होता है जिसमें वजन रखा जाता है। जब किसी चीज़ के बराबर वज़न (जैसे, अनाज) को दो पलड़ों में रखा जाता है, तो दो वज़न तराजू को संतुलन में रखते हैं और उन्हें बराबर कहा जाता है। यदि पलड़े के एक पलड़े में से अन्न की गिनती निकाली जाए, तो पलड़े को सन्तुलित रखने के लिथे दूसरे पलड़े में से भी उतना ही अन्न निकाला जाए। अधिक सामान्यतः, एक समीकरण संतुलन में रहता है यदि इसके दोनों पक्षों पर एक ही संचालन किया जाता है।

कार्तीय ज्यामिति में, ज्यामितीय आकृतियों का वर्णन करने के लिए समीकरणों का उपयोग किया जाता है। जैसा कि जिन समीकरणों पर विचार किया जाता है, जैसे निहित समीकरण या प्राचलिक समीकरण, के असीम रूप से कई समाधान होते हैं, उद्देश्य अब अलग है: समाधानों को स्पष्ट रूप से देने या उन्हें गिनने के बजाय, जो असंभव है, आंकड़ों के गुणों का अध्ययन करने के लिए समीकरणों का उपयोग किया जाता है। यह बीजगणितीय ज्यामिति का प्रारंभिक विचार है, जो गणित का एक महत्वपूर्ण क्षेत्र है।

बीजगणित समीकरणों के दो मुख्य परिवारों का अध्ययन करता है: बहुपद समीकरण और उनमें से, रैखिक समीकरणों का विशेष मामला। चूंकि जिन समीकरणों पर विचार किया जाता है, जैसे अंतर्निहित समीकरण या प्राचलिक समीकरण, उनके असीम रूप से कई समाधान होते हैं, उद्देश्य अब अलग है: समाधानों को स्पष्ट रूप से देने या उन्हें गिनने के बजाय, जो असंभव है, आंकड़ों के गुणों का अध्ययन करने के लिए समीकरणों का उपयोग किया जाता है। बीजगणित डायोफैंटाइन समीकरणों का भी अध्ययन करता है जहां गुणांक और समाधान पूर्णांक होते हैं। उपयोग की जाने वाली तकनीकें भिन्न हैं और संख्या सिद्धांत से आती हैं। ये समीकरण सामान्य तौर पर कठिन होते हैं; कोई प्रायः समाधान के अस्तित्व या अनुपस्थिति को खोजने के लिए खोज करता है, और यदि वे मौजूद हैं, तो समाधानों की संख्या गिनने के लिए मौजूद हैं।

विभेदक समीकरण ऐसे समीकरण होते हैं जिनमें एक या अधिक कार्य और उनके व्युत्पादित सम्मिलित होते हैं। वे उस फलन के लिए एक व्यंजक खोज कर हल किए जाते हैं जिसमें अवकलज सम्मिलित नहीं है। विभेदक समीकरणों का उपयोग प्रतिरूप प्रक्रियाओं के लिए किया जाता है जिसमें चर के परिवर्तन की दर सम्मिलित होती है, और भौतिकी, रसायन विज्ञान, जीव विज्ञान और अर्थशास्त्र जैसे क्षेत्रों में उपयोग किया जाता है।

= प्रतीक, जो हर समीकरण में प्रकट होता है, का आविष्कार 1557 में रॉबर्ट रिकॉर्डे द्वारा किया गया था, जिन्होंने माना था कि समान लंबाई वाली समानांतर सीधी रेखाओं से अधिक समान कुछ भी नहीं हो सकता है।[1]


परिचय

अनुरूप चित्रण

एक साधारण समीकरण का चित्रण; x, y, z वास्तविक संख्याएँ हैं, जो वज़न के समान हैं।

एक समीकरण एक वजनी पैमाने, तराजू या झूले के समान होता है।

समीकरण का प्रत्येक पक्ष संतुलन के एक पक्ष से मेल खाता है। प्रत्येक पक्ष पर अलग-अलग मात्राएँ रखी जा सकती हैं: यदि दोनों पक्षों पर भार समान हैं, तो तराजू संतुलित करता है, और सादृश्यता में, संतुलन का प्रतिनिधित्व करने वाली समानता भी संतुलित होती है (यदि नहीं, तो संतुलन की कमी एक असमानता से मेल खाती है ( गणित) एक असमिका द्वारा दर्शाया गया है)।

उदाहरण में, x, y और z सभी अलग-अलग मात्राएँ हैं (इस मामले में वास्तविक संख्याएँ) जिन्हें गोलाकार भार के रूप में दर्शाया गया है, और x, y और z में से प्रत्येक का अलग-अलग वज़न है। योग वजन जोड़ने के अनुरूप है, जबकि घटाव पहले से मौजूद वजन को हटाने से मेल खाता है। जब समानता धारण करती है, तो प्रत्येक पक्ष का कुल भार समान होता है।

मापदण्ड एवं अपरिचित

See also: अभिव्यक्ति (गणित)

समीकरणों में प्रायः अज्ञात के अतिरिक्त अन्य पद होते हैं। ये अन्य शब्द, जिन्हें ज्ञात माना जाता है, सामान्यतः स्थिरांक, गुणांक या मापदण्ड कहलाते हैं।

x और y को अज्ञात के रूप में सम्मिलित करने वाले समीकरण का एक उदाहरण और मापदण्ड R है

जब R को 2 (R = 2) के मान के लिए चुना जाता है, तो इस समीकरण को कार्तीय निर्देशांक में मूल के चारों ओर 2 के त्रिज्या के चक्र के समीकरण के रूप में सर्वसमिकाा जाएगा। इसलिए, R अनिर्दिष्ट के साथ समीकरण चक्र के लिए सामान्य समीकरण है।

सामान्यतः, अज्ञात को वर्णमाला के अंत में अक्षरों द्वारा दर्शाया जाता है, x, y, z, w, ..., जबकि गुणांक (मापदण्ड) शुरुआत में अक्षरों द्वारा दर्शाए जाते हैं, a, b, c, d, .. ... उदाहरण के लिए, सामान्य द्विघात समीकरण को सामान्यतः ax2+ bx+ c = 0 लिखा जाता है.

समाधान खोजने की प्रक्रिया, या, मापदंडों के मामले में, अज्ञात को मापदंडों के संदर्भ में व्यक्त करना, समीकरण हल करना कहलाता है। मापदंडों के संदर्भ में समाधानों की ऐसी अभिव्यक्तियाँ भी समाधान कहलाती हैं।

समीकरणों की एक प्रणाली एक साथ समीकरणों का एक सम्मुच्चय है, सामान्यतः कई अविदित में जिसके लिए सामान्य समाधान मांगे जाते हैं। इस प्रकार, प्रणाली का समाधान प्रत्येक अज्ञात के लिए मूल्यों का एक सम्मुच्चय है, जो एक साथ प्रणाली में प्रत्येक समीकरण का समाधान बनाते हैं। उदाहरण के लिए, प्रणाली

अद्वितीय समाधान x= −1, y=1 है।

सर्वसमिका

Main articles: सर्वसमिका (गणित) and त्रिकोणमितीय सर्वसमिकाओं की सूची

एक सर्वसमिका एक समीकरण है जो इसमें निहित चर(नों) के सभी संभावित मानों के लिए सत्य है। बीजगणित और कलन में अनेक सर्वसमिकाएँ ज्ञात हैं। एक समीकरण को हल करने की प्रक्रिया में, एक समीकरण को सरल बनाने के लिए प्रायः एक सर्वसमिका का उपयोग किया जाता है, जिससे इसे अधिक आसानी से हल किया जा सकता है।

बीजगणित में, एक सर्वसमिका का उदाहरण दो वर्गों का अंतर है:

जो सभी x और y के लिए सत्य है।

त्रिकोणमिति एक ऐसा क्षेत्र है जहां कई सर्वसमिका मौजूद हैं; ये त्रिकोणमितीय समीकरणों में हेरफेर करने या हल करने में उपयोगी होते हैं। कई में से दो जिनमें द्विज्या और कोटिज्या प्रकार्य सम्मिलित हैं:

और

जो θ के सभी मानों के लिए सत्य हैं।

उदाहरण के लिए, समीकरण को संतुष्ट करने वाले θ के मान को हल करने के लिए:

जहां θ 0 और 45 डिग्री के बीच सीमित है, कोई उत्पाद देने के लिए उपरोक्त सर्वसमिका का उपयोग कर सकता है:

θ के लिए निम्नलिखित समाधान प्राप्त करना:

चूँकि ज्या फलन एक आवर्ती फलन है, यदि θ पर कोई प्रतिबंध नहीं है तो इसके अपरिमित रूप से अनेक समाधान हैं। इस उदाहरण में, θ को 0 और 45 डिग्री के बीच सीमित करने से समाधान केवल एक संख्या तक सीमित हो जाएगा।

गुण

दो समीकरण या समीकरणों की दो प्रणालियाँ समतुल्य होती हैं, यदि उनके हलों का एक ही समुच्चय हो। निम्नलिखित संक्रियाएँ एक समीकरण या समीकरणों की एक प्रणाली को एक समतुल्य में बदल देती हैं - बशर्ते कि संक्रियाएँ उन व्यंजकों के लिए सार्थक हों जिन पर वे लागू होते हैं:

  • किसी समीकरण के दोनों पक्षों में समान मात्रा को जोड़ना या घटाना। इससे पता चलता है कि प्रत्येक समीकरण उस समीकरण के तुल्य होता है जिसमें दाहिनी ओर शून्य होता है।
  • एक समीकरण के दोनों पक्षों को एक गैर-शून्य मात्रा से गुणा या विभाजित करना।
  • समीकरण के एक पक्ष को बदलने के लिए एक सर्वसमिका (गणित) लागू करना। उदाहरण के लिए, बहुपद विस्तार एक उत्पाद या बहुपदों का गुणन योग है।
  • एक प्रणाली के लिए एक समीकरण के दोनों पक्षों में दूसरे समीकरण के संबंधित पक्ष को जोड़कर, समान मात्रा से गुणा किया जाता है।

यदि किसी समीकरण के दोनों पक्षों पर कुछ प्रकार्य (गणित) लागू किया जाता है, तो परिणामी समीकरण में इसके समाधानों के बीच प्रारंभिक समीकरण के समाधान होते हैं, लेकिन इसके अतिरिक्त समाधान हो सकते हैं जिन्हें बाहरी समाधान कहा जाता है। उदाहरण के लिए, समीकरण का समाधान है । दोनों पक्षों को 2 के घातांक तक उठाना (जिसका अर्थ है प्रकार्य को लागू करना समीकरण के दोनों ओर) समीकरण को बदल देता है , जिसमें न केवल पिछला समाधान है बल्कि बाहरी समाधान को भी प्रस्तुत करता है, इसके अलावा, यदि प्रकार्य कुछ मानों (जैसे 1/x, जो x = 0 के लिए परिभाषित नहीं है) पर परिभाषित नहीं है, तो उन मानों पर मौजूद समाधान खो सकते हैं। इस प्रकार, इस तरह के परिवर्तन को समीकरण में लागू करते समय सावधानी बरतनी चाहिए।

उपरोक्त परिवर्तन समीकरण हल करने के लिए सबसे प्राथमिक तरीकों का, साथ ही कुछ कम प्राथमिक, जैसे गॉसियन उन्मूलन आधार है।

बीजगणित

बहुपद समीकरण

Main article: बहुपद समीकरण
बहुपद समीकरण x2 – x + 2 = 0 के समाधान -1 और 2 वे बिंदु हैं जहाँ द्विघात फलन y = x2 – x + 2 का लेखाचित्र x-अक्ष को काटता है।

सामान्य तौर पर, एक बीजगणितीय समीकरण या बहुपद समीकरण रूप का एक समीकरण है

, या
[lower-alpha 1]

जहाँ P और Q किसी बीजीय (गणित) में गुणांक वाले बहुपद हैं (जैसे, परिमेय संख्या, वास्तविक संख्या, सम्मिश्र संख्या)। एक बीजगणितीय समीकरण एक चर है यदि इसमें केवल एक चर (गणित) सम्मिलित है। दूसरी ओर, एक बहुपद समीकरण में कई चर सम्मिलित हो सकते हैं, जिस स्थिति में इसे बहुभिन्नरूपी (एकाधिक चर, x, y, z, आदि) कहा जाता है।

उदाहरण के लिए,

पूर्णांक गुणांक और के साथ एक अविभाज्य बीजगणितीय (बहुपद) समीकरण है

परिमेय संख्याओं पर एक बहुभिन्नरूपी बहुपद समीकरण है।

परिमेय संख्या वाले कुछ बहुपद समीकरणों का एक हल होता है जो एक बीजगणितीय व्यंजक होता है, जिसमें केवल उन गुणांकों को सम्मिलित करने वाली संक्रियाओं की परिमित संख्या होती है (अर्थात, बीजगणितीय हल हो सकता है)। यह बहुपद एक, दो, तीन या चार की घात के ऐसे सभी समीकरणों के लिए किया जा सकता है; लेकिन डिग्री पांच या अधिक के समीकरणों को हमेशा इस तरह से हल नहीं किया जा सकता है, जैसा कि एबेल-रफिनी प्रमेय प्रदर्शित करता है।

एक अविभिन्न बीजगणितीय समीकरण (बहुपदों की मूल खोज देखें) और कई बहुभिन्नरूपी बहुपद समीकरणों के सामान्य समाधानों की वास्तविक संख्या या जटिल संख्या समाधानों के कुशलतापूर्वक सटीक अनुमानों की गणना करने के लिए बड़ी मात्रा में अनुसंधान समर्पित किया गया है (बहुपद समीकरणों की प्रणाली देखें) .

रैखिक समीकरणों की प्रणाली

गणितीय कला पर नौ अध्याय, दूसरी शताब्दी की एक अनामक चीनी पुस्तक है जो रेखीय समीकरणों के समाधान की एक विधि का प्रस्ताव करती है।

रैखिक समीकरणों की एक प्रणाली (या रैखिक प्रणाली) एक या अधिक चर (गणित) से जुड़े रैखिक समीकरणों का एक संग्रह है।[lower-alpha 2] उदाहरण के लिए,

तीन चरों में तीन समीकरणों की एक प्रणाली x, y, z है। एक रैखिक प्रणाली का समाधान चर के लिए संख्याओं का एक समनुदेशन है जिससे कि सभी समीकरण एक साथ संतुष्ट हों। उपरोक्त प्रणाली को हल करने वाला एक समीकरण निम्न द्वारा दिया गया है;

क्योंकि यह तीनों समीकरणों को मान्य बनाता है। प्रणाली शब्द इंगित करता है कि समीकरणों को अलग-अलग के स्थान पर सामूहिक रूप से माना जाना चाहिए।

गणित में, रेखीय प्रणालियों का सिद्धांत रेखीय बीजगणित का एक मूलभूत हिस्सा है, एक ऐसा विषय जो आधुनिक गणित के कई भागों में प्रयोग किया जाता है। समाधान खोजने के लिए संगणनात्मक कलन विधि संख्यात्मक रैखिक बीजगणित का एक महत्वपूर्ण हिस्सा हैं, और भौतिकी, अभियांत्रिकी, रसायन विज्ञान, परिकलक विज्ञान और अर्थशास्त्र में एक प्रमुख भूमिका निभाते हैं। गैर-रैखिक समीकरणों की प्रणाली प्रायः एक रैखिक प्रणाली (रैखिकीकरण देखें) द्वारा अनुमानित हो सकती है, एक अपेक्षाकृत जटिल प्रणाली के गणितीय प्रतिरूप या परिकलक अनुकरण बनाते समय एक सहायक तकनीक है।

ज्यामिति

विश्लेषणात्मक ज्यामिति

नीली और लाल रेखा सभी बिंदुओं (x,y) का सम्मुच्चय है जैसे क्रमशः x+y=5 और -x+2y=4। उनका प्रतिच्छेदन (यूक्लिडीय ज्यामिति) बिंदु, (2,3), दोनों समीकरणों को संतुष्ट करता है।
एक शंक्वाकार खंड एक समतल और परिक्रमण के एक शंकु का प्रतिच्छेदन है।

यूक्लिडीय ज्यामिति, स्थल में प्रत्येक बिंदु के लिए निर्देशांक का एक सम्मुच्चय जोड़ना संभव है, उदाहरण के लिए एक आयतीय संजाल द्वारा। यह विधि किसी को ज्यामितीय आकृतियों को समीकरणों द्वारा चिह्नित करने की अनुमति देती है। त्रि-आयामी अंतरिक्ष में एक विमान को फॉर्म के समीकरण के समाधान सम्मुच्चय के रूप में व्यक्त किया जा सकता है। , जहाँ और वास्तविक संख्याएँ हैं और अज्ञात हैं जो आयतीय संजाल द्वारा दी गई प्रणाली में एक बिंदु के निर्देशांक के अनुरूप हैं। मूल्य समीकरण द्वारा परिभाषित समतल के लम्बवत् सदिश के निर्देशांक हैं। एक रेखा को दो समतलों के प्रतिच्छेदन के रूप में व्यक्त किया जाता है, जो कि मानों के साथ एकल रेखीय समीकरण के समाधान सम्मुच्चय के रूप में या मूल्यों के साथ दो रैखिक समीकरणों के समाधान सम्मुच्चय के रूप में होता है।

एक शंकु खंड समीकरण के साथ एक तल शंकु का प्रतिच्छेदन है। दूसरे शब्दों में, स्थल में, सभी शांकवों को तल के समीकरण और अभी दिए गए शंकु के समीकरण के हल समुच्चय के रूप में परिभाषित किया जाता है। यह औपचारिकता किसी को एक शंकु के केंद्रबिन्दु की स्थिति और गुणों को निर्धारित करने की अनुमति देती है।

समीकरणों के उपयोग से ज्यामितीय प्रश्नों को हल करने के लिए गणित के एक बड़े क्षेत्र पर आवाहन करने की अनुमति मिलती है। कार्तीय समन्वय प्रणाली ज्यामितीय समस्या को एक विश्लेषण समस्या में बदल देती है, एक बार जब आंकड़े समीकरणों में परिवर्तित हो जाते हैं तो उनको विश्लेषणात्मक ज्यामिति नाम दिया जाता है। डेसकार्टेस द्वारा उल्लिखित यह दृष्टिकोण, प्राचीन ग्रीक गणितज्ञों द्वारा कल्पना की गई ज्यामिति के प्रकार को समृद्ध और संशोधित करता है।

वर्तमान में, विश्लेषणात्मक ज्यामिति गणित की एक सक्रिय शाखा को निर्दिष्ट करती है। हालांकि यह अभी भी आंकड़ों को चित्रित करने के लिए समीकरणों का उपयोग करता है, यह कार्यात्मक विश्लेषण और रैखिक बीजगणित जैसी अन्य परिष्कृत तकनीकों का भी उपयोग करता है।

कार्तीय समीकरण

कार्तीय समन्वय प्रणाली एक समन्वय प्रणाली है जो प्रत्येक बिंदु (ज्यामिति) को विशिष्ट रूप से एक तल (ज्यामिति) में संख्या निर्देशांक की एक जोड़ी द्वारा निर्दिष्ट करती है, जो कि धनात्मक और ऋणात्मक संख्याएँ हैं, जो लंबाई की एक ही इकाई का उपयोग करके चिह्नित किए गए हैं।

तीन कार्तीय निर्देशांकों के उपयोग से त्रि-आयामी स्थल (गणित) में किसी भी बिंदु की स्थिति निर्दिष्ट करने के लिए एक ही सिद्धांत का उपयोग किया जा सकता है, जो तीन परस्पर लंबवत तल के लिए हस्ताक्षरित दूरी हैं (या, समतुल्य रूप से, इसके लंबवत प्रक्षेपण द्वारा तीन परस्पर लंबवत रेखाओं पर हस्ताक्षरित है)।

लाल रंग में चिह्नित मूल पर केंद्रित त्रिज्या 2 के एक चक्र के साथ कार्टेशियन समन्वय प्रणाली। एक वृत्त का समीकरण (x − a)2 + (y − b)2 = r2 है, जहाँ a और b केंद्र के निर्देशांक हैं (a, b) और R त्रिज्या है।

17 वीं शताब्दी में रेने डेसकार्टेस (लैटिनीकरण (साहित्य) नाम: कार्टेसियस) द्वारा कार्तीय निर्देशांक के आविष्कार ने यूक्लिडियन ज्यामिति और बीजगणित के बीच पहला व्यवस्थित कड़ी प्रदान करके गणित में क्रांति ला दी। कार्तीय समन्वय प्रणाली का उपयोग करते हुए, ज्यामितीय आकृतियों (जैसे घटता) को 'कार्तीय समीकरण' द्वारा वर्णित किया जा सकता है: बीजगणितीय समीकरण जिसमें आकृति पर स्थित बिंदुओं के निर्देशांक सम्मिलित होते हैं। उदाहरण के लिए, एक समतल में त्रिज्या 2 का एक वृत्त, जो एक विशेष बिंदु पर केन्द्रित होता है जिसे मूल कहा जाता है, को उन सभी बिंदुओं के समुच्चय के रूप में वर्णित किया जा सकता है जिनके निर्देशांक x और y समीकरण x2 + y2 = 4 को संतुष्ट करते हैं।

प्राचलिक समीकरण

Main article: प्राचलिक समीकरण

एक वक्र के लिए एक प्राचलिक समीकरण वक्र के बिंदुओं के निर्देशांक को एक चर (गणित) के कार्यों के रूप में व्यक्त करता है, जिसे एक मापदण्ड कहा जाता है।[7][8] उदाहरण के लिए,

एकक वृत्त के लिए प्राचलिक समीकरण हैं, जहां t मापदण्ड है। साथ में, इन समीकरणों को वक्र का 'प्राचलिक प्रतिनिधित्व' कहा जाता है।

प्राचलिक समीकरण की धारणा को सतह (सांस्थिति), बहुआयामी और उच्च आयाम के बीजगणितीय विविधता के लिए सामान्यीकृत किया गया है, जिसमें बहुरूपता या विविधता के आयाम के बराबर मापदंडों की संख्या और समीकरणों की संख्या के बराबर है। उस स्थान का आयाम जिसमें बहुरूपता या विविधता पर विचार किया जाता है (वक्र के लिए आयाम एक है और सतहों के आयाम दो और दो मापदण्ड आदि के लिए एक मापदण्ड का उपयोग किया जाता है)।

संख्या सिद्धांत

डायोफैंटाइन समीकरण

Main article: डायोफैंटाइन समीकरण

एक डायोफैंटाइन समीकरण दो या दो से अधिक अज्ञात में एक बहुपद समीकरण है जिसके लिए केवल पूर्णांक समाधान मांगे जाते हैं (एक पूर्णांक समाधान ऐसा समाधान है कि सभी अज्ञात पूर्णांक मान लेते हैं)। एक रेखीय डायोफैंटाइन समीकरण एक बहुपद शून्य या एक की डिग्री के दो योगों के बीच का समीकरण है। रेखीय डायोफैंटाइन समीकरण का एक उदाहरण ax + by = c है, जहाँ a, b और c स्थिरांक हैं। एक 'घातीय डायोफैंटाइन समीकरण' वह है जिसके लिए समीकरण की शर्तों के प्रतिपादक अज्ञात हो सकते हैं।

'डायोफैंटाइन समस्याओं' में अज्ञात चरों की तुलना में कम समीकरण होते हैं और इसमें सभी समीकरणों के लिए सही ढंग से काम करने वाले पूर्णांकों को खोजना सम्मिलित होता है। अधिक तकनीकी भाषा में, वे एक बीजगणितीय वक्र, बीजगणितीय सतह, या अधिक सामान्य वस्तु को परिभाषित करते हैं, और उस पर जालक बिंदुओं के बारे में पूछते हैं।

डायोफैंटाइन शब्द तीसरी शताब्दी के हेलेनिस्टिक गणितज्ञ, अलेक्जेंड्रिया के डायोफैंटस को संदर्भित करता है, जिन्होंने इस तरह के समीकरणों का अध्ययन किया और बीजगणित में प्रतीकवाद को प्रस्तुत करने वाले पहले गणितज्ञों में से एक थे।। डायोफैंटाइन समस्याओं का गणितीय अध्ययन जिसे डायोफैंटस ने शुरू किया था, उसे अब 'डायोफैंटाइन विश्लेषण' कहा जाता है।

बीजगणितीय और पारलौकिक संख्याएं

Main articles: बीजगणितीय संख्या and पारलौकिक संख्या

बीजगणितीय संख्या एक संख्या है जो परिमेय संख्या गुणांकों के साथ चर में एक गैर-शून्य बहुपद समीकरण का एक समाधान है (या समतुल्य - समाशोधन हर द्वारा - पूर्णांक गुणांक के साथ)। π जैसी संख्याएँ जो बीजगणितीय नहीं हैं, उन्हें पारलौकिक कहा जाता है। लगभग सभी वास्तविक और सम्मिश्र संख्याएँ पारलौकिक हैं।

बीजगणितीय ज्यामिति

Main article: बीजगणितीय ज्यामिति

बीजगणितीय ज्यामिति गणित की एक शाखा है, जो शास्त्रीय रूप से बहुपद समीकरणों के समाधान का अध्ययन करती है। आधुनिक बीजगणितीय ज्यामिति भाषा और ज्यामिति की समस्याओं के साथ अमूर्त बीजगणित की अधिक अमूर्त तकनीकों, विशेष रूप से क्रमविनिमेय बीजगणित पर आधारित है।

बीजगणितीय ज्यामिति में अध्ययन की मूलभूत वस्तुएँ बीजगणितीय विविधता हैं, जो बहुपद समीकरणों के प्रणाली के समाधान सम्मुच्चय की ज्यामितीय अभिव्यक्तियाँ हैं। बीजगणितीय किस्मों के सबसे अधिक अध्ययन किए गए वर्गों के उदाहरण हैं: समतल बीजगणितीय वक्र, जिसमें रेखाएँ, वृत्त, परवलय, दीर्घवृत्त, अतिपरवलय, घनीय वक्र जैसे अण्डाकार वक्र और क्वार्टिक वक्र जैसे लेम्निस्केट्स और कैसिनी अंडाकार सम्मिलित हैं। यदि इसके निर्देशांक दिए गए बहुपद समीकरण को संतुष्ट करते हैं तो समतल का एक बिंदु एक बीजगणितीय वक्र से संबंधित होता है। मूल प्रश्नों में वक्र के एकवचन बिंदु, विभक्ति बिंदु और अनंत पर बिंदु जैसे विशेष रुचि के बिंदुओं का अध्ययन सम्मिलित है। अधिक उन्नत प्रश्नों में वक्र की सांस्थिति और विभिन्न समीकरणों द्वारा दिए गए वक्रों के बीच संबंध सम्मिलित होते हैं।

विभेदक समीकरण

Main article: विभेदक समीकरण
एक असामान्य आकर्षण, जो एक निश्चित अंतर समीकरण को हल करते समय उत्पन्न होता है

अवकल समीकरण एक गणित का समीकरण है जो कुछ फलनों (गणित) को उसके अवकलजों से संबंधित करता है। अनुप्रयोगों में, कार्य सामान्यतः भौतिक मात्रा का प्रतिनिधित्व करते हैं, यौगिक परिवर्तन की अपनी दरों का प्रतिनिधित्व करते हैं, और समीकरण दोनों के बीच संबंध को परिभाषित करता है। क्योंकि इस तरह के संबंध अत्यंत सामान्य हैं, भौतिक विज्ञान, अभियान्त्रिकी, अर्थशास्त्र और जीव विज्ञान सहित कई विषयों में अवकल समीकरण प्रमुख भूमिका निभाते हैं।

शुद्ध गणित में, अंतर समीकरणों का कई अलग-अलग दृष्टिकोणों से अध्ययन किया जाता है, जो अधिकतर उनके समीकरण को संतुष्ट करने वाले कार्यों के सम्मुच्चय से संबंधित होते हैं। स्पष्ट सूत्रों द्वारा केवल सबसे सरल अवकल समीकरणों को हल किया जा सकता है; हालाँकि, किसी दिए गए अवकल समीकरण के समाधान के कुछ गुण उनके सटीक रूप को खोजे बिना निर्धारित किए जा सकते हैं।

यदि समाधान के लिए स्व-निहित सूत्र उपलब्ध नहीं है, तो परिकलक का उपयोग करके समाधान को संख्यात्मक रूप से अनुमानित किया जा सकता है। गतिशील प्रणालियों का सिद्धांत अंतर समीकरणों द्वारा वर्णित प्रणालियों के गुणात्मक विश्लेषण पर जोर देता है, जबकि सटीकता की एक निश्चित डिग्री के साथ समाधान निर्धारित करने के लिए कई संख्यात्मक तरीके विकसित किए गए हैं।

साधारण अंतर समीकरण

Main article: साधारण विभेदक समीकरण

साधारण अंतर समीकरण या ODE एक समीकरण है जिसमें स्वतंत्र चर और उसके व्युत्पादित का एक कार्य होता है। साधारण शब्द का प्रयोग आंशिक अंतर समीकरण के विपरीत किया जाता है, जो एक स्वतंत्र चर से अधिक के संबंध में हो सकता है।

रेखीय अवकल समीकरण, जिनके ऐसे हल हैं जिन्हें गुणांकों द्वारा जोड़ा और गुणा किया जा सकता है, अच्छी तरह से परिभाषित और समझा जाता है, और सटीक बंद-रूप समाधान प्राप्त होते हैं। इसके विपरीत, ODE जिनमें योगात्मक समाधानों की कमी होती है, अरैखिक होते हैं, और उन्हें हल करना कहीं अधिक जटिल होता है, क्योंकि बंद रूप में प्राथमिक कार्यों द्वारा शायद ही कभी उनका प्रतिनिधित्व किया जा सकता है: इसके बजाय, ODE के सटीक और विश्लेषणात्मक समाधान श्रृंखला या अभिन्न रूप में होते हैं। हाथ से या परिकलक द्वारा लागू आलेखीय और संख्यात्मक साधारण अंतर समीकरण पद्धति, ODE के समाधान का अनुमान लगा सकते हैं और शायद उपयोगी जानकारी प्राप्त कर सकते हैं, जो प्रायः सटीक, विश्लेषणात्मक समाधान के अभाव में पर्याप्त होती है।

आंशिक अंतर समीकरण

Main article: आंशिक अंतर समीकरण

एक आंशिक अंतर समीकरण (PDE) एक अंतर समीकरण है जिसमें अज्ञात बहुभिन्नरूपी कलन और उनके आंशिक व्युत्पादित सम्मिलित हैं। (यह सामान्य अंतर समीकरणों के विपरीत है, जो एक चर और उनके व्युत्पादित के कार्यों से निपटते हैं।) PDE का उपयोग कई चर के कार्यों से जुड़ी समस्याओं को तैयार करने के लिए किया जाता है, और या तो हाथ से हल किया जाता है, या एक प्रासंगिक परिकलक प्रतिरूप बनाने के लिए उपयोग किया जाता है। .

PDE का उपयोग विभिन्न प्रकार की घटनाओं जैसे ध्वनि, गर्मी, स्थिर विद्युतिकी, बिजली का गतिविज्ञान, द्रव प्रवाह, लोच (भौतिकी), या परिमाण यांत्रिकी का वर्णन करने के लिए किया जा सकता है। PDE के संदर्भ में समान रूप से अलग-अलग भौतिक घटनाओं को औपचारिक रूप दिया जा सकता है। जिस तरह साधारण अंतर समीकरण प्रायः एक-आयामी गतिशील प्रणालियों का प्रतिरूप करते हैं, आंशिक अंतर समीकरण प्रायः बहुआयामी प्रणालियों का प्रतिरूप करते हैं। PDE अपने सामान्यीकरण को प्रसंभाव्य आंशिक अंतर समीकरणों में पाते हैं।

समीकरणों के प्रकार

समीकरणों को संक्रिया के प्रकार (गणित) और सम्मिलित मात्राओं के अनुसार वर्गीकृत किया जा सकता है। महत्वपूर्ण प्रकारों में सम्मिलित हैं:

  • एक बीजगणितीय समीकरण या बहुपद समीकरण एक समीकरण है जिसमें दोनों पक्ष बहुपद होते हैं बहुपद समीकरणों की प्रणाली भी देखें)। इन्हें बहुपद की डिग्री द्वारा आगे वर्गीकृत किया गया है:
  • एक डायोफैंटाइन समीकरण एक समीकरण है जहां अज्ञात को पूर्णांक होना आवश्यक है
  • एक अनुभवातीत समीकरण एक ऐसा समीकरण है जिसमें इसके अज्ञात का एक पारलौकिक समीकरण सम्मिलित है
  • प्राचलिक समीकरण एक ऐसा समीकरण है जिसमें चरों के समाधान को कुछ अन्य चरों के कार्यों के रूप में व्यक्त किया जाता है, जिन्हें समीकरणों में प्रदर्शित होने वाले मापदण्ड कहा जाता है
  • एक कार्यात्मक समीकरण एक ऐसा
  • समीकरण है जिसमें अज्ञात सामान्य मात्रा के बजाय कार्य (गणित) हैं
  • व्युत्पादित, संपूर्ण और परिमित अंतर वाले समीकरण:
    • एक अंतर समीकरण एक कार्यात्मक समीकरण है जिसमें अज्ञात कार्यों के व्युत्पादित सम्मिलित होते हैं, जहां प्रकार्य और उसके व्युत्पादित का मूल्यांकन एक ही बिंदु पर किया जाता है, जैसे कि . अवकल समीकरणों को एकल चर वाले फलनों के लिए सामान्य अवकल समीकरणों और अनेक चरों वाले फलनों के लिए आंशिक अवकल समीकरणों में उप-विभाजित किया जाता है।
    • एक अभिन्न समीकरण एक कार्यात्मक समीकरण है जिसमें अज्ञात कार्यों के प्रतिपक्षी सम्मिलित हैं। चर के कार्यों के लिए, ऐसा समीकरण एक अंतर समीकरण से भिन्न होता है, मुख्य रूप से इसके व्युत्पन्न द्वारा प्रकार्य को प्रतिस्थापित करने वाले चर के परिवर्तन के माध्यम से, हालांकि यह मामला नहीं है जब अभिन्न एक खुली सतह पर लिया जाता है
    • एक पूर्णांक-अंतर समीकरण एक कार्यात्मक समीकरण है जिसमें अज्ञात कार्यों के व्युत्पादित और एंटीडेरिवेटिव दोनों सम्मिलित हैं। एक चर के कार्यों के लिए, ऐसा समीकरण चर के समान परिवर्तन के माध्यम से अभिन्न और अंतर समीकरणों से भिन्न होता है।
    • देरी अंतर समीकरण का एक कार्यात्मक अंतर समीकरण एक प्रकार्य समीकरण है जिसमें अज्ञात कार्यों के व्युत्पादित सम्मिलित हैं, जिनका मूल्यांकन कई बिंदुओं पर किया जाता है, जैसे
    • एक अंतर समीकरण एक समीकरण है जहां अज्ञात एक फलन f है जो समीकरण में f(x), f(x−1), ..., f(x−k) के माध्यम से होता है, कुछ पूर्ण पूर्णांक k के लिए कहा जाता है समीकरण का क्रम। यदि x को एक पूर्णांक के रूप में प्रतिबंधित किया जाता है, तो एक अंतर समीकरण पुनरावृत्ति संबंध के समान होता है
    • एक स्टोचैस्टिक अंतर समीकरण एक अंतरात्मक समीकरण है जिसमें एक या अधिक शब्द एक प्रसंभाव्य प्रक्रिया है

यह भी देखें


टिप्पणियाँ

  1. ↑ As such an equation can be rewritten P – Q = 0, many authors do not consider this case explicitly.
  2. ↑ The subject of this article is basic in mathematics, and is treated in a lot of textbooks. Among them, Lay 2005, Meyer 2001, and Strang 2005 contain the material of this article.


संदर्भ

  1. ↑ 1.0 1.1 Recorde, Robert, The Whetstone of Witte ... (London, England: Jhon Kyngstone, 1557), the third page of the chapter "The rule of equation, commonly called Algebers Rule."
  2. ↑ 2.0 2.1 "समीकरण - गणित खुला संदर्भ". www.mathopenref.com. Retrieved 2020-09-01.
  3. ↑ "समीकरण और सूत्र". www.mathsisfun.com. Retrieved 2020-09-01.
  4. ↑ Marcus, Solomon; Watt, Stephen M. "एक समीकरण क्या है?". Retrieved 2019-02-27.
  5. ↑ Lachaud, Gilles. "Équation, mathématique". यूनिवर्सल एनसाइक्लोपीडिया (in français).
  6. ↑ "A statement of equality between two expressions. Equations are of two types, identities and conditional equations (or usually simply "equations")". « Equation », in Mathematics Dictionary, Glenn James [de] et Robert C. James (éd.), Van Nostrand, 1968, 3 ed. 1st ed. 1948, p. 131.
  7. ↑ Thomas, George B., and Finney, Ross L., Calculus and Analytic Geometry, Addison Wesley Publishing Co., fifth edition, 1979, p. 91.
  8. ↑ Weisstein, Eric W. "Parametric Equations." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/ParametricEquations.html


बाहरी कड़ियाँ

  • Winplot: General Purpose plotter that can draw and animate 2D and 3D mathematical equations.
  • Equation plotter: A web page for producing and downloading pdf or postscript plots of the solution sets to equations and inequations in two variables (x and y).

श्रेणी: प्रारंभिक बीजगणित

Retrieved from "https://alpha.indicwiki.in/index.php?title=समीकरण&oldid=77351"