समीकरण

For other uses, see समीकरण (disambiguation).

आधुनिक अंकन में 14x + 15 = 71 के समतुल्य एक बराबर चिह्न का पहला उपयोग। वेल्स के रॉबर्ट रिकॉर्डे द्वारा विट्टे का वेटस्टोन से (1557)।

गणित में, एक समीकरण एक सूत्र है जो दो व्यंजकों (गणित) की समानता (गणित) को बराबर के चिह्न = से जोड़कर व्यक्त करता है। अन्य भाषाओं में शब्द समीकरण और इसके सजातीय अर्थों में सूक्ष्म रूप से भिन्न अर्थ हो सकते हैं; उदाहरण के लिए, फ्रांसीसी भाषा में एक समीकरण को एक या एक से अधिक चर (गणित) के रूप में परिभाषित किया जाता है, जबकि अंग्रेजी भाषा में, बराबर चिह्न से संबंधित दो अभिव्यक्तियों से युक्त कोई भी अच्छी तरह से तैयार सूत्र एक समीकरण है।

चर वाले समीकरण को हल करने में यह निर्धारित करना सम्मिलित है कि चर के कौन से मान समानता को सत्य बनाते हैं। वे चर जिनके लिए समीकरण को हल करना होता है, 'अज्ञात' भी कहलाते हैं, और अज्ञात के वे मान जो समानता को संतुष्ट करते हैं, समीकरण के हल (समीकरण) कहलाते हैं। समीकरण दो प्रकार के होते हैं: सर्वसमिका (गणित) और सशर्त समीकरण। चर के सभी मूल्यों के लिए एक सर्वसमिका सत्य है। सशर्त समीकरण केवल चरों के विशेष मानों के लिए सत्य होता है।

एक समीकरण को दो व्यंजकों (गणित) के रूप में लिखा जाता है, जो बराबर चिह्न (=) से जुड़ा होता है। बराबर के चिह्न वाले समीकरण के दोनों पक्षों के व्यंजक समीकरण के बाएँ पक्ष और दाएँ पक्ष कहलाते हैं। बहुत बार किसी समीकरण के दाहिने पक्ष को शून्य मान लिया जाता है। यह मानने से व्यापकता कम नहीं होती है, क्योंकि इसे दोनों पक्षों से दाहिनी ओर घटाकर महसूस किया जा सकता है।

सबसे सामान्य प्रकार का समीकरण एक [[बहुपद समीकरण]] है (सामान्यतः इसे बीजगणितीय समीकरण भी कहा जाता है) जिसमें दो पक्ष बहुपद होते हैं। एक बहुपद समीकरण के पक्षों में एक या एक से अधिक योग संकेत और शब्दावली होती है। उदाहरण के लिए, समीकरण

$Ax^{2}+Bx+C-y=0$

बाईं ओर $Ax^{2}+Bx+C-y$ है, जिसमें चार पद हैं, और दाहिनी ओर, केवल एक शब्द से मिलकर $0$ है। चर (गणित) के नाम बताते हैं कि x और y अज्ञात हैं, और वह A, B, और C मापदण्ड हैं, लेकिन यह सामान्य रूप से संदर्भ द्वारा तय किया जाता है (कुछ संदर्भों में, y एक मापदण्ड हो सकता है, या A, B, और C साधारण चर हो सकते हैं)।

एक समीकरण उस पैमाने के अनुरूप होता है जिसमें वजन रखा जाता है। जब किसी चीज़ के बराबर वज़न (जैसे, अनाज) को दो पलड़ों में रखा जाता है, तो दो वज़न तराजू को संतुलन में रखते हैं और उन्हें बराबर कहा जाता है। यदि पलड़े के एक पलड़े में से अन्न की गिनती निकाली जाए, तो पलड़े को सन्तुलित रखने के लिथे दूसरे पलड़े में से भी उतना ही अन्न निकाला जाए। अधिक सामान्यतः, एक समीकरण संतुलन में रहता है यदि इसके दोनों पक्षों पर एक ही संचालन किया जाता है।

कार्तीय ज्यामिति में, ज्यामितीय आकृतियों का वर्णन करने के लिए समीकरणों का उपयोग किया जाता है। जैसा कि जिन समीकरणों पर विचार किया जाता है, जैसे निहित समीकरण या प्राचलिक समीकरण, के असीम रूप से कई समाधान होते हैं, उद्देश्य अब अलग है: समाधानों को स्पष्ट रूप से देने या उन्हें गिनने के बजाय, जो असंभव है, आंकड़ों के गुणों का अध्ययन करने के लिए समीकरणों का उपयोग किया जाता है। यह बीजगणितीय ज्यामिति का प्रारंभिक विचार है, जो गणित का एक महत्वपूर्ण क्षेत्र है।

बीजगणित समीकरणों के दो मुख्य परिवारों का अध्ययन करता है: बहुपद समीकरण और उनमें से, रैखिक समीकरणों का विशेष मामला। चूंकि जिन समीकरणों पर विचार किया जाता है, जैसे अंतर्निहित समीकरण या प्राचलिक समीकरण, उनके असीम रूप से कई समाधान होते हैं, उद्देश्य अब अलग है: समाधानों को स्पष्ट रूप से देने या उन्हें गिनने के बजाय, जो असंभव है, आंकड़ों के गुणों का अध्ययन करने के लिए समीकरणों का उपयोग किया जाता है। बीजगणित डायोफैंटाइन समीकरणों का भी अध्ययन करता है जहां गुणांक और समाधान पूर्णांक होते हैं। उपयोग की जाने वाली तकनीकें भिन्न हैं और संख्या सिद्धांत से आती हैं। ये समीकरण सामान्य तौर पर कठिन होते हैं; कोई प्रायः समाधान के अस्तित्व या अनुपस्थिति को खोजने के लिए खोज करता है, और यदि वे मौजूद हैं, तो समाधानों की संख्या गिनने के लिए मौजूद हैं।

विभेदक समीकरण ऐसे समीकरण होते हैं जिनमें एक या अधिक कार्य और उनके व्युत्पादित सम्मिलित होते हैं। वे उस फलन के लिए एक व्यंजक खोज कर हल किए जाते हैं जिसमें अवकलज सम्मिलित नहीं है। विभेदक समीकरणों का उपयोग प्रतिरूप प्रक्रियाओं के लिए किया जाता है जिसमें चर के परिवर्तन की दर सम्मिलित होती है, और भौतिकी, रसायन विज्ञान, जीव विज्ञान और अर्थशास्त्र जैसे क्षेत्रों में उपयोग किया जाता है।

= प्रतीक, जो हर समीकरण में प्रकट होता है, का आविष्कार 1557 में रॉबर्ट रिकॉर्डे द्वारा किया गया था, जिन्होंने माना था कि समान लंबाई वाली समानांतर सीधी रेखाओं से अधिक समान कुछ भी नहीं हो सकता है।

परिचय

अनुरूप चित्रण

एक साधारण समीकरण का चित्रण; x, y, z वास्तविक संख्याएँ हैं, जो वज़न के समान हैं।

एक समीकरण एक वजनी पैमाने, तराजू या झूले के समान होता है।

समीकरण का प्रत्येक पक्ष संतुलन के एक पक्ष से मेल खाता है। प्रत्येक पक्ष पर अलग-अलग मात्राएँ रखी जा सकती हैं: यदि दोनों पक्षों पर भार समान हैं, तो तराजू संतुलित करता है, और सादृश्यता में, संतुलन का प्रतिनिधित्व करने वाली समानता भी संतुलित होती है (यदि नहीं, तो संतुलन की कमी एक असमानता से मेल खाती है ( गणित) एक असमिका द्वारा दर्शाया गया है)।

उदाहरण में, x, y और z सभी अलग-अलग मात्राएँ हैं (इस मामले में वास्तविक संख्याएँ) जिन्हें गोलाकार भार के रूप में दर्शाया गया है, और x, y और z में से प्रत्येक का अलग-अलग वज़न है। योग वजन जोड़ने के अनुरूप है, जबकि घटाव पहले से मौजूद वजन को हटाने से मेल खाता है। जब समानता धारण करती है, तो प्रत्येक पक्ष का कुल भार समान होता है।

मापदण्ड एवं अपरिचित

See also: अभिव्यक्ति (गणित)

समीकरणों में प्रायः अज्ञात के अतिरिक्त अन्य पद होते हैं। ये अन्य शब्द, जिन्हें ज्ञात माना जाता है, सामान्यतः स्थिरांक, गुणांक या मापदण्ड कहलाते हैं।

x और y को अज्ञात के रूप में सम्मिलित करने वाले समीकरण का एक उदाहरण और मापदण्ड R है

$x^{2}+y^{2}=R^{2}.$

जब R को 2 (R = 2) के मान के लिए चुना जाता है, तो इस समीकरण को कार्तीय निर्देशांक में मूल के चारों ओर 2 के त्रिज्या के चक्र के समीकरण के रूप में सर्वसमिकाा जाएगा। इसलिए, R अनिर्दिष्ट के साथ समीकरण चक्र के लिए सामान्य समीकरण है।

सामान्यतः, अज्ञात को वर्णमाला के अंत में अक्षरों द्वारा दर्शाया जाता है, x, y, z, w, ..., जबकि गुणांक (मापदण्ड) शुरुआत में अक्षरों द्वारा दर्शाए जाते हैं, a, b, c, d, .. ... उदाहरण के लिए, सामान्य द्विघात समीकरण को सामान्यतः ax²+ bx+ c = 0 लिखा जाता है.

समाधान खोजने की प्रक्रिया, या, मापदंडों के मामले में, अज्ञात को मापदंडों के संदर्भ में व्यक्त करना, समीकरण हल करना कहलाता है। मापदंडों के संदर्भ में समाधानों की ऐसी अभिव्यक्तियाँ भी समाधान कहलाती हैं।

समीकरणों की एक प्रणाली एक साथ समीकरणों का एक सम्मुच्चय है, सामान्यतः कई अविदित में जिसके लिए सामान्य समाधान मांगे जाते हैं। इस प्रकार, प्रणाली का समाधान प्रत्येक अज्ञात के लिए मूल्यों का एक सम्मुच्चय है, जो एक साथ प्रणाली में प्रत्येक समीकरण का समाधान बनाते हैं। उदाहरण के लिए, प्रणाली

${\begin{aligned}3x+5y&=2\\5x+8y&=3\end{aligned}}$

अद्वितीय समाधान x= −1, y=1 है।

सर्वसमिका

Main articles: सर्वसमिका (गणित) and त्रिकोणमितीय सर्वसमिकाओं की सूची

एक सर्वसमिका एक समीकरण है जो इसमें निहित चर(नों) के सभी संभावित मानों के लिए सत्य है। बीजगणित और कलन में अनेक सर्वसमिकाएँ ज्ञात हैं। एक समीकरण को हल करने की प्रक्रिया में, एक समीकरण को सरल बनाने के लिए प्रायः एक सर्वसमिका का उपयोग किया जाता है, जिससे इसे अधिक आसानी से हल किया जा सकता है।

बीजगणित में, एक सर्वसमिका का उदाहरण दो वर्गों का अंतर है:

$x^{2}-y^{2}=(x+y)(x-y)$

जो सभी x और y के लिए सत्य है।

त्रिकोणमिति एक ऐसा क्षेत्र है जहां कई सर्वसमिका मौजूद हैं; ये त्रिकोणमितीय समीकरणों में हेरफेर करने या हल करने में उपयोगी होते हैं। कई में से दो जिनमें द्विज्या और कोटिज्या प्रकार्य सम्मिलित हैं:

$\sin ^{2}(\theta )+\cos ^{2}(\theta )=1$

और

$\sin(2\theta )=2\sin(\theta )\cos(\theta )$

जो θ के सभी मानों के लिए सत्य हैं।

उदाहरण के लिए, समीकरण को संतुष्ट करने वाले θ के मान को हल करने के लिए:

$3\sin(\theta )\cos(\theta )=1\,,$

जहां θ 0 और 45 डिग्री के बीच सीमित है, कोई उत्पाद देने के लिए उपरोक्त सर्वसमिका का उपयोग कर सकता है:

${\frac {3}{2}}\sin(2\theta )=1\,,$

θ के लिए निम्नलिखित समाधान प्राप्त करना:

$\theta ={\frac {1}{2}}\arcsin \left({\frac {2}{3}}\right)\approx 20.9^{\circ }.$

चूँकि ज्या फलन एक आवर्ती फलन है, यदि θ पर कोई प्रतिबंध नहीं है तो इसके अपरिमित रूप से अनेक समाधान हैं। इस उदाहरण में, θ को 0 और 45 डिग्री के बीच सीमित करने से समाधान केवल एक संख्या तक सीमित हो जाएगा।

गुण

दो समीकरण या समीकरणों की दो प्रणालियाँ समतुल्य होती हैं, यदि उनके हलों का एक ही समुच्चय हो। निम्नलिखित संक्रियाएँ एक समीकरण या समीकरणों की एक प्रणाली को एक समतुल्य में बदल देती हैं - बशर्ते कि संक्रियाएँ उन व्यंजकों के लिए सार्थक हों जिन पर वे लागू होते हैं:

• किसी समीकरण के दोनों पक्षों में समान मात्रा को जोड़ना या घटाना। इससे पता चलता है कि प्रत्येक समीकरण उस समीकरण के तुल्य होता है जिसमें दाहिनी ओर शून्य होता है।
• एक समीकरण के दोनों पक्षों को एक गैर-शून्य मात्रा से गुणा या विभाजित करना।
• समीकरण के एक पक्ष को बदलने के लिए एक सर्वसमिका (गणित) लागू करना। उदाहरण के लिए, बहुपद विस्तार एक उत्पाद या बहुपदों का गुणन योग है।
• एक प्रणाली के लिए एक समीकरण के दोनों पक्षों में दूसरे समीकरण के संबंधित पक्ष को जोड़कर, समान मात्रा से गुणा किया जाता है।

यदि किसी समीकरण के दोनों पक्षों पर कुछ प्रकार्य (गणित) लागू किया जाता है, तो परिणामी समीकरण में इसके समाधानों के बीच प्रारंभिक समीकरण के समाधान होते हैं, लेकिन इसके अतिरिक्त समाधान हो सकते हैं जिन्हें बाहरी समाधान कहा जाता है। उदाहरण के लिए, समीकरण $x=1$ का समाधान है $x=1$। दोनों पक्षों को 2 के घातांक तक उठाना (जिसका अर्थ है प्रकार्य को लागू करना $f(s)=s^{2}$ समीकरण के दोनों ओर) $x^{2}=1$ समीकरण को बदल देता है , जिसमें न केवल पिछला समाधान है बल्कि बाहरी समाधान $x=-1$ को भी प्रस्तुत करता है, इसके अलावा, यदि प्रकार्य कुछ मानों (जैसे 1/x, जो x = 0 के लिए परिभाषित नहीं है) पर परिभाषित नहीं है, तो उन मानों पर मौजूद समाधान खो सकते हैं। इस प्रकार, इस तरह के परिवर्तन को समीकरण में लागू करते समय सावधानी बरतनी चाहिए।

उपरोक्त परिवर्तन समीकरण हल करने के लिए सबसे प्राथमिक तरीकों का, साथ ही कुछ कम प्राथमिक, जैसे गॉसियन उन्मूलन आधार है।

बीजगणित

बहुपद समीकरण

Main article: बहुपद समीकरण

बहुपद समीकरण के समाधान -1 और 2 x² – x + 2 = 0 वे बिंदु हैं जहाँ द्विघात फलन के फलन का ग्राफ है y = x² – x + 2 x-अक्ष को काटता है।

सामान्य तौर पर, एक बीजगणितीय समीकरण या बहुपद समीकरण रूप का एक समीकरण है

$P=0$, या

$P=Q$

जहाँ P और Q किसी बीजीय (गणित) में गुणांक वाले बहुपद हैं (जैसे, परिमेय संख्या, वास्तविक संख्या, सम्मिश्र संख्या)। एक बीजगणितीय समीकरण एक चर है यदि इसमें केवल एक चर (गणित) सम्मिलित है। दूसरी ओर, एक बहुपद समीकरण में कई चर सम्मिलित हो सकते हैं, जिस स्थिति में इसे बहुभिन्नरूपी (एकाधिक चर, x, y, z, आदि) कहा जाता है।

उदाहरण के लिए,

$x^{5}-3x+1=0$

पूर्णांक गुणांक और के साथ एक अविभाज्य बीजगणितीय (बहुपद) समीकरण है

$y^{4}+{\frac {xy}{2}}={\frac {x^{3}}{3}}-xy^{2}+y^{2}-{\frac {1}{7}}$

परिमेय संख्याओं पर एक बहुभिन्नरूपी बहुपद समीकरण है।

परिमेय संख्या वाले कुछ बहुपद समीकरणों का एक हल होता है जो एक बीजगणितीय व्यंजक होता है, जिसमें केवल उन गुणांकों को सम्मिलित करने वाली संक्रियाओं की परिमित संख्या होती है (अर्थात, बीजगणितीय हल हो सकता है)। यह बहुपद एक, दो, तीन या चार की घात के ऐसे सभी समीकरणों के लिए किया जा सकता है; लेकिन डिग्री पांच या अधिक के समीकरणों को हमेशा इस तरह से हल नहीं किया जा सकता है, जैसा कि एबेल-रफिनी प्रमेय प्रदर्शित करता है।

एक अविभिन्न बीजगणितीय समीकरण (बहुपदों की मूल खोज देखें) और कई बहुभिन्नरूपी बहुपद समीकरणों के सामान्य समाधानों की वास्तविक संख्या या जटिल संख्या समाधानों के कुशलतापूर्वक सटीक अनुमानों की गणना करने के लिए बड़ी मात्रा में अनुसंधान समर्पित किया गया है (बहुपद समीकरणों की प्रणाली देखें) .

रैखिक समीकरणों की प्रणाली

गणितीय कला पर नौ अध्याय, दूसरी शताब्दी की एक अनाम चीनी पुस्तक है जो रेखीय समीकरणों के समाधान की एक विधि का प्रस्ताव करती है।

रैखिक समीकरणों की एक प्रणाली (या रैखिक प्रणाली) एक या अधिक चर (गणित) से जुड़े रैखिक समीकरणों का एक संग्रह है। उदाहरण के लिए,

${\begin{alignedat}{7}3x&&\;+\;&&2y&&\;-\;&&z&&\;=\;&&1&\\2x&&\;-\;&&2y&&\;+\;&&4z&&\;=\;&&-2&\\-x&&\;+\;&&{\tfrac {1}{2}}y&&\;-\;&&z&&\;=\;&&0&\end{alignedat}}$

तीन चरों में तीन समीकरणों की एक प्रणाली x, y, z है। एक रैखिक प्रणाली का समाधान चर के लिए संख्याओं का एक समनुदेशन है जिससे कि सभी समीकरण एक साथ संतुष्ट हों। उपरोक्त प्रणाली को हल करने वाला एक समीकरण निम्न द्वारा दिया गया है;

${\begin{alignedat}{2}x&\,=\,&1\\y&\,=\,&-2\\z&\,=\,&-2\end{alignedat}}$

क्योंकि यह तीनों समीकरणों को मान्य बनाता है। प्रणाली शब्द इंगित करता है कि समीकरणों को अलग-अलग के स्थान पर सामूहिक रूप से माना जाना चाहिए।

गणित में, रेखीय प्रणालियों का सिद्धांत रेखीय बीजगणित का एक मूलभूत हिस्सा है, एक ऐसा विषय जो आधुनिक गणित के कई भागों में प्रयोग किया जाता है। समाधान खोजने के लिए संगणनात्मक कलन विधि संख्यात्मक रैखिक बीजगणित का एक महत्वपूर्ण हिस्सा हैं, और भौतिकी, अभियांत्रिकी, रसायन विज्ञान, परिकलक विज्ञान और अर्थशास्त्र में एक प्रमुख भूमिका निभाते हैं। गैर-रैखिक समीकरणों की प्रणाली प्रायः एक रैखिक प्रणाली (रैखिकीकरण देखें) द्वारा अनुमानित हो सकती है, एक अपेक्षाकृत जटिल प्रणाली के गणितीय प्रतिरूप या परिकलक अनुकरण बनाते समय एक सहायक तकनीक है।

ज्यामिति

विश्लेषणात्मक ज्यामिति

नीली और लाल रेखा सभी बिंदुओं (x,y) का सम्मुच्चय है जैसे x+y=5 और -x+2y=4, क्रमशः। उनका चौराहा (यूक्लिडियन ज्यामिति) बिंदु, (2,3), दोनों समीकरणों को संतुष्ट करता है।

एक शंक्वाकार खंड एक समतल और क्रांति के एक शंकु का प्रतिच्छेदन है।

यूक्लिडीय ज्यामिति, स्थल में प्रत्येक बिंदु के लिए निर्देशांक का एक सम्मुच्चय जोड़ना संभव है, उदाहरण के लिए एक आयतीय संजाल द्वारा। यह विधि किसी को ज्यामितीय आकृतियों को समीकरणों द्वारा चिह्नित करने की अनुमति देती है। त्रि-आयामी अंतरिक्ष में एक विमान को फॉर्म के समीकरण के समाधान सम्मुच्चय के रूप में व्यक्त किया जा सकता है। $ax+by+cz+d=0$, जहाँ $a,b,c$ और $d$ वास्तविक संख्याएँ हैं और $x,y,z$ अज्ञात हैं जो आयतीय संजाल द्वारा दी गई प्रणाली में एक बिंदु के निर्देशांक के अनुरूप हैं। मूल्य $a,b,c$ समीकरण द्वारा परिभाषित समतल के लम्बवत् सदिश के निर्देशांक हैं। एक रेखा को दो समतलों के प्रतिच्छेदन के रूप में व्यक्त किया जाता है, जो कि मानों के साथ एकल रेखीय समीकरण के समाधान सम्मुच्चय $\mathbb {R} ^{2}$ के रूप में या मूल्यों के साथ दो रैखिक समीकरणों के समाधान सम्मुच्चय $\mathbb {R} ^{3}$ के रूप में होता है।

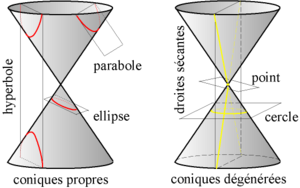
एक शंकु खंड समीकरण $x^{2}+y^{2}=z^{2}$ के साथ एक तल शंकु का प्रतिच्छेदन है। दूसरे शब्दों में, स्थल में, सभी शांकवों को तल के समीकरण और अभी दिए गए शंकु के समीकरण के हल समुच्चय के रूप में परिभाषित किया जाता है। यह औपचारिकता किसी को एक शंकु के केंद्रबिन्दु की स्थिति और गुणों को निर्धारित करने की अनुमति देती है।

समीकरणों के उपयोग से ज्यामितीय प्रश्नों को हल करने के लिए गणित के एक बड़े क्षेत्र पर आवाहन करने की अनुमति मिलती है। कार्तीय समन्वय प्रणाली ज्यामितीय समस्या को एक विश्लेषण समस्या में बदल देती है, एक बार जब आंकड़े समीकरणों में परिवर्तित हो जाते हैं तो उनको विश्लेषणात्मक ज्यामिति नाम दिया जाता है। डेसकार्टेस द्वारा उल्लिखित यह दृष्टिकोण, प्राचीन ग्रीक गणितज्ञों द्वारा कल्पना की गई ज्यामिति के प्रकार को समृद्ध और संशोधित करता है।

वर्तमान में, विश्लेषणात्मक ज्यामिति गणित की एक सक्रिय शाखा को निर्दिष्ट करती है। हालांकि यह अभी भी आंकड़ों को चित्रित करने के लिए समीकरणों का उपयोग करता है, यह कार्यात्मक विश्लेषण और रैखिक बीजगणित जैसी अन्य परिष्कृत तकनीकों का भी उपयोग करता है।

कार्तीय समीकरण

कार्तीय समन्वय प्रणाली एक समन्वय प्रणाली है जो प्रत्येक बिंदु (ज्यामिति) को विशिष्ट रूप से एक तल (ज्यामिति) में संख्या निर्देशांक की एक जोड़ी द्वारा निर्दिष्ट करती है, जो कि धनात्मक और ऋणात्मक संख्याएँ हैं, जो लंबाई की एक ही इकाई का उपयोग करके चिह्नित किए गए हैं।

तीन कार्तीय निर्देशांकों के उपयोग से त्रि-आयामी स्थल (गणित) में किसी भी बिंदु की स्थिति निर्दिष्ट करने के लिए एक ही सिद्धांत का उपयोग किया जा सकता है, जो तीन परस्पर लंबवत तल के लिए हस्ताक्षरित दूरी हैं (या, समतुल्य रूप से, इसके लंबवत प्रक्षेपण द्वारा तीन परस्पर लंबवत रेखाओं पर हस्ताक्षरित है)।

लाल रंग में चिह्नित मूल पर केंद्रित त्रिज्या 2 के एक चक्र के साथ कार्टेशियन समन्वय प्रणाली। एक वृत्त का समीकरण है (x − a)² + (y − b)² = r² जहाँ a और b केंद्र के निर्देशांक हैं (a, b) और R त्रिज्या है।

17 वीं शताब्दी में रेने डेसकार्टेस (लैटिनीकरण (साहित्य) नाम: कार्टेसियस) द्वारा कार्तीय निर्देशांक के आविष्कार ने यूक्लिडियन ज्यामिति और बीजगणित के बीच पहला व्यवस्थित लिंक प्रदान करके गणित में क्रांति ला दी। कार्तीय समन्वय प्रणाली का उपयोग करते हुए, ज्यामितीय आकृतियों (जैसे घटता) को 'कार्तीय समीकरण' द्वारा वर्णित किया जा सकता है: बीजगणितीय समीकरण जिसमें आकृति पर स्थित बिंदुओं के निर्देशांक सम्मिलित होते हैं। उदाहरण के लिए, एक समतल में त्रिज्या 2 का एक वृत्त, जो एक विशेष बिंदु पर केन्द्रित होता है जिसे मूल कहा जाता है, को उन सभी बिंदुओं के समुच्चय के रूप में वर्णित किया जा सकता है जिनके निर्देशांक x और y समीकरण को संतुष्ट करते हैं। x² + y² = 4.

प्राचलिक समीकरण

Main article: Parametric equation

एक वक्र के लिए एक प्राचलिक समीकरण वक्र के बिंदुओं के निर्देशांक को एक चर (गणित) के कार्यों के रूप में व्यक्त करता है, जिसे एक मापदण्ड कहा जाता है। उदाहरण के लिए,

${\begin{aligned}x&=\cos t\\y&=\sin t\end{aligned}}$

यूनिट सर्कल के लिए प्राचलिक समीकरण हैं, जहां टी मापदण्ड है। साथ में, इन समीकरणों को वक्र का 'प्राचलिक प्रतिनिधित्व' कहा जाता है।

प्राचलिक समीकरण की धारणा को सतह (टोपोलॉजी), मैनिफोल्ड्स और मैनिफोल्ड के उच्च आयाम के बीजगणितीय विविधता के लिए सामान्यीकृत किया गया है, जिसमें कई गुना या विविधता के आयाम के बराबर मापदंडों की संख्या और समीकरणों की संख्या के बराबर है। उस स्थान का आयाम जिसमें कई गुना या विविधता पर विचार किया जाता है (वक्र के लिए आयाम एक है और एक मापदण्ड का उपयोग किया जाता है, सतहों के आयाम दो और दो मापदण्ड आदि के लिए)।

संख्या सिद्धांत

डायोफैंटाइन समीकरण

Main article: Diophantine equation

एक डायोफैंटाइन समीकरण दो या दो से अधिक अज्ञात में एक बहुपद समीकरण है जिसके लिए प्रकार्य # बहुपद जड़ों के केवल पूर्णांक शून्य की मांग की जाती है (एक पूर्णांक समाधान एक समाधान है जैसे कि सभी अज्ञात पूर्णांक मान लेते हैं)। एक रेखीय डायोफैंटाइन समीकरण एक बहुपद शून्य या एक की डिग्री के दो योगों के बीच का समीकरण है। रेखीय डायोफैंटाइन समीकरण का एक उदाहरण है ax + by = c जहाँ a, b और c स्थिरांक हैं। एक 'घातीय डायोफैंटाइन समीकरण' वह है जिसके लिए समीकरण की शर्तों के प्रतिपादक अज्ञात हो सकते हैं।

'डायोफैंटाइन समस्याओं' में अज्ञात चरों की तुलना में कम समीकरण होते हैं और इसमें सभी समीकरणों के लिए सही ढंग से काम करने वाले पूर्णांकों को खोजना सम्मिलित होता है। अधिक तकनीकी भाषा में, वे एक बीजगणितीय वक्र, बीजगणितीय सतह, या अधिक सामान्य वस्तु को परिभाषित करते हैं, और उस पर जाली बिंदुओं के बारे में पूछते हैं।

डायोफैंटाइन शब्द ग्रीक गणित # तीसरी शताब्दी के हेलेनिस्टिक, सिकंदरिया के डायोफैंटस को संदर्भित करता है, जिन्होंने इस तरह के समीकरणों का अध्ययन किया और बीजगणित में गणितीय प्रतीक पेश करने वाले पहले गणितज्ञों में से एक थे। डायोफैंटाइन समस्याओं का गणितीय अध्ययन जिसे डायोफैंटस ने शुरू किया था, उसे अब 'डायोफैंटाइन विश्लेषण' कहा जाता है।

बीजगणितीय और पारलौकिक संख्याएं

Main articles: Algebraic number and Transcendental number

एक बीजगणितीय संख्या एक संख्या है जो परिमेय संख्या गुणांकों के साथ एक चर में एक गैर-शून्य बहुपद समीकरण का एक समाधान है (या समतुल्य - समाशोधन हर द्वारा - पूर्णांक गुणांक के साथ)। पाई जैसी संख्याएँ|πजो बीजगणितीय नहीं हैं उन्हें पारलौकिक संख्या कहा जाता है। लगभग सभी वास्तविक संख्याएँ और सम्मिश्र संख्याएँ पारलौकिक हैं।

बीजगणितीय ज्यामिति

Main article: Algebraic geometry

बीजगणितीय ज्यामिति गणित की एक शाखा है, जो शास्त्रीय रूप से बहुपद समीकरणों के समाधान का अध्ययन करती है। आधुनिक बीजगणितीय ज्यामिति भाषा और ज्यामिति की समस्याओं के साथ अमूर्त बीजगणित की अधिक अमूर्त तकनीकों, विशेष रूप से क्रमविनिमेय बीजगणित पर आधारित है।

बीजगणितीय ज्यामिति में अध्ययन की मूलभूत वस्तुएँ बीजगणितीय विविधता हैं, जो बहुपद समीकरणों के प्रणाली के समाधान सम्मुच्चय की ज्यामितीय अभिव्यक्तियाँ हैं। बीजगणितीय किस्मों के सबसे अधिक अध्ययन किए गए वर्गों के उदाहरण हैं: समतल बीजगणितीय वक्र, जिसमें रेखा (ज्यामिति), वृत्त, परवलय, दीर्घवृत्त, अतिपरवलय, अण्डाकार वक्र जैसे घन वक्र और बर्नौली के लेम्निस्केट, और कैसिनी अंडाकार जैसे क्वार्टिक वक्र सम्मिलित हैं। समतल का एक बिंदु एक बीजगणितीय वक्र से संबंधित होता है यदि इसके निर्देशांक दिए गए बहुपद समीकरण को संतुष्ट करते हैं। मूल प्रश्नों में वक्र के एकवचन बिंदु, विभक्ति बिंदु और अनंत पर बिंदु जैसे विशेष रुचि के बिंदुओं का अध्ययन सम्मिलित है। अधिक उन्नत प्रश्नों में वक्र की टोपोलॉजी और विभिन्न समीकरणों द्वारा दिए गए वक्रों के बीच संबंध सम्मिलित होते हैं।

विभेदक समीकरण

Main article: Differential equation

एक अजीब आकर्षण, जो एक निश्चित अंतर समीकरण को हल करते समय उत्पन्न होता है

अवकल समीकरण एक गणित का समीकरण है जो कुछ फलनों (गणित) को उसके अवकलजों से संबंधित करता है। अनुप्रयोगों में, कार्य सामान्यतः भौतिक मात्रा का प्रतिनिधित्व करते हैं, यौगिक परिवर्तन की अपनी दरों का प्रतिनिधित्व करते हैं, और समीकरण दोनों के बीच संबंध को परिभाषित करता है। क्योंकि इस तरह के संबंध अत्यंत सामान्य हैं, भौतिक विज्ञान, इंजीनियरिंग, अर्थशास्त्र और जीव विज्ञान सहित कई विषयों में अवकल समीकरण प्रमुख भूमिका निभाते हैं।

शुद्ध गणित में, अंतर समीकरणों का कई अलग-अलग दृष्टिकोणों से अध्ययन किया जाता है, जो ज्यादातर उनके समाधान से संबंधित होते हैं - समीकरण को संतुष्ट करने वाले कार्यों का सम्मुच्चय। स्पष्ट सूत्रों द्वारा केवल सबसे सरल अवकल समीकरणों को हल किया जा सकता है; हालाँकि, किसी दिए गए अवकल समीकरण के समाधान के कुछ गुण उनके सटीक रूप को खोजे बिना निर्धारित किए जा सकते हैं।

यदि समाधान के लिए स्व-निहित सूत्र उपलब्ध नहीं है, तो कंप्यूटर का उपयोग करके समाधान को संख्यात्मक रूप से अनुमानित किया जा सकता है। गतिशील प्रणालियों का सिद्धांत अंतर समीकरणों द्वारा वर्णित प्रणालियों के गुणात्मक विश्लेषण पर जोर देता है, जबकि सटीकता की एक निश्चित डिग्री के साथ समाधान निर्धारित करने के लिए कई संख्यात्मक तरीके विकसित किए गए हैं।

साधारण अंतर समीकरण

Main article: Ordinary differential equation

एक साधारण अंतर समीकरण या ODE एक समीकरण है जिसमें एक स्वतंत्र चर और उसके व्युत्पादित का एक कार्य होता है। साधारण शब्द का प्रयोग आंशिक अंतर समीकरण के विपरीत किया जाता है, जो एक स्वतंत्र चर से अधिक के संबंध में हो सकता है।

रेखीय अवकल समीकरण, जिनके समाधान हैं जिन्हें जोड़ा जा सकता है और गुणांकों द्वारा गुणा किया जा सकता है, अच्छी तरह से परिभाषित और समझे जाते हैं, और सटीक बंद-रूप समाधान प्राप्त होते हैं। इसके विपरीत, ओडीई जिनमें योगात्मक समाधानों की कमी होती है, अरैखिक होते हैं, और उन्हें हल करना कहीं अधिक जटिल होता है, क्योंकि बंद रूप में प्राथमिक कार्यों द्वारा शायद ही कभी उनका प्रतिनिधित्व किया जा सकता है: इसके बजाय, ओडीई के सटीक और विश्लेषणात्मक समाधान श्रृंखला या अभिन्न रूप में होते हैं। हाथ से या कंप्यूटर द्वारा लागू ग्राफिकल और संख्यात्मक साधारण अंतर समीकरण पद्धति, ओडीई के समाधान का अनुमान लगा सकते हैं और शायद उपयोगी जानकारी प्राप्त कर सकते हैं, जो प्रायः सटीक, विश्लेषणात्मक समाधान के अभाव में पर्याप्त होती है।

आंशिक अंतर समीकरण

Main article: Partial differential equation

एक आंशिक अंतर समीकरण (पीडीई) एक अंतर समीकरण है जिसमें अज्ञात बहुभिन्नरूपी कलन और उनके आंशिक व्युत्पादित सम्मिलित हैं। (यह सामान्य अंतर समीकरणों के विपरीत है, जो एक चर और उनके व्युत्पादित के कार्यों से निपटते हैं।) पीडीई का उपयोग कई चर के कार्यों से जुड़ी समस्याओं को तैयार करने के लिए किया जाता है, और या तो हाथ से हल किया जाता है, या एक प्रासंगिक कंप्यूटर प्रतिरूप बनाने के लिए उपयोग किया जाता है। .

पीडीई का उपयोग विभिन्न प्रकार की घटनाओं जैसे ध्वनि, गर्मी, इलेक्ट्रोस्टाटिक्स, बिजली का गतिविज्ञान, द्रव प्रवाह, लोच (भौतिकी), या क्वांटम यांत्रिकी का वर्णन करने के लिए किया जा सकता है। पीडीई के संदर्भ में समान रूप से अलग-अलग भौतिक घटनाओं को औपचारिक रूप से औपचारिक रूप दिया जा सकता है। जिस तरह साधारण अंतर समीकरण प्रायः एक-आयामी गतिशील प्रणालियों का प्रतिरूप करते हैं, आंशिक अंतर समीकरण प्रायः बहुआयामी प्रणालियों का प्रतिरूप करते हैं। पीडीई अपने सामान्यीकरण को स्टोकास्टिक आंशिक अंतर समीकरणों में पाते हैं।

समीकरणों के प्रकार

समीकरणों को संक्रिया के प्रकार (गणित) और सम्मिलित मात्राओं के अनुसार वर्गीकृत किया जा सकता है। महत्वपूर्ण प्रकारों में सम्मिलित हैं:

• एक बीजगणितीय समीकरण या बहुपद समीकरण एक समीकरण है जिसमें दोनों पक्ष बहुपद होते हैं (बहुपद समीकरणों की प्रणाली भी देखें)। इन्हें बहुपद की डिग्री द्वारा आगे वर्गीकृत किया गया है:
  • डिग्री एक के लिए पारलौकिक समारोह
  • डिग्री दो के लिए द्विघात समीकरण
  • डिग्री तीन के लिए घन समीकरण
  • डिग्री चार के लिए क्वार्टिक समीकरण
  • डिग्री पांच के लिए क्विंटिक समीकरण
  • छह डिग्री के लिए sextic समीकरण
  • डिग्री सात के लिए सेप्टिक समीकरण
  • डिग्री आठ के लिए ऑक्टिक समीकरण
• एक डायोफैंटाइन समीकरण एक समीकरण है जहां अज्ञात को पूर्णांक होना आवश्यक है
• एक ट्रान्सेंडैंटल समीकरण एक ऐसा समीकरण है जिसमें इसके अज्ञात का एक पारलौकिक समीकरण सम्मिलित है
• प्राचलिक समीकरण एक ऐसा समीकरण है जिसमें चरों के समाधान को कुछ अन्य चरों के कार्यों के रूप में व्यक्त किया जाता है, जिन्हें समीकरणों में प्रदर्शित होने वाले मापदण्ड कहा जाता है
• एक कार्यात्मक समीकरण एक समीकरण है जिसमें अज्ञात सामान्य मात्रा के बजाय कार्य (गणित) हैं
• व्युत्पादित, इंटीग्रल और परिमित अंतर वाले समीकरण:
  • एक अंतर समीकरण एक कार्यात्मक समीकरण है जिसमें अज्ञात कार्यों के व्युत्पादित सम्मिलित होते हैं, जहां प्रकार्य और उसके व्युत्पादित का मूल्यांकन एक ही बिंदु पर किया जाता है, जैसे कि $f'(x)=x^{2}$. अवकल समीकरणों को एकल चर वाले फलनों के लिए सामान्य अवकल समीकरणों और अनेक चरों वाले फलनों के लिए आंशिक अवकल समीकरणों में उप-विभाजित किया जाता है।
  • एक अभिन्न समीकरण एक कार्यात्मक समीकरण है जिसमें अज्ञात कार्यों के प्रतिपक्षी सम्मिलित हैं। एक चर के कार्यों के लिए, ऐसा समीकरण एक अंतर समीकरण से भिन्न होता है, मुख्य रूप से इसके व्युत्पन्न द्वारा प्रकार्य को प्रतिस्थापित करने वाले चर के परिवर्तन के माध्यम से, हालांकि यह मामला नहीं है जब अभिन्न एक खुली सतह पर लिया जाता है
  • एक पूर्णांक-अंतर समीकरण एक कार्यात्मक समीकरण है जिसमें अज्ञात कार्यों के व्युत्पादित और antiderivative दोनों सम्मिलित हैं। एक चर के कार्यों के लिए, ऐसा समीकरण चर के समान परिवर्तन के माध्यम से अभिन्न और अंतर समीकरणों से भिन्न होता है।
  • देरी अंतर समीकरण का एक कार्यात्मक अंतर समीकरण एक प्रकार्य समीकरण है जिसमें अज्ञात कार्यों के व्युत्पादित सम्मिलित हैं, जिनका मूल्यांकन कई बिंदुओं पर किया जाता है, जैसे $f'(x)=f(x-2)$
  • एक अंतर समीकरण एक समीकरण है जहां अज्ञात एक फलन f है जो समीकरण में f(x), f(x−1), ..., f(x−k) के माध्यम से होता है, कुछ पूर्ण पूर्णांक k के लिए कहा जाता है समीकरण का क्रम। यदि x को एक पूर्णांक के रूप में प्रतिबंधित किया जाता है, तो एक अंतर समीकरण पुनरावृत्ति संबंध के समान होता है
  • एक स्टोचैस्टिक अंतर समीकरण एक डिफरेंशियल इक्वेशन है जिसमें एक या अधिक शब्द एक स्टोकेस्टिक प्रक्रिया है

यह भी देखें

• सूत्र
• बीजगणित का इतिहास
• अनिश्चित समीकरण
• समीकरणों की सूची
• लोगों के नाम पर वैज्ञानिक समीकरणों की सूची
• अवधि (तर्क)
• समीकरणों का सिद्धांत
• रद्द करना

बाहरी कड़ियाँ

• Winplot: General Purpose plotter that can draw and animate 2D and 3D mathematical equations.
• Equation plotter: A web page for producing and downloading pdf or postscript plots of the solution sets to equations and inequations in two variables (x and y).

श्रेणी: प्रारंभिक बीजगणित