क्लेनियन समूह
| बीजगणितीय संरचना → 'समूह सिद्धांत' समूह सिद्धांत |
|---|
 |
गणित में, क्लेनियन समूह अतिशयोक्तिपूर्ण 3-स्थान वाले अभिविन्यास-संरक्षण नियम के अनुसार आइसोमेट्री के समूह (गणित) का अलग उपसमूह H3 है, इसके पश्चात, PSL(2,C) के साथ या PSL(2, C) के साथ इसे पहचाना जा सकता है, इसके [[केंद्र (समूह सिद्धांत)]] द्वारा निर्धारक 1 के 2 बटा 2 जटिल संख्या आव्यूह (गणित) का भागफल समूह प्राप्त होता है, जिसमें पहचाने गए इस आव्यूह और इसके उत्पाद उपस्थिति होते हैं, इस प्रकार −1. PSL(2, C) रीमैन क्षेत्र के अभिविन्यास-संरक्षण अनुरूप परिवर्तन के रूप में और संवृत इकाई गेंद के अभिविन्यास-संरक्षण अनुरूप परिवर्तनों के रूप में प्राकृतिक प्रतिनिधित्व B3 में R3 को प्रदर्शित करता है, इस प्रकार मोबियस परिवर्तन के समूह या मोबियस परिवर्तन गैर-अभिविन्यास-संरक्षण आइसोमेट्री समूह के रूप H3, PGL(2, C). में भी संबंधित है, इसके आधार पर यह या तो क्लेनियन समूह को इनमें से किसी स्थान पर अलग उपसमूह समूह प्रक्रिया के रूप में माना जा सकता है।
इतिहास
सामान्य क्लेनियन समूहों के सिद्धांत की स्थापना किसके द्वारा की गई थी? फेलिक्स क्लेइन (1883) और हेनरी पोइनकेयर (1883), जिन्होंने उनका नाम फ़ेलिक्स क्लेन के नाम पर रखा था। इस प्रकार शॉट्की समूहों की विशेष स्थितियों का अध्ययन कुछ वर्ष पहले 1877 में, शॉट्की द्वारा किया गया था।
परिभाषाएँ
क्लेनियन समूह की आधुनिक परिभाषा ऐसे समूह के रूप में है जो 3-बॉल पर कार्य करता है, इस प्रकार हाइपरबोलिक आइसोमेट्रीज़ के अलग समूह के रूप में प्राप्त होते हैं। इसका कारण यह हैं कि हाइपरबोलिक 3-स्पेस की प्राकृतिक सीमाएँ होती है, इस प्रकार बॉल प्रारूप में, इसे 2-गोलो की सहायता से पहचाना जा सकता है। हम इसे अनंत पर गोला कहते हैं और इसे से निरूपित करते हैं, इस प्रकार हाइपरबोलिक आइसोमेट्री अनंत पर गोले के अनुरूप होमियोमोर्फिज्म तक फैली हुई है, और इसके विपरीत, अनंत पर गोले पर प्रत्येक अनुरूप होमियोमोर्फिज्म पोंकारे विस्तार द्वारा गेंद पर हाइपरबोलिक आइसोमेट्री तक विशिष्ट रूप से विस्तारित होता है। यह जटिल विश्लेषण से मानक परिणाम है जो अनुरूप होमियोमोर्फिज्म पर आधारित है। इस प्रकार रीमैन क्षेत्र वास्तव में मोबियस परिवर्तन है, इसके कारण मोबियस परिवर्तन, जिसे आगे प्रक्षेप्य रैखिक समूह पीजीएल (2, सी) के तत्वों के रूप में पहचाना जा सकता है। इस प्रकार, क्लेनियन समूह को पीजीएल (2, सी) के उपसमूह Γ के रूप में भी परिभाषित किया जा सकता है, मौलिक रूप से, क्लेनियन समूह को रीमैन क्षेत्र के संवृत उपसमूह पर उचित रूप से असंतत रूप से कार्य करने की आवश्यकता थी, अपितु आधुनिक उपयोग किसी भी अलग उपसमूह की अनुमति देता है।
जब Γ मौलिक समूह के लिए का मान समरूपी होता है, इस प्रकार अतिशयोक्तिपूर्ण 3-मैनिफोल्ड का, फिर भागफल स्थान (टोपोलॉजी) H3/Γ मैनिफोल्ड का क्लेनियन प्रारूप बन जाता है। कई लेखक क्लेनियन प्रारूप और क्लेनियन समूह शब्दों का परस्पर उपयोग करते हैं, जिससे को दूसरे के लिए खड़ा किया जाता है।
विसंगति का तात्पर्य है कि हाइपरबोलिक 3-स्पेस के आंतरिक भाग में बिंदुओं में परिमित स्टेबलाइज़र (समूह सिद्धांत), और समूह Γ के अंतर्गत असतत कक्षा (समूह सिद्धांत) है। इसी प्रकार इसके दूसरी ओर, बिंदु p की कक्षा Γp सामान्यतः विवृत गेंद की सीमा पर संचय बिंदु होगा।
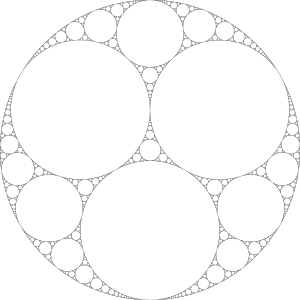
Γp के संचय बिंदुओं का समुच्चय का सीमा समुच्चय कहा जाता है, और सामान्यतः इसे द्वारा दर्शाया जाता है, यहाँ पर पूरक असंततता का क्षेत्र या साधारण समुच्चय या नियमित समुच्चय कहा जाता है। इसके अनुसार अहलफ़ोर्स की परिमितता प्रमेय का तात्पर्य यह है कि यदि समूह परिमित रूप से उत्पन्न होता है, जिसकी परिमित प्रकार की रीमैन सतह इसकी विभिन्न कक्षाओं द्वारा प्रदर्शित होती हैं।
यूनिट बॉल B3 अपनी अनुरूप संरचना के साथ पोंकारे अर्ध-तल प्रारूप है | इसके कारण हाइपरबोलिक 3-स्पेस का पोंकारे का प्रारूप हैं। इस प्रकार जब हम इसके बारे में मीट्रिक के साथ, मीट्रिक के साथ सोचते हैं, तो हमें यह समीकरण प्राप्त होता हैं।
यह 3-आयामी हाइपरबोलिक स्पेस H3 का प्रारूप है, इस प्रकार B3H3 के अनुरूप स्व-मानचित्रों का समुच्चय के सममिति अर्ताथ दूरी-संरक्षण मानचित्र के समुच्चय बन जाता है, इस पहचान के अनुसार ऐसे मानचित्र अनुरूप स्व-मानचित्रों तक सीमित होते हैं, जो मोबियस का परिवर्तन हैं। इस प्रकार समरूपताएँ इस समीकरण द्वारा प्रदर्शित होती हैं-
इन समूहों के उपसमूह, जिनमें अभिविन्यास-संरक्षण परिवर्तन सम्मिलित हैं, इस प्रकार प्रक्षेप्य आव्यूह समूह के सभी समरूपी हैं: यहाँ पर PSL(2,C) जटिल प्रक्षेप्य रेखा P1(C) के साथ इकाई क्षेत्र की सामान्य पहचान के माध्यम से की जाती हैं।
विविधताएं
क्लेनियन समूह की परिभाषा में कुछ भिन्नताएँ हैं: कभी-कभी क्लेनियन समूहों को PSL(2, C).2 अर्थात, जटिल संयुग्मन द्वारा विस्तारित PSL(2, C) के उपसमूह होने की अनुमति है, दूसरे शब्दों में, तत्वों को उलटने वाले अभिविन्यास के लिए, और कभी-कभी उन्हें परिमित रूप से माना जाता है, इस प्रकार से उत्पन्न होने वाले समूहों, और कभी-कभी उन्हें रीमैन क्षेत्र के गैर-रिक्त संवृत उपसमुच्चय पर उचित रूप से असंतत रूप से कार्य करने की आवश्यकता होती है।
प्रकार
- एक क्लेनियन समूह को परिमित प्रकार का कहा जाता है, यदि इसके असंतत क्षेत्र में समूह क्रिया के अनुसार घटकों की कक्षाओं की सीमित संख्या होती है, और इसके स्टेबलाइज़र द्वारा प्रत्येक घटक का भागफल कॉम्पैक्ट रीमैन सतह होता है, जिसमें कई बिंदु हटा दिए जाते हैं, और आवरण अनेक बिंदुओं पर व्याप्त है।
- एक क्लेनियन समूह को परिमित रूप से उत्पन्न कहा जाता है, यदि इसमें जनरेटर की संख्या सीमित है। इस प्रकार अहलफोर्स परिमितता प्रमेय कहता है कि ऐसा समूह परिमित प्रकार का होता है।
- एक क्लेनियन समूह Γ में परिमित सहआयतन होता है, यदि H3/Γ का आयतन सीमित है। परिमित कोवॉल्यूम का कोई भी क्लेनियन समूह परिमित रूप से उत्पन्न होता है।
- एक क्लेनियन समूह को ज्यामितीय रूप से परिमित कहा जाता है, यदि इसमें मौलिक बहुफलक (अतिपरवलयिक 3-स्थान में) और परिमित रूप से कई भुजाएँ रहती हैं। इस प्रकार अहलफोर्स ने दिखाया कि यदि निर्धारित सीमा संपूर्ण रीमैन क्षेत्र नहीं है तो इसका माप 0 है।
- एक क्लेनियन समूह Γ को अंकगणित कहा जाता है, यदि यह चतुर्धातुक बीजगणित ए के क्रम के समूह मानदंड 1 तत्वों के साथ तुलनीय है, जो संख्या क्षेत्र के पर सभी वास्तविक स्थानों पर बिल्कुल जटिल स्थान के साथ जुड़ा हुआ है। इसके अंकगणितीय क्लेनियन समूहों में परिमित सहआयतन होती है।
- एक क्लेनियन समूह Γ को कोकॉम्पैक्ट कहा जाता है, यदि H3/Γ सघन है, या समकक्ष SL(2, C)/Γ सघन है। कोकॉम्पैक्ट क्लेनियन समूहों में सीमित मात्रा होती है।
- एक क्लेनियन समूह को स्थलीय रूप से वश में कहा जाता है यदि यह परिमित रूप से उत्पन्न होता है और इसका हाइपरबोलिक मैनिफोल्ड सीमाओं के साथ कॉम्पैक्ट मैनिफोल्ड के इंटीरियर के लिए होमियोमॉर्फिक है।
- एक क्लेनियन समूह को ज्यामितीय रूप से अधिकृत कर लिया जाता है, यदि इसके सिरे या तो ज्यामितीय रूप से परिमित हों या केवल (थर्स्टन 1980) के विकृत रूप में हो।
- एक क्लेनियन समूह को प्रकार 1 का कहा जाता है यदि सीमा निर्धारित संपूर्ण रीमैन क्षेत्र है, और अन्यथा प्रकार 2 का होता है।
उदाहरण
- बेर्स क्लेनियन समूहों के मॉड्यूलि स्पेस को काटते हैं।
बियांची समूह
बियांची समूह मुख्य रूप से PSL(2, Od) रूप का क्लेनियन समूह है, जहाँ मुख्य रूप से काल्पनिक द्विघात क्षेत्र के पूर्णांकों का वलय है, जो d के लिए धनात्मक वर्ग-मुक्त पूर्णांक के समान हैं।
प्राथमिक और कम करने योग्य क्लेनियन समूह
एक क्लेनियन समूह को प्रारंभिक कहा जाता है यदि इसका सीमा समुच्चय परिमित है, जिस स्थिति में सीमा समुच्चय में 0, 1 या 2 अंक हैं।
प्राथमिक क्लेनियन समूहों के उदाहरणों में परिमित क्लेनियन समूह इसकी रिक्त सीमा समुच्चय के साथ और अनंत चक्रीय क्लेनियन समूह सम्मिलित हैं।
यदि सभी तत्वों का रीमैन क्षेत्र पर सामान्य निश्चित बिंदु हो तो क्लेनियन समूह को रिड्यूसिबल कहा जाता है। रिड्यूसिबल क्लेनियन समूह प्राथमिक हैं, अपितु कुछ प्राथमिक परिमित क्लेनियन समूह रिड्यूसबल नहीं हैं।
फ़ुच्सियन समूह
कोई भी फ़ुचियन समूह (PSL(2, R) का अलग उपसमूह क्लेनियन समूह है, और इसके विपरीत कोई भी क्लेनियन समूह जो वास्तविक रेखा को संरक्षित करता है, जहाँ रीमैन क्षेत्र पर अपनी प्रतिक्रिया में फ़ुचियन समूह है। अधिक सामान्यतः रीमैन क्षेत्र में वृत्त या सीधी रेखा को संरक्षित करने वाला प्रत्येक क्लेनियन समूह फ़ुचियन समूह से संयुग्मित होता है।
कोएबे समूह
- क्लेनियन समूह G का कारक निम्नलिखित गुणों के अधीन उपसमूह H से अधिकतम है:
- H में सरल रूप से जुड़ा हुआ अपरिवर्तनीय घटक D है
- अनुरूप आक्षेप द्वारा H के तत्व h का संयुग्म परवलयिक या अण्डाकार होता है यदि और केवल यदि h हो।
- G का कोई भी परवलयिक तत्व D के सीमा बिंदु को तय करने वाला H में है।
- एक क्लेनियन समूह को कोएबे समूह कहा जाता है यदि इसके सभी कारक प्राथमिक या फ़ुचियन हैं।
अर्ध-फ़ुचियन समूह
एक क्लेनियन समूह जो जॉर्डन वक्र को संरक्षित करता है, उसे अर्ध-फुचियन समूह कहा जाता है। जब जॉर्डन वक्र वृत्त या सीधी रेखा होता है तो ये अनुरूप परिवर्तनों के अनुसार फुच्सियन समूहों से संयुग्मित होते हैं। इसके अंतिम रूप से उत्पन्न होने वाले अर्ध-फ़ुचियन समूह अर्ध-अनुरूप परिवर्तनों के अनुसार फ़ुचियन समूहों से संयुग्मित होते हैं। सीमा निर्धारित अपरिवर्तनीय जॉर्डन वक्र में निहित है, और यदि यह जॉर्डन वक्र के समान है, तो समूह को पहली तरह का कहा जाता है, और अन्यथा इसे दूसरी तरह का कहा जाता है।
शोट्की समूह
इस प्रकार Ci असंयुक्त बंद डिस्क के सीमित संग्रह की सीमा वृत्त बनते हैं। जिसके लिए प्रत्येक वृत्त में वृत्त व्युत्क्रम द्वारा उत्पन्न समूह की सीमा कैंटर समुच्चय और भागफल H3/G है, जिसका दर्पण कक्षीय गुना है जिसके नीचे गेंद है। यह हैंडलबॉडी द्वारा डबल कवर (टोपोलॉजी) है, इस प्रकार उपसमूह 2 उपसमूह का संगत सूचकांक क्लेनियन समूह है, जिसे शोट्की समूह कहा जाता है।
क्रिस्टलोग्राफिक समूह
मान लीजिए कि T हाइपरबोलिक 3-स्पेस का आवृत्ति वर्गाकार होती है। इस प्रकार टेस्सेलेशन की समरूपता का समूह मुख्य रूप से क्लेनियन समूह को दर्शाता है।
अतिशयोक्तिपूर्ण 3-मैनिफोल्ड्स के मौलिक समूह
किसी भी उन्मुख हाइपरबोलिक 3-मैनिफोल्ड का मूल समूह क्लेनियन समूह है। इसके कई उदाहरण हैं, जैसे कि आकृति 8 गाँठ का पूरक या सीफर्ट-वेबर स्पेस। इसके विपरीत यदि किसी क्लेनियन समूह में किसी मैनिफोल्ड के तत्व नहीं है, तो यह अतिशयोक्तिपूर्ण 3-मैनिफोल्ड का मूल समूह है।
पतित क्लेनियन समूह
एक क्लेनियन समूह को पतित कहा जाता है यदि यह प्राथमिक नहीं है और इसका सीमा समुच्चय बस जुड़ा हुआ है। ऐसे समूहों का निर्माण अर्ध-फ़ुचियन समूहों की उपयुक्त सीमा लेकर किया जा सकता है, जिससे कि नियमित बिंदुओं के दो घटकों में से रिक्त समुच्चय तक सिकुड़ जाए, जिसके कारण इन समूहों को एकल पतित कहा जाता है। यदि नियमित समुच्चय के दोनों घटक रिक्त समुच्चय की ओर सिकुड़ते हैं, तो सीमा समुच्चय स्थान-भरण वक्र बन जाता है और समूह को दोगुना पतित कहा जाता है।
पतित क्लेनियन समूहों का अस्तित्व सबसे पहले अप्रत्यक्ष रूप से बेर्स (1970) द्वारा दिखाया गया था, और इसका पहला स्पष्ट उदाहरण जोर्गेंसन द्वारा पाया गया था। कैनन & थर्स्टन (2007) ने स्यूडो-एनोसोव मानचित्र से संयोजित होने वाले दोगुने पतित समूहों और स्थान-भरने वाले वक्रों के उदाहरण दिए थे।
यह भी देखें
- अहलफोर्स अनुमान को मापते हैं।
- क्लेनियन समूहों के लिए घनत्व प्रमेय का उपयोग किया जाता हैं।
- लेमिनेशन प्रमेय को समाप्त किया जाता हैं।
- तमता प्रमेय (मार्डन का अनुमान)
संदर्भ
- Bers, Lipman (1970), "On boundaries of Teichmüller spaces and on Kleinian groups. I", Annals of Mathematics, Second Series, 91 (3): 570–600, doi:10.2307/1970638, ISSN 0003-486X, JSTOR 1970638, MR 0297992
- Bers, Lipman; Kra, Irwin, eds. (1974), A crash course on Kleinian groups (PDF), Lecture Notes in Mathematics, vol. 400, Berlin, New York: Springer-Verlag, doi:10.1007/BFb0065671, hdl:10077/4140, ISBN 978-3-540-06840-2, MR 0346152
- Cannon, James W.; Thurston, William P. (2007) [1982], "Group invariant Peano curves", Geometry & Topology, 11 (3): 1315–1355, doi:10.2140/gt.2007.11.1315, ISSN 1465-3060, MR 2326947
- Fricke, Robert; Klein, Felix (1897), Vorlesungen über die Theorie der automorphen Functionen. Erster Band; Die gruppentheoretischen Grundlagen (in Deutsch), Leipzig: B. G. Teubner, ISBN 978-1-4297-0551-6, JFM 28.0334.01
- Fricke, Robert; Klein, Felix (1912), Vorlesungen über die Theorie der automorphen Functionen. Zweiter Band: Die funktionentheoretischen Ausführungen und die Anwendungen. 1. Lieferung: Engere Theorie der automorphen Funktionen (in Deutsch), Leipzig: B. G. Teubner., ISBN 978-1-4297-0552-3, JFM 32.0430.01
- Harvey, William James (1978), "Kleinian groups (a survey).", Séminaire Bourbaki, 29e année (1976/77), Exp. No. 491, Lecture Notes in Math., vol. 677, Springer, Berlin, pp. 30–45, doi:10.1007/BFb0070752, ISBN 978-3-540-08937-7, MR 0521758
- Kapovich, Michael (2009) [2001], Hyperbolic manifolds and discrete groups, Modern Birkhäuser Classics, Boston, MA: Birkhäuser Boston, doi:10.1007/978-0-8176-4913-5, ISBN 978-0-8176-4912-8, MR 1792613
- Klein, Felix (1883), "Neue Beiträge zur Riemann'schen Functionentheorie", Mathematische Annalen, 21 (2): 141–218, doi:10.1007/BF01442920, ISSN 0025-5831, JFM 15.0351.01, S2CID 120465625
- Kra, Irwin (1972), Automorphic forms and Kleinian groups, Mathematics Lecture Note Series, W. A. Benjamin, Inc., Reading, Mass., ISBN 9780805323429, MR 0357775
- Krushkal, S.L. (2001) [1994], "Kleinian group", Encyclopedia of Mathematics, EMS Press
- Maclachlan, Colin; Reid, Alan W. (2003), The arithmetic of hyperbolic 3-manifolds, Graduate Texts in Mathematics, vol. 219, Berlin, New York: Springer-Verlag, CiteSeerX 10.1.1.169.1318, doi:10.1007/978-1-4757-6720-9, ISBN 978-0-387-98386-8, MR 1937957
- Maskit, Bernard (1988), Kleinian groups, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 287, Berlin, New York: Springer-Verlag, ISBN 978-3-540-17746-3, MR 0959135
- Matsuzaki, Katsuhiko; Taniguchi, Masahiko (1998), Hyperbolic manifolds and Kleinian groups, Oxford Mathematical Monographs, The Clarendon Press Oxford University Press, ISBN 978-0-19-850062-9, MR 1638795
- Mumford, David; Series, Caroline; Wright, David (2002), Indra's pearls, Cambridge University Press, doi:10.1017/CBO9781107050051.024, ISBN 978-0-521-35253-6, MR 1913879
- Poincaré, Henri (1883), "Mémoire sur Les groupes kleinéens", Acta Mathematica, 3: 49–92, doi:10.1007/BF02422441, ISSN 0001-5962, JFM 15.0348.02
- Series, Caroline (2005), "A crash course on Kleinian groups", Rendiconti dell'Istituto di Matematica dell'Università di Trieste, 37 (1): 1–38, ISSN 0049-4704, MR 2227047, archived from the original on 2011-07-22
- Thurston, William (1980), The geometry and topology of three-manifolds, Princeton lecture notes
- Thurston, William P. (1982), "Three-dimensional manifolds, Kleinian groups and hyperbolic geometry", Bulletin of the American Mathematical Society, New Series, 6 (3): 357–381, doi:10.1090/S0273-0979-1982-15003-0, ISSN 0002-9904, MR 0648524
बाहरी संबंध
- A picture of the limit set of a quasi-Fuchsian group from (Fricke & Klein 1897, p. 418).
- A picture of the limit set of a Kleinian group from (Fricke & Klein 1897, p. 440). This was one of the first pictures of a limit set. A computer drawing of the same limit set
- Animations of Kleinian group limit sets
- Images related to Kleinian groups by McMullen
- Weisstein, Eric W. "Kleinian Group". MathWorld.
