वास्तविक चर का कार्य

गणितीय विश्लेषण में, और ज्यामिति, अनुप्रयुक्त गणित, अभियांत्रिकी और प्राकृतिक विज्ञान में अनुप्रयोगों में, एक वास्तविक चर का एक फ़ंक्शन एक फ़ंक्शन (गणित) होता है जिसका फ़ंक्शन का डोमेन वास्तविक संख्याएं होता है $\mathbb {R}$, या का एक उपसमूह $\mathbb {R}$ जिसमें सकारात्मक लंबाई का एक अंतराल (गणित) शामिल है। जिन अधिकांश वास्तविक कार्यों पर विचार और अध्ययन किया जाता है वे कुछ अंतराल में अवकलनीय कार्य होते हैं। सबसे व्यापक रूप से माने जाने वाले ऐसे फ़ंक्शन वास्तविक फ़ंक्शन होते हैं, जो एक वास्तविक चर के वास्तविक-मूल्य वाले फ़ंक्शन होते हैं, अर्थात, एक वास्तविक चर के फ़ंक्शन जिसका कोडोमेन वास्तविक संख्याओं का सेट होता है।

फिर भी, वास्तविक चर के फ़ंक्शन का कोडोमेन कोई भी सेट हो सकता है। हालाँकि, अक्सर यह माना जाता है कि इसकी एक संरचना है $\mathbb {R}$-वास्तविकता पर वेक्टर स्थान। अर्थात्, कोडोमेन एक यूक्लिडियन स्थान , एक समन्वय वेक्टर, किसी दिए गए आकार की वास्तविक संख्याओं के मैट्रिक्स (गणित) का सेट, या एक हो सकता है $\mathbb {R}$-किसी क्षेत्र पर बीजगणित, जैसे सम्मिश्र संख्याएँ या चतुर्भुज। ढांचा $\mathbb {R}$-कोडोमेन का वेक्टर स्पेस एक संरचना को प्रेरित करता है $\mathbb {R}$-फ़ंक्शंस पर वेक्टर स्पेस। यदि कोडोमेन की संरचना है $\mathbb {R}$-बीजगणित, फ़ंक्शंस के लिए भी यही सच है।

एक वास्तविक चर के फ़ंक्शन की छवि (गणित) कोडोमेन में एक वक्र (गणित) है। इस संदर्भ में, वक्र को परिभाषित करने वाला फ़ंक्शन वक्र का पैरामीट्रिक समीकरण कहलाता है।

जब किसी वास्तविक चर के फ़ंक्शन का कोडोमेन एक परिमित-आयामी वेक्टर स्थान होता है, तो फ़ंक्शन को वास्तविक कार्यों के अनुक्रम के रूप में देखा जा सकता है। इसका उपयोग अक्सर अनुप्रयोगों में किया जाता है।

वास्तविक कार्य

एक वास्तविक फ़ंक्शन का ग्राफ़

एक वास्तविक फलन एक उपसमुच्चय से प्राप्त फलन (गणित) है $\mathbb {R}$ को $\mathbb {R} ,$ कहाँ $\mathbb {R}$ हमेशा की तरह वास्तविक संख्याओं के समुच्चय को दर्शाता है। अर्थात्, किसी वास्तविक फलन के फलन का डोमेन एक उपसमुच्चय होता है $\mathbb {R}$, और इसका कोडोमेन है $\mathbb {R} .$ आम तौर पर यह माना जाता है कि डोमेन में सकारात्मक लंबाई का अंतराल (गणित) होता है।

बुनियादी उदाहरण

आमतौर पर उपयोग किए जाने वाले कई वास्तविक फ़ंक्शंस के लिए, डोमेन वास्तविक संख्याओं का संपूर्ण सेट होता है, और फ़ंक्शन डोमेन के प्रत्येक बिंदु पर निरंतर फ़ंक्शन और भिन्न फ़ंक्शन होता है। एक का कहना है कि ये कार्य हर जगह परिभाषित, निरंतर और भिन्न होते हैं। यह मामला है:

• स्थिर फलन और रैखिक फलन (कैलकुलस) सहित सभी बहुपद फलन
• ज्या और कोज्या कार्य
• घातांक प्रकार्य

कुछ फ़ंक्शन हर जगह परिभाषित होते हैं, लेकिन कुछ बिंदुओं पर निरंतर नहीं होते हैं। उदाहरण के लिए

• हेविसाइड निरंतर कार्य को हर जगह परिभाषित किया गया है, लेकिन शून्य पर निरंतर नहीं।

कुछ कार्य हर जगह परिभाषित और निरंतर होते हैं, लेकिन हर जगह भिन्न नहीं होते। उदाहरण के लिए

• निरपेक्ष मान हर जगह परिभाषित और निरंतर है, और शून्य को छोड़कर, हर जगह अलग-अलग है।
• घनमूल हर जगह परिभाषित और निरंतर है, और शून्य को छोड़कर, हर जगह अलग-अलग है।

कई सामान्य कार्यों को हर जगह परिभाषित नहीं किया जाता है, लेकिन जहां भी उन्हें परिभाषित किया जाता है, वे निरंतर और भिन्न होते हैं। उदाहरण के लिए:

• एक परिमेय फलन दो बहुपद फलनों का भागफल होता है, और हर के फलन के शून्य पर परिभाषित नहीं होता है।
• स्पर्शरेखा फलन को परिभाषित नहीं किया गया है ${\frac {\pi }{2}}+k\pi ,$ कहाँ k कोई पूर्णांक है.
• लघुगणक फ़ंक्शन केवल चर के सकारात्मक मानों के लिए परिभाषित किया गया है।

कुछ फ़ंक्शन अपने पूरे डोमेन में निरंतर होते हैं, और कुछ बिंदुओं पर भिन्न नहीं होते हैं। यह मामला है:

• वर्गमूल को केवल चर के गैर-नकारात्मक मानों के लिए परिभाषित किया गया है, और 0 पर अवकलनीय नहीं है (यह चर के सभी सकारात्मक मानों के लिए अवकलनीय है)।

सामान्य परिभाषा

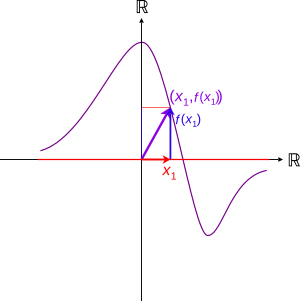
एक वास्तविक चर का वास्तविक-मूल्यवान फ़ंक्शन एक फ़ंक्शन (गणित) है जो इनपुट के रूप में एक वास्तविक संख्या लेता है, जिसे आमतौर पर चर (गणित) x द्वारा दर्शाया जाता है, एक और वास्तविक संख्या उत्पन्न करने के लिए, का मान फ़ंक्शन, जिसे आमतौर पर f(x) कहा जाता है। सरलता के लिए, इस लेख में एक वास्तविक चर के वास्तविक-मूल्यवान फ़ंक्शन को केवल एक फ़ंक्शन कहा जाएगा। किसी भी अस्पष्टता से बचने के लिए, होने वाले अन्य प्रकार के कार्यों को स्पष्ट रूप से निर्दिष्ट किया जाएगा।

कुछ फ़ंक्शंस को चर के सभी वास्तविक मानों के लिए परिभाषित किया गया है (कोई कहता है कि वे हर जगह परिभाषित हैं), लेकिन कुछ अन्य फ़ंक्शंस केवल तभी परिभाषित किए जाते हैं यदि चर का मान ℝ के उपसमुच्चय X में लिया जाता है, जिसका डोमेन फ़ंक्शन का एक फ़ंक्शन, जिसमें हमेशा सकारात्मक लंबाई का अंतराल (गणित) शामिल होता है। दूसरे शब्दों में, वास्तविक चर का वास्तविक-मूल्यवान फ़ंक्शन एक फ़ंक्शन है

$f:X\to \mathbb {R}$

ऐसा कि इसका डोमेन X ℝ का एक उपसमुच्चय है जिसमें सकारात्मक लंबाई का अंतराल होता है।

एक वेरिएबल में किसी फ़ंक्शन का एक सरल उदाहरण हो सकता है:

$f:X\to \mathbb {R}$

$X=\{x\in \mathbb {R} \,:\,x\geq 0\}$

$f(x)={\sqrt {x}}$

जो x का वर्गमूल है.

छवि

Main article: Image (mathematics)

किसी फ़ंक्शन की छवि (गणित)। $f(x)$ के सभी मानों का समुच्चय है f जब वेरिएबल x पूरे डोमेन में चलता है f. किसी कनेक्टेड डोमेन के साथ निरंतर (परिभाषा के लिए नीचे देखें) वास्तविक-मूल्य वाले फ़ंक्शन के लिए, छवि या तो एक अंतराल (गणित) या एकल मान है। बाद वाले मामले में, फ़ंक्शन एक स्थिर फ़ंक्शन है।

किसी दी गई वास्तविक संख्या y की पूर्वछवि समीकरण के समाधानों का समुच्चय है y = f(x).

डोमेन

कई वास्तविक चर वाले फ़ंक्शन का डोमेन ℝ का एक उपसमुच्चय है जिसे कभी-कभी स्पष्ट रूप से परिभाषित किया जाता है। वास्तव में, यदि कोई किसी फ़ंक्शन f के डोमेन X को उपसमुच्चय Y ⊂_|Y. व्यवहार में, एफ और एफ की पहचान करना अक्सर हानिकारक नहीं होता है_|Y, और सबस्क्रिप्ट को छोड़ना _|Y.

इसके विपरीत, कभी-कभी किसी दिए गए फ़ंक्शन के डोमेन को स्वाभाविक रूप से बढ़ाना संभव होता है, उदाहरण के लिए निरंतर फ़ंक्शन या विश्लेषणात्मक निरंतरता द्वारा। इसका मतलब यह है कि यह वास्तविक चर के फ़ंक्शन के डोमेन को स्पष्ट रूप से परिभाषित करने के योग्य नहीं है।

बीजगणितीय संरचना

अंकगणितीय परिचालनों को निम्नलिखित तरीके से कार्यों पर लागू किया जा सकता है:

• प्रत्येक वास्तविक संख्या r के लिए, स्थिर फलन $(x)\mapsto r$, हर जगह परिभाषित है।
• प्रत्येक वास्तविक संख्या r और प्रत्येक फ़ंक्शन f के लिए, फ़ंक्शन $rf:(x)\mapsto rf(x)$ इसका डोमेन f के समान है (या यदि r = 0 है तो इसे हर जगह परिभाषित किया गया है)।
• यदि f और g संबंधित डोमेन X और Y के दो फ़ंक्शन हैं जैसे कि X∩Y में ℝ का एक खुला उपसमुच्चय शामिल है $f+g:(x)\mapsto f(x)+g(x)$ और $f\,g:(x)\mapsto f(x)\,g(x)$ ऐसे फ़ंक्शन हैं जिनमें एक डोमेन होता है X∩Y.

यह इस प्रकार है कि n चर के कार्य जो हर जगह परिभाषित होते हैं और n चर के कार्य जो किसी दिए गए बिंदु के कुछ पड़ोस (गणित) में परिभाषित होते हैं, दोनों वास्तविक (ℝ-बीजगणित) पर क्रमविनिमेय बीजगणित (संरचना) बनाते हैं।

कोई इसी प्रकार परिभाषित कर सकता है $1/f:(x)\mapsto 1/f(x),$ जो केवल बिंदुओं के समुच्चय होने पर ही एक फलन है (x) f के डोमेन में ऐसा है कि f(x) ≠ 0 में ℝ का एक खुला उपसमुच्चय शामिल है। इस बाधा का तात्पर्य है कि उपरोक्त दो बीजगणित क्षेत्र (गणित) नहीं हैं।

निरंतरता और सीमा

किसी वास्तविक चर के वास्तविक फलन की सीमा।

19वीं सदी के दूसरे भाग तक गणितज्ञों द्वारा केवल सतत फलनों पर ही विचार किया जाता था। उस समय, टोपोलॉजिकल स्पेस की औपचारिक परिभाषा और टोपोलॉजिकल स्पेस के बीच एक सतत मानचित्र से काफी पहले एक या कई वास्तविक चर के कार्यों के लिए निरंतरता की धारणा को विस्तृत किया गया था। चूंकि वास्तविक चर के निरंतर कार्य गणित में सर्वव्यापी हैं, इसलिए टोपोलॉजिकल स्पेस के बीच निरंतर मानचित्रों की सामान्य धारणा के संदर्भ के बिना इस धारणा को परिभाषित करना उचित है।

निरंतरता को परिभाषित करने के लिए, ℝ के दूरी फ़ंक्शन पर विचार करना उपयोगी है, जो 2 वास्तविक चर का हर जगह परिभाषित फ़ंक्शन है: $d(x,y)=|x-y|$ एक फ़ंक्शन f एक बिंदु पर 'निरंतर' है $a$ जो प्रत्येक सकारात्मक वास्तविक संख्या के लिए, अपने डोमेन का आंतरिक (टोपोलॉजी) है ε, एक धनात्मक वास्तविक संख्या है φ ऐसा है कि $|f(x)-f(a)|<\varepsilon$ सभी के लिए $x$ ऐसा है कि $d(x,a)<\varphi .$ दूसरे शब्दों में, φ को त्रिज्या के अंतराल के f द्वारा छवि प्राप्त करने के लिए पर्याप्त छोटा चुना जा सकता है φ पर केन्द्रित $a$ लंबाई के अंतराल में निहित है 2ε पर केन्द्रित $f(a).$ कोई फलन सतत है यदि वह अपने डोमेन के प्रत्येक बिंदु पर सतत है।

एक वास्तविक चर के वास्तविक-मूल्यवान फलन की सीमा (गणित) इस प्रकार है। मान लीजिए a फ़ंक्शन f के डोमेन X के समापन (टोपोलॉजी) में एक बिंदु है। फ़ंक्शन, f की एक सीमा L होती है जब x, a की ओर झुकता है, जिसे दर्शाया जाता है

$L=\lim _{x\to a}f(x),$

यदि निम्नलिखित शर्त पूरी होती है: प्रत्येक सकारात्मक वास्तविक संख्या ε > 0 के लिए, एक सकारात्मक वास्तविक संख्या δ > 0 होती है

$|f(x)-L|<\varepsilon$

डोमेन में सभी x के लिए ऐसा है

$d(x,a)<\delta .$

यदि सीमा मौजूद है, तो यह अद्वितीय है। यदि a डोमेन के आंतरिक भाग में है, तो सीमा तभी मौजूद होती है जब फ़ंक्शन a पर निरंतर होता है। इस मामले में, हमारे पास है

$f(a)=\lim _{x\to a}f(x).$

जब a, f के डोमेन की सीमा (टोपोलॉजी) में है, और यदि f की a पर सीमा है, तो बाद वाला सूत्र निरंतरता द्वारा f के डोमेन को a तक विस्तारित करने की अनुमति देता है।

कैलकुलस

मान लीजिए, कोई वास्तविक चर के कई फ़ंक्शन एकत्र कर सकता है

$y_{1}=f_{1}(x)\,,\quad y_{2}=f_{2}(x)\,,\ldots ,y_{n}=f_{n}(x)$

x द्वारा पैरामीट्रिज्ड एक वेक्टर में:

$\mathbf {y} =(y_{1},y_{2},\ldots ,y_{n})=[f_{1}(x),f_{2}(x),\ldots ,f_{n}(x)]$

वेक्टर y का व्युत्पन्न f का वेक्टर व्युत्पन्न है_i(x) i = 1, 2, ..., n के लिए:

${\frac {d\mathbf {y} }{dx}}=\left({\frac {dy_{1}}{dx}},{\frac {dy_{2}}{dx}},\ldots ,{\frac {dy_{n}}{dx}}\right)$

वेरिएबल x के संबंध में एकीकरण करके, स्थिति वेक्टर 'r' = 'r'(x) के साथ, x द्वारा पैरामीट्रिज़ किए गए अंतरिक्ष वक्र के साथ लाइन इंटीग्रल भी किया जा सकता है:

$\int _{a}^{b}\mathbf {y} (x)\cdot d\mathbf {r} =\int _{a}^{b}\mathbf {y} (x)\cdot {\frac {d\mathbf {r} (x)}{dx}}dx$

जहां · डॉट उत्पाद है, और x = a और x = b वक्र के प्रारंभ और अंत बिंदु हैं।

प्रमेय

एकीकरण और डेरिवेटिव की परिभाषाओं के साथ, प्रमुख प्रमेय तैयार किए जा सकते हैं, जिसमें कैलकुलस के मौलिक प्रमेय, भागों द्वारा एकीकरण और टेलर के प्रमेय शामिल हैं। अभिन्न चिह्न के तहत प्रमेय विभेदन का उपयोग करके अभिन्न और व्युत्पन्न के मिश्रण का मूल्यांकन किया जा सकता है।

अंतर्निहित कार्य

किसी वास्तविक चर का वास्तविक-मूल्यवान अंतर्निहित फ़ंक्शन y = f(x) के रूप में नहीं लिखा जाता है। इसके बजाय, मैपिंग स्पेस ℝ से है^{ℝ में शून्य तत्व के लिए 2} (सिर्फ सामान्य शून्य 0):

$\phi :\mathbb {R} ^{2}\to \{0\}$

और

$\phi (x,y)=0$

चरों में एक समीकरण है. अंतर्निहित फ़ंक्शंस फ़ंक्शंस का प्रतिनिधित्व करने का एक अधिक सामान्य तरीका है, क्योंकि यदि:

$y=f(x)$

तो हम हमेशा परिभाषित कर सकते हैं:

$\phi (x,y)=y-f(x)=0$

लेकिन इसका विपरीत हमेशा संभव नहीं होता है, यानी सभी अंतर्निहित कार्यों में इस समीकरण का रूप नहीं होता है।

ℝ में एक-आयामी अंतरिक्ष वक्रⁿ

3डी में अंतरिक्ष वक्र। स्थिति वेक्टर r को एक अदिश t द्वारा परिचालित किया जाता है। r = a पर लाल रेखा वक्र की स्पर्शरेखा है, और नीला तल वक्र के अभिलम्बवत् है।

सूत्रीकरण

कार्यों को देखते हुए r₁ = r₁(t), r₂ = r₂(t), ..., r_n = r_n(t) सभी एक सामान्य चर t, ताकि:

${\begin{aligned}r_{1}:\mathbb {R} \rightarrow \mathbb {R} &\quad r_{2}:\mathbb {R} \rightarrow \mathbb {R} &\cdots &\quad r_{n}:\mathbb {R} \rightarrow \mathbb {R} \\r_{1}=r_{1}(t)&\quad r_{2}=r_{2}(t)&\cdots &\quad r_{n}=r_{n}(t)\\\end{aligned}}$

या एक साथ लिया गया:

$\mathbf {r} :\mathbb {R} \rightarrow \mathbb {R} ^{n}\,,\quad \mathbf {r} =\mathbf {r} (t)$

फिर पैरामीट्रिज्ड एन-ट्यूपल,

$\mathbf {r} (t)=[r_{1}(t),r_{2}(t),\ldots ,r_{n}(t)]$

एक आयामी अंतरिक्ष वक्र का वर्णन करता है।

वक्र पर स्पर्श रेखा

एक बिंदु पर r(t = c) = a = (a₁, a₂, ..., a_n) कुछ स्थिरांक t = c के लिए, उस बिंदु पर वक्र की एक-आयामी स्पर्श रेखा के समीकरण r के सामान्य व्युत्पन्न के संदर्भ में दिए गए हैं₁(टी), आर₂(टी), ..., आर_n(टी), और आर टी के संबंध में:

${\frac {r_{1}(t)-a_{1}}{dr_{1}(t)/dt}}={\frac {r_{2}(t)-a_{2}}{dr_{2}(t)/dt}}=\cdots ={\frac {r_{n}(t)-a_{n}}{dr_{n}(t)/dt}}$

वक्र के लिए सामान्य तल

'आर' = 'ए' पर स्पर्शरेखा रेखा के सामान्य एन-आयामी हाइपरप्लेन का समीकरण है:

$(p_{1}-a_{1}){\frac {dr_{1}(t)}{dt}}+(p_{2}-a_{2}){\frac {dr_{2}(t)}{dt}}+\cdots +(p_{n}-a_{n}){\frac {dr_{n}(t)}{dt}}=0$

या डॉट उत्पाद के संदर्भ में:

$(\mathbf {p} -\mathbf {a} )\cdot {\frac {d\mathbf {r} (t)}{dt}}=0$

कहाँ p = (p₁, p₂, ..., p_n) समतल में बिंदु हैं, अंतरिक्ष वक्र पर नहीं।

गतिकी से संबंध

शास्त्रीय कण की गतिक मात्राएँ: द्रव्यमान m, स्थिति 'r', वेग 'v', त्वरण 'a'।

डी'आर'(टी)/डीटी की भौतिक और ज्यामितीय व्याख्या पथ 'आर'(टी) के साथ चलने वाले एक बिंदु जैसे कण का वेग है, जो 'आर' को स्थानिक स्थिति वेक्टर के रूप में मानता है जो समय टी द्वारा पैरामीट्रिज्ड समन्वयित होता है, और गति की तात्कालिक दिशा में सभी t के लिए अंतरिक्ष वक्र की स्पर्श रेखा है। टी = सी पर, अंतरिक्ष वक्र में एक स्पर्शरेखा वेक्टर होता है dr(t)/dt|_{t = c}, और t = c पर अंतरिक्ष वक्र के लिए सामान्य हाइपरप्लेन भी t = c पर स्पर्शरेखा के लिए सामान्य है। इस तल में कोई भी सदिश ('p' − 'a') सामान्य होना चाहिए dr(t)/dt|_{t = c}.

इसी प्रकार, डी²r(t)/dt²कण का त्वरण है, और वक्रता त्रिज्या (गणित) के साथ निर्देशित वक्र के लिए सामान्य वेक्टर है।

मैट्रिक्स मूल्यवान फ़ंक्शन

एक मैट्रिक्स (गणित) एकल चर का एक फ़ंक्शन भी हो सकता है। उदाहरण के लिए, 2d में रोटेशन मैट्रिक्स:

$R(\theta )={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}$

मूल के चारों ओर घूर्णन कोण का एक मैट्रिक्स मान फ़ंक्शन है। इसी प्रकार, विशेष सापेक्षता में, शुद्ध बढ़ावा के लिए लोरेंत्ज़ परिवर्तन मैट्रिक्स (रोटेशन के बिना):

$\Lambda (\beta )={\begin{bmatrix}{\frac {1}{\sqrt {1-\beta ^{2}}}}&-{\frac {\beta }{\sqrt {1-\beta ^{2}}}}&0&0\\-{\frac {\beta }{\sqrt {1-\beta ^{2}}}}&{\frac {1}{\sqrt {1-\beta ^{2}}}}&0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}}$

बूस्ट पैरामीटर β = v/c का एक फ़ंक्शन है, जिसमें v संदर्भ के फ्रेम (एक सतत चर) के बीच सापेक्ष वेग है, और c प्रकाश की गति, एक स्थिरांक है।

बैनाच और हिल्बर्ट स्थान और क्वांटम यांत्रिकी

पिछले अनुभाग को सामान्यीकृत करते हुए, वास्तविक चर के फ़ंक्शन का आउटपुट बानाच स्पेस या हिल्बर्ट स्पेस में भी हो सकता है। इन स्थानों में, विभाजन और गुणा और सीमाएं सभी परिभाषित हैं, इसलिए व्युत्पन्न और अभिन्न जैसी धारणाएं अभी भी लागू होती हैं। यह विशेष रूप से क्वांटम यांत्रिकी में अक्सर होता है, जहां कोई ब्रा-केट नोटेशन या ऑपरेटर (भौतिकी) का व्युत्पन्न लेता है। उदाहरण के लिए, सामान्य समय-निर्भर श्रोडिंगर समीकरण में ऐसा होता है:

$i\hbar {\frac {\partial }{\partial t}}\Psi ={\hat {H}}\Psi$

जहां कोई तरंग फ़ंक्शन का व्युत्पन्न लेता है, जो कई अलग-अलग हिल्बर्ट स्थानों का एक तत्व हो सकता है।

वास्तविक चर का जटिल-मूल्यवान फ़ंक्शन

एक वास्तविक चर के एक जटिल-मूल्य वाले फ़ंक्शन को वास्तविक-मूल्य वाले कार्यों की परिभाषा में आराम देकर, वास्तविक संख्याओं के लिए कोडोमेन के प्रतिबंध और जटिल संख्या मानों की अनुमति देकर परिभाषित किया जा सकता है।

अगर f(x) एक ऐसा जटिल मूल्यवान फ़ंक्शन है, इसे इस प्रकार विघटित किया जा सकता है

f(x) = g(x) + ih(x),

कहाँ g और h वास्तविक-मूल्यवान कार्य हैं। दूसरे शब्दों में, जटिल मूल्यवान कार्यों का अध्ययन आसानी से वास्तविक मूल्यवान कार्यों के जोड़े के अध्ययन को कम कर देता है।

एक वास्तविक चर के कार्यों के सेट की प्रमुखता

वास्तविक चर के वास्तविक-मूल्यवान कार्यों के सेट की प्रमुखता, $\mathbb {R} ^{\mathbb {R} }=\{f:\mathbb {R} \to \mathbb {R} \}$, है $\beth _{2}=2^{\mathfrak {c}}$, जो कॉन्टिनम (सेट सिद्धांत) (यानी, सभी वास्तविक संख्याओं का सेट) की कार्डिनैलिटी से सख्ती से बड़ा है। इस तथ्य को कार्डिनल अंकगणित द्वारा आसानी से सत्यापित किया जाता है:

$$\mathrm {card} (\mathbb {R} ^{\mathbb {R} })=\mathrm {card} (\mathbb {R} )^{\mathrm {card} (\mathbb {R} )}={\mathfrak {c}}^{\mathfrak {c}}=(2^{\aleph _{0}})^{\mathfrak {c}}=2^{\aleph _{0}\cdot {\mathfrak {c}}}=2^{\mathfrak {c}}.$$

इसके अलावा, यदि $X$ एक सेट ऐसा है $2\leq \mathrm {card} (X)\leq {\mathfrak {c}}$, फिर सेट की कार्डिनैलिटी $X^{\mathbb {R} }=\{f:\mathbb {R} \to X\}$ ई आल्सो $2^{\mathfrak {c}}$, तब से

$$2^{\mathfrak {c}}=\mathrm {card} (2^{\mathbb {R} })\leq \mathrm {card} (X^{\mathbb {R} })\leq \mathrm {card} (\mathbb {R} ^{\mathbb {R} })=2^{\mathfrak {c}}.$$

हालाँकि, निरंतर कार्यों का सेट $C^{0}(\mathbb {R} )=\{f:\mathbb {R} \to \mathbb {R} :f\ \mathrm {continuous} \}$ इसमें सख्ती से छोटी कार्डिनलिटी है, सातत्य की कार्डिनैलिटी, ${\mathfrak {c}}$. यह इस तथ्य से पता चलता है कि एक सतत फ़ंक्शन पूरी तरह से उसके डोमेन के घने उपसमुच्चय पर उसके मूल्य से निर्धारित होता है। इस प्रकार, वास्तविकताओं पर निरंतर वास्तविक-मूल्यवान कार्यों के सेट की कार्डिनैलिटी एक तर्कसंगत चर के वास्तविक-मूल्यवान कार्यों के सेट की कार्डिनैलिटी से अधिक नहीं है। कार्डिनल अंकगणित द्वारा:

$$\mathrm {card} (C^{0}(\mathbb {R} ))\leq \mathrm {card} (\mathbb {R} ^{\mathbb {Q} })=(2^{\aleph _{0}})^{\aleph _{0}}=2^{\aleph _{0}\cdot \aleph _{0}}=2^{\aleph _{0}}={\mathfrak {c}}.$$

दूसरी ओर, चूँकि बीच में स्पष्ट आपत्ति है $\mathbb {R}$ और निरंतर कार्यों का सेट $\{f:\mathbb {R} \to \mathbb {R} :f(x)\equiv x_{0}\}$, जो एक उपसमुच्चय बनाता है $C^{0}(\mathbb {R} )$, $\mathrm {card} (C^{0}(\mathbb {R} ))\geq {\mathfrak {c}}$ भी धारण करना चाहिए. इस तरह, $\mathrm {card} (C^{0}(\mathbb {R} ))={\mathfrak {c}}$.

यह भी देखें

• वास्तविक विश्लेषण
• कई वास्तविक चरों का कार्य
• जटिल विश्लेषण
• कई जटिल चरों का कार्य

संदर्भ

• F. Ayres, E. Mendelson (2009). Calculus. Schaum's outline series (5th ed.). McGraw Hill. ISBN 978-0-07-150861-2.
• R. Wrede, M. R. Spiegel (2010). Advanced calculus. Schaum's outline series (3rd ed.). McGraw Hill. ISBN 978-0-07-162366-7.
• N. Bourbaki (2004). Functions of a Real Variable: Elementary Theory. Springer. ISBN 354-065-340-6.

बाहरी संबंध

• Multivariable Calculus
• L. A. Talman (2007) Differentiability for Multivariable Functions