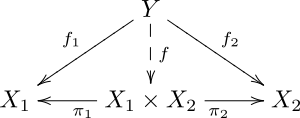Difference between revisions of "क्रमित युग्म"
Rani Kumari (talk | contribs) |
|||
| (29 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
: | |||
{{short description|Pair of mathematical objects}} | {{short description|Pair of mathematical objects}} | ||
[[File:Ellipse in coordinate system with semi-axes labelled.svg|thumb|300px|[[विश्लेषणात्मक ज्यामिति]] [[यूक्लिडियन विमान]] में प्रत्येक बिंदु को एक | [[File:Ellipse in coordinate system with semi-axes labelled.svg|thumb|300px|[[विश्लेषणात्मक ज्यामिति]] [[यूक्लिडियन विमान]] में प्रत्येक बिंदु को एक क्रमित युग्मों से जोड़ती है। लाल दीर्घवृत्त सभी युग्मों (x, y) के समुच्चय से जुड़ा है जैसे कि {{sfrac|''x''<sup>2</sup>|4}}+y<sup>2</sup>=1.]]गणित में, '''[[क्रम|क्रमित]] युग्म''' (''a'', ''b'') वस्तुओं का युग्म है। जिस क्रम में वस्तुएं दिखाई देती हैं वह महत्वपूर्ण है क्रमित युग्म (''a'', ''b'') क्रमित युग्म (''b'', ''a'') से भिन्न है जब तक' '''a''<nowiki/>' = '<nowiki/>''b''<nowiki/>' न हो। (इसके विपरीत, अव्यवस्थित युग्म {''a'', ''b''} अव्यवस्थित युग्म {''b'', ''a''} के बराबर होती है।) | ||
क्रमित युग्मों को 2-टुपल्स, या अनुक्रम (कभी-कभी, कंप्यूटर विज्ञान के संदर्भ में सूचियाँ) भी कहा जाता है जिनकी लंबाई 2 होती है। [[अदिश (गणित)|अदिशों]] के क्रमित युग्मों को कभी-कभी 2-आयामी [[वेक्टर (गणित और भौतिकी)|सदिश]] कहा जाता है। | |||
(तकनीकी रूप से, यह [[शब्दावली]] का अनुचित उपयोग है क्योंकि क्रमित युग्मों को [[सदिश स्थल]] का तत्व नहीं होना चाहिए।) क्रमित युग्मों की प्रविष्टियां अन्य क्रमित युग्म हो सकते हैं, जो क्रमित ''एन'' -ट्यूपल्स (''n'' वस्तुओं की क्रमबद्ध सूचियां) की पुनरावर्ती परिभाषा को सक्षम करते हैं। उदाहरण के लिए, क्रमित ट्रिपल (''a'', ''b'', c) को (''a'', (''b'',''c'')) के रूप में परिभाषित किया जा सकता है, अर्थात, एक युग्म दूसरे में स्थिर है। | |||
[[कार्तीय गुणन]] | क्रमित युग्म (''a'', ''b'') में, वस्तु ''a'' को ''पहली प्रवेश'' कहा जाता है, और वस्तु ''b'' को युग्म की ''दूसरी प्रवेश'' कहलाती है। वैकल्पिक रूप से, वस्तुओं को पहले और दूसरे ''घटक'', पहले और दूसरे ''निर्देशांक'', या क्रमित युग्म के बाएं और दाएं ''अनुमान'' कहा जाता है। | ||
[[कार्तीय गुणन|कार्तीय गुणनफल]] और [[द्विआधारी संबंध]] (और इसलिए फलन) क्रमित युग्मों के रूप में परिभाषित किए गए हैं, चित्र में। | |||
== सामान्यता == | == सामान्यता == | ||
माना <math>(a_1, b_1)</math> तथा <math>(a_2, b_2)</math> युग्मों का आदेश दिया जाए। फिर क्रमित युग्मों की विशेषता (या परिभाषित) है | |||
:<math>(a_1, b_1) = (a_2, b_2)\text{ if and only if } a_1 = a_2\text{ and }b_1 = b_2.</math> | :<math>(a_1, b_1) = (a_2, b_2)\text{ if and only if } a_1 = a_2\text{ and }b_1 = b_2.</math> | ||
सभी क्रमित युग्मों का समुच्चय (गणित) जिसकी पहली प्रविष्टि किसी समुच्चय A में है और जिसकी दूसरी प्रविष्टि किसी समुच्चय B में है, A और B का कार्तीय गुणन कहलाता है, और A × B लिखा जाता है। समुच्चय A और B के बीच एक द्विआधारी संबंध A × B का उपसमुच्चय है। | सभी क्रमित युग्मों का समुच्चय (गणित) जिसकी पहली प्रविष्टि किसी समुच्चय A में है और जिसकी दूसरी प्रविष्टि किसी समुच्चय B में है, A और B का कार्तीय गुणन कहलाता है, और A × B लिखा जाता है। समुच्चय A और B के बीच एक द्विआधारी संबंध A × B का उपसमुच्चय है। | ||
< | {{math|(''a'', ''b'')}} संकेत चिन्ह का उपयोग अन्य उद्देश्यों के लिए किया जा सकता है, विशेष रूप से [[वास्तविक संख्या रेखा]] पर खुले अंतराल को दर्शाने के रूप में ऐसी स्थितियों में, संदर्भ प्रायः यह स्पष्ट कर देगा कि कौन सा अर्थ अभीष्ट है।<ref>{{citation|first=Steven R.|last=Lay|title=Analysis / With an Introduction to Proof|edition=4th|publisher=Pearson / Prentice Hall|isbn=978-0-13-148101-5|year=2005|page=50}}</ref><ref>{{citation|first=Keith|last=Devlin|title=Sets, Functions and Logic / An Introduction to Abstract Mathematics|edition=3rd|publisher=Chapman & Hall / CRC|year=2004|isbn=978-1-58488-449-1|page=79}}</ref> अतिरिक्त स्पष्टीकरण के लिए, क्रमित युग्मों को भिन्न संकेत चिन्ह द्वारा दर्शाया जा सकता है <math display="inline"> \langle a,b\rangle</math>, परंतु इस संकेत चिन्ह के अन्य उपयोग भी हैं। | ||
ऐसे संदर्भों में जहां मनमाने ढंग से एन-टुपल्स पर विचार किया जाता है, {{pi}}{{su|p=''n''|b=''i''}}(टी) एन-ट्यूपल टी के आई-वें घटक के लिए एक | युग्म p के बाएँ और दाएँ प्रक्षेपण को प्रायः क्रमशः {{pi}}<sub>1</sub>(p) और {{pi}}<sub>2</sub>(p), या {{pi}}<sub>''ℓ''</sub>(p) और {{pi}}<sub>''r''</sub>(p), द्वारा निरूपित किया जाता है क्रमशः ऐसे संदर्भों में जहां मनमाने ढंग से एन-टुपल्स पर विचार किया जाता है, {{pi}}{{su|p=''n''|b=''i''}}(टी) एन-ट्यूपल टी के आई-वें घटक के लिए एक सामान्य संकेत है। | ||
== अनौपचारिक और औपचारिक परिभाषाएँ == | == अनौपचारिक और औपचारिक परिभाषाएँ == | ||
कुछ परिचयात्मक गणित की पाठ्यपुस्तकों में क्रमबद्ध युग्म की एक अनौपचारिक (या सहज) परिभाषा दी गई है, | कुछ परिचयात्मक गणित की पाठ्यपुस्तकों में क्रमबद्ध युग्म की एक अनौपचारिक (या सहज) परिभाषा दी गई है, | ||
किन्हीं दो वस्तुओं के लिए {{mvar|a}} तथा {{mvar|b}}, | जैसे किन्हीं भी दो वस्तुओं के लिए {{mvar|a}} तथा {{mvar|b}} के लिए, क्रमित युग्म {{math|(''a'', ''b'')}} उस क्रम में दो वस्तुओं {{mvar|a}} तथा {{mvar|b}} को निर्दिष्ट करने वाला संकेत चिन्ह है।<ref name="Wolf">{{citation|first=Robert S.|last=Wolf|title=Proof, Logic, and Conjecture / The Mathematician's Toolbox|publisher=W. H. Freeman and Co.|year=1998|isbn=978-0-7167-3050-7|page=164}}</ref> | ||
इसके बाद | इसके बाद प्रायः दो तत्वों के एक समुच्चय की तुलना की जाती है, यह संकेत करते हुए कि एक समुच्चय में {{mvar|a}} तथा {{mvar|b}} अलग होना चाहिए, लेकिन एक क्रमित युग्मों में वे समान हो सकते हैं और जबकि एक समुच्चय के तत्वों को सूचीबद्ध करने का क्रम मायने नहीं रखता है, क्रमित युग्मों में अलग-अलग प्रविष्टियों के क्रम को बदलने से क्रमित युग्म बदल जाती है। | ||
यह परिभाषा असंतोषजनक है क्योंकि यह केवल वर्णनात्मक है और आदेश की सहज समझ पर आधारित है। हालांकि, जैसा कि कभी-कभी बताया गया है, इस विवरण पर भरोसा करने से कोई नुकसान नहीं होगा और लगभग हर कोई इस तरीके से | यह "परिभाषा" असंतोषजनक है क्योंकि यह केवल वर्णनात्मक है और आदेश की सहज समझ पर आधारित है। हालांकि, जैसा कि कभी-कभी बताया गया है, इस विवरण पर भरोसा करने से कोई नुकसान नहीं होगा और लगभग हर कोई इस तरीके से क्रमित युग्मों के बारे में सोचता है।<ref>{{citation|first1=Peter|last1=Fletcher|first2=C. Wayne|last2=Patty|title=Foundations of Higher Mathematics|publisher=PWS-Kent|year=1988|isbn=0-87150-164-3|page=80}}</ref> | ||
अधिक संतोषजनक दृष्टिकोण यह देखना है कि गणित में क्रमित युग्मों की भूमिका को समझने के लिए ऊपर दिए गए क्रमित युग्मों के चारित्रिक गुणों की आवश्यकता है। इसलिए क्रमित युग्म को एक [[आदिम धारणा]] के रूप में लिया जा सकता है, जिसका संबद्ध अभिगृहीत अभिलाक्षणिक गुण है। यह निकोलस बॉरबाकी द्वारा लिया गया दृष्टिकोण था। यह 1954 में प्रकाशित अपने समुच्चय का सिद्धांत में एन.बॉरबाकी समूह द्वारा लिया गया। हालांकि, इस दृष्टिकोण में इसकी कमियां भी हैं क्योंकि क्रमित युग्मों के अस्तित्व और उनकी विशिष्ट संपत्ति दोनों को स्वयंसिद्ध रूप से ग्रहण किया जाना चाहिए।<ref name="Wolf" /> | |||
क्रमित युग्मों से सख्ती से व्यवहार का एक और तरीका उन्हें समुच्चय सिद्धांत के संदर्भ में औपचारिक रूप से परिभाषित करना है। यह कई तरीकों से किया जा सकता है और इसका लाभ यह है कि समुच्चय सिद्धांत को परिभाषित करने वाले स्वयंसिद्धों से अस्तित्व और विशिष्ट संपत्ति को सिद्ध किया जा सकता है। इस परिभाषा के सबसे उद्धृत संस्करणों में से एक कुराटोव्स्की (नीचे देखें) के कारण है और उनकी परिभाषा का उपयोग 1970 में प्रकाशित बॉरबाकी के थ्योरी ऑफ़ सेट्स के दूसरे संस्करण में किया गया था। यहां तक कि उन गणितीय पाठ्यपुस्तकों में भी जो क्रमित युग्मों की अनौपचारिक परिभाषा देती हैं अभ्यास में कुराटोस्की की औपचारिक परिभाषा का उल्लेख कीजिए। | |||
यदि कोई इस बात से सहमत है कि | == [[समुच्चय सिद्धान्त]] का उपयोग करते हुए क्रमित युग्म को परिभाषित करना == | ||
यदि कोई इस बात से सहमत है कि समुच्चय सिद्धांत गणित की एक आकर्षक नींव है, तो सभी गणितीय वस्तुओं को किसी प्रकार के समुच्चय (गणित) के रूप में परिभाषित किया जाना चाहिए। इसलिए यदि क्रमित युग्म प्राथमिक के रूप में नहीं लिया जाता है, तो इसे समुच्चय के रूप में परिभाषित किया जाना चाहिए।<ref>[[Willard van Orman Quine|Quine]] has argued that the set-theoretical implementations of the concept of the ordered pair is a paradigm for the clarification of philosophical ideas (see "[[Word and Object]]", section 53). | |||
The general notion of such definitions or implementations are discussed in Thomas Forster "Reasoning about theoretical entities". | The general notion of such definitions or implementations are discussed in Thomas Forster "Reasoning about theoretical entities". | ||
</ref> | </ref> क्रमित युग्मों की कई समुच्चय-सैद्धांतिक परिभाषाएँ नीचे दी गई हैं (यह भी देखें <ref>{{Cite web|last=Dipert|first=Randall|title=क्रमबद्ध जोड़े के सेट-सैद्धांतिक प्रतिनिधित्व और संबंधों के तर्क के लिए उनकी पर्याप्तता।|url=https://www.academia.edu/|url-status=live}}</ref>). | ||
===वीनर की परिभाषा=== | ===वीनर की परिभाषा=== | ||
[[नॉर्बर्ट वीनर]] ने 1914 में | [[नॉर्बर्ट वीनर]] ने 1914 में क्रमित युग्मों की पहली समुच्चय सैद्धांतिक परिभाषा प्रस्तावित की<ref>Wiener's paper "A Simplification of the logic of relations" is reprinted, together with a valuable commentary on pages 224ff in van Heijenoort, Jean (1967), ''From Frege to Gödel: A Source Book in Mathematical Logic, 1979–1931'', Harvard University Press, Cambridge MA, {{isbn|0-674-32449-8}} (pbk.). van Heijenoort states the simplification this way: "By giving a definition of the ordered pair of two elements in terms of class operations, the note reduced the theory of relations to that of classes".</ref> | ||
:<math>\left( a, b \right) := | :<math>\left( a, b \right) := | ||
\left\{\left\{ \left\{a\right\},\, \emptyset \right\},\, \left\{\left\{b\right\}\right\}\right\}.</math> | \left\{\left\{ \left\{a\right\},\, \emptyset \right\},\, \left\{\left\{b\right\}\right\}\right\}.</math> | ||
उन्होंने देखा कि इस परिभाषा ने [[गणितीय सिद्धांत]] के [[प्रकार सिद्धांत]] को | उन्होंने देखा कि इस परिभाषा ने [[गणितीय सिद्धांत]] के [[प्रकार सिद्धांत]] को समुच्चय के रूप में परिभाषित करना संभव बना दिया। गणितीय सिद्धांत ने आदिम धारणा के रूप में , और इसलिए सभी अर्थों का [[संबंध (गणित)|संबंध]] लिया था। | ||
वीनर ने <nowiki> | वीनर ने प्रकार सिद्धांत के साथ परिभाषा को संगत बनाने के लिए {''b''<nowiki>} के बजाय {{</nowiki>''b''<nowiki>}} का इस्तेमाल किया, जहां वर्ग में सभी तत्व समान "प्रकार" के होने चाहिए। एक अतिरिक्त समुच्चय के भीतर नेस्टेड, </nowiki>''b'' के साथ,इसका प्रकार <math>\{\{a\}, \emptyset\}</math>'s के बराबर है। | ||
=== | === हॉसडॉर्फ की परिभाषा === | ||
लगभग उसी समय वीनर (1914) के रूप में, [[फेलिक्स हॉसडॉर्फ]] ने अपनी परिभाषा प्रस्तावित की | लगभग उसी समय वीनर (1914) के रूप में, [[फेलिक्स हॉसडॉर्फ]] ने अपनी परिभाषा प्रस्तावित की | ||
: <math>(a, b) := \left\{ \{a, 1\}, \{b, 2\} \right\}</math> | : <math>(a, b) := \left\{ \{a, 1\}, \{b, 2\} \right\}</math> | ||
जहाँ 1 और 2 a और b से भिन्न | "जहाँ 1 और 2 दो अलग-अलग वस्तुएँ हैं जो a और b से भिन्न हैं।<ref>cf introduction to Wiener's paper in van Heijenoort 1967:224</ref> | ||
=== कुराटोस्की की परिभाषा === | === कुराटोस्की की परिभाषा === | ||
1921 में [[काज़िमिर्ज़ कुराटोव्स्की]] ने अब स्वीकृत परिभाषा की पेशकश की<ref>cf introduction to Wiener's paper in van Heijenoort 1967:224. van Heijenoort observes that the resulting set that represents the ordered pair "has a type higher by 2 than the elements (when they are of the same type)"; he offers references that show how, under certain circumstances, the type can be reduced to 1 or 0.</ref><ref>{{cite journal|title=सेट थ्योरी में आदेश की धारणा पर|first=Casimir|last=Kuratowski|author-link=Kazimierz Kuratowski|year=1921|journal=[[Fundamenta Mathematicae]]|pages=161–171|volume=2|number=1|doi=10.4064/fm-2-1-161-171|url=http://matwbn.icm.edu.pl/ksiazki/fm/fm2/fm2122.pdf|access-date=2013-05-29|archive-url=https://web.archive.org/web/20190429103938/http://matwbn.icm.edu.pl/ksiazki/fm/fm2/fm2122.pdf|archive-date=2019-04-29|url-status=dead|doi-access=free}}</ref> | 1921 में [[काज़िमिर्ज़ कुराटोव्स्की]] ने क्रमित युग्मों (a, b) अब स्वीकृत परिभाषा की पेशकश की<ref>cf introduction to Wiener's paper in van Heijenoort 1967:224. van Heijenoort observes that the resulting set that represents the ordered pair "has a type higher by 2 than the elements (when they are of the same type)"; he offers references that show how, under certain circumstances, the type can be reduced to 1 or 0.</ref><ref>{{cite journal|title=सेट थ्योरी में आदेश की धारणा पर|first=Casimir|last=Kuratowski|author-link=Kazimierz Kuratowski|year=1921|journal=[[Fundamenta Mathematicae]]|pages=161–171|volume=2|number=1|doi=10.4064/fm-2-1-161-171|url=http://matwbn.icm.edu.pl/ksiazki/fm/fm2/fm2122.pdf|access-date=2013-05-29|archive-url=https://web.archive.org/web/20190429103938/http://matwbn.icm.edu.pl/ksiazki/fm/fm2/fm2122.pdf|archive-date=2019-04-29|url-status=dead|doi-access=free}}</ref> | ||
:<math>(a, \ b)_K \; := \ \{ \{ a \}, \ \{ a, \ b \} \}.</math> | :<math>(a, \ b)_K \; := \ \{ \{ a \}, \ \{ a, \ b \} \}.</math> | ||
ध्यान दें कि इस परिभाषा का उपयोग तब भी किया जाता है जब पहले और दूसरे निर्देशांक समान हों | ध्यान दें कि इस परिभाषा का उपयोग तब भी किया जाता है जब पहले और दूसरे निर्देशांक समान हों | ||
: <math>(x,\ x)_K = \{\{x\},\{x, \ x\}\} = \{\{x\},\ \{x\}\} = \{\{x\}\}</math> | : <math>(x,\ x)_K = \{\{x\},\{x, \ x\}\} = \{\{x\},\ \{x\}\} = \{\{x\}\}</math> | ||
कुछ क्रमित युग्म p को देखते हुए, गुण x, p का पहला निर्देशांक है, इस प्रकार तैयार किया जा सकता है | कुछ क्रमित युग्म p को देखते हुए, गुण "x, p का पहला निर्देशांक है", इस प्रकार तैयार किया जा सकता है | ||
:<math>\forall Y\in p:x\in Y.</math> | :<math>\forall Y\in p:x\in Y.</math> | ||
संपत्ति x p का दूसरा निर्देशांक है जिसे इस प्रकार तैयार किया जा सकता है | संपत्ति "x p का दूसरा निर्देशांक है" जिसे इस प्रकार तैयार किया जा सकता है | ||
इस मामले में | <math>(\exist Y\in p:x\in Y)\land(\forall Y_1,Y_2\in p:Y_1\ne Y_2\rarr (x\notin Y_1\lor x \notin Y_2)).</math> | ||
इस मामले में बाएँ और दाएँ निर्देशांक समान हैं, दाएँ संयोजन | |||
यह है कि हम एक | <math>(\forall Y_1,Y_2\in p:Y_1\ne Y_2\rarr (x\notin Y_1 \lor x \notin Y_2))</math> निरर्थक रूप से सत्य है, क्योंकि ''Y''<sub>1</sub> ≠ ''Y''<sub>2</sub> ऐसा कभी नहीं होता। | ||
यह है कि हम एक युग्म के पहले समन्वय को कैसे निकाल सकते हैं (एकपक्षीय प्रतिच्छेदन और एकपक्षीय मिलन के लिए पुनरावृत्त-संचालन संकेत चिन्ह का उपयोग करके) | |||
:<math>\pi_1(p) = \bigcup\bigcap p.</math> | :<math>\pi_1(p) = \bigcup\bigcap p.</math> | ||
इस प्रकार दूसरा निर्देशांक निकाला जा सकता है | इस प्रकार दूसरा निर्देशांक निकाला जा सकता है | ||
:<math>\pi_2(p) = \bigcup\left\{\left. x \in \bigcup p\,\right|\,\bigcup p \neq \bigcap p \rarr x \notin \bigcap p \right\}.</math> | :<math>\pi_2(p) = \bigcup\left\{\left. x \in \bigcup p\,\right|\,\bigcup p \neq \bigcap p \rarr x \notin \bigcap p \right\}.</math> | ||
=== प्रकार === | |||
क्रमित युग्म की उपर्युक्त कुराटोव्स्की परिभाषा "पर्याप्त" है क्योंकि यह उन चारित्रिक गुणधर्मों को संतुष्ट करती है जो क्रमित युग्म को संतुष्ट करना चाहिए, अर्थात वह <math>(a,b) = (x,y) \leftrightarrow (a=x) \land (b=y)</math>. विशेष रूप से, यह पर्याप्त रूप से 'आदेश' को व्यक्त करता है, जिसमें <math>(a,b) = (b,a)</math> तब तक गलत है जब तक कि <math>b = a</math>. समान या कम जटिलता की अन्य परिभाषाएँ हैं, जो समान रूप से पर्याप्त हैं | |||
* <math>( a, b )_{\text{reverse}} := \{ \{ b \}, \{a, b\}\};</math> | * <math>( a, b )_{\text{reverse}} := \{ \{ b \}, \{a, b\}\};</math> | ||
* <math>( a, b )_{\text{short}} := \{ a, \{a, b\}\};</math> | * <math>( a, b )_{\text{short}} := \{ a, \{a, b\}\};</math> | ||
* <math>( a, b )_{\text{01}} := \{\{0, a \}, \{1, b \}\}.</math><ref>This differs from Hausdorff's definition in not requiring the two elements 0 and 1 to be distinct from ''a'' and ''b''.</ref> | * <math>( a, b )_{\text{01}} := \{\{0, a \}, \{1, b \}\}.</math><ref>This differs from Hausdorff's definition in not requiring the two elements 0 and 1 to be distinct from ''a'' and ''b''.</ref> | ||
विपरीत परिभाषा केवल कुराटोस्की परिभाषा का | विपरीत परिभाषा केवल कुराटोस्की परिभाषा का निरर्थक संस्करण है, और इस तरह कोई स्वतंत्र हित नहीं है। परिभाषा को छोटा कहा जाता है क्योंकि इसमें [[ब्रेसिज़ (विराम चिह्न)]] के तीन युग्म के बजाय दो की आवश्यकता होती है। यह साबित करने के लिए कि विशिष्ट संपत्ति को संतुष्ट करता है, नियमितता के ज़र्मेलो-फ्रेंकेल समुच्चय सिद्धांत की आवश्यकता होती है।<ref>Tourlakis, George (2003) ''Lectures in Logic and Set Theory. Vol. 2: Set Theory''. Cambridge Univ. Press. Proposition III.10.1.</ref><nowiki> इसके अलावा, यदि कोई प्राकृतिक संख्याओं के वॉन न्यूमैन के प्राकृतिक संख्याओं के समुच्चय-सैद्धांतिक निर्माण का उपयोग करता है, तो 2 को समुच्चय {0, 1} = {0, {0}} के रूप में परिभाषित किया जाता है, जो युग्म (0, 0)</nowiki><sub>लघु</sub> से अप्रभेद्य है। फिर भी छोटी युग्म का एक और नुकसान यह तथ्य है कि भले ही ''a'' और ''b'' एक ही प्रकार के हों, छोटी युग्म के तत्व नहीं हैं। (हालांकि, यदि ''a'' = ''b'' तो लघु संस्करण में कार्डिनलिटी 2 बनी रहती है, जो कि किसी भी "युग्म" से उम्मीद की जा सकती है, जिसमें "क्रमित युग्म" भी शामिल है। | ||
==== सिद्ध करना कि परिभाषाएँ विशेषता गुण को संतुष्ट करती हैं ==== | ==== सिद्ध करना कि परिभाषाएँ विशेषता गुण को संतुष्ट करती हैं ==== | ||
सिद्ध होना: (a, b) = (c, d) [[अगर और केवल अगर]] a = c और b = d। | |||
==== '''कुराटोव्स्की''' ==== | |||
<nowiki>यदि a = c और b = d, तो {{</nowiki>''a''}, {''a, b''<nowiki>}} = {{</nowiki>''c''}, {''c, d''<nowiki>}}. इस प्रकार (a, b)</nowiki><sub>K</sub> = (c, d)<sub>K</sub>. | |||
केवल दो मामले a = b, और a ≠ b। | |||
अगर a = b | |||
:(a, b)<sub>K</sub><nowiki> = {{</nowiki>''a''}, {''a, b''<nowiki>}} = {{</nowiki>''a''}, {''a, a''<nowiki>}} = </nowiki><nowiki>{{</nowiki>''a''<nowiki>}}.</nowiki> | |||
:<nowiki>{{</nowiki>''c''}, {''c, d''<nowiki>}} = (c, d)</nowiki><sub>K</sub> = (a, b)<sub>K</sub> = <nowiki>{{</nowiki>''a''<nowiki>}}.</nowiki> | |||
: इस प्रकार {c} = {c, d} = {a}, जिसका अर्थ है a = c और a = d प्रमेय से, a = b अत b = d। | |||
यदि a ≠ b, तो (a, b)<sub>K</sub> = (c, d)<sub>K</sub><nowiki> तात्पर्य {{</nowiki>''a''}, {''a, b''<nowiki>}} = {{</nowiki>''c''}, {''c, d''<nowiki>}}.</nowiki> | |||
: <nowiki>मान लीजिए {c, d} = {a}। तब c = d = a, और इसलिए {{</nowiki>''c''}, {''c, d''<nowiki>}} = {{</nowiki>''a''}, {''a, a''<nowiki>}} = {{</nowiki>''a''}, {''a''<nowiki>}} = </nowiki><nowiki>{{</nowiki>''a''<nowiki>}}. परन्तु फिर {{</nowiki>''a''}, {''a, b''<nowiki>}} भी बराबर होगा {{</nowiki>''a''<nowiki>}}, कि b = a जो a ≠ b के विपरीत हो।</nowiki> | |||
:मान लीजिए {c} = {a, b}, तब a = b = c, जो a ≠ b का भी विरोध करता है। | |||
:इसलिए {c} = {a}, ताकि c = a और {c, d} = {a, b} हो। | |||
:यदि d = a सत्य थे, तो {c, d} = {a, a} = {a} ≠ {a, b}, एक विरोधाभास इस प्रकार d = b स्थिति है, ताकि a = c और b = d हो। | |||
==== ''''प्रतिलोम'''<nowiki/>' ==== | |||
(''a, b'')<sub>रिवर्स</sub><nowiki> = {{</nowiki>''b''}, {''a, b''<nowiki>}} = {{</nowiki>''b''}, {''b, a''<nowiki>}} = (</nowiki>''b, a'')<sub>K</sub>. | |||
''If''. If (''a, b'')<sub>रिवर्स</sub> = (''c, d'')<sub>रिवर्स</sub>, (''b, a'')<sub>K</sub> = (''d, c'')<sub>K</sub> इसलिए, ''b = d'' और ''a = c''. | |||
''यदि'' ''a = c'' और ''b = d''<nowiki>, तो {{</nowiki>''b''}, {''a, b''<nowiki>}} = {{</nowiki>''d''}, {''c, d''<nowiki>}} इस प्रकार (</nowiki>''a, b'')<sub>रिवर्स</sub> = (''c, d'')<sub>रिवर्स</sub>. | |||
'''संक्षेप में''' | |||
' | यदि ''a = c'' और ''b = d'', तो {''a'', {''a, b''<nowiki>}} = {</nowiki>''c'', {''c, d''<nowiki>}} इस प्रकार (</nowiki>''a, b'')<sub>छोटा</sub> = (''c, d'')<sub>छोटा</sub>. | ||
''केवल यदि'' मान लीजिए {''a'', {''a, b''<nowiki>}} = {</nowiki>''c'', {''c, d''<nowiki>}}. तब a बाएँ हाथ की ओर है, और इस प्रकार दाएँ हाथ में है। क्योंकि समान समुच्चय में समान अवयव होते हैं, a = c या a = {c, d} में से कोई एक स्थिति होना चाहिए</nowiki> | |||
: यदि ''a'' = { ''c, d'' }, तो उपरोक्त के समान तर्क से, { ''a, b'' } दाहिने हाथ की ओर है, इसलिए { ''a, b'' } = ''c'' या { ''a, b'' } = { ''c, d'' }। | |||
:: यदि { ''a, b'' } = ''c'' तो ''c'' { ''c, d'' } = ''a'' में है और ''a'' ''c'' में है, और यह संयोजन नियमितता के सिद्धांत के विपरीत है, क्योंकि { ''a, c'' } के संबंध में "तत्व" के तहत कोई न्यूनतम तत्व नहीं है। | |||
:: यदि { ''a, b'' } = { ''c, d'' }, तो ''a'' = { ''c, d'' } = { ''a'' '', b'' } से ''a'' का एक अवयव है, फिर से नियमितता का विरोध करता है। इसलिए ''a = c'' धारण करना चाहिए | |||
दोबारा, हम देखते हैं कि { ''a, b'' } = ''c'' या { ''a, b'' } = { ''c, d'' }। | |||
:विकल्प { ''a, b'' } = ''c'' और ''a = c'' का अर्थ है कि ''c'', ''c'' का एक तत्व है, जो नियमितता का विरोध करता है। | |||
:तो हमारे पास ''a = c'' और { ''a, b'' } = { ''c, d'' }, और इसलिए { ''b'' } = { ''a, b'' } \ { ''a'' } = { ''c, d'' } \ { ''c'' } = { ''d'' }, तो ''b'' = d । | |||
: | |||
=== कुइन–रोसेर का परिभाषा === | |||
: | [[:hi:जे। बार्कले रोसेर|रोसेर]] (1953) <ref>[[J. Barkley Rosser]], 1953. ''Logic for Mathematicians''. McGraw–Hill.</ref> ने [[:hi:विलार्ड वैन ऑरमन क्वीन|कुइन]] के कारण आदेशित युग्म की परिभाषा को नियोजित किया जिसके लिए [[:hi:प्राकृतिक संख्या|प्राकृतिक संख्याओं]] की पूर्व परिभाषा की आवश्यकता होती है। मान लीजिए कि <math>\N</math> प्राकृतिक संख्याओं का समुच्चय है और पहले परिभाषित करें | ||
: | |||
<math>\sigma(x) := \begin{cases} | |||
x, & \text{if }x \not\in \N, \\ | x, & \text{if }x \not\in \N, \\ | ||
x+1, & \text{if }x \in \N. | x+1, & \text{if }x \in \N. | ||
\end{cases}</math> | \end{cases}</math> | ||
कार्यात्मक अपने तर्क को बढ़ाता है यदि यह एक प्राकृतिक संख्या है और इसे अन्यथा छोड़ देता है संख्या 0 के कार्यात्मक मान के σ रूप में प्रकट नहीं होती है। जैसा <math> {\displaystyle x\smallsetminus \mathbb {N} }{\displaystyle x\smallsetminus \mathbb {N} } </math> के तत्वों का समूह है जो <math>\N</math> में नहीं चलने वाले तत्वों का समूह है | |||
:<math>\varphi(x) := \sigma[x] = \{\sigma(\alpha)\mid\alpha \in x\} = (x \smallsetminus \N) \cup \{n+1 : n \in (x \cap \N) \}.</math> | |||
यह | : <math>\varphi(x) := \sigma[x] = \{\sigma(\alpha)\mid\alpha \in x\} = (x \smallsetminus \N) \cup \{n+1 : n \in (x \cap \N) \}.</math> | ||
:<math>\varphi(x) \neq \{0\} \cup \varphi(y).</math> | :यह σ के तहत समुच्चय x की समुच्चय इमेज है, जिसे कभी-कभी σ″ x द्वारा भी दर्शाया जाता है। आवेदन समारोह φ समुच्चय x में इसमें प्रत्येक प्राकृतिक संख्या में वृद्धि होती है। विशेष रूप से, φ(एक्स) में कभी भी 0 नहीं होता है, ताकि किसी भी समुच्चय x और y के लिए, | ||
: <math>\varphi(x) \neq \{0\} \cup \varphi(y).</math> | |||
आगे परिभाषित करें | आगे परिभाषित करें | ||
अंत में, | <math>\psi(x) := \sigma[x] \cup \{0\} = \varphi(x) \cup \{0\}.</math> | ||
(जो | इसके द्वारा, x में हमेशा संख्या 0 होती है। | ||
अंत में, क्रमित युग्म (A, B) को अलग संघ के रूप में परिभाषित किया जा सकता है | |||
<math>(A, B) := \varphi[A] \cup \psi[B] = \{\varphi(a) : a \in A\} \cup \{\varphi(b) \cup \{0\} : b \in B \}.</math> | |||
(जो वैकल्पिक <math>\varphi''A \cup \psi''B</math> संकेतन में है)। | |||
युग्म के सभी तत्वों को निकालना जिसमें 0 नहीं है और φ को पूर्ववत करने से A मिलता है। इसी तरह युग्म के उन तत्वों से B को पुनर्प्राप्त किया जा सकता है जिनमें 0 होता है। | |||
उदाहरण के लिए <math>( \{\{a,0\},\{b,c,1\}\} , \{\{d,2\},\{e,f,3\}\} )</math>, युग्म को दिए गए <math>\{\{a,1\},\{b,c,2\},\{d,3,0\},\{e,f,4,0\}\}</math> के अनुसार एन्कोड <math>a,b,c,d,e,f\notin \N</math> किया गया है। | |||
उदाहरण के लिए | |||
प्रकार के सिद्धांत में और उसके परिणाम में जैसे स्वयंसिद्ध समुच्चय सिद्धांत एनएफ, कुइन-रॉसर युग्म के अनुमानों के समान प्रकार है और इसलिए इसे "प्रकार-स्तर" में क्रमित की गई युग्म कहा जाता है। इसलिए इस परिभाषा में क्रमित युग्म के समुच्चय के रूप में परिभाषित फ़ंक्शन को सक्षम करने का लाभ है, इसके तर्कों के प्रकार से केवल 1 प्रकार अधिक है। यह परिभाषा तभी काम करती है जब प्राकृतिक संख्याओं का समुच्चय अनंत हो। एनएफ में यह मामला है, लेकिन प्रकार सिद्धांत या एनएफयू में नहीं। जे बार्कले रोसेर ने दिखाया कि इस तरह के प्रकार-स्तरीय क्रमित युग्म (या यहां तक कि "प्रकार-स्तर द्वारा 1" क्रमित युग्म) का अस्तित्व अनंत के स्वयंसिद्ध का अर्थ है। क्विनियन समुच्चय सिद्धांतों के संदर्भ में क्रमित युग्म की व्यापक चर्चा के लिए, होम्स (1998) देखें। | |||
=== कैंटर-फ्रीज परिभाषा === | |||
समुच्चय सिद्धांत के विकास की प्रारम्भ में, विरोधाभासों की खोज से पहले, कैंटर ने दो सेटों की क्रमबद्ध जोड़ी को इन सेटों के बीच धारण करने वाले सभी संबंधों के वर्ग के रूप में परिभाषित करके फ्रीज का अनुसरण किया, यह मानते हुए कि संबंध की धारणा आदिम है | |||
<math>(x, y) = \{R : x R y \}.</math> | |||
यह परिभाषा अधिकांश आधुनिक औपचारिक समुच्चय सिद्धांतों में अस्वीकार्य है और समुच्चय के आधारभूत को परिभाषित करने के समान है, जो दिए गए समुच्चय के साथ सभी सेटों के वर्ग के रूप में है।<ref>{{cite book|last=Kanamori|first=Akihiro|url=http://math.bu.edu/people/aki/16.pdf|title=Set Theory From Cantor to Cohen|publisher=Elsevier BV|year=2007}} p. 22, footnote 59</ref> | |||
=== मोर्स परिभाषा === | === मोर्स परिभाषा === | ||
मोर्स-केली | मोर्स-केली समुच्चय सिद्धांत उचित वर्गों का मुफ्त उपयोग करता है।<ref>{{cite book|last=Morse|first=Anthony P.|url=https://archive.org/details/theoryofsets0000mors|title=A Theory of Sets|publisher=Academic Press|year=1965|url-access=registration}}</ref> मोर्स ने क्रमित युग्मो को परिभाषित किया ताकि इसके प्रक्षेपण उचित वर्ग और साथ ही समुच्चय हो सकें। (कुरातोव्स्की की परिभाषा इसकी अनुमति नहीं देती है।) उन्होंने सबसे पहले आदेशित युग्मों को परिभाषित किया जिनके प्रक्षेपण कुराटोस्की के तरीके से निर्धारित किए गए हैं। उन्होंने युग्मो को फिर से परिभाषित किया | ||
: <math> (x, y) = (\{0\} \times s(x)) \cup (\{1\} \times s(y))</math> | |||
:जहां घटक कार्टेशियन उत्पाद समुच्चय के कुराटोस्की युग्म हैं और जहां | |||
: <math> s(x) = \{\emptyset \} \cup \{\{t\} \mid t \in x\} </math> | |||
यह संभावित युग्मों को प्रस्तुत करता है जिनके प्रक्षेपण उचित वर्ग हैं। उपरोक्त क्विन-रॉसर परिभाषा भी उचित वर्गों को अनुमानों के रूप में स्वीकार करती है। इसी प्रकार, ट्रिपल को 3-ट्यूपल के रूप में परिभाषित किया गया है: | |||
<math> (x, y, z) = (\{0\} \times s(x)) \cup (\{1\} \times s(y)) \cup (\{2\} \times s(z))</math> | |||
: | : | ||
सिंगलटन समुच्चय s (x) का उपयोग जिसमें एक खाली समुच्चय डाला गया है, टुपल्स को विशिष्टता संपत्ति रखने की अनुमति देता है कि यदि ए एक एन-टुपल है और बी एक एम-ट्यूपल है और A = B फिर N = M। क्रमित त्रिक जो क्रमित युग्मों के रूप में परिभाषित हैं, उनके पास क्रमित युग्मों के संबंध में यह संपत्ति नहीं है। | |||
=== स्वयंसिद्ध परिभाषा === | === स्वयंसिद्ध परिभाषा === | ||
क्रमित युग्म को ज़र्मेलो-फ्रेंकेल समुच्चय सिद्धांत (ZF) में ऑर्डर किए गए युग्म को केवल ZF में एरिटी 2 के नए फ़ंक्शन चिह्न f (यह प्रायः छोड़ा गया है) और <math>f</math> के लिए परिभाषित स्वयंसिद्ध जोड़कर स्वयंसिद्ध रूप से प्रस्तुत किया जा सकता है | |||
<math>{\displaystyle f(a_{1},b_{1})=f(a_{2},b_{2}){\text{ if and only if }}a_{1}=a_{2}{\text{ and }}b_{1}=b_{2}.} | |||
</math> | |||
यह परिभाषा स्वीकार्य है क्योंकि ZF का यह विस्तार रूढ़िवादी विस्तार है। | |||
परिभाषा तथाकथित आकस्मिक प्रमेय जैसे (a,a) = <nowiki>{{a}}</nowiki><nowiki>, {a} ∈ (a,b) से बचने में मदद करती है, अगर कुराटोस्की की परिभाषा (a, b) = {{a}, { a, b } } प्रयोग किया गया।</nowiki> | |||
परिभाषा तथाकथित आकस्मिक | |||
== श्रेणी सिद्धांत == | == श्रेणी सिद्धांत == | ||
[[File:CategoricalProduct-03.svg|thumb| | [[File:CategoricalProduct-03.svg|thumb|समुच्चय उत्पाद X1×X2 के लिए क्रमविनिमेय आरेख।]] | ||
श्रेणी-सैद्धांतिक उत्पाद A × B समुच्चय की श्रेणी में आदेशित युग्म के समुच्चय का प्रतिनिधित्व करता है, जिसमें पहला तत्व A से आता है और दूसरा B से आता है। इस संदर्भ में ऊपर की विशेषता संपत्ति उत्पाद की सार्वभौमिक संपत्ति का परिणाम है। उत्पाद और तथ्य यह है कि समुच्चय X के तत्वों को 1 (एक तत्व समुच्चय) से X तक नियमवाद के साथ पहचाना जा सकता है। जबकि विभिन्न वस्तुओं में सार्वभौमिक संपत्ति हो सकती है, वे सभी स्वाभाविक रूप से समरूपी हैं। | |||
[[Category:Articles with short description]] | |||
[[Category:CS1 maint]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 26/11/2022]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
==संदर्भ== | ==संदर्भ== | ||
{{Reflist|30em}} | {{Reflist|30em}} | ||
| Line 213: | Line 219: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 26/11/2022]] | [[Category:Created On 26/11/2022]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 15:04, 19 October 2023

गणित में, क्रमित युग्म' (a, b) वस्तुओं का युग्म है। जिस क्रम में वस्तुएं दिखाई देती हैं वह महत्वपूर्ण है क्रमित युग्म (a, b) क्रमित युग्म (b, a) से भिन्न है जब तक' a' = 'b' न हो। (इसके विपरीत, अव्यवस्थित युग्म {a, b} अव्यवस्थित युग्म {b, a} के बराबर होती है।)
क्रमित युग्मों को 2-टुपल्स, या अनुक्रम (कभी-कभी, कंप्यूटर विज्ञान के संदर्भ में सूचियाँ) भी कहा जाता है जिनकी लंबाई 2 होती है। अदिशों के क्रमित युग्मों को कभी-कभी 2-आयामी सदिश कहा जाता है।
(तकनीकी रूप से, यह शब्दावली का अनुचित उपयोग है क्योंकि क्रमित युग्मों को सदिश स्थल का तत्व नहीं होना चाहिए।) क्रमित युग्मों की प्रविष्टियां अन्य क्रमित युग्म हो सकते हैं, जो क्रमित एन -ट्यूपल्स (n वस्तुओं की क्रमबद्ध सूचियां) की पुनरावर्ती परिभाषा को सक्षम करते हैं। उदाहरण के लिए, क्रमित ट्रिपल (a, b, c) को (a, (b,c)) के रूप में परिभाषित किया जा सकता है, अर्थात, एक युग्म दूसरे में स्थिर है।
क्रमित युग्म (a, b) में, वस्तु a को पहली प्रवेश कहा जाता है, और वस्तु b को युग्म की दूसरी प्रवेश कहलाती है। वैकल्पिक रूप से, वस्तुओं को पहले और दूसरे घटक, पहले और दूसरे निर्देशांक, या क्रमित युग्म के बाएं और दाएं अनुमान कहा जाता है।
कार्तीय गुणनफल और द्विआधारी संबंध (और इसलिए फलन) क्रमित युग्मों के रूप में परिभाषित किए गए हैं, चित्र में।
सामान्यता
माना तथा युग्मों का आदेश दिया जाए। फिर क्रमित युग्मों की विशेषता (या परिभाषित) है
सभी क्रमित युग्मों का समुच्चय (गणित) जिसकी पहली प्रविष्टि किसी समुच्चय A में है और जिसकी दूसरी प्रविष्टि किसी समुच्चय B में है, A और B का कार्तीय गुणन कहलाता है, और A × B लिखा जाता है। समुच्चय A और B के बीच एक द्विआधारी संबंध A × B का उपसमुच्चय है।
(a, b) संकेत चिन्ह का उपयोग अन्य उद्देश्यों के लिए किया जा सकता है, विशेष रूप से वास्तविक संख्या रेखा पर खुले अंतराल को दर्शाने के रूप में ऐसी स्थितियों में, संदर्भ प्रायः यह स्पष्ट कर देगा कि कौन सा अर्थ अभीष्ट है।[1][2] अतिरिक्त स्पष्टीकरण के लिए, क्रमित युग्मों को भिन्न संकेत चिन्ह द्वारा दर्शाया जा सकता है , परंतु इस संकेत चिन्ह के अन्य उपयोग भी हैं।
युग्म p के बाएँ और दाएँ प्रक्षेपण को प्रायः क्रमशः π1(p) और π2(p), या πℓ(p) और πr(p), द्वारा निरूपित किया जाता है क्रमशः ऐसे संदर्भों में जहां मनमाने ढंग से एन-टुपल्स पर विचार किया जाता है, πn
i(टी) एन-ट्यूपल टी के आई-वें घटक के लिए एक सामान्य संकेत है।
अनौपचारिक और औपचारिक परिभाषाएँ
कुछ परिचयात्मक गणित की पाठ्यपुस्तकों में क्रमबद्ध युग्म की एक अनौपचारिक (या सहज) परिभाषा दी गई है,
जैसे किन्हीं भी दो वस्तुओं के लिए a तथा b के लिए, क्रमित युग्म (a, b) उस क्रम में दो वस्तुओं a तथा b को निर्दिष्ट करने वाला संकेत चिन्ह है।[3]
इसके बाद प्रायः दो तत्वों के एक समुच्चय की तुलना की जाती है, यह संकेत करते हुए कि एक समुच्चय में a तथा b अलग होना चाहिए, लेकिन एक क्रमित युग्मों में वे समान हो सकते हैं और जबकि एक समुच्चय के तत्वों को सूचीबद्ध करने का क्रम मायने नहीं रखता है, क्रमित युग्मों में अलग-अलग प्रविष्टियों के क्रम को बदलने से क्रमित युग्म बदल जाती है।
यह "परिभाषा" असंतोषजनक है क्योंकि यह केवल वर्णनात्मक है और आदेश की सहज समझ पर आधारित है। हालांकि, जैसा कि कभी-कभी बताया गया है, इस विवरण पर भरोसा करने से कोई नुकसान नहीं होगा और लगभग हर कोई इस तरीके से क्रमित युग्मों के बारे में सोचता है।[4]
अधिक संतोषजनक दृष्टिकोण यह देखना है कि गणित में क्रमित युग्मों की भूमिका को समझने के लिए ऊपर दिए गए क्रमित युग्मों के चारित्रिक गुणों की आवश्यकता है। इसलिए क्रमित युग्म को एक आदिम धारणा के रूप में लिया जा सकता है, जिसका संबद्ध अभिगृहीत अभिलाक्षणिक गुण है। यह निकोलस बॉरबाकी द्वारा लिया गया दृष्टिकोण था। यह 1954 में प्रकाशित अपने समुच्चय का सिद्धांत में एन.बॉरबाकी समूह द्वारा लिया गया। हालांकि, इस दृष्टिकोण में इसकी कमियां भी हैं क्योंकि क्रमित युग्मों के अस्तित्व और उनकी विशिष्ट संपत्ति दोनों को स्वयंसिद्ध रूप से ग्रहण किया जाना चाहिए।[3]
क्रमित युग्मों से सख्ती से व्यवहार का एक और तरीका उन्हें समुच्चय सिद्धांत के संदर्भ में औपचारिक रूप से परिभाषित करना है। यह कई तरीकों से किया जा सकता है और इसका लाभ यह है कि समुच्चय सिद्धांत को परिभाषित करने वाले स्वयंसिद्धों से अस्तित्व और विशिष्ट संपत्ति को सिद्ध किया जा सकता है। इस परिभाषा के सबसे उद्धृत संस्करणों में से एक कुराटोव्स्की (नीचे देखें) के कारण है और उनकी परिभाषा का उपयोग 1970 में प्रकाशित बॉरबाकी के थ्योरी ऑफ़ सेट्स के दूसरे संस्करण में किया गया था। यहां तक कि उन गणितीय पाठ्यपुस्तकों में भी जो क्रमित युग्मों की अनौपचारिक परिभाषा देती हैं अभ्यास में कुराटोस्की की औपचारिक परिभाषा का उल्लेख कीजिए।
समुच्चय सिद्धान्त का उपयोग करते हुए क्रमित युग्म को परिभाषित करना
यदि कोई इस बात से सहमत है कि समुच्चय सिद्धांत गणित की एक आकर्षक नींव है, तो सभी गणितीय वस्तुओं को किसी प्रकार के समुच्चय (गणित) के रूप में परिभाषित किया जाना चाहिए। इसलिए यदि क्रमित युग्म प्राथमिक के रूप में नहीं लिया जाता है, तो इसे समुच्चय के रूप में परिभाषित किया जाना चाहिए।[5] क्रमित युग्मों की कई समुच्चय-सैद्धांतिक परिभाषाएँ नीचे दी गई हैं (यह भी देखें [6]).
वीनर की परिभाषा
नॉर्बर्ट वीनर ने 1914 में क्रमित युग्मों की पहली समुच्चय सैद्धांतिक परिभाषा प्रस्तावित की[7]
उन्होंने देखा कि इस परिभाषा ने गणितीय सिद्धांत के प्रकार सिद्धांत को समुच्चय के रूप में परिभाषित करना संभव बना दिया। गणितीय सिद्धांत ने आदिम धारणा के रूप में , और इसलिए सभी अर्थों का संबंध लिया था।
वीनर ने प्रकार सिद्धांत के साथ परिभाषा को संगत बनाने के लिए {b} के बजाय {{b}} का इस्तेमाल किया, जहां वर्ग में सभी तत्व समान "प्रकार" के होने चाहिए। एक अतिरिक्त समुच्चय के भीतर नेस्टेड, b के साथ,इसका प्रकार 's के बराबर है।
हॉसडॉर्फ की परिभाषा
लगभग उसी समय वीनर (1914) के रूप में, फेलिक्स हॉसडॉर्फ ने अपनी परिभाषा प्रस्तावित की
"जहाँ 1 और 2 दो अलग-अलग वस्तुएँ हैं जो a और b से भिन्न हैं।[8]
कुराटोस्की की परिभाषा
1921 में काज़िमिर्ज़ कुराटोव्स्की ने क्रमित युग्मों (a, b) अब स्वीकृत परिभाषा की पेशकश की[9][10]
ध्यान दें कि इस परिभाषा का उपयोग तब भी किया जाता है जब पहले और दूसरे निर्देशांक समान हों
कुछ क्रमित युग्म p को देखते हुए, गुण "x, p का पहला निर्देशांक है", इस प्रकार तैयार किया जा सकता है
संपत्ति "x p का दूसरा निर्देशांक है" जिसे इस प्रकार तैयार किया जा सकता है
इस मामले में बाएँ और दाएँ निर्देशांक समान हैं, दाएँ संयोजन
निरर्थक रूप से सत्य है, क्योंकि Y1 ≠ Y2 ऐसा कभी नहीं होता।
यह है कि हम एक युग्म के पहले समन्वय को कैसे निकाल सकते हैं (एकपक्षीय प्रतिच्छेदन और एकपक्षीय मिलन के लिए पुनरावृत्त-संचालन संकेत चिन्ह का उपयोग करके)
इस प्रकार दूसरा निर्देशांक निकाला जा सकता है
प्रकार
क्रमित युग्म की उपर्युक्त कुराटोव्स्की परिभाषा "पर्याप्त" है क्योंकि यह उन चारित्रिक गुणधर्मों को संतुष्ट करती है जो क्रमित युग्म को संतुष्ट करना चाहिए, अर्थात वह . विशेष रूप से, यह पर्याप्त रूप से 'आदेश' को व्यक्त करता है, जिसमें तब तक गलत है जब तक कि . समान या कम जटिलता की अन्य परिभाषाएँ हैं, जो समान रूप से पर्याप्त हैं
विपरीत परिभाषा केवल कुराटोस्की परिभाषा का निरर्थक संस्करण है, और इस तरह कोई स्वतंत्र हित नहीं है। परिभाषा को छोटा कहा जाता है क्योंकि इसमें ब्रेसिज़ (विराम चिह्न) के तीन युग्म के बजाय दो की आवश्यकता होती है। यह साबित करने के लिए कि विशिष्ट संपत्ति को संतुष्ट करता है, नियमितता के ज़र्मेलो-फ्रेंकेल समुच्चय सिद्धांत की आवश्यकता होती है।[12] इसके अलावा, यदि कोई प्राकृतिक संख्याओं के वॉन न्यूमैन के प्राकृतिक संख्याओं के समुच्चय-सैद्धांतिक निर्माण का उपयोग करता है, तो 2 को समुच्चय {0, 1} = {0, {0}} के रूप में परिभाषित किया जाता है, जो युग्म (0, 0)लघु से अप्रभेद्य है। फिर भी छोटी युग्म का एक और नुकसान यह तथ्य है कि भले ही a और b एक ही प्रकार के हों, छोटी युग्म के तत्व नहीं हैं। (हालांकि, यदि a = b तो लघु संस्करण में कार्डिनलिटी 2 बनी रहती है, जो कि किसी भी "युग्म" से उम्मीद की जा सकती है, जिसमें "क्रमित युग्म" भी शामिल है।
सिद्ध करना कि परिभाषाएँ विशेषता गुण को संतुष्ट करती हैं
सिद्ध होना: (a, b) = (c, d) अगर और केवल अगर a = c और b = d।
कुराटोव्स्की
यदि a = c और b = d, तो {{a}, {a, b}} = {{c}, {c, d}}. इस प्रकार (a, b)K = (c, d)K.
केवल दो मामले a = b, और a ≠ b।
अगर a = b
- (a, b)K = {{a}, {a, b}} = {{a}, {a, a}} = {{a}}.
- {{c}, {c, d}} = (c, d)K = (a, b)K = {{a}}.
- इस प्रकार {c} = {c, d} = {a}, जिसका अर्थ है a = c और a = d प्रमेय से, a = b अत b = d।
यदि a ≠ b, तो (a, b)K = (c, d)K तात्पर्य {{a}, {a, b}} = {{c}, {c, d}}.
- मान लीजिए {c, d} = {a}। तब c = d = a, और इसलिए {{c}, {c, d}} = {{a}, {a, a}} = {{a}, {a}} = {{a}}. परन्तु फिर {{a}, {a, b}} भी बराबर होगा {{a}}, कि b = a जो a ≠ b के विपरीत हो।
- मान लीजिए {c} = {a, b}, तब a = b = c, जो a ≠ b का भी विरोध करता है।
- इसलिए {c} = {a}, ताकि c = a और {c, d} = {a, b} हो।
- यदि d = a सत्य थे, तो {c, d} = {a, a} = {a} ≠ {a, b}, एक विरोधाभास इस प्रकार d = b स्थिति है, ताकि a = c और b = d हो।
'प्रतिलोम'
(a, b)रिवर्स = {{b}, {a, b}} = {{b}, {b, a}} = (b, a)K.
If. If (a, b)रिवर्स = (c, d)रिवर्स, (b, a)K = (d, c)K इसलिए, b = d और a = c.
यदि a = c और b = d, तो {{b}, {a, b}} = {{d}, {c, d}} इस प्रकार (a, b)रिवर्स = (c, d)रिवर्स.
संक्षेप में
यदि a = c और b = d, तो {a, {a, b}} = {c, {c, d}} इस प्रकार (a, b)छोटा = (c, d)छोटा.
केवल यदि मान लीजिए {a, {a, b}} = {c, {c, d}}. तब a बाएँ हाथ की ओर है, और इस प्रकार दाएँ हाथ में है। क्योंकि समान समुच्चय में समान अवयव होते हैं, a = c या a = {c, d} में से कोई एक स्थिति होना चाहिए
- यदि a = { c, d }, तो उपरोक्त के समान तर्क से, { a, b } दाहिने हाथ की ओर है, इसलिए { a, b } = c या { a, b } = { c, d }।
- यदि { a, b } = c तो c { c, d } = a में है और a c में है, और यह संयोजन नियमितता के सिद्धांत के विपरीत है, क्योंकि { a, c } के संबंध में "तत्व" के तहत कोई न्यूनतम तत्व नहीं है।
- यदि { a, b } = { c, d }, तो a = { c, d } = { a , b } से a का एक अवयव है, फिर से नियमितता का विरोध करता है। इसलिए a = c धारण करना चाहिए
दोबारा, हम देखते हैं कि { a, b } = c या { a, b } = { c, d }।
- विकल्प { a, b } = c और a = c का अर्थ है कि c, c का एक तत्व है, जो नियमितता का विरोध करता है।
- तो हमारे पास a = c और { a, b } = { c, d }, और इसलिए { b } = { a, b } \ { a } = { c, d } \ { c } = { d }, तो b = d ।
कुइन–रोसेर का परिभाषा
रोसेर (1953) [13] ने कुइन के कारण आदेशित युग्म की परिभाषा को नियोजित किया जिसके लिए प्राकृतिक संख्याओं की पूर्व परिभाषा की आवश्यकता होती है। मान लीजिए कि प्राकृतिक संख्याओं का समुच्चय है और पहले परिभाषित करें
कार्यात्मक अपने तर्क को बढ़ाता है यदि यह एक प्राकृतिक संख्या है और इसे अन्यथा छोड़ देता है संख्या 0 के कार्यात्मक मान के σ रूप में प्रकट नहीं होती है। जैसा के तत्वों का समूह है जो में नहीं चलने वाले तत्वों का समूह है
- यह σ के तहत समुच्चय x की समुच्चय इमेज है, जिसे कभी-कभी σ″ x द्वारा भी दर्शाया जाता है। आवेदन समारोह φ समुच्चय x में इसमें प्रत्येक प्राकृतिक संख्या में वृद्धि होती है। विशेष रूप से, φ(एक्स) में कभी भी 0 नहीं होता है, ताकि किसी भी समुच्चय x और y के लिए,
आगे परिभाषित करें
इसके द्वारा, x में हमेशा संख्या 0 होती है।
अंत में, क्रमित युग्म (A, B) को अलग संघ के रूप में परिभाषित किया जा सकता है
(जो वैकल्पिक संकेतन में है)।
युग्म के सभी तत्वों को निकालना जिसमें 0 नहीं है और φ को पूर्ववत करने से A मिलता है। इसी तरह युग्म के उन तत्वों से B को पुनर्प्राप्त किया जा सकता है जिनमें 0 होता है।
उदाहरण के लिए , युग्म को दिए गए के अनुसार एन्कोड किया गया है।
प्रकार के सिद्धांत में और उसके परिणाम में जैसे स्वयंसिद्ध समुच्चय सिद्धांत एनएफ, कुइन-रॉसर युग्म के अनुमानों के समान प्रकार है और इसलिए इसे "प्रकार-स्तर" में क्रमित की गई युग्म कहा जाता है। इसलिए इस परिभाषा में क्रमित युग्म के समुच्चय के रूप में परिभाषित फ़ंक्शन को सक्षम करने का लाभ है, इसके तर्कों के प्रकार से केवल 1 प्रकार अधिक है। यह परिभाषा तभी काम करती है जब प्राकृतिक संख्याओं का समुच्चय अनंत हो। एनएफ में यह मामला है, लेकिन प्रकार सिद्धांत या एनएफयू में नहीं। जे बार्कले रोसेर ने दिखाया कि इस तरह के प्रकार-स्तरीय क्रमित युग्म (या यहां तक कि "प्रकार-स्तर द्वारा 1" क्रमित युग्म) का अस्तित्व अनंत के स्वयंसिद्ध का अर्थ है। क्विनियन समुच्चय सिद्धांतों के संदर्भ में क्रमित युग्म की व्यापक चर्चा के लिए, होम्स (1998) देखें।
कैंटर-फ्रीज परिभाषा
समुच्चय सिद्धांत के विकास की प्रारम्भ में, विरोधाभासों की खोज से पहले, कैंटर ने दो सेटों की क्रमबद्ध जोड़ी को इन सेटों के बीच धारण करने वाले सभी संबंधों के वर्ग के रूप में परिभाषित करके फ्रीज का अनुसरण किया, यह मानते हुए कि संबंध की धारणा आदिम है
यह परिभाषा अधिकांश आधुनिक औपचारिक समुच्चय सिद्धांतों में अस्वीकार्य है और समुच्चय के आधारभूत को परिभाषित करने के समान है, जो दिए गए समुच्चय के साथ सभी सेटों के वर्ग के रूप में है।[14]
मोर्स परिभाषा
मोर्स-केली समुच्चय सिद्धांत उचित वर्गों का मुफ्त उपयोग करता है।[15] मोर्स ने क्रमित युग्मो को परिभाषित किया ताकि इसके प्रक्षेपण उचित वर्ग और साथ ही समुच्चय हो सकें। (कुरातोव्स्की की परिभाषा इसकी अनुमति नहीं देती है।) उन्होंने सबसे पहले आदेशित युग्मों को परिभाषित किया जिनके प्रक्षेपण कुराटोस्की के तरीके से निर्धारित किए गए हैं। उन्होंने युग्मो को फिर से परिभाषित किया
- जहां घटक कार्टेशियन उत्पाद समुच्चय के कुराटोस्की युग्म हैं और जहां
यह संभावित युग्मों को प्रस्तुत करता है जिनके प्रक्षेपण उचित वर्ग हैं। उपरोक्त क्विन-रॉसर परिभाषा भी उचित वर्गों को अनुमानों के रूप में स्वीकार करती है। इसी प्रकार, ट्रिपल को 3-ट्यूपल के रूप में परिभाषित किया गया है:
सिंगलटन समुच्चय s (x) का उपयोग जिसमें एक खाली समुच्चय डाला गया है, टुपल्स को विशिष्टता संपत्ति रखने की अनुमति देता है कि यदि ए एक एन-टुपल है और बी एक एम-ट्यूपल है और A = B फिर N = M। क्रमित त्रिक जो क्रमित युग्मों के रूप में परिभाषित हैं, उनके पास क्रमित युग्मों के संबंध में यह संपत्ति नहीं है।
स्वयंसिद्ध परिभाषा
क्रमित युग्म को ज़र्मेलो-फ्रेंकेल समुच्चय सिद्धांत (ZF) में ऑर्डर किए गए युग्म को केवल ZF में एरिटी 2 के नए फ़ंक्शन चिह्न f (यह प्रायः छोड़ा गया है) और के लिए परिभाषित स्वयंसिद्ध जोड़कर स्वयंसिद्ध रूप से प्रस्तुत किया जा सकता है
यह परिभाषा स्वीकार्य है क्योंकि ZF का यह विस्तार रूढ़िवादी विस्तार है।
परिभाषा तथाकथित आकस्मिक प्रमेय जैसे (a,a) = {{a}}, {a} ∈ (a,b) से बचने में मदद करती है, अगर कुराटोस्की की परिभाषा (a, b) = {{a}, { a, b } } प्रयोग किया गया।
श्रेणी सिद्धांत
श्रेणी-सैद्धांतिक उत्पाद A × B समुच्चय की श्रेणी में आदेशित युग्म के समुच्चय का प्रतिनिधित्व करता है, जिसमें पहला तत्व A से आता है और दूसरा B से आता है। इस संदर्भ में ऊपर की विशेषता संपत्ति उत्पाद की सार्वभौमिक संपत्ति का परिणाम है। उत्पाद और तथ्य यह है कि समुच्चय X के तत्वों को 1 (एक तत्व समुच्चय) से X तक नियमवाद के साथ पहचाना जा सकता है। जबकि विभिन्न वस्तुओं में सार्वभौमिक संपत्ति हो सकती है, वे सभी स्वाभाविक रूप से समरूपी हैं।
संदर्भ
- ↑ Lay, Steven R. (2005), Analysis / With an Introduction to Proof (4th ed.), Pearson / Prentice Hall, p. 50, ISBN 978-0-13-148101-5
- ↑ Devlin, Keith (2004), Sets, Functions and Logic / An Introduction to Abstract Mathematics (3rd ed.), Chapman & Hall / CRC, p. 79, ISBN 978-1-58488-449-1
- ↑ 3.0 3.1 Wolf, Robert S. (1998), Proof, Logic, and Conjecture / The Mathematician's Toolbox, W. H. Freeman and Co., p. 164, ISBN 978-0-7167-3050-7
- ↑ Fletcher, Peter; Patty, C. Wayne (1988), Foundations of Higher Mathematics, PWS-Kent, p. 80, ISBN 0-87150-164-3
- ↑ Quine has argued that the set-theoretical implementations of the concept of the ordered pair is a paradigm for the clarification of philosophical ideas (see "Word and Object", section 53). The general notion of such definitions or implementations are discussed in Thomas Forster "Reasoning about theoretical entities".
- ↑ Dipert, Randall. "क्रमबद्ध जोड़े के सेट-सैद्धांतिक प्रतिनिधित्व और संबंधों के तर्क के लिए उनकी पर्याप्तता।".
{{cite web}}: CS1 maint: url-status (link) - ↑ Wiener's paper "A Simplification of the logic of relations" is reprinted, together with a valuable commentary on pages 224ff in van Heijenoort, Jean (1967), From Frege to Gödel: A Source Book in Mathematical Logic, 1979–1931, Harvard University Press, Cambridge MA, ISBN 0-674-32449-8 (pbk.). van Heijenoort states the simplification this way: "By giving a definition of the ordered pair of two elements in terms of class operations, the note reduced the theory of relations to that of classes".
- ↑ cf introduction to Wiener's paper in van Heijenoort 1967:224
- ↑ cf introduction to Wiener's paper in van Heijenoort 1967:224. van Heijenoort observes that the resulting set that represents the ordered pair "has a type higher by 2 than the elements (when they are of the same type)"; he offers references that show how, under certain circumstances, the type can be reduced to 1 or 0.
- ↑ Kuratowski, Casimir (1921). "सेट थ्योरी में आदेश की धारणा पर" (PDF). Fundamenta Mathematicae. 2 (1): 161–171. doi:10.4064/fm-2-1-161-171. Archived from the original (PDF) on 2019-04-29. Retrieved 2013-05-29.
- ↑ This differs from Hausdorff's definition in not requiring the two elements 0 and 1 to be distinct from a and b.
- ↑ Tourlakis, George (2003) Lectures in Logic and Set Theory. Vol. 2: Set Theory. Cambridge Univ. Press. Proposition III.10.1.
- ↑ J. Barkley Rosser, 1953. Logic for Mathematicians. McGraw–Hill.
- ↑ Kanamori, Akihiro (2007). Set Theory From Cantor to Cohen (PDF). Elsevier BV. p. 22, footnote 59
- ↑ Morse, Anthony P. (1965). A Theory of Sets. Academic Press.
- Templates that generate short descriptions
- Collapse templates
- Created On 26/11/2022
- Machine Translated Page
- Navigational boxes
- Navigational boxes without horizontal lists
- Sidebars with styles needing conversion
- Templates generating microformats
- Templates that are not mobile friendly
- Wikipedia metatemplates
- Mathematics navigational boxes
- Navbox orphans
- Philosophy and thinking navigational boxes
- Templates Translated in Hindi
- समुच्चय सिद्धांत में मूलभूत अवधारणा
- आदेश सिद्धांत
- प्ररूप सिद्धांत
- Vigyan Ready