अनंत सेट

From alpha
Jump to navigation Jump to search
Set Theory Image
सिद्धांत छवि सेट करें

समुच्चय सिद्धांत में, एक अनंत समुच्चय एक समुच्चय (गणित) है जो परिमित समुच्चय नहीं है। अनन्त सेट गणनीय सेट या बेशुमार सेट हो सकते हैं।[1][2]


गुण

प्राकृतिक संख्या ओं का समुच्चय (जिसका अस्तित्व अनंत के स्वयंसिद्ध द्वारा माना जाता है) अनंत है।[2][3] यह एकमात्र ऐसा समुच्चय है जो स्वयंसिद्ध ों द्वारा अनंत होने के लिए प्रत्यक्ष रूप से आवश्यक है। ज़र्मेलो-फ्रेंकेल सबसेट थ्योरी (ZFC) में किसी भी अन्य अनंत सेट के अस्तित्व को साबित किया जा सकता है, लेकिन केवल यह दिखा कर कि यह प्राकृतिक संख्याओं के अस्तित्व से अनुसरण करता है।

एक सेट अनंत है अगर और केवल अगर प्रत्येक प्राकृतिक संख्या के लिए, सेट में एक उपसमुच्चय है जिसकी प्रमुखता वह प्राकृतिक संख्या है।[citation needed] यदि पसंद का स्वयंसिद्ध धारण करता है, तो एक सेट अनंत है अगर और केवल अगर इसमें एक गणनीय अनंत उपसमुच्चय शामिल है।

यदि सेट का एक सेट अनंत है या इसमें एक अनंत तत्व है, तो इसका मिलन अनंत है। अनंत समुच्चय का घात समुच्चय अनंत होता है।[4]अनंत समुच्चय का कोई भी उपसमुच्चय अनंत होता है। यदि एक अपर िमित समुच्चय को परिमित रूप से अनेक उपसमुच्चयों में विभाजित किया जाता है, तो उनमें से कम से कम एक अपरिमित होना चाहिए। कोई भी सेट जिसे अनंत सेट पर मैप किया जा सकता है वह अनंत है। अनंत समुच्चय और अरिक्त समुच्चय का कार्तीय गुणन फल अनंत होता है। सेट की असीमित संख्या का कार्टेशियन उत्पाद, प्रत्येक में कम से कम दो तत्व होते हैं, या तो खाली या अनंत होता है; यदि पसंद का स्वयंसिद्ध धारण करता है, तो यह अनंत है।

यदि एक अनंत समुच्चय एक सुव्यवस्थित समुच्चय है, तो इसमें एक गैर-खाली, गैर-तुच्छ उपसमुच्चय होना चाहिए जिसमें कोई सबसे बड़ा तत्व न हो।

ZF में, एक सेट अनंत है अगर और केवल अगर इसके सत्ता स्थापित का पावर सेट एक डेडेकिंड-अनंत सेट है, जिसके पास एक उचित उपसमुच्चय समतुल्य है।[5] यदि पसंद का अभिगृहीत भी सत्य है, तो अनंत समुच्चय निश्चित रूप से डेडेकाइंड-अनंत समुच्चय हैं।

यदि एक अनंत समुच्चय एक सुक्रमित समुच्चय है, तो इसके कई सुव्यवस्थित समुच्चय होते हैं जो गैर-समरूपी होते हैं।

अनंत समुच्चय सिद्धांत में प्रमाण और परिभाषाएँ शामिल हैं।[6] बर्टन द्वारा चर्चा किए गए महत्वपूर्ण विचारों में शामिल हैं कि सेट के तत्वों या भागों को कैसे परिभाषित किया जाए, सेट में अद्वितीय तत्वों को कैसे परिभाषित किया जाए और अनंतता को कैसे सिद्ध किया जाए।[6]बर्टन विभिन्न प्रकार की अनंतता के प्रमाणों पर भी चर्चा करता है, जिसमें गणनीय और बेशुमार सेट शामिल हैं।[6] अनंत और परिमित सेटों की तुलना करते समय उपयोग किए जाने वाले विषयों में ऑर्डर किए गए सेट, कार्डिनैलिटी, समतुल्यता, समन्वय विमान, सार्वभौमिक सेट, मैपिंग, सबसेट, निरंतरता और पारगमन शामिल हैं।[6] कैंडर के निर्धारित विचार त्रिकोणमिति और अपरिमेय संख्याओं से प्रभावित थे। बर्टन, पाउला, नारली और रॉजर द्वारा वर्णित अनंत सेट सिद्धांत में अन्य प्रमुख विचारों में वास्तविक संख्याएं शामिल हैं जैसे पाई, पूर्णांक और यूलर की संख्या।[6][7][8] बर्टन और रोजर्स दोनों ही प्रूफ कॉन्सेप्ट्स जैसे मैपिंग, प्रूफ बाय इंडक्शन या प्रूफ बाय कॉन्ट्रैक्शन का इस्तेमाल करके अनंत सेट की व्याख्या शुरू करने के लिए परिमित सेट का उपयोग करते हैं।[6][8]अनंत समुच्चयों को समझने के लिए गणितीय वृक्षों का भी उपयोग किया जा सकता है।[9] बर्टन अनंत सेटों के प्रमाणों पर भी चर्चा करता है जिसमें यूनियनों और सबसेट जैसे विचार शामिल हैं।[6] गणित का इतिहास: एक परिचय के अध्याय 12 में, बर्टन ने जोर दिया कि कैसे गणितज्ञों जैसे ज़र्मेलो, डेडेकिंड, गैलीलियो, क्रोनकर, कैंटर और बोलजानो ने अनंत सेट सिद्धांत की जांच की और प्रभावित किया।[6] संभावित ऐतिहासिक प्रभाव, जैसे कि 1800 के दशक में प्रशिया के इतिहास के परिणामस्वरूप विद्वानों के गणितीय ज्ञान में वृद्धि हुई, जिसमें कैंडर का अनंत सेट का सिद्धांत भी शामिल था।[6] ज़र्मेलो, डेडेकिंड, गैलीलियो, क्रोनकर, कैंटर और बोलजानो सहित गणितज्ञों ने अनंत सेट सिद्धांत की जांच की या प्रभावित किया। इनमें से कई गणितज्ञों ने या तो अनंतता पर बहस की या अन्यथा अनंत सेटों के विचारों में जोड़ा।[6]

अनंत समुच्चय सिद्धांत का एक संभावित अनुप्रयोग आनुवंशिकी और जीव विज्ञान में है।[10]


उदाहरण

अनगिनत अनंत सेट

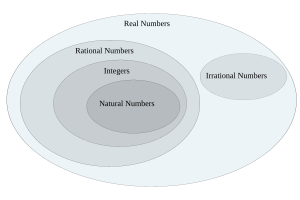
सभी पूर्णांक ों का समुच्चय, {..., -1, 0, 1, 2, ...} एक गणनीय अनंत समुच्चय है। सभी सम पूर्णांकों का समुच्चय भी एक गणनीय रूप से अनंत समुच्चय होता है, भले ही वह पूर्णांकों का उचित उपसमुच्चय हो।[4] सभी परिमेय संख्याओं का समुच्चय एक अनगिनत अनंत समुच्चय है क्योंकि पूर्णांकों के समुच्चय में आपत्ति है।[4]


बेशुमार अनंत सेट

सभी वास्तविक संख्या ओं का समुच्चय एक बेशुमार अनंत समुच्चय है। सभी अपरिमेय संख्या ओं का समुच्चय भी एक बेशुमार अनंत समुच्चय है।[4]


यह भी देखें

संदर्भ

  1. ↑ Weisstein, Eric W. "Infinite Set". mathworld.wolfram.com. Retrieved 2019-11-29.
  2. ↑ 2.0 2.1 "infinite set in nLab". ncatlab.org. Retrieved 2019-11-29.
  3. ↑ Bagaria, Joan (2019), "Set Theory", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Fall 2019 ed.), Metaphysics Research Lab, Stanford University, retrieved 2019-11-30
  4. ↑ 4.0 4.1 4.2 4.3 Caldwell, Chris. "The Prime Glossary — Infinite". primes.utm.edu. Retrieved 2019-11-29.
  5. ↑ Boolos, George (1994), "The advantages of honest toil over theft", Mathematics and mind (Amherst, MA, 1991), Logic Comput. Philos., Oxford Univ. Press, New York, pp. 27–44, MR 1373892. See in particular pp. 32–33.
  6. ↑ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 6.7 6.8 6.9 Burton, David (2007). The History of Mathematics: An Introduction (6th ed.). Boston: McGraw Hill. pp. 666–689. ISBN 9780073051895.
  7. ↑ Pala, Ozan; Narli, Serkan (2020-12-15). "Role of the Formal Knowledge in the Formation of the Proof Image: A Case Study in the Context of Infinite Sets". Turkish Journal of Computer and Mathematics Education (TURCOMAT). 11 (3): 584–618. doi:10.16949/turkbilmat.702540. S2CID 225253469.
  8. ↑ 8.0 8.1 Rodgers, Nancy (2000). Learning to reason: an introduction to logic, sets and relations. New York: Wiley. ISBN 978-1-118-16570-6. OCLC 757394919.
  9. ↑ Gollin, J. Pascal; Kneip, Jakob (2021-04-01). "Representations of Infinite Tree Sets". Order. 38 (1): 79–96. doi:10.1007/s11083-020-09529-0. ISSN 1572-9273. S2CID 201646182.
  10. ↑ Shelah, Saharon; Strüngmann, Lutz (2021-06-01). "Infinite combinatorics in mathematical biology". Biosystems. 204: 104392. doi:10.1016/j.biosystems.2021.104392. ISSN 0303-2647. PMID 33731280. S2CID 232298447.


बाहरी कड़ियाँ

श्रेणी:प्रमुख संख्याएं

Retrieved from "https://alpha.indicwiki.in/index.php?title=अनंत_सेट&oldid=85988"